基于近場動力學的單晶冰彈性各向異性數(shù)值模擬方法1)

黃焱 王建平 孫劍橋

(天津大學水利工程仿真與安全國家重點實驗室,天津 300350)

引言

近年來,環(huán)北極與近北極國家相繼出臺了新的極地政策或戰(zhàn)略部署[1-3],極地海域的商業(yè)航運、資源開發(fā)、科學考察、環(huán)境保護及軍事保障等活動也隨之日趨白熱化.海冰是極地海域標志性的環(huán)境條件,也是極地航行船舶和極地作業(yè)裝備在安全性保障上面對的首要挑戰(zhàn).為應對這一挑戰(zhàn),學術界與工程界開展了大量關于冰-結構相互作用過程的數(shù)值模擬方法研究[4-6],以期能夠為工程裝備在現(xiàn)實冰環(huán)境條件下的承載過程提供可靠的預報.然而,天然海冰因其復雜的力學性質,致使當前的數(shù)值模擬結果直接面向工程應用時尚存在極大的阻礙.因此,如何建立可靠的冰力學性質的數(shù)值模擬方法,已成為當前學術界關注的焦點問題之一.

已有大量的研究表明,天然冰材料在變形和破壞行為上都具有顯著的各向異性特征[7-10],這一特征成為冰-結構相互作用過程中產生復雜載荷過程的關鍵誘因.因此,在數(shù)值模擬中準確再現(xiàn)冰材料這一關鍵的力學特征,就成為保障數(shù)值預報結果合理性的必要條件.基于此,一些學者探索了將天然冰材料表現(xiàn)出的整體各向異性特征引入數(shù)值模擬方法的途徑,如Castelnau 等[11]探索了一種模擬多晶冰黏塑性行為各向異性的自洽方法;Hibler 和Schulson 等[12]將缺陷導致的各向異性引入到海冰數(shù)值模型中,并據(jù)此進行了雙軸壓縮模擬,探討了模型中海冰的裂紋擴展模式;季順迎和岳前進[13]針對海冰的動力過程模擬問題,討論了彈塑性各向異性模型的適用性;文獻[14]基于原位冰芯樣本的實測數(shù)據(jù),建立了不同晶體織構下的彈性剛度張量,并將其引入冰層力學模型之中,由此計算和分析了多晶冰織構特征所導致的各向異性對冰內地震波傳播方式的影響.但正如冰力學研究領域知名學者E.M.Schulson 所言,多晶冰材料(見圖1)的各向異性特征根源于單晶冰的各向異性[15].所以,對于天然冰材料各向異性特征的模擬,首先應建立針對單晶冰各向異性的再現(xiàn)方法,由此構建出模擬天然冰材料各向異性特征的基本框架,再進一步由此框架擴展出多晶冰材料的模擬方法,才可能全面、準確地再現(xiàn)天然冰材料的特殊力學性質.本文將針對當前學術界缺乏單晶冰材料各向異性模擬方法的局面,開展探索性研究工作.

圖1 S2 冰的水平向與垂向晶體切片[15]Fig.1 Horizontal and vertical sections of S2 ice[15]

另一方面,在數(shù)值模擬方法上,基于非局部作用思想的近場動力學方法,因其在統(tǒng)一連續(xù)介質力學理論與粒子模擬方法上具有突出的潛質,已在學術界引起廣泛關注[16-19].在近場動力學模型中,物質點間的相互作用力函數(shù)(即“本構力函數(shù)”)包含了材料的物性信息,它不再以傳統(tǒng)的應力-應變關系等形式出現(xiàn),也不假設位移場的連續(xù)性,求解時不存在空間求導.此外,位移場的連續(xù)與否并不影響基本方程的求解,不連續(xù)性(如裂紋、界面)在求解運動方程時自然產生,因而不會出現(xiàn)傳統(tǒng)連續(xù)性模型求解時出現(xiàn)的病態(tài)特征[18].當前,近場動力學方法已被大量應用于巖石、復合材料裂紋萌生擴展過程的模擬[20-22],并在材料復雜力學行為特征的模擬上顯示出突出的優(yōu)勢.鑒于此,這一方法也開始被引入冰-結構相互作用問題的模擬中,并因其在冰材料斷裂破壞現(xiàn)象模擬上的良好表現(xiàn)而備受青睞[23-26].需要指出的是,目前近場動力學方法在應用于工程預報時,都還是基于簡單的各向同性材料假設,進而導致已有的模擬結果尚難以合理再現(xiàn)真實作用場景.

據(jù)此,本文在回顧單晶冰彈性各向異性力學表征的基礎上,采用近場動力學方法建立單晶冰態(tài)基模型,通過對單軸壓縮過程的數(shù)值模擬,探討彈性各向異性特征的引入方式及相關的參數(shù)標定方法,以期建立合理可靠的單晶冰彈性各向異性數(shù)值模擬方法.

1 單晶冰彈性各向異性的力學特征

在小位移條件下,應力與應變之間的關系為

其中,σi為應力分量,i,j=1,2,···,6;εi為應變分量;Sij為柔度矩陣分量.

對于單晶冰所具備的六方晶系結構,如果假設其基面內符合力學各向同性,則可分別將晶體的C軸方向及其基面內的任意一對正交方向分別定義為X3,X1和X2應力主軸,相應的柔度矩陣中只有5 個非零參數(shù)[9]

Fletcher[9]收集整理了大量的單晶冰內彈性波傳播的實驗測試數(shù)據(jù),并將這些數(shù)據(jù)回歸為描述單晶冰彈性各向異性的柔度矩陣表達,矩陣中各項系數(shù)的值分別為:S11=1040 GPa?1;S12=?430 GPa?1;S13=?240 GPa?1;S33=850 GPa?1;S44=3140 GPa?1.

進一步利用張量變換可獲得任一方向有效柔度的表達式為[9,15]

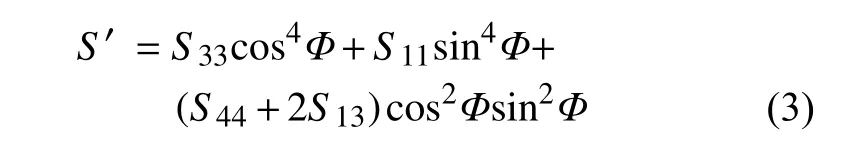
其中,Φ表示任一加載方向與C軸的夾角.而各個變形方向上的楊氏模量為該方向有效柔度的倒數(shù)

其中,Eref為參考楊氏模量.該值基于Fletcher 實驗測試獲得的單晶冰柔度矩陣系數(shù)計算得到,并將作為本文數(shù)值模型后續(xù)標定的參考值.

圖2 為由式(3)和式(4)繪制得到的單晶冰彈性各向異性特征表征圖:圖中的實線描繪的是Eref在與C軸平行的任意平面內的空間分布情況,該曲線上任意一點的橫縱坐標比值為該平面內變形方向與C軸夾角Φ的正切值,該點距離坐標原點的長度為相應方向上的楊氏模量值;圖中的虛線表征以C軸方向楊氏模量為特征值的各向同性邊界.

圖2 單晶冰彈性各向異性表征圖[9]Fig.2 Reference Young's modulus as a function of orientation[9]

由圖2 可知,楊氏模量的分布是一條關于坐標原點中心對稱和坐標軸雙對稱的閉合曲線,故對各向異性的描述可限定于第一象限內.

2 態(tài)基近場動力學模型

2.1 本構模型

在近場動力學模型的發(fā)展歷經了兩個階段,即鍵基模型和態(tài)基模型.鍵基模型的理論基礎會導致恒定泊松比的天然缺陷[18],為彌補這一理論缺陷,又進一步發(fā)展出了態(tài)基模型[27].因此,態(tài)基模型已成為當前近場動力學模型應用中的主角[28-29].下面對態(tài)基模型的基礎理論進行簡要介紹.

在態(tài)基近場動力學模型中,參考構型中x位置處材料點在t時刻的運動方程為

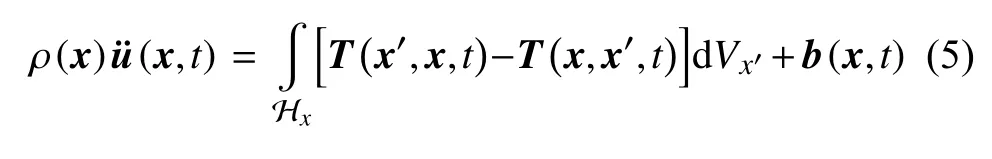
其中ρ為參考構型中材料的密度;u為位移向量場;Hx為x材料點的“近場范圍”;T(x′,x,t) 為材料點x′施加在x上的力密度向量;T(x,x′,t) 為材料點x施加在x′上的力密度向量;T(x′,x,t)?T(x,x′,t) 對應于鍵基模型中的對點力函數(shù);dVx′ 為材料點x′的體積;b為體積力向量場.

材料點x′和x之間的相互作用通過“鍵”來實現(xiàn).以ξ表示參考構型中材料點x′和x的相對位置

在t時刻的當前構型中,材料點x′和x的相對位移為

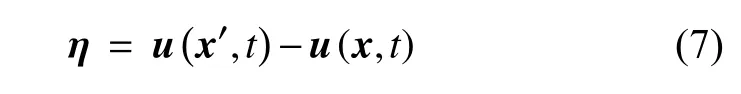
故向量 ξ +η 表示兩材料點在當前構型中的相對位置.

定義材料點x′和x之間“鍵”的伸長率為

其中,當“鍵”處于拉伸狀態(tài)時,伸長率為正;當“鍵”處于壓縮狀態(tài)時,伸長率為負.

定義材料點x處的膨脹度為

其中d為與材料無關的參數(shù).

在線性態(tài)基近場動力學固體模型中,力密度向量與當前構型中的相對位置向量 ξ +η 平行,表示為

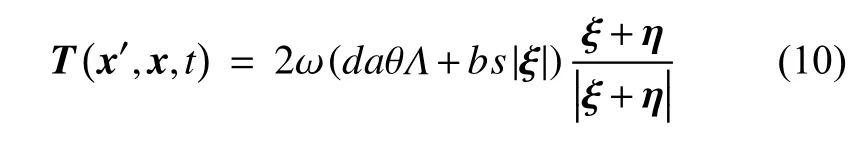
其中,ω為影響函數(shù),可根據(jù)材料點x′,x之間的距離控制它們的相互作用大小;a和b為與材料有關的參數(shù);Λ 為

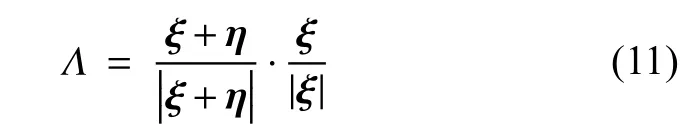
在近場動力學中,認為處于近場范圍內的材料點均會與中心材料點發(fā)生相互作用,即非局部相互作用,這是近場動力學與傳統(tǒng)連續(xù)介質力學最重要的區(qū)別之一.

文獻[30]認為,影響函數(shù)應當包含 δ 作為長度尺度的對近場范圍內其他材料點的影響,因此其提出以下影響函數(shù)

將影響函數(shù)代入式(10)可得態(tài)基近場動力學的力密度向量表達

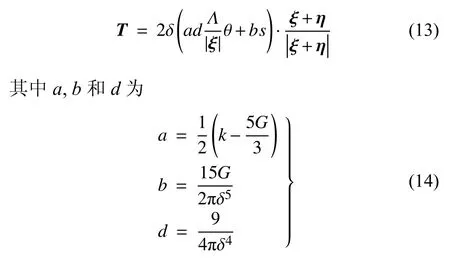
其中,k和G分別為體積模量和剪切模量,在三維情況下分別為

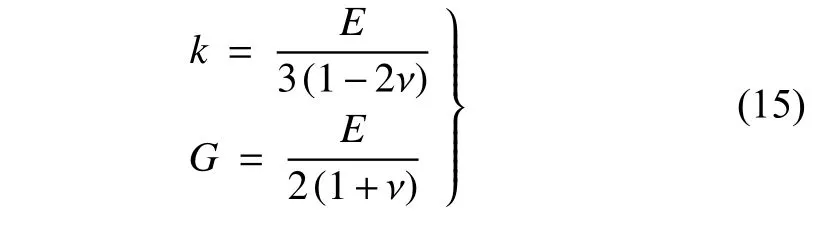
其中,E為楊氏模量;ν 為泊松比.

2.2 時間積分格式

近場動力學運動方程是一個積分-微分方程,它的解通過空間和時間的數(shù)值積分來獲得.本文采用無網格離散化方法,將材料離散為一系列具有確定體積的粒子,離散后粒子xi的運動方程變?yōu)?/p>

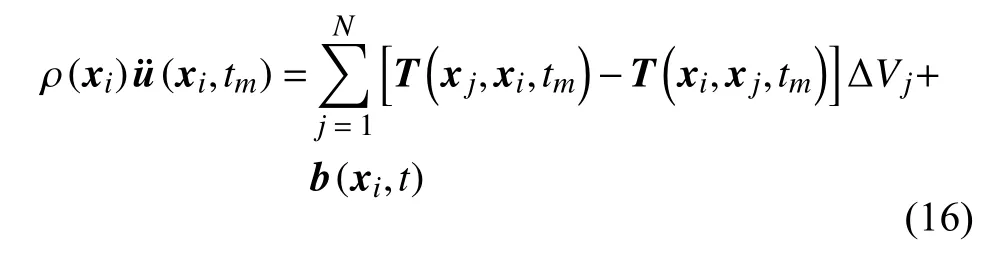
其中N為粒子xi近場范圍內的粒子數(shù),下標m表示第m個時間步.

粒子xi膨脹度θi為

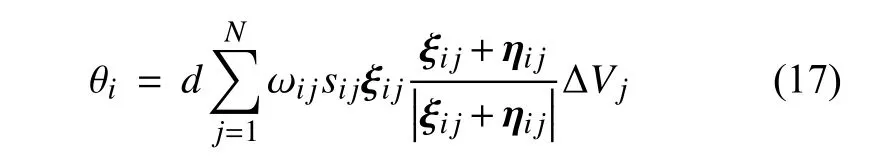
其中,下標ij代表該物理量與粒子xi和xj相關.

在獲得tm時刻的加速度后,采用以下顯式積分算法獲得下一時間步的速度和位移[30]

其中Δt為計算時間步長.

顯式積分算法雖然簡單明了,但是其只是條件穩(wěn)定的,當時間步長大于最大容許時間步長之后便不能獲得穩(wěn)定收斂解.Madenci 等利用馮·諾依曼穩(wěn)定性分析得到了臨界時間步長為[30]

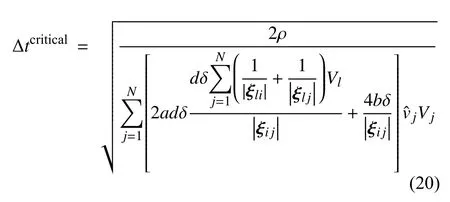
3 基于各向同性假設的單晶冰基礎態(tài)基模型

本文的近場動力學模擬借助C++程序和Visual Studio 平臺實現(xiàn),有限元模擬采用ANSYS 軟件完成.

在探究如何將各向異性引入單晶冰近場動力學模型的方法之前,首先以圖2 中展示的各向同性假設邊界為基準,對模型粒子數(shù)量(或粒子間距)取值進行標定.

如圖2 所示,各向同性假設下的楊氏模量為11.76 GPa,相應地,體積模量k=8.7 GPa;剪切模量G=4.62 GPa.

不論是天然淡水湖冰還是海冰材料,其中包含的晶粒直徑大多集中在2～ 10 mm 范圍內[31-33].據(jù)此,本文采用的單晶冰試樣模型尺寸為2.5 mm × 2.5 mm ×5.0 mm,密度為0.935 mg/mm3,如圖3 所示.

圖3 各向同性模型及載荷條件(單位:mm)Fig.3 Isotropic model and loading conditions (unit:mm)

令n為試件橫截面長度與粒子間距的比值.本文中,n分別取為8,10,16,20,25,40,此時粒子間距 ?x分別為0.3125 mm,0.25 mm,0.15625 mm,0.125 mm,0.1 mm,0.0625 mm,據(jù)此建立了6 種模型,相應的粒子數(shù)分別為1024,2000,8192,16000,31250,128000.近場范圍半徑δ取為3?x[34-36].Silling 和Askari[34]建議將邊界條件通過一個有限厚度帶狀區(qū)域內的粒子定義.本節(jié)向模型頂部和底部同時施加大小相同、方向相反的恒力壓縮載荷,大小為F=100 N,通過厚度為δ的帶狀區(qū)域內的粒子體積力定義b

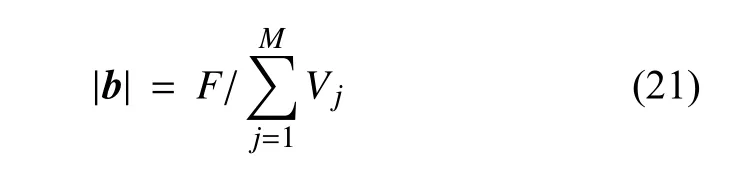
其中,M為頂部或者底部δ厚度區(qū)域內的粒子數(shù).

由于本節(jié)施加的載荷為靜力載荷,為獲得穩(wěn)定解,借助自適應動態(tài)松弛算法使模型快速達到穩(wěn)定狀態(tài)[37].同時采用商用有限元軟件ANSYS 建立相同尺度和力學性質的有限元模型,施加相同載荷,并進行靜力分析.提取近場動力學模型中位于Z軸上的所有粒子的Z向位移,與有限元計算結果進行對比,得到結果如圖4 所示.

從圖4 可以看出,當本模型中n從25 增加到40后,計算結果與有限元結果的差異均在2%以內,然而計算量卻增加了近6 倍.因此,本文將 ?x=L/25作為離散粒子間距,可以滿足計算精度和效率需求.

圖4 各粒子間距模型中心軸Z 向位移與有限元結果的對比Fig.4 Displacement variation along the loading direction

4 各向異性特征的引入方式與參數(shù)標定

在近場動力學理論中,要體現(xiàn)材料的彈性各向異性,需要從力密度的本構關系入手.在力密度向量的表達式(10)中,括號中含參數(shù)a的第一項表示體積膨脹度對力密度的貢獻,含參數(shù)b的第二項可表示體積膨脹度以外的變形對力密度的貢獻.本文認為,材料的彈性各向異性行為受體積變形和其他變形的綜合影響,因此本文提出了基于影響函數(shù)ω的各向異性模型.

4.1 基于影響函數(shù)的彈性各向異性模型

Silling 等[27]在提出態(tài)基近場動力學理論時定義影響函數(shù) ω 為:一個位于中心材料點近場范圍內的嚴格為正的標量值函數(shù).若影響函數(shù)僅與“鍵”長有關,即表示為,則影響函數(shù)為球形.目前,大量研究工作都是基于球形的影響函數(shù)[30,38-39],所表征的僅為材料的各向同性.Silling 等[27]指出,對于不規(guī)則形狀邊界的結構體或者混合物表面的模擬,可以通過定義形狀不同的影響函數(shù)來實現(xiàn).本文即遵循這一思路,擬通過定義合適的影響函數(shù),以期使模型呈現(xiàn)出各向異性特征.

在一般的態(tài)基近場動力學理論中,力密度如式(10)所示.本文初步假定材料的各向異性完全由影響函數(shù)ωij控制,模型中的其他部分與各向同性材料相同,并且各向同性部分的材料參數(shù)以單晶冰C軸方向的力學屬性為基準.

由于在各向同性理論中,力密度中的模量參數(shù)均與楊氏模量成正相關,因此,假設在各向異性模型中,各模量參數(shù)和楊氏模量具有相同的關于角度的表達,即力密度向量為

式(23)中的分母項可視為單晶冰楊氏模量隨加載方向變化的歸一化表征,由式(3)和式(4)得到;φ為模型中“鍵”與C軸的夾角.

模型約束端的總反力由所有與被約束粒子相關的力密度集體貢獻,表示為

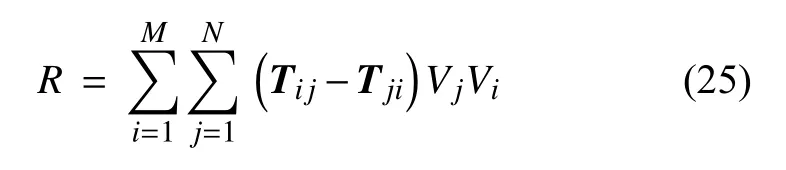
其中,R為總反力;M為被約束的粒子xi的數(shù)量;N為粒子xi近場范圍內的粒子數(shù).

在一般單軸壓縮試驗中,名義應力定義為兩端反力與構件橫截面積的比值,應變定義為構件標距段的伸長量與標距的比值,即

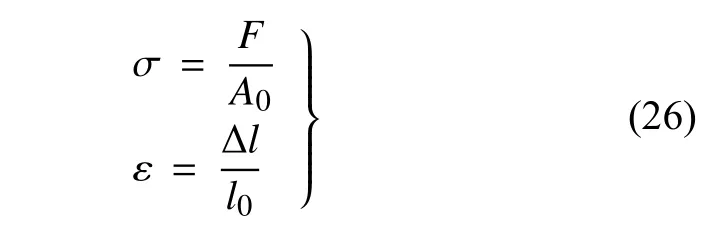
其中,F為反力;A0為構件變形前的橫截面面積;?l為標距段的伸長量;l0為標距.

類似地,定義近場動力學模型在單軸壓縮模擬中的名義應力為底部反力R與變形前橫截面面積的比值;標距為頂部虛粒子層底部與底部虛粒子層頂部之間的距離;名義應變?yōu)闃司喽蔚纳扉L量與標距的比值.結構如圖5 所示.模型尺寸與第3 節(jié)中的基礎模型相同,C軸始終位于XZ平面內.頂部的應變率載荷通過設置三層虛粒子向下的速度為應變率與試樣高度的乘積來施加,底部固定約束通過剛性固定三層虛粒子的位置來施加.本文中應變率大小均為10 s?1.

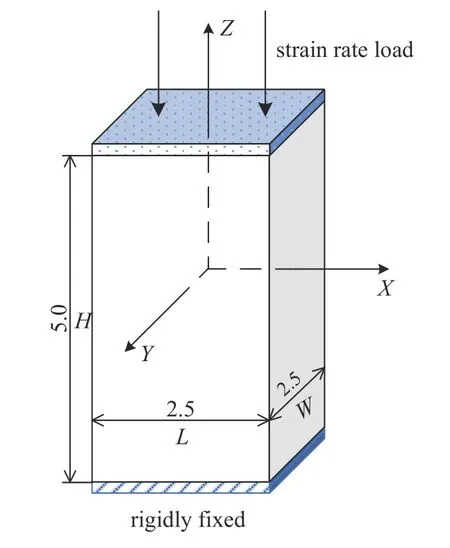
圖5 恒定應變率加載模型(單位:mm)Fig.5 Constant strain rate loading model (unit:mm)

在單晶冰中,C軸和垂直于C軸方向的力學屬性是非常重要的兩個屬性;同時,單晶冰的楊氏模量在加載方向與C軸呈45°附近時最小,因此這三個方向的楊氏模量將是本文考慮的重點.在載荷沿Z方向加載的前提下,本文通過在XZ平面內順時針旋轉C軸的角度,實現(xiàn)C軸與加載方向夾角Φ的調節(jié).采用式(23)的影響函數(shù)進行Φ=0°,45°,90°三個不同方向上的恒定應變率壓縮變形模擬,得到名義應力隨名義應變的變化關系.這三個加載方向的名義應力-名義應變關系如圖6 所示.

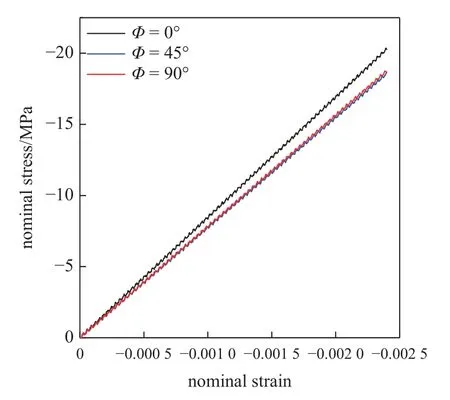
圖6 名義應力-名義應變曲線Fig.6 Nominal stress-nominal strain curve

對于線彈性模型,名義應力-名義應變曲線近似為直線,其斜率為楊氏模量.采用最小二乘法對該斜率進行擬合,即可得到數(shù)值模型的楊氏模量.在式(23)的影響函數(shù)下,三個加載方向的楊氏模量分別為:E0=8.461 GPa,E45=7.805 GPa,E90=7.877 GPa;下標數(shù)字表示加載方向與C軸方向的夾角.

觀察模擬結果并將其與圖2 的參考楊氏模量進行對比可以發(fā)現(xiàn),盡管將楊氏模量與角度的關系直接代入影響函數(shù)中,能夠使數(shù)值模型呈現(xiàn)一定程度的各向異性,但其結果與實驗測試得到的參考楊氏模量存在較大差異,仍需對該影響函數(shù)進行修正.

4.2 影響函數(shù)修正方案一:引入輔助參數(shù)α

如前所述,影響函數(shù)雖然初步繼承了楊氏模量隨加載方向變化的力學表征關系,但計算結果與參考楊氏模量仍存在數(shù)量上的差異,尤其是沿C軸加載方向.據(jù)此,本文初步推斷,若使模型能夠模擬出單晶冰沿各個加載方向的楊氏模量,需要在影響函數(shù)中加入輔助參數(shù)α的控制

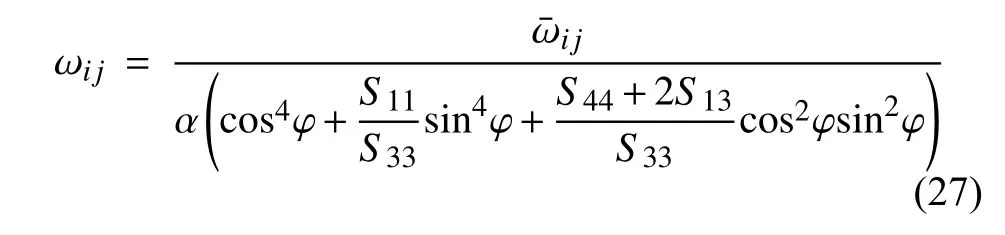
式中α可從整體水平上調節(jié)影響函數(shù)的值.式(23)可視為式(27)在α=1 時的特殊情況.此時的影響函數(shù)存在以下關系

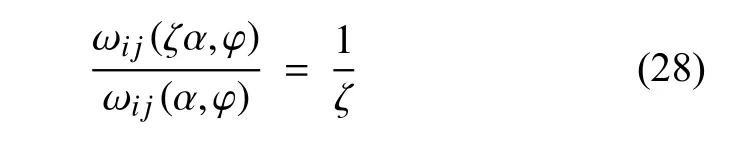
式(28)表示當任意一根“鍵”ξij的影響函數(shù)中的α變?yōu)樵瓉淼摩票逗?影響函數(shù)的值變?yōu)樵瓉淼?/ζ倍,在相同變形下,力密度也變?yōu)樵瓉淼?/ζ倍.根據(jù)式(25),反力也變?yōu)樵瓉淼?/ζ倍,則楊氏模量也應變?yōu)樵瓉淼?/ζ.

考慮到C軸方向的特殊性,首先調整α使沿C軸方向的楊氏模量與參考楊氏模量匹配.根據(jù)上一節(jié)計算得到的C軸方向的楊氏模量E0=8.461 GPa,令=0.7195.將該α控制下的影響函數(shù)代入數(shù)值模型,進行0°,45°和90°三個方向的加載模擬,最終得到該三個方向的楊氏模量分別為:E0=11.84 GPa,E45=10.81 GPa,E90=10.94 GPa.

將上述楊氏模量計算結果分別與α=1 時的計算結果進行對比,可以得到三個方向楊氏模量的比值分別為:0.7146,0.7220 和0.7200.這些比值與α=0.7195 非常接近,表明前述楊氏模量隨α增大而減小的推斷成立.

然而,盡管在α=0.7195 時沿C軸方向的數(shù)值模型楊氏模量與參考楊氏模量非常接近,但在另外兩個方向的差異較大.進一步,繪制α=1 與α=0.7195下各加載方向的楊氏模量計算結果,并與參考楊氏模量進行對比,如圖7 所示.可以發(fā)現(xiàn),數(shù)值模型楊氏模量隨加載方向變化的曲線形狀在兩種α值下幾乎沒有變化,即模型的各向異性程度沒有得到改善.因此,仍需進一步修正影響函數(shù)中的角度控制參量.

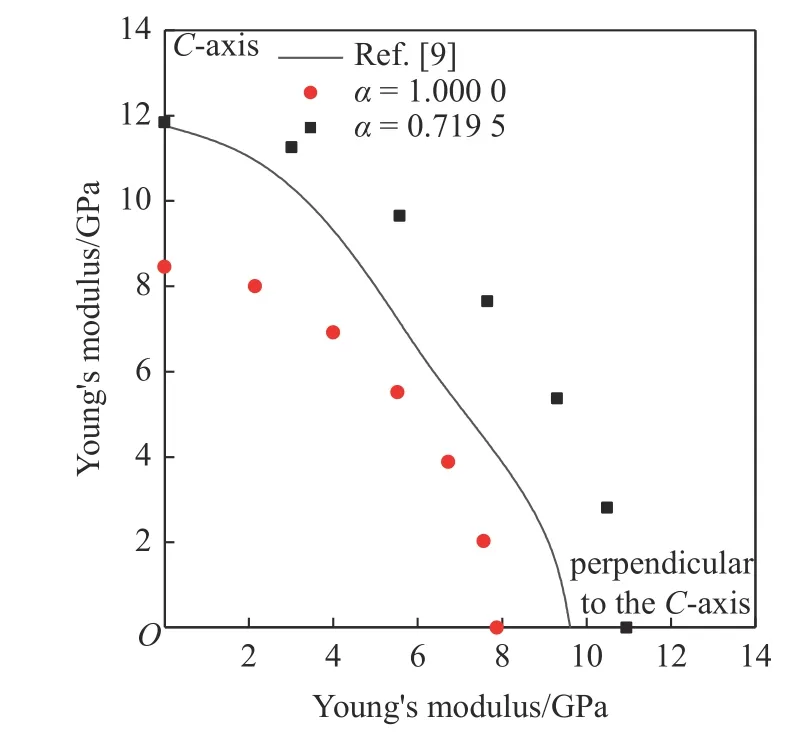
圖7 兩種不同α 時的楊氏模量對比Fig.7 Comparison of Young's modulus for two different α

4.3 影響函數(shù)修正方案二:引入輔助參數(shù)α,β,γ

修正方案一的計算結果表明,僅通過單一的輔助控制參數(shù)并不能調整模型的各向異性程度.因此本文進一步推斷,雖然影響函數(shù)與楊氏模量具有相似的關于角度的函數(shù)表達,但表達式中的各個分項的系數(shù)并不一定相同.據(jù)此,進一步假定影響函數(shù)形式為

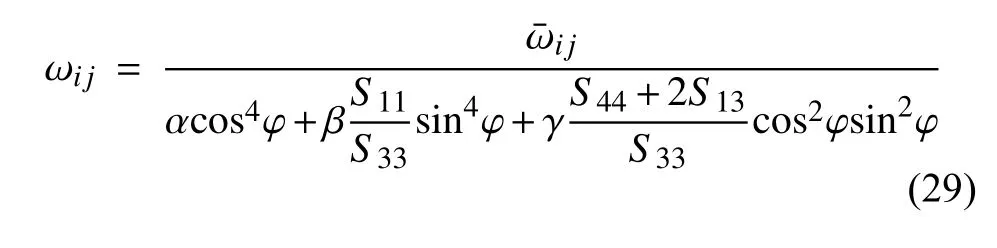
其中,α,β,γ為獨立變化的三個輔助控制參數(shù).

將該影響函數(shù)代入力密度的公式,分別令φ=0°,45°和90°,得到沿這三個方向的力密度為

由式(30)可知,沿C軸方向“鍵”的力密度主要受α的控制,垂直于C軸方向主要受β的控制,其他方向將受到三個參數(shù)的綜合影響.由于S44≥S11>S33,故與C軸呈45°夾角的“鍵”受γ影響最大.基于加載方向附近的“鍵”對該方向楊氏模量影響更大的思想,本文提出以下關于α,β,γ標定方法,上標(l)表示第l次標定

(1)l=0,令α(0),β(0),γ(0)的初始值均為0.7195,針對0°,45°,90°三個加載方向上的楊氏模量容許誤差為Δ(本文設定為0.05%);

(2) 以α(l),β(l),γ(l)建立相應的近場動力學模型,進行三個方向的恒應變率單軸壓縮數(shù)值模擬,分別得到對應的楊氏模量;

(3) 定義第l步時的總相對誤差為

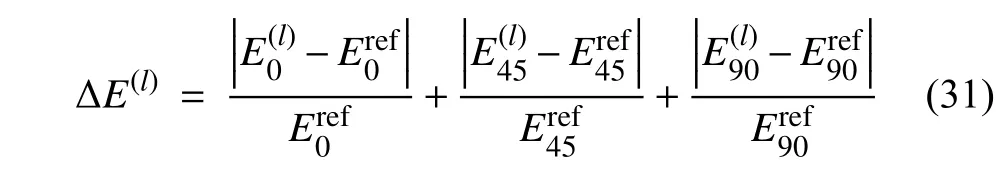
計算此時的總相對誤差 ?E(l);

(4) 若 ?E(l)≤?,輸出α,β,γ的最終值為α(l),β(l),γ(l),反之,令

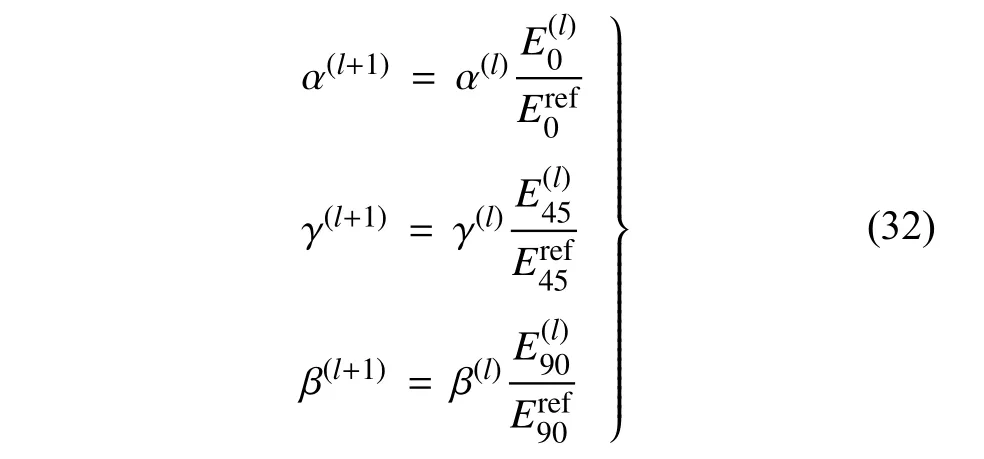
(5) 令l=l+1,重復第 (2)～ (4)步.

將α(0)=β(0)=γ(0)=0.7195 作為第一次循環(huán)的起始條件輸入,執(zhí)行上述標定過程.圖8 展示了α,β,γ值以及三個方向上楊氏模量的相對誤差隨迭代次數(shù)的變化.可以看出,隨著迭代次數(shù)的增加,α,β,γ分別穩(wěn)定收斂于不同的值,同時三個方向的相對誤差隨著迭代次數(shù)的增加而下降,這表明本文提出的迭代標定方法基本有效.此外,總誤差也隨著迭代次數(shù)的增加迅速下降,如圖9 所示.經過22 次循環(huán)后,總誤差小于設定的容許誤差Δ,此時α(22)=0.5364,β(22)=0.7506,γ(22)=1.2425,與此相對應的三個方向楊氏模量的計算結果分別為:E0=11.76 GPa,E45=8.793 GPa,E90=9.614 GPa.

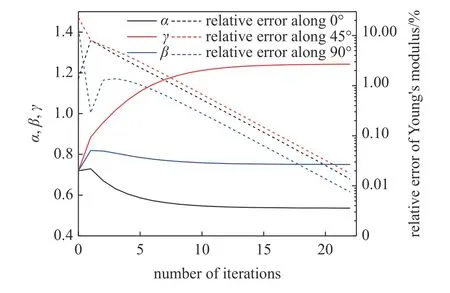
圖8 α,β,γ 及三個方向楊氏模量的相對誤差隨著迭代次數(shù)的變化Fig.8 α,β,γ and the relative error of Young's modulus as a function of iteration number

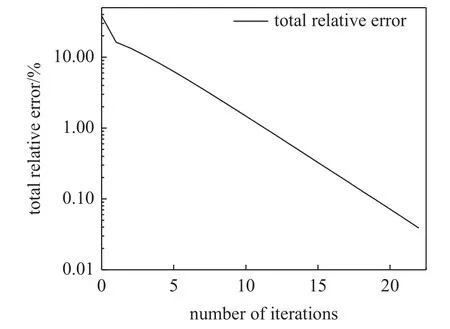
圖9 總誤差隨著迭代次數(shù)的變化Fig.9 Total error as a function of iteration number

4.4 其他加載方向的適用性驗證

影響函數(shù)修正方案二能夠較為準確地模擬沿0°,45°和90°三個加載方向的彈性變形.進一步,對其他加載方向模擬結果的準確性開展驗證.

將第22 次循環(huán)時的α,β,γ值作為終值,計算在此終值下與C軸方向分別呈15°,30°,60°和75°的四個加載方向的楊氏模量,及其與參考楊氏模量的相對誤差,如表1 所示.圖10 從曲線形狀上展示了數(shù)值模型得到的楊氏模量與參考楊氏模量的對比.

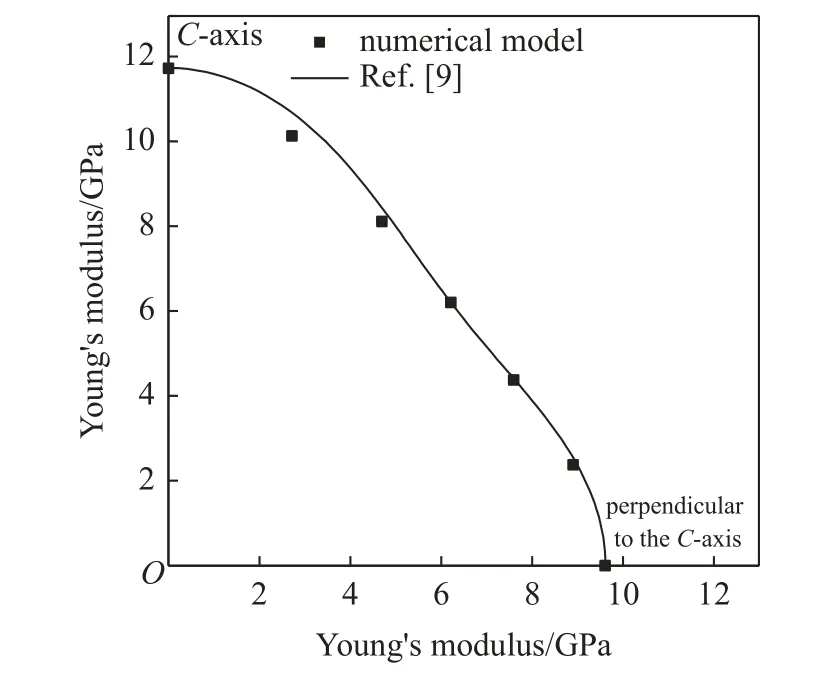
圖10 楊氏模量隨加載方向的變化趨勢對比Fig.10 Graphic comparison of Young's modulus under different loading directions

從表1 可以看出,其他四個加載方向的數(shù)值模型楊氏模量與參考楊氏模量的相對誤差均位于5%以下,處于可接受的誤差范圍內.同時,數(shù)值模型楊氏模量隨加載方向的變化趨勢與參考楊氏模量較為契合.這進一步驗證了,本文提出的基于影響函數(shù)的彈性各向異性近場動力學模型,能夠實現(xiàn)單晶冰彈性各向異性力學表征的有效模擬.

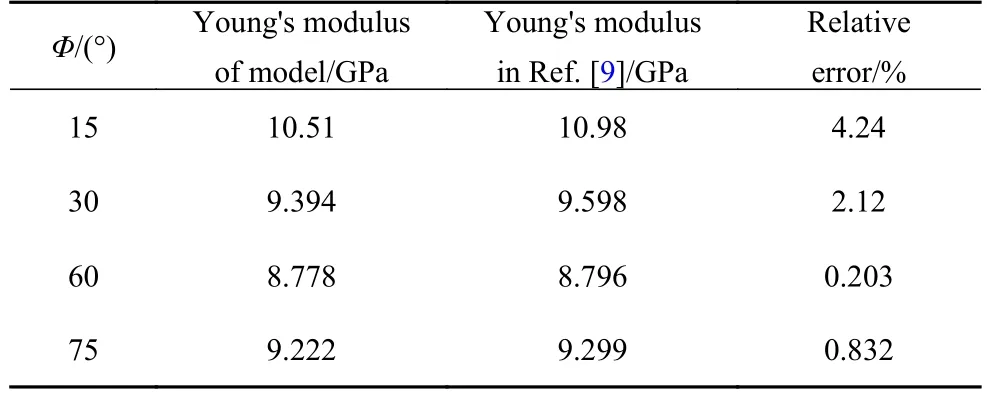
表1 四個加載方向的楊氏模量計算結果及其相對誤差Table 1 Young's modulus of the numerical model under different loading directions and the relative error

5 結論

本文基于態(tài)基近場動力學理論,根據(jù)單晶冰楊氏模量沿不同加載方向的變化規(guī)律,推斷粒子間“鍵”的變形與力密度也存在類似的規(guī)律,提出了一種從影響函數(shù)出發(fā)的彈性各向異性模型.以前人實驗測試得到的楊氏模量值為參考,通過開展與C軸呈0°,45°和90°三個加載方向的單晶冰單軸壓縮數(shù)值模擬,提出了針對該影響函數(shù)的修正和輔助參數(shù)標定方法,并且最終在15°,30°,60°和75°等其他四個加載方向進行了驗證.

計算結果表明,本文所提出的針對影響函數(shù)的修正與參數(shù)標定方法,能夠較為便捷地找到數(shù)值模型楊氏模量與參考楊氏模量相一致的影響函數(shù)最優(yōu)解,即本文提出的基于影響函數(shù)的近場動力學數(shù)值模擬方法,能夠合理、準確地模擬單晶冰的彈性各向異性行為.

值得補充的是,極地海洋工程中常見的天然冰具有典型的多晶結構,其力學行為與晶體的排列方式、晶粒尺寸等有著密不可分的聯(lián)系.同時,多晶冰的變形及裂紋成核與擴展模式不僅與單晶冰的變形有關,還受到晶界滑移等晶間作用機制的影響與控制.因此,在后續(xù)探索多晶冰的數(shù)值模擬方法時,仍需在單晶冰模擬的基礎上,重點關注晶體織構的建模、單晶之間力的傳遞過程、斷裂準則的引入等,以實現(xiàn)多晶冰變形與破壞各向異性的有效模擬.