基于信號分解和切比雪夫多項式的多體系統區間不確定性分析方法1)

蔣 鑫 白爭鋒,?,2) 寧志遠 王思宇

* (哈爾濱工業大學航天工程系,哈爾濱 150001)

? (哈爾濱工業大學(威海)機械工程系,山東威海 264209)

引言

多體系統動力學建模與仿真對機械產品系統設計及控制具有重要的理論意義和實際應用價值[1].實際工程應用中,由于加工誤差、材料屬性、邊界條件和外界激勵等因素的影響,多體系統參數呈現不確定性的變化[2-4].研究表明在系統數學模型中忽略參數的不確定性可能會導致分析結果失去參考價值[5],如2016 年斯基亞帕雷利號(Schiaparelli)火星著陸器由于忽略了降落傘展開過程中不確定因素對系統動力學的影響,導致著陸失敗[6-7].因此,開展參數不確定性對多體系統動力學特性影響規律的研究具有重要意義.

在多體系統動力學建模中,通常將不確定參數分為隨機變量和區間變量[8].隨機變量的分布信息由概率分布函數確定,基于蒙特卡洛方法,或多項混沌展開,可得到系統的響應統計特征[8-9],然而隨機參數的樣本分布信息難以獲得[10].相比而言,區間分析方法采用區間變量描述參數的不確定性,只需要獲得區間變量的上下邊界即可,因此應用范圍更廣[11].

針對含區間參數的多體機械系統,掃描法[12]作為一種簡單可靠的方法,能夠獲得系統響應的準確邊界,然而該方法的計算成本隨區間參數數目的增多而指數增長.基于泰勒展開,Wu 等[10]利用泰勒模型法研究了含區間參數多體系統的響應分析.由于基于泰勒展開的方法難以處理大不確定度問題,子區間技術將原區間劃分為多個子區間以提高計算精度[13].為避免泰勒展開方法中的求導運算,Wu 等[10]基于切比雪夫多項式,提出了切比雪夫區間方法(Chebyshev interval method,CIM),隨后該方法應用于多體系統的不確定響應分析[14-18].CIM 通過切比雪夫多項式在每個時刻近似輸出響應與輸入區間參數的關系,可以看作為基于代理模型的方法(surrogate based method,SBM)的一種.SBM 方法致力于構建計算成本低的代理模型,然后通過掃描法或者優化方法從代理模型獲得輸出響應的邊界[19].基于此理念,Feng 等[11]將Legendre 多項式應用于汽車懸架系統的區間動力學響應分析,Wang 和Yang 等[3]采用任意混沌多項式研究了大炮動力系統的區間響應.此外,徑向基函數[20]和克里金模型[21]也應用于區間不確定分析.陳光宋等[22]采用極大熵法獲得多體系統輸出參數的統計信息,進一步對分布函數采用泰勒展開獲得響應區間.

然而,基于代理模型的不確定分析方法在處理長周期的區間動力學響應問題時,隨著時間增大,得到的響應邊界會出現惡化問題.而這種現象在概率方法和區間方法中都會出現[23-24].在多體系統中,當不確定參數取不同的值時,得到的系統響應也具有不同的頻率和相位.在與時間相關的不確定動力學響應分析中,隨著時間的增大,不同樣本響應之間的相位差會逐漸增大,導致瞬時相位差累積效應(instantaneous phase difference accumulation,IPDA),從而使得系統響應與不確定性參數之間的關系也變得越來越復雜[24].由于這一原因,使得無論代理模型的階數取多高,都無法在后期時刻準確近似響應函數與不確定參數的關系,從而使得隨著時間的增大,得到的上下邊界與實際邊界存在偏差,出現邊界惡化.為此,Cui 等[24]首次將自適應信號分解技術引入基于響應面法的不確定分析中,提出RS-HHT 和RS-LMD 方法,相比于傳統的響應面法,該方法能夠采用低階多項式處理長時域區間不確定動力學響應問題.

在CIM 方法中,隨著時間增大,樣本響應間的相位差也會越來越大,此時邊界的精度會隨著時間的增大而降低,出現邊界惡化的現象(從下文分析中可以看出).為改進CIM 方法應對長時間區間不確定分析中出現的邊界惡化現象,本文將信號分解技術與切比雪夫多項式結合,采用切比雪夫多項式分別對HHT 變換(Hilbert-Huang transform,HHT)和局域均值分解(local mean decomposition,LMD)得到的瞬時幅值和瞬時相位近似,提出CIM-HHT 方法和CIM-LMD 方法.該方法將動力學響應分解為多個具有各自振幅和相位的單分量和一個殘差分量,基于切比雪夫多項式對每個單組分響應和殘差分量構建相應的代理模型,并得到系統的耦合代理模型.最后,以典型的單擺和曲柄滑塊機構為例,考慮模型中的參數不確定性,驗證了CIM-HHT 和CIM-LMD 方法的有效性.

1 多體系統的切比雪夫區間方法

1.1 含區間參數的多體系統動力學建模

通常,不考慮參數的不確定性時,多體系統的動力學特性可由一組微分代數方程描述

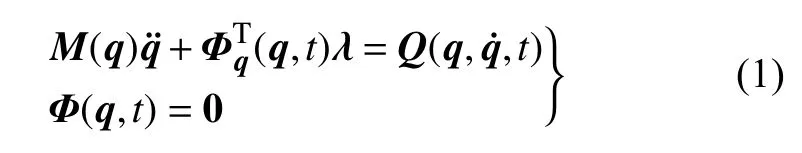
式中,q為系統廣義坐標矢量,M為系統質量矩陣,Q為包含重力,彈性力等的廣義外力矢量.Φ 為約束方程,Φq為約束方程的雅可比矩陣,由 Φ對q求偏導獲得,λ 為拉格朗日乘子.

實際工程應用中由于生產工藝,外界環境等影響,物理系統的參數往往呈現不確定性.當采用區間模型描述參數的不確定性時,不確定參數的變化由區間的上下邊界限制,此時只需獲得參數的上下邊界信息即可.考慮物理系統中的不確定參數由一組區間矢量定義,如下式

此時區間微分代數方程的解可由一組集合描述

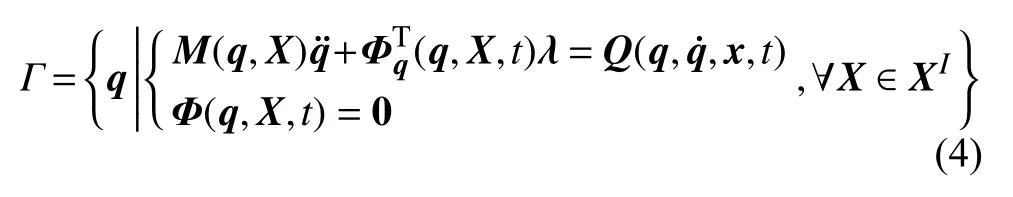
由于式(3)的精確解集合往往呈現非凸流形,往往采用精確解集的最小超立方近對其近似[25],此時,區間方程的響應可由相應的區間邊界表達

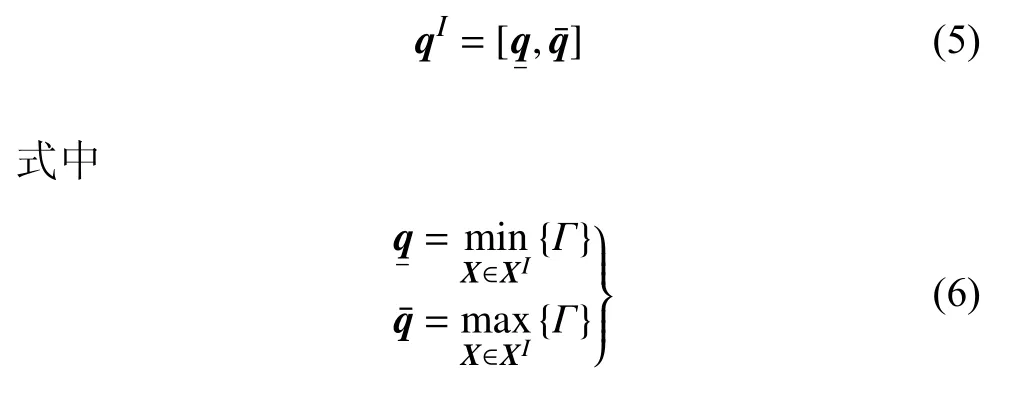
1.2 切比雪夫區間方法

Wu 等[10]首先基于切比雪夫多項式提出切比雪夫區間方法(CIM),作為一種非嵌入式方法,該方法已廣泛應用于多體系統的區間不確定量化[26-28].根據Weierstrass 理論,定義在區間[a,b]上的實值連續函數可由多項式近似,而切比雪夫多項式具有最佳展開多項式之稱.對于一維問題,定義在[a,b]上的p階切比雪夫級數為

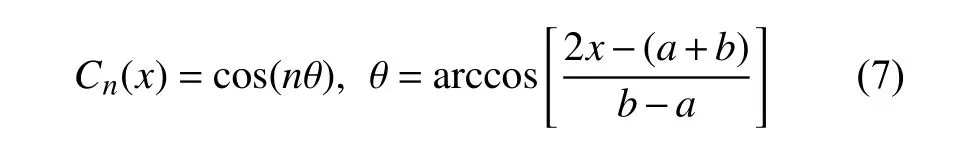
式中,變量x∈[a,b] 且 θ ∈[0,π] .

則單變量連續函數f(x)∈[a,b] 可近似為

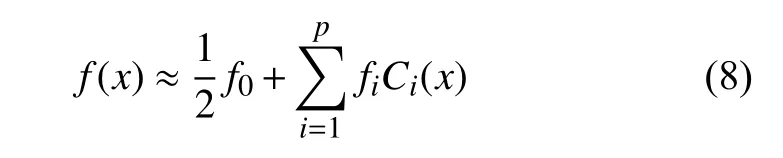
式中,fi為多項式的系數.

對多維問題,切比雪夫多項式是每個一維多項式的張量積.k維切比雪夫多項式定義為

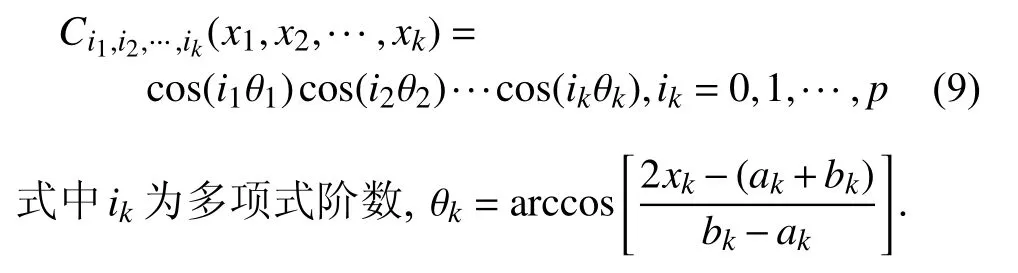
此時,多維函數f(x)=f(x1,x2,...,xk) 可以由n階切比雪夫多項式近似為

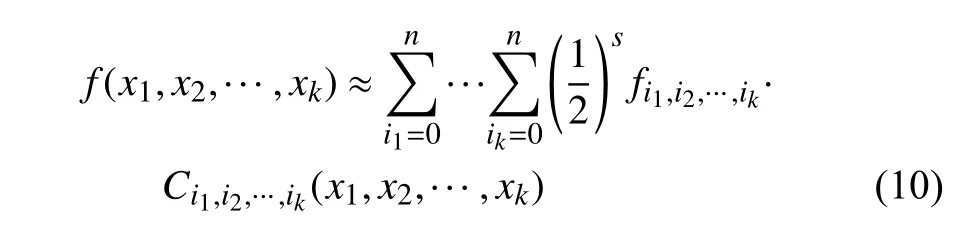
式中,s為下標i1,i2,···,ik中零的數目.

此時,切比雪夫多項式的系數可由Mehler 積分得到

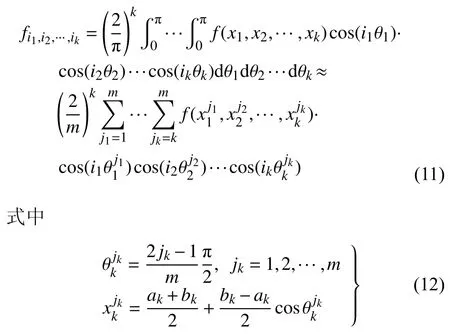
式中,m為多項式插值點數,一般為保證近似精度,取m=p+1.

至此,可通過切比雪夫多項式構建響應函數的代理模型,對構建的代理模型運用掃描法可得到系統輸出響應的上下邊界.

2 基于信號分解的切比雪夫區間方法

2.1 希爾伯特-黃分解

希爾伯特-黃變換[29]包含兩個步驟,經驗模態分解(empirical mode decomposition,EMD) 和Hilbert 變換(HT).EMD 的基本理念為將一個信號分解為多個本征模函數(intrinsic mode functions,IMFs)之和,進一步采用HT 變換可得到每個IMF 對應的瞬時幅值(instantaneous amplitude,IA)和瞬時相位(instantaneous phase,IP).

對于初始的信號x(t),EMD 的分解步驟如下:

(1) 取初始殘差信號ri(t) 等于初始信號x(t),并使hi j(t) 與ri(t) 相等.其中i為IMF 的個數,j為對應第i個IMF 的篩選次數.初始時,i和j都為0.

(2) 識別并提取hi j(t) 所有的局部極大值和極小值.

(3) 在局部極小值點和極大值點上基于三次樣條插值得到極值的上包絡線emax(t) 和下包絡線emin(t),定義上下包絡的均值為

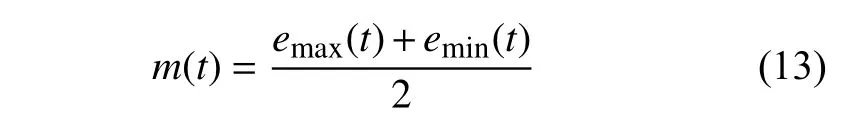
(4) 從hi j(t) 分離出m(t),并將結果賦值給hij(t),有

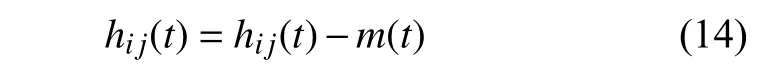
(5) 重復步驟(2)～(4),直至hi j(t) 的均值為零,篩選過程的終止準則為

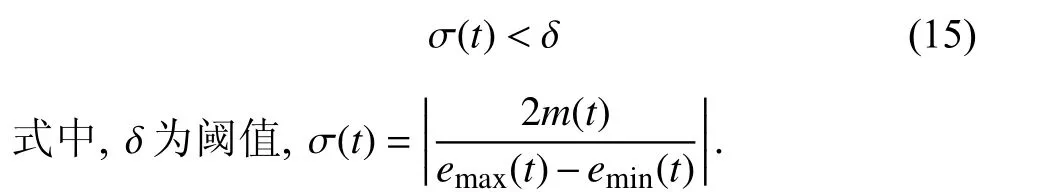
(6) 當篩選準則滿足時,將最終的hi j(t) 構建為一個本征模態函數ci(t),即

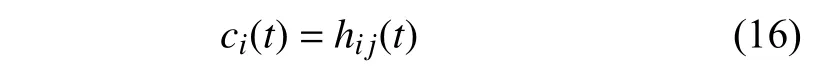
(7) 計算新的殘差信號ri(t)

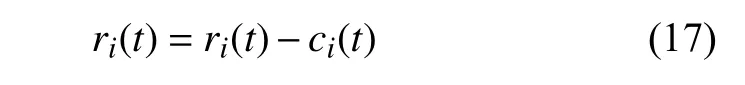
(8) 將殘差ri(t) 賦值給新的hi j(t) .重復上述分解步驟(2)～(7),直至分解停止準則滿足.取迭代步數為n,通過EMD 分解,信號x(t) 可分解為

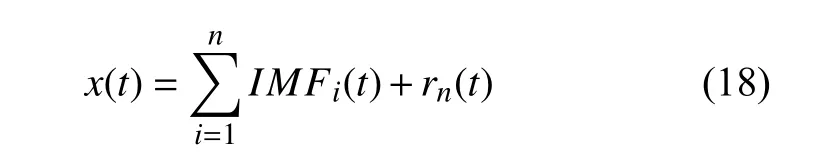
從上述步驟可以看出,EMD 包含內循環和外循環兩個循環,內循環為篩選過程,外循環為分解迭代過程.此外,可將最大的IMFs 個數作為分解停止準則,將最大的移位過程個數作為篩選終止準則.

進一步,對每個IMF采用希爾伯特變換(HT)可獲得瞬時幅值IA 和瞬時相位IP[30],對于信號y(t),其HT 變換定義為

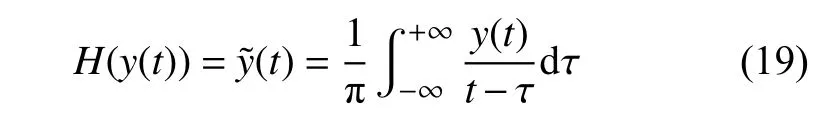
式中,H(·) 為HT 函數.此時,信號z(t) 為

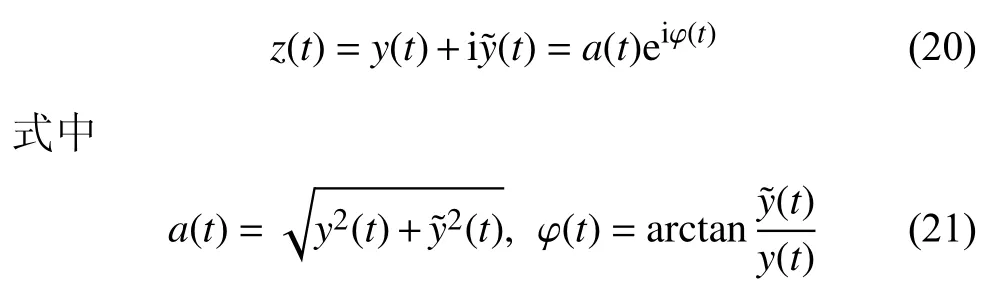
可以看出,z(t) 的實數部分為原始信號y(t),虛數部分為HT 變換得到的虛信號.

此時,信號x(t) 可以通過HHT 分解為

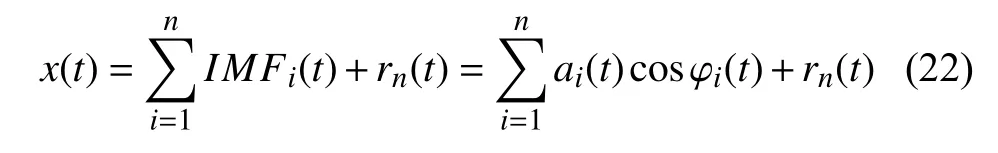
2.2 局部均值分解

局域均值分解(local mean decomposition,LMD)將單一信號分解為幾個積函數(product functions,PFs)之和,每個積函數為一個包絡信號和一個純調頻信號的乘積[31-32].對于初始信號x(t),LMD 的主要步驟如下:

(1) 取x(t) 為初始殘差信號ui(t),并使sij(t)=ui(t) .其中i為PF 的數目,j為第i個PF對應的篩選次數.初始篩選時,i和j都為0.

(2) 確定sij(t) 的所有極值ni jk,其中k表示所有極值中的第k個極值.對兩個連續的極值ni jk和ni j(k+1),第k段的局域均值mi j(t) 為

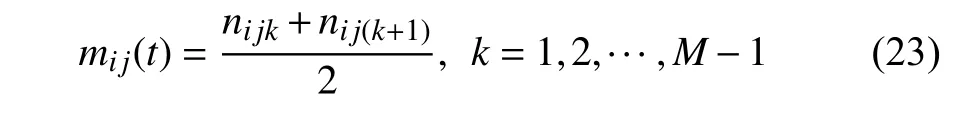
式中,M為極值的總數.兩個連續極值ni jk和ni j(k+1)之間第k段的局部幅值ai j(t) 為

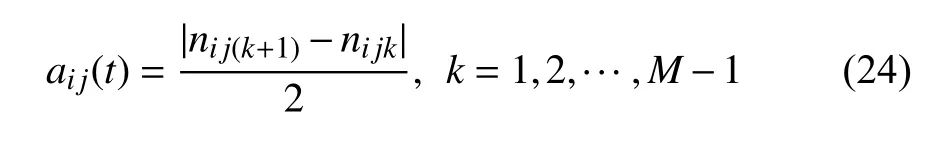
(3) 采用滑動平均法(moving average method)[31]對mi j(t) 和ai j(t) 進行滑動平均,直到任何相鄰點不再相等,其中滑動平均法的步長為mi j(t)或ai j(t) 的最大步長的三分之一.

(4) 從sij(t) 中 分離出mi j(t) 并 將結果賦值給hi j(t),即

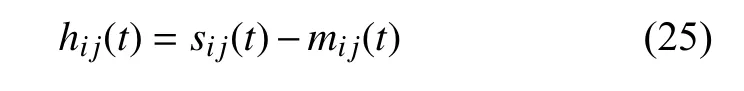
再將ai j(t) 除以hi j(t) 并將結果賦值給sij(t)

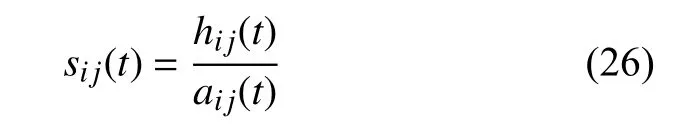
(5) 重復上述篩選過程(2)～(4),直至sij(t) 為純調頻信號,相應的篩選終止準則為

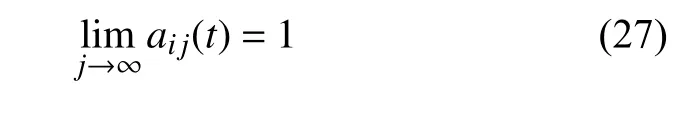
(6) 篩選過程終止后,第i次篩選結束時,假設此時j取值為li,則第i個PF的IA 為

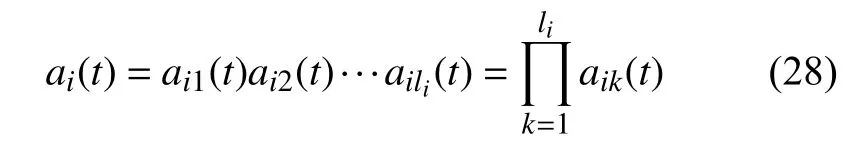
第i個PF的IP 為

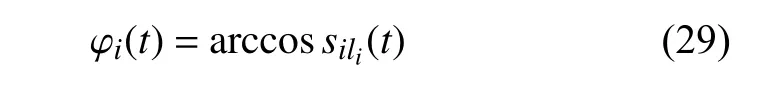
則第i個PF可寫為

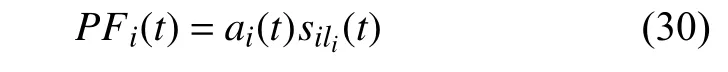
(7) 計算殘差信號

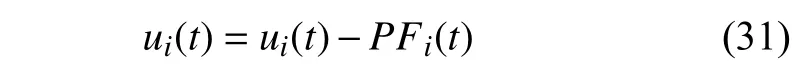
(8) 將新的殘差信號ui(t) 作為新的sij(t),重復上述篩選過程(2)～(7),直至滿足分解終止準則,此時,原始信號可分解為

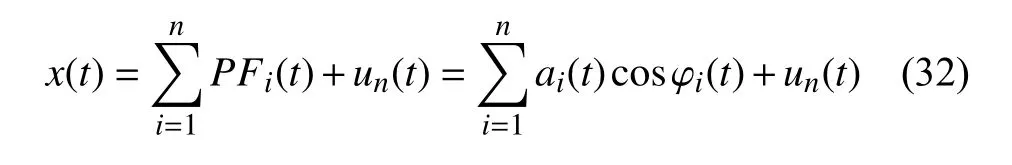
注意到HHT 和LMD 都基于原始信號的極值進行分量篩選,因此當原始信號的端點不是極值點時,會使得分解得到的結果產生偏差,即末端效應.本文采用鏡像延拓法[33]以減弱HHT 和LMD 篩選過程中的末端效應.

2.3 CIM-HHT 方法和CIM-LMD 方法

信號分解的方法可以將一個多分量信號分解為多個單分量分信號,HHT 和LMD 分解只作用于信號本身,因此可以應用于區間不確定分析.本文將HHT 和LMD 分解策略與CIM 結合,提出CIMHHT 和CIM-LMD 兩種方法,以解決CIM 方法在求解含區間參數動力學響應邊界中面臨的邊界退化問題.CIM-HHT 和CIM-LMD 的主要步驟如下:

(1) 根據CIM 方法,生成區間不確定參數X的樣本點,代入確定性DAE 求解器得到每個樣本點對應的響應;

(2) 對每個樣本響應在每個時間步長上進行HHT 和LMD 分解,得到m個單組分響應cj和一個殘差r(t) .每個單組分響應可以由瞬時相位和瞬時幅值的和近似

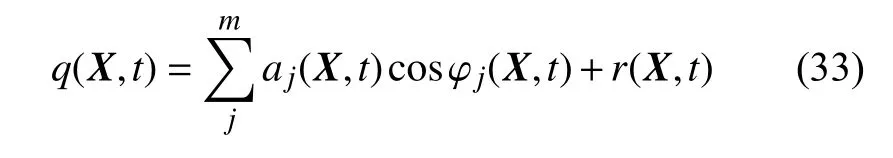
(3) 每個樣本響應分解得到的每個瞬時幅值(IA),瞬時相位(IP)和殘差,基于切比雪夫多項式構造代理模型

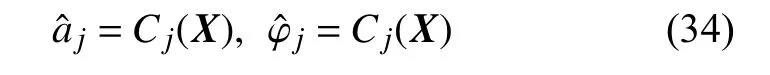
式中,C(·) 表示構建切比雪夫代理模型的過程.

CIM-HHT 方法和CIM-LMD 方法的計算流程如圖1 所示.

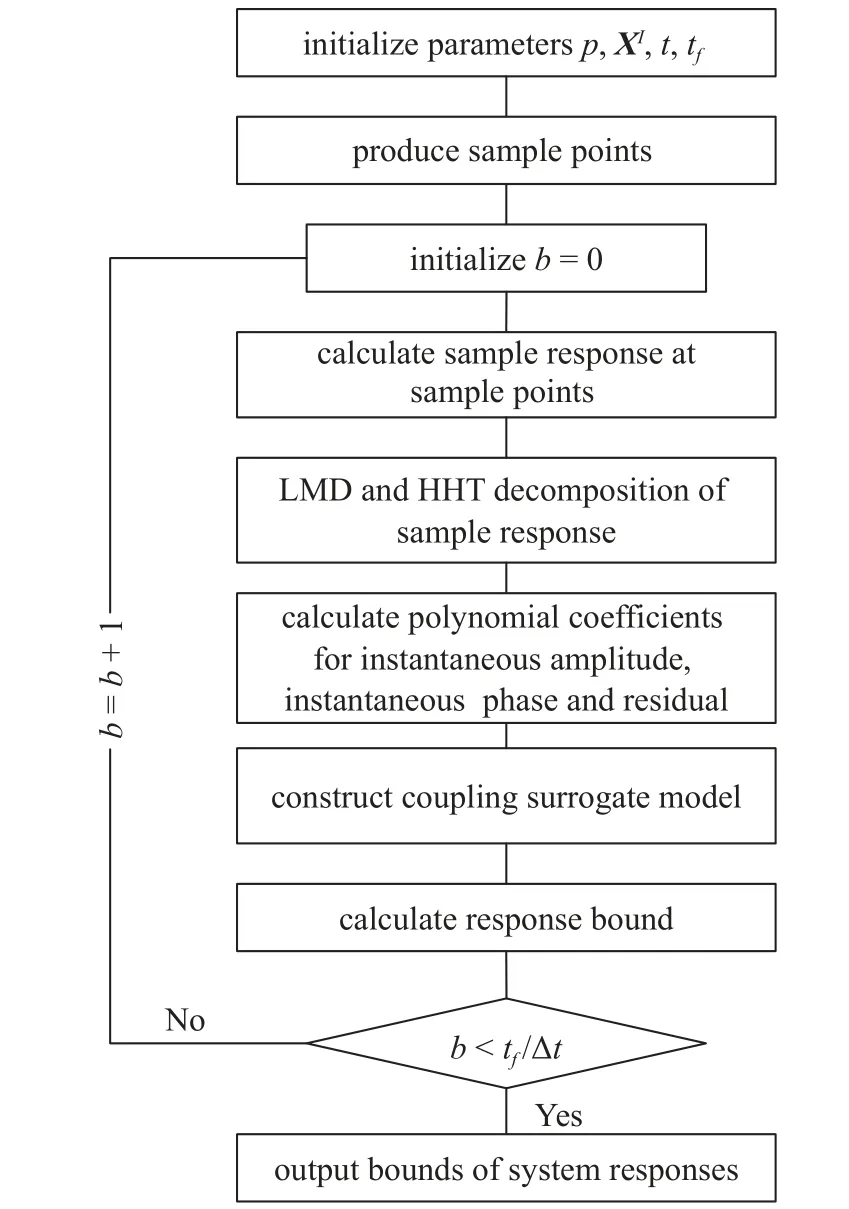
圖1 CIM-HHT 和CIM-LMD 計算流程Fig.1 Flowchart for CIM-HHT and CIM-LMD

3 算例分析

3.1 算例1:單擺

本節以剛性擺為例,對CIM-HHT 和CIMLMD 進行長周期區間分析的有效性進行驗證.剛性擺如圖2 所示,單擺在重力作用下由初始角度釋放.單擺長度為1.8 m,初始釋放角度為 π/3 .

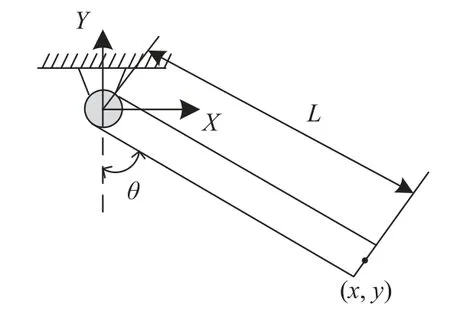
圖2 單擺Fig.2 Simple pendulum

考慮單擺長度的不確定性,對單擺末端點的位移響應進行仿真.其中單擺長度區間不確定度為5%,仿真時間50 s.為驗證本文方法的有效性,采用掃描法和切比雪夫區間方法進行對比,其中掃描點數為100,切比雪夫多項式的階數為4.

采用HHT 和LMD 對不確定參數取中點處的值時,對末端點x方向的位移和速度進行分解,得到的結果如圖3 所示.可以看出HHT 和LMD 將位移響應和速度響應分解為1 個單分量和1 個殘差分量之和,兩種分解方法得到的瞬時相位保持一致,且都呈現單調遞增的特性.相比之下,HHT 得到的瞬時幅值呈現上下振蕩的特點,而LMD 得到的瞬時幅值變化很小,基本保持不變.由于末端效應的影響,HHT 得到的瞬時幅值在兩端波動較為劇烈,可見LMD 末端效應較HHT 更弱.

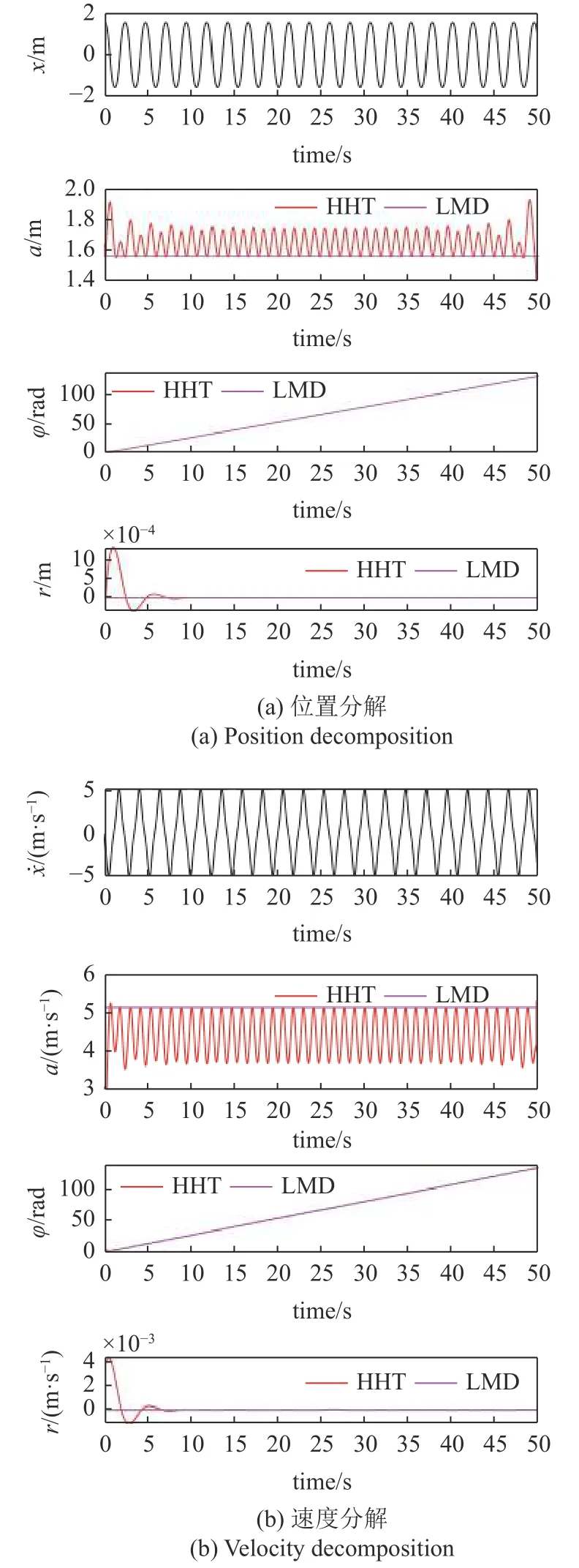
圖3 末端位置和速度的HHT 和LMD 分解Fig.3 HHT and LMD decomposition of position and velocity response of end-tip

為研究不同樣本下系統響應的HHT 分解和LMD 分解特性,圖4 給出了第1、第3 和第5 個切比雪夫多項式零點處的末端位置響應分解.從圖中可以看出,不同樣本響應下,HHT 得到的瞬時幅值振蕩,各個分量之間存在相位差,而LMD 分解得到的瞬時幅值基本保持不變,此時基于LMD 分解構建的代理模型也更為準確.

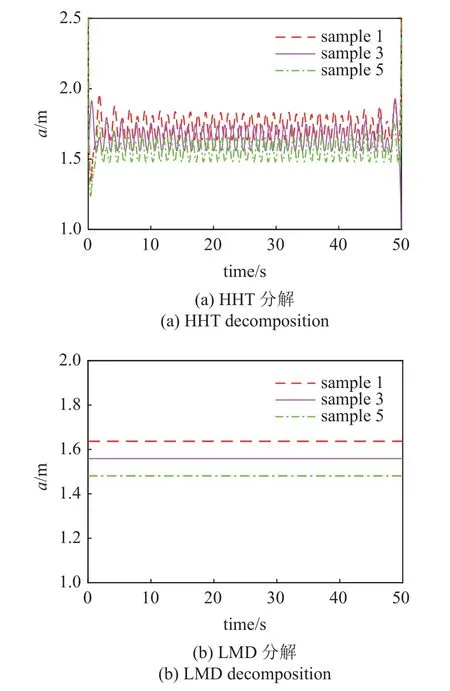
圖4 不同樣本的末端位置響應分解Fig.4 Decomposition of position response of end tip under different samples

圖5 給出了末端位置x方向的響應上下邊界.顯然,隨著時間的增大,CIM 得到的邊界精度逐漸降低,這是由于不同樣本的相位差產生的IPDA 效應造成的.CIM-HHT 與掃描法得到的邊界則較為接近,CIM-LMD 得到的邊界與掃描法得到邊界則基本一致.同時,相比LMD,HHT 的末端效應更為明顯,這也反映在CIM-HHT 獲得的區間邊界上.通過引入信號分解技術,可避免CIM 方法在長周期區間動力學響應分析中產生的邊界惡化問題.

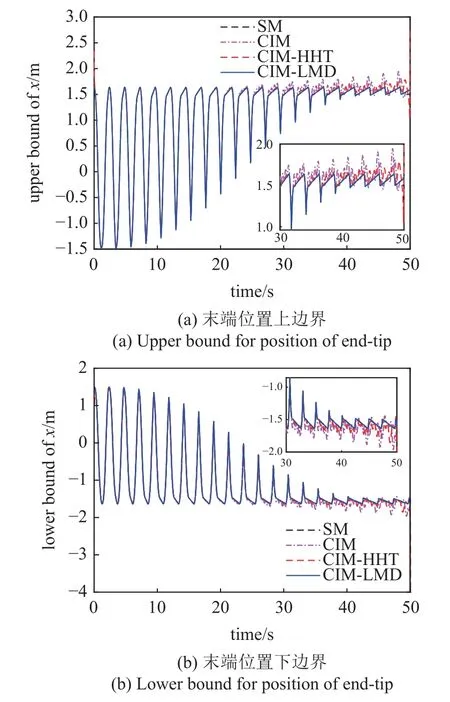
圖5 末端位置響應邊界Fig.5 Bounds for position responses of end-tip

圖6 給出了末端點x方向的速度響應的上下邊界.與圖5 中的結論類似,相比CIM,CIM-HHT 和CIM-LMD 能夠在長周期區間分析中得到更準確的結果.此外,在速度響應中,相比位置響應,隨著時間的增大,CIM 方法產生的區間惡化更為劇烈,這與響應與不確定參數的關系有關.當響應的非線性越強時,隨著時間的增大,樣本響應產生的IPDA 效應越強,CIM 得到的邊界精度越低.從圖6 中可以看出,CIM-LMD 對IPDA 效應抑制效果更好,得到的結果與掃描法的結果基本一致.

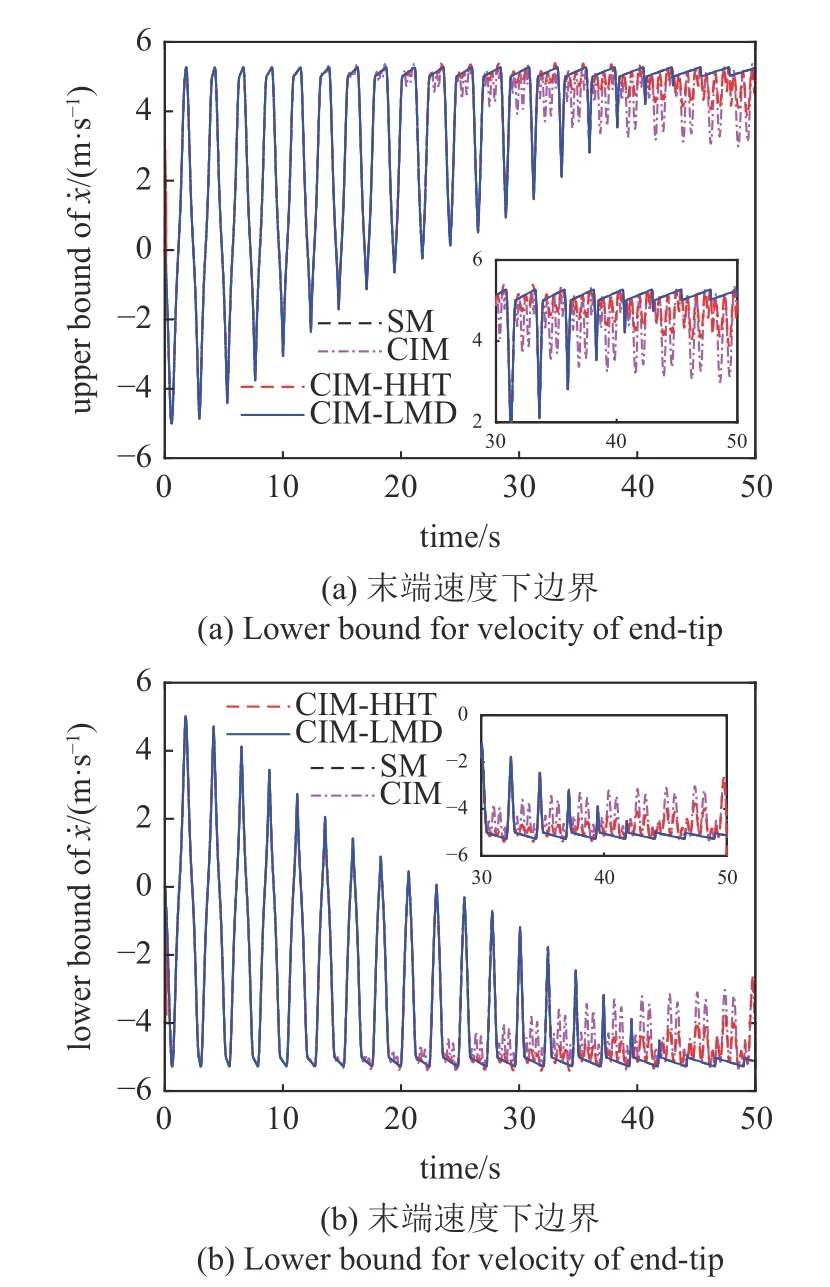
圖6 末端速度響應邊界Fig.6 Bounds for velocity responses of end-tip

進一步,將本文方法與文獻[24]中的方法進行比較,圖7 為由RS-HHT 和RS-LMD 得到的末端位置的響應邊界.從圖7(a)中可以看出,與RS-HHT 得到的響應邊界相比,CIM-HHT 得到的響應邊界更為保守.由于HHT 分解得到的瞬時幅值隨時間振蕩,且不同樣本響應的瞬時幅值之間存在相位差,使得響應的瞬時幅值與不確定參數之間的關系隨著時間增長越來越復雜,采用切比雪夫多項式對瞬時幅值的逼近精度較高,因此CIM-HHT 得到的邊界更為保守.而在圖7(b)中,CIM-LMD 和RS-LMD 得到的響應邊界基本一致.由于LMD 分解得到的位置響應的瞬時幅值基本保持不變,此時瞬時幅值相對于不確定參數的關系呈現弱非線性,RS 和CIM 都能獲得理想的近似精度,兩種方法得到的響應邊界基本一致.

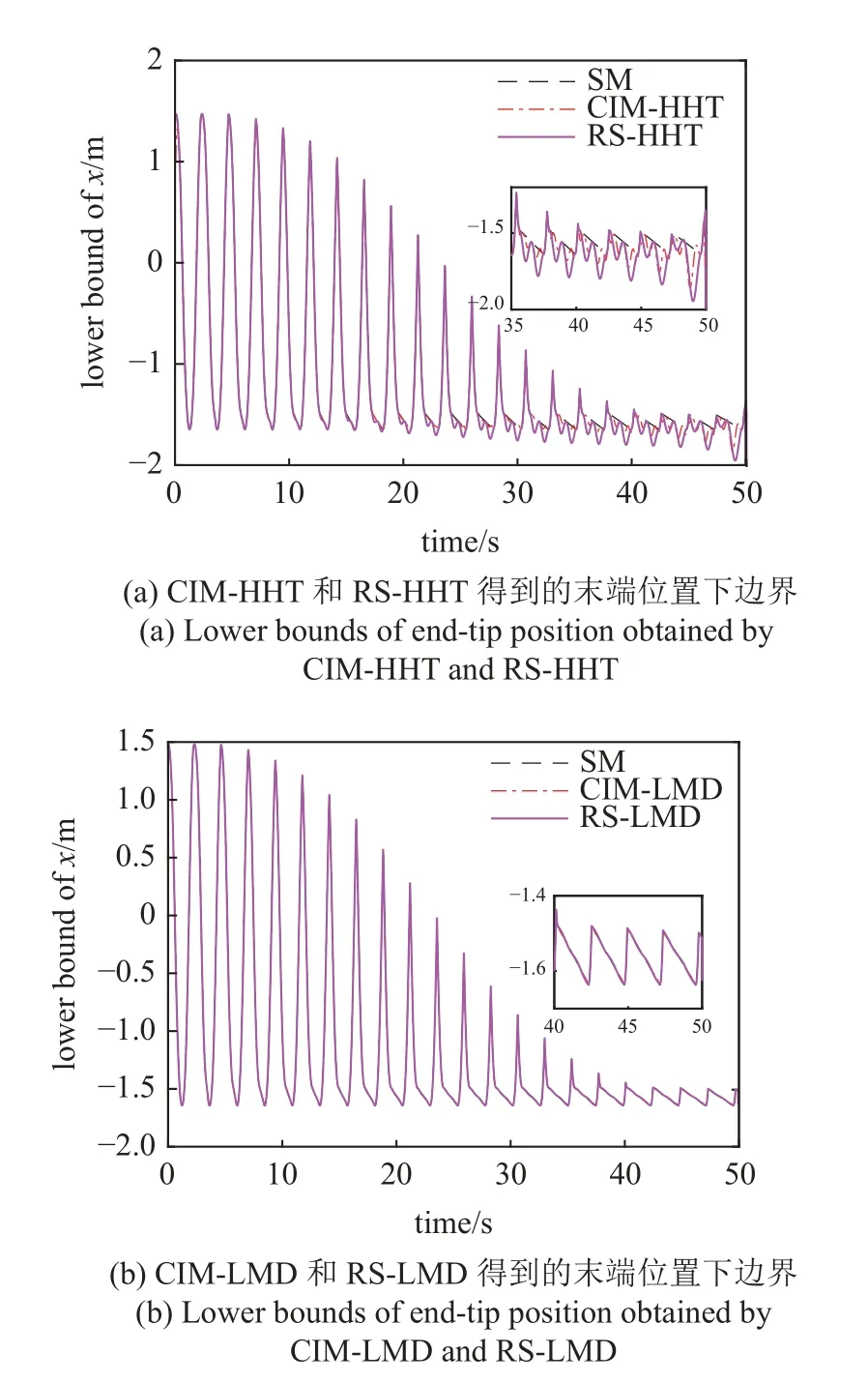
圖7 不同方法得到的位置響應邊界Fig.7 Bounds for position responses of end-tip obtained by different methods

3.2 算例2:曲柄滑塊機構

為進一步驗證CIM-HHT 和CIM-LMD 方法對非線性響應邊界獲取的有效性,以曲柄滑塊機構為例,如圖8 所示研究CIM-HHT 和CIM-LMD 分析曲柄滑塊機構的長周期區間響應.曲柄機構的參數如表1 所示.

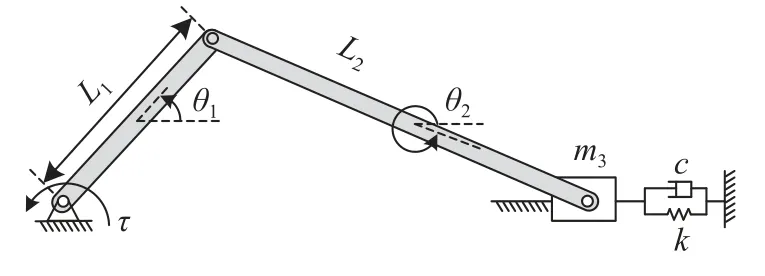
圖8 曲柄滑塊機構示意圖Fig.8 Schematic diagram for crank slider

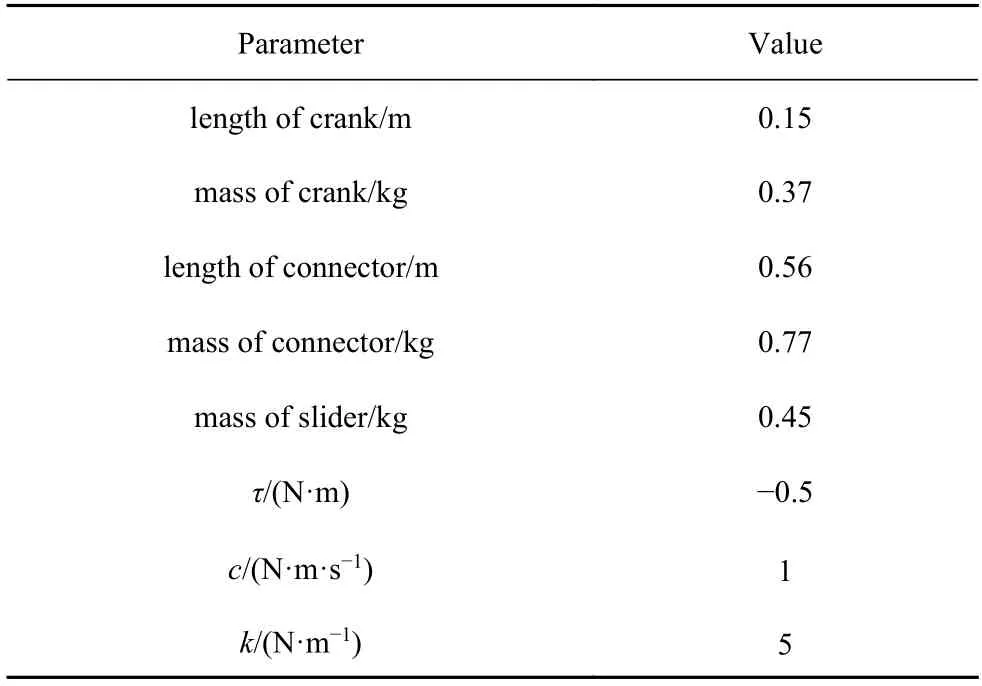
表1 曲柄機構參數Table 1 Parameters for crank slider

考慮曲柄長度的參數不確定性,此時L1為區間數=L1(1±1%) .仿真時間6 s,其中掃描法樣本點數為50,切比雪夫多項式階數為4.

圖9 為在不確定性參數取中點處的值時,對滑塊速度和位移響應的HHT 和LMD 分解結果.由圖可知,HHT 和LMD 將滑塊位置和速度響應分解為1 個單分量和1 個殘差分量.圖9(a) 中可以看出,HHT 分解得到的瞬時幅值上下波動,而LMD 分解得的瞬時幅值基本保持不變.在圖9(b)中,LMD 分解得到的瞬時幅值單調變化,而HHT 得到是瞬時幅值上下振蕩,且越來越劇烈.

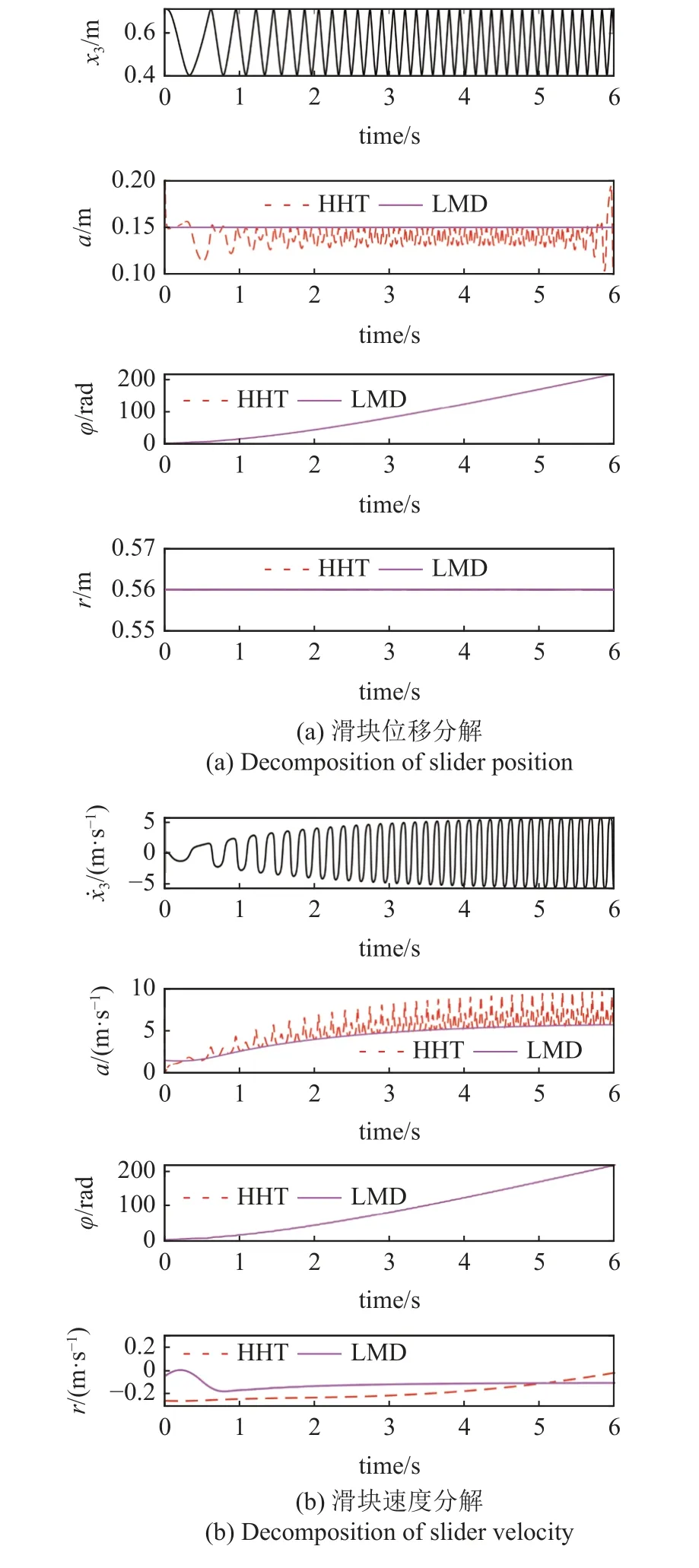
圖9 滑塊位移和速度響應的HHT 和LMD 分解Fig.9 HHT and LMD decomposition for position and velocity response of slider

圖10 給出了考慮區間不確定參數的滑塊位移響應的上下邊界.從t=2 s 后,隨著時間的增大,由于IPDA 效應,CIM 得到上下邊界精度越來越低.CIM-HHT 和CIM-LMD 則能夠保持較好的精度,CIM-LMD 獲得的邊界與參考值基本一致,且具有更弱的末端效應,說明CIM-LMD 能夠更好地應用于長時間區間動力學響應分析.

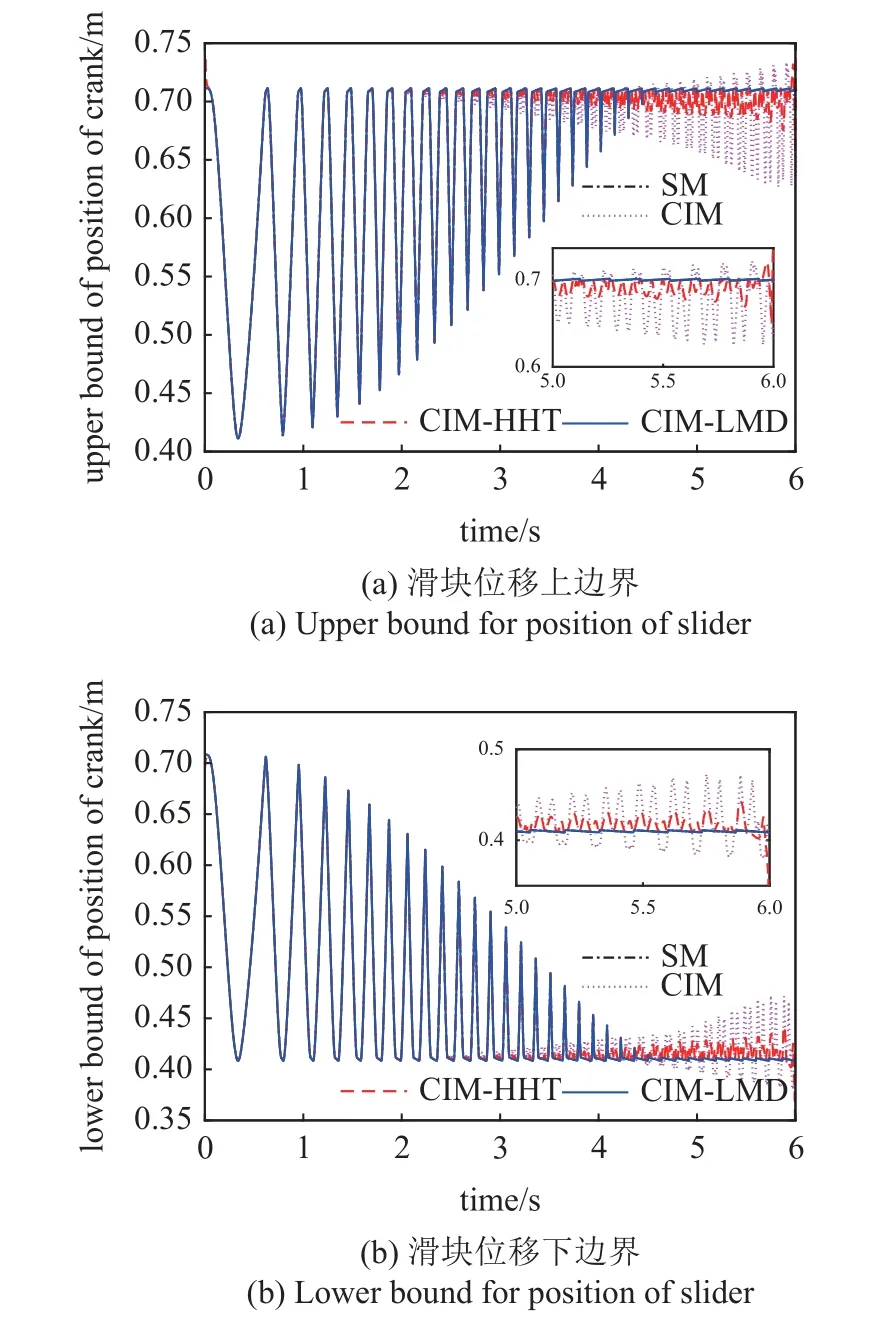
圖10 滑塊位移響應邊界Fig.10 Bounds for position response of slider

滑塊速度響應的上邊界如圖11 所示,可以看出CIM-HHT 得到的上邊界隨時間增大也出現了精度降低,這與HHT 分解得到的瞬時相位相關.如圖9(b)所示,HHT 分解得到的瞬時相位振蕩劇烈,而LMD分解得到的瞬時相位單調變化.相比位移響應,滑塊速度響應具有更強的非線性,此時,CIM-LMD 能夠獲得更準確的數據.

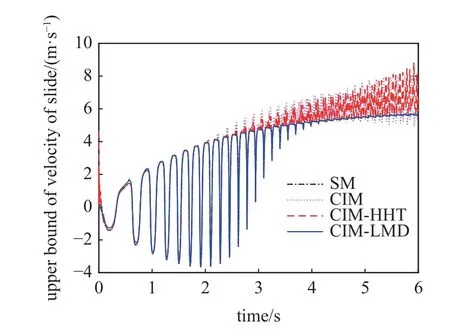
圖11 滑塊速度上邊界Fig.11 Bounds for position responses of slider

圖12 為曲柄角度上下邊界隨時間變化趨勢.顯然,CIM,CIM-HHT 和CIM-LMD 得到的結果與掃描法得到的結果吻合較好,這是因為曲柄轉角響應為單調變化,樣本響應間不存在IPDA 效應,因此在長周期區間分析中CIM 能夠獲得準確的結果.

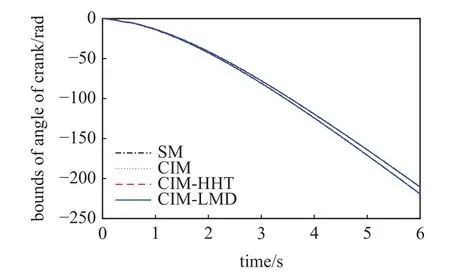
圖12 曲柄角度邊界Fig.12 Bounds for angle of crank

曲柄角速度響應邊界如圖13 所示,在CIMHHT 和CIM-LMD 中,不確定參數的每個樣本響應由HHT 和LMD 分解為2 個單分量響應和1 個殘差分量.從圖中可知,隨著時間增大,在t=2.5 s 之后,CIM 得到邊界精度越來越低,而CIM-HHT 和CIMLMD 能夠保持較好的計算精度.在仿真初期和末期,由于末端效應,CIM-HHT 和CIM-LMD 與掃描法的結果存在微小的偏差.注意到CIM-HHT 在t在0～1 s 之間的結果產生的偏差更大,這是由于HHT 分解中的模態混疊導致的[34].

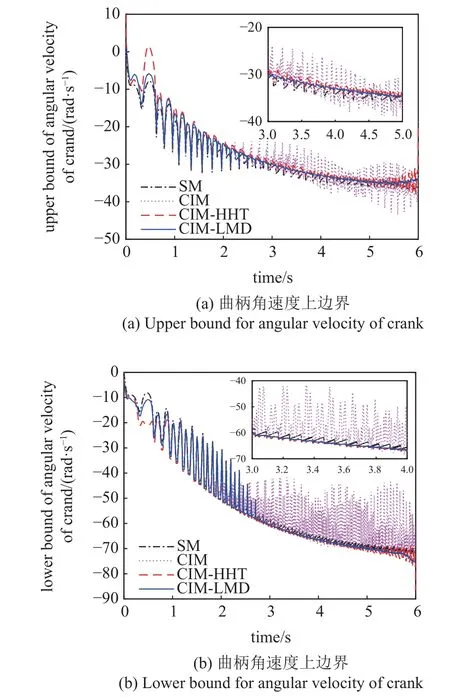
圖13 曲柄角速度邊界Fig.13 Bounds for angular velocity of crank

進一步,圖14 給出了RS-HHT 和RS-LMD 方法得到的滑塊速度響應下邊界.由圖可知,RSLMD 和CIM-LMD 得到的響應邊界曲線基本一致,而CIM-HHT 相比RS-HHT,得到的響應邊界隨著時間增長邊界惡化效應減弱,與算例1 中圖7 得到的結論一致.

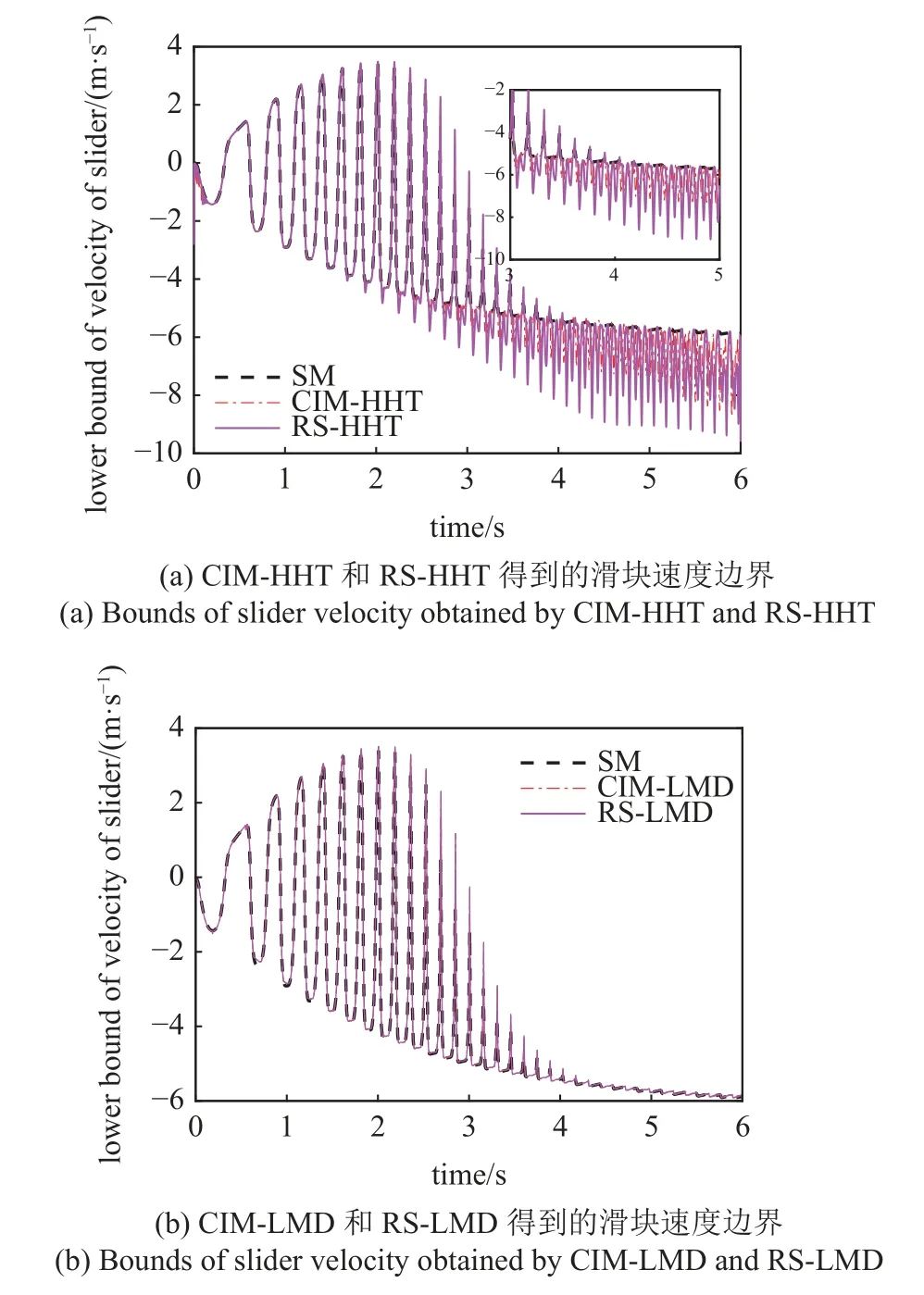
圖14 不同方法得到的滑塊速度響應邊界Fig.14 Bounds for response of slider velocity using different methods

為了進一步說明本文方法的有效性,考慮曲柄長度和質量在區間內變化,參數不確定度為5%,此時有

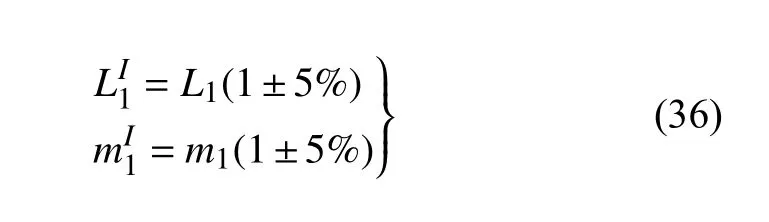
采用RS-LMD 和CIM-LMD 計算系統的響應邊界,在RS-LMD 和CIM-LMD 中多項式的階數均為2,對代理模型的掃描樣本數為50,仿真計算結果如圖15 所示.由圖可知,CIM-LMD 得到的響應邊界與參考邊界基本一致,相比之下,RS-LMD 得到的響應邊界存在一定的偏差.其原因在于,在RS-LMD 中瞬時幅值、瞬時相位和殘差的耦合代理模型基于泰勒多項式構建,而在CIM-LMD 中基于切比雪夫多項式構建耦合代理模型.由于泰勒多項式為局部近似,而切比雪夫多項式在整個區間上一致近似[35],因此當參數不確定度增大時,CIM-LMD 對瞬時幅值、瞬時相位和殘差的逼近更準確,從而能夠獲得更準確的耦合代理模型,得到的響應邊界更為保守.

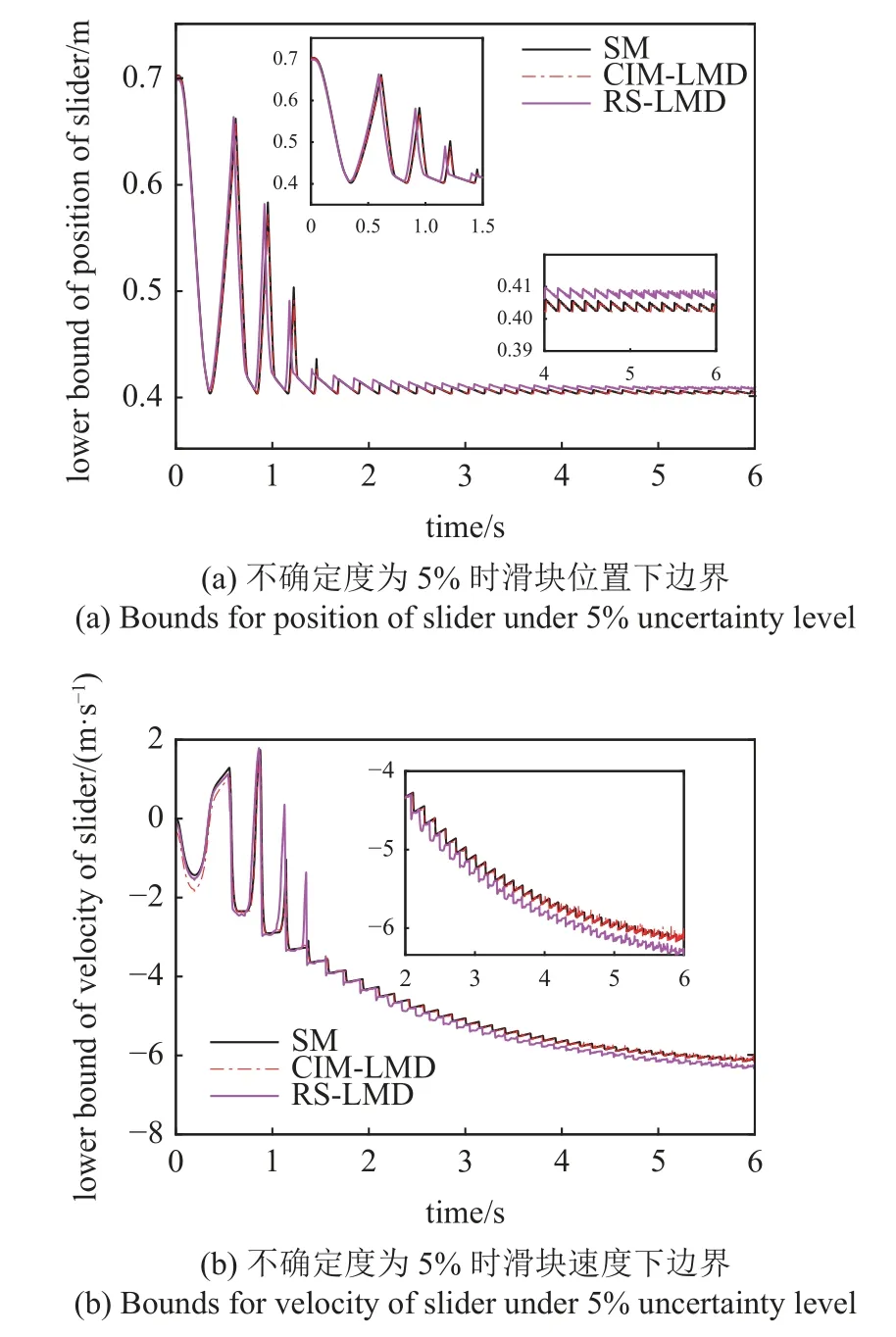
圖15 不確定度為5%時CIM-LMD 和RS-LMD 得到的響應邊界Fig.15 Bounds of responses using CIM-LMD and RS-LMD under 5% uncertainty level

4 結論

針對傳統的切比雪夫方法在處理多體系統長周期區間動力學響應邊界計算時出現的邊界惡化問題,本文提出了基于信號分解技術的CIM-HHT 和CIM-LMD 方法.HHT 和LMD 能夠將系統響應分解為多個單分量響應之和,對每個單分量的幅值和相位基于切比雪夫多項式構建代理模型,進一步得到系統的響應邊界.通過數值算例研究,得到以下結論.

(1) CIM-HHT 和CIM-LMD 能夠將非線性、非平穩響應分解為多個弱線型、單分量響應之和,適用于含區間不確定性多體系統長周期動力響應分析.

(2)相比CIM,CIM-HHT 和CIM-LMD 能夠在一定程度上改進CIM 方法由于響應相位差累積導致的邊界精度下降問題.

(3)相比CIM-HHT,CIM-LMD 具有更弱的末端效應,更平穩的分解過程,在多體系統區間不確定分析中計算精度更高.