非線性O(shè)DE-PDE耦合系統(tǒng)邊界控制的局部鎮(zhèn)定①

何翠華， 王科， 甯懿楠

成都工業(yè)學(xué)院 大數(shù)據(jù)與人工智能學(xué)院， 成都 611730

耦合的ODE-PDE系統(tǒng)廣泛存在于工程問題中． 近年來， 大量文獻采用 Backstepping 變換方法來解決常微分方程和偏微分方程之間的耦合問題． 為滿足工程需要， 我們利用邊界條件設(shè)計控制律來控制這些耦合的ODE-PDE系統(tǒng)使其穩(wěn)定在平衡狀態(tài)． 邊界控制律是由PDE Backstepping 控制發(fā)展而來[1-4]．

ODE-PDE耦合系統(tǒng)邊界控制大多是線性的[5-15]， 然而非線性現(xiàn)象在應(yīng)用數(shù)學(xué)和物理中廣泛存在． 耦合的線性常微分方程和非線性偏微分方程系統(tǒng)具有豐富的工程應(yīng)用價值， 但由于非線性在數(shù)學(xué)上是極具挑戰(zhàn)性的問題， 故關(guān)于非線性偏微分方程系統(tǒng)鎮(zhèn)定的結(jié)果較少[15-22]． 利用邊界控制來穩(wěn)定非線性O(shè)DE-PDE耦合系統(tǒng)是一個很有意義的研究領(lǐng)域．

本文對非線性O(shè)DE-PDE耦合系統(tǒng)的控制設(shè)計類似于文獻[7]， 主要貢獻是基于邊界反饋控制的方法處理一類包含反應(yīng)項是不確定的非線性偏微分方程與線性微分方程的耦合系統(tǒng)的局部指數(shù)穩(wěn)定的問題．

因此， 本文考慮以下非線性耦合系統(tǒng)的邊界控制

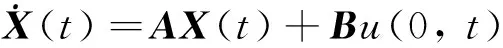
(1)

ut(x，t)=uxx(x，t)+f(u(x，t))，x∈(0， 1)

(2)

ux(0，t)=α(u(0，t)-CTX(t))

(3)

u(1，t)=U(t)

(4)

其中： 向量X(t)∈Rn是裝置的一個信號； (A，B)是可控制矩陣對 (A∈Rn×n，B∈Rn) ； 標(biāo)量u(x，t)∈R是裝置的熱量； 在x=0處， 滿足Neumann邊界條件，α是傅里葉常數(shù)， 它取決于裝置的材料和導(dǎo)熱性，CTX(t)是溫度裝置(CT∈Rn)；U(t)是邊界控制輸入．f(u(x，t))是非線性函數(shù)， 對于這個系統(tǒng)， 非線性f(u)引用文獻[15]假定條件．

假定1對于系統(tǒng)(2)中的f(u)， 存在δ>0和β>1， 使得

f(0)=0

‖f(u)‖≤δ‖u‖β

(5)

其中‖·‖將在后面詳細說明．

假定1中的第一項表示0是系統(tǒng)(1)-(4)在零輸入下的平衡態(tài)， 第二項意味著f(u)的增長速度并不比u的冪函數(shù)快．

系統(tǒng)(1)-(4)代表了一類廣泛的耦合非線性O(shè)DE-PDE方程， 本文主要貢獻是基于 Backstepping 變換的邊界控制方法使一類包含不確定反應(yīng)項的非線性偏微分方程與線性微分方程的耦合系統(tǒng)達到局部指數(shù)穩(wěn)定． 對于ODE-PDE耦合系統(tǒng)Backstepping邊界控制律設(shè)計方法是可行的[1，6-7]． 通過引入具有理想穩(wěn)定性的目標(biāo)系統(tǒng)， PDE Backstepping 變換將系統(tǒng)轉(zhuǎn)化為由核函數(shù)和向量值函數(shù)耦合的方程． 然后根據(jù)目標(biāo)系統(tǒng)的邊界條件得到控制律． 研究PDE Backstepping 變換解決耦合ODE-PDE的控制系統(tǒng)是很有價值的．

本文令

(6)

(7)

1 控制律

1.1 Backstepping變換

引入以下Backstepping變換

X(t)=X(t)

(8)

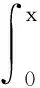
(9)

其中k(x，y)與φ(x)是待定的．

將目標(biāo)系統(tǒng)取為

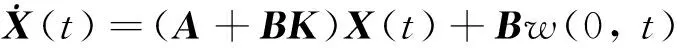
(10)

wt(x，t)=wxx(x，t)+H(w(x，t))，x∈(0， 1)

(11)

wx(0，t)=0

(12)

w(1，t)=0

(13)

其中：

選擇向量KT∈Rn使得 (A+BK)是Herwitz矩陣．

利用(3)，(9)式對w(x，t)關(guān)于x和t求導(dǎo)

(14)

再令

k′(x，x)=0

ky(x， 0)-αk(x， 0)+φ(x)B=0

φ″(x)-αk(x， 0)CT-φ(x)A=0

kxx(x，y)-kyy(x，y)=0

(15)

接著控制律被設(shè)計為

(16)

通過邊界條件(13)獲得．

1.2 核方程的解

為了方便， 引用文獻[14]直接給出(15)式的解． 令

其中I是單位矩陣．

Γ(0)=(K， -αCT，KA+α2CT)

核函數(shù)k(x，y)和φ(x)分別為

φ(x)=Γ(0)eDxJ

1.3 逆變換

同樣我們給出逆變換

X(t)=X(t)

(17)

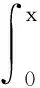
(18)

令

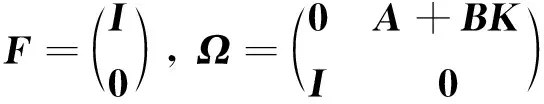
其中I是單位矩陣．

Θ(0)=(K，α(K-CT))

核函數(shù)Ψ(x)和n(x，y)分別為

Ψ(x)=Θ(0)eΩxF

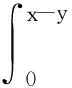
2 穩(wěn)定性

為得到穩(wěn)定性定理， 首先給出幾個引理．

引理1函數(shù)w(x，t)由(6)式定義， (PB)T和X(t)由(7)式定義， 有以下不等式成立

(19)

證現(xiàn)在利用Schwartz’s不等式和Young’s不等式來估計， 可得

接著根據(jù)w(1，t)=0與Agmon’s不等式， 有

然后利用Poincare不等式， 可得

因此， 不等式(19)成立．

引理2根據(jù)變換(9)與逆變換(18)， 可得

‖w(x，t)‖2≤(1+s)‖u(t)‖2+‖φ‖2‖X(t)‖

‖u(x，t)‖2≤(1+t)‖w(t)‖2+‖Ψ‖2‖X(t)‖

(20)

其中：

(21)

(22)

證由變換(9)， 可以獲得

由Holder’s不等式， 可以得到

其中：

(23)

接著根據(jù)Schwartz’s不等式， 有

其中：

因此

‖w(x，t)‖2≤(1+s)‖u(t)‖2+‖φ‖2‖X(t)‖

同理可估計

‖u(x，t)‖2≤(1+t)‖w(t)‖2+‖Ψ‖2‖X(t)‖

其中t和‖Ψ‖2由(22)式定義， 則(20)式成立．

引理3H(w(x，t))由(11)式定義， 可得

(24)

其中：

(25)

證

我們令

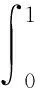
其中：

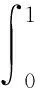
利用Holder不等式 與Young’s不等式， 可得

其中：

由此可得

同理可估計

其中s來自(23)式．

然后

其中ξ是如(25)式所示的常數(shù)．

接下來證明目標(biāo)系統(tǒng)(10)-(13)是局部穩(wěn)定的．

定理1存在一個正常數(shù)γ且任意的初始條件滿足‖X(0)，w(0)‖2≤γ， 有下列不等式成立

(26)

其中

(27)

則目標(biāo)系統(tǒng)(10)-(13)在‖·‖2意義下是局部指數(shù)穩(wěn)定的．

證

考慮以下Lyapunov函數(shù)

(28)

其中矩陣P=PT>0滿足

P(A+BK)+(A+BK)TP=-I

(29)

且參數(shù)a>0是待定的．

矩陣P是(29)式的解， 因此

(30)

其中λmin(P)與λmax(P)是矩陣P的最小和最大的特征值．

對(28)式關(guān)于t求導(dǎo)， 則

代入(19)，(20)和(24)式可以得到

令a=8‖PB‖2+3， 可得

其中ξ由(25)式定義．

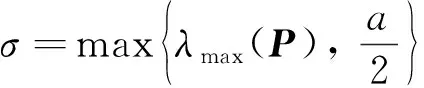
(31)

選取‖X(0)，w(0)‖2≤γ， 則V(0)≤σγ2， 因此不等式(31)成立． 利用(30)和(31)式， 可以推出

其中μ由(27)式定義， 因此不等式(26)成立． 證畢．

3 仿真設(shè)計

系統(tǒng)(1)-(4)的模擬仿真

其中：

f(u(x，t))=12u2(x，t)

同時

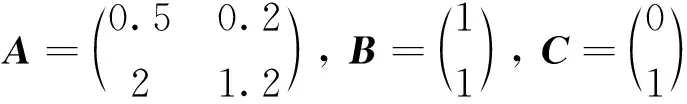
我們令

K=(-0.7， -9.2)

可以驗證矩陣A+BK是Hurwitz矩陣． 因此， 系統(tǒng)滿足(5)式， 容易得到

其中：

Γ(0)=(-0.7， -9.2， 0， -5， -18.75， 13.82)

則控制律為

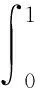
(32)

仿真結(jié)果見圖1-4． 圖1開環(huán)系統(tǒng)是不穩(wěn)定的． 圖2和圖3顯示在控制(32)輸入下， 閉環(huán)系統(tǒng)的信號在時間趨近于無窮時趨近于零． 圖4顯示控制(32)是有界的．

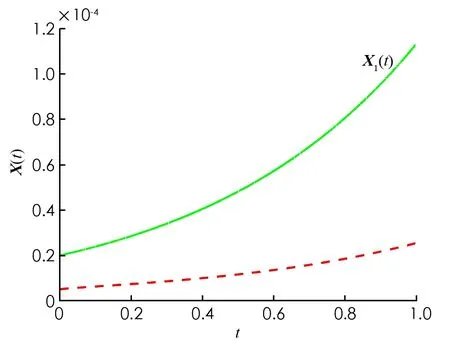
圖1 開環(huán)系統(tǒng)下的X(t)

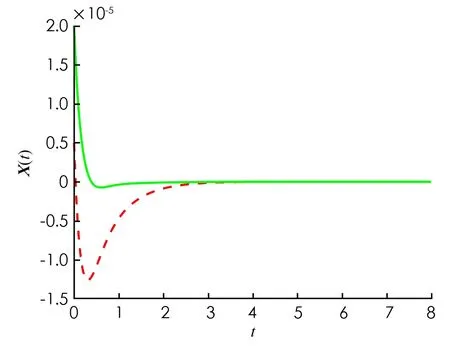
圖2 閉環(huán)系統(tǒng)下的X(t)

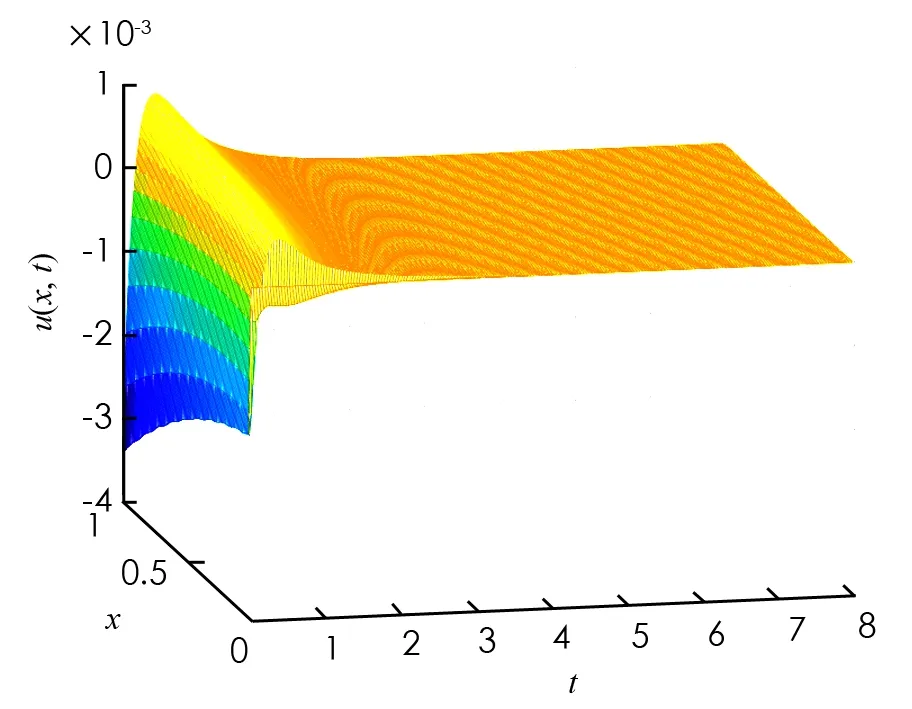
圖3 閉環(huán)系統(tǒng)下的u(x， t)

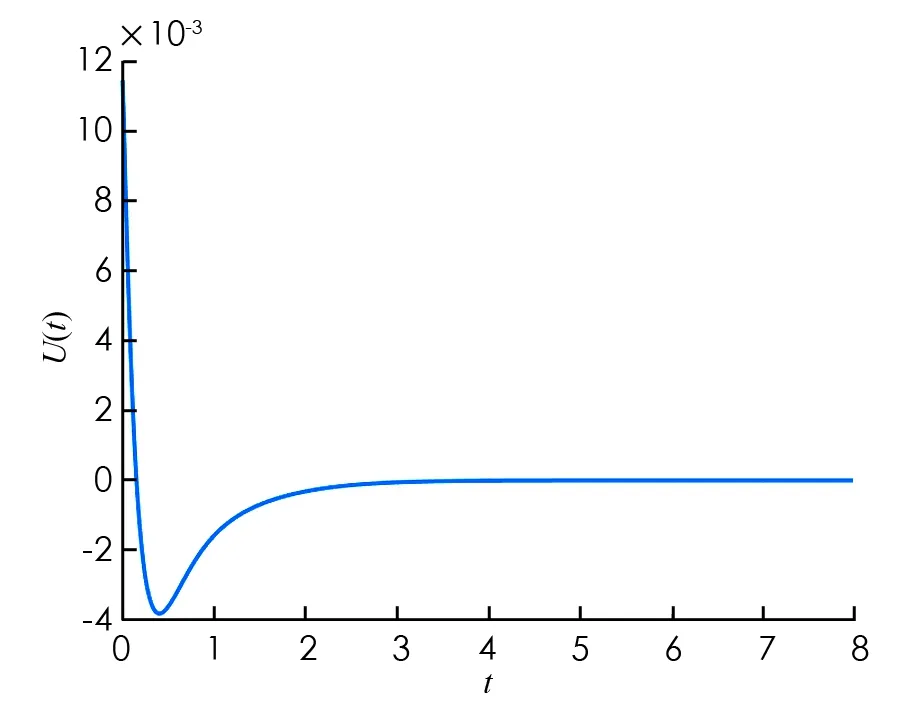
圖4 U(t)的輸入