無人機聯合D2D應急通信網絡的性能分析

衛海超， 張家紅， 劉銘岳， 許愛德

(大連海事大學信息科學技術學院， 大連 116026)

當地震、地質及洪澇等自然災害發生后，因災區地勢復雜、氣象惡劣、道路損毀以及各類次生災害頻發等原因，大型裝備無法快速抵達現場、環境難以勘測。除了專業的救援裝備[1]外，快速有效的應急通信手段對于保障救援工作的順利進行具有非常重要的作用和意義。傳統的應急通信手段中，應急衛星通信系統普及率低，傳輸鏈路過長，時延大，很難保證實時通信，且常用商用終端難以支持長距離的衛星通信；應急通信車受交通和道路的影響，短時間內無法到達[2]。D2D(device-to-device)通信與無人機技術的出現，為應急通信網絡的部署提供了一種更加可行有效的應急通信保障方案。

D2D通信作為5G的關鍵技術之一，支持終端直連，可以即時啟用。但其覆蓋范圍小，通信距離有限，無法獨自承擔應急通信需求。而無人機憑借其機動性與靈活性，可不受地形影響，快速進入災區充當臨時基站和中繼[3]，為地面用戶提供服務。因此，在應急通信應用中，將無人機與D2D通信聯合部署，可有效增加應急通信網絡的覆蓋范圍，提高系統的吞吐量。

然而將無人機與D2D通信聯合部署也讓系統內無線資源的分配變得更加復雜，其中系統既可以給D2D通信用戶分配單獨的無線資源，也可以讓D2D通信用戶復用通信系統內無人機通信用戶的無線資源。在復用模式下，D2D通信用戶與無人機通信用戶之間會產生相互干擾。若不對干擾進行有效控制，將會嚴重影響系統的通信性能。

為了對抗干擾，國內外學者提出了不同的資源管理算法與方案[4-6]。具體地，Masaracchia等[4]提出了一種最優功率分配算法，其中將用戶的服務質量要求和用戶接入層的可用功率作為優化約束，聯合優化用戶能量效率和下行鏈路吞吐量。 Miao等[5]設計了一種無人機輔助的D2D無線通信系統，聯合優化速率以及覆蓋性能。Huang等[6]以最大化無人機輔助的無線通信系統的D2D對速率為目標，提出了一種聯合優化無人機和D2D用戶的發射功率、無人機的飛行高度和位置以及地面終端分配的帶寬的迭代算法。但這些算法或方案僅考慮了空中存在單個無人機的網絡場景，所得結果很難應用到大規模通信網絡。在實際無線通信網絡中，無人機和用戶空間分布具有一定的隨機性，基于隨機幾何理論建立網絡模型可以更好地分析與預測不同的網絡性能指標，成為近年來大規模網絡性能評估與理論研究的主要數學工具之一[7-9]。在該研究領域中，Guo等[10]分析了多無人機與D2D通信共存的網絡場景，推導了無人機通信用戶以及D2D通信用戶的成功傳輸概率，結果顯示存在最佳的無人機高度使地面網絡容量最大化。Rihan等[11]考慮了D2D設備隨機分布在多個頻段上的場景，并推導了當D2D通信鏈路復用無人機通信上行鏈路時網絡的成功傳輸概率，進一步分析了達到最佳網絡能效的關鍵網絡參數。 Ji等[12]研究了支持緩存的無人機與D2D通信共存的網絡模型，基于該模型，利用隨機幾何理論推導了該模型下無人機以及D2D通信用戶的成功傳輸概率的閉式表達式，結果表明存在最佳的無人機高度使得無人機的成功傳輸概率最大。

然而，現有分析無人機與D2D通信共存網絡性能的文獻中，研究的都是無人機配備全向天線的場景，雖然覆蓋的角度范圍較大，卻也導致網絡中的干擾鏈路增多。為了提高通信系統的性能，現提出一種無人機配備定向天線陣列的網絡模型，在該網絡中，每個無人機為主瓣波束范圍內的用戶提供服務，通過配置多天線的移相器或者數字波束發送矢量實現波束掃描機制實現類似全向天線的廣域覆蓋。該機制已用于5G NR中下行同步信號的周期性播發。考慮了兩種類型的用戶：從無人機處接收數據的下行鏈路用戶以及彼此直接進行通信的D2D用戶。為了提高頻譜利用率，假設D2D通信全頻復用無人機通信下行鏈路的無線資源(如LTE系統中的資源塊)，即D2D通信用戶需要與無人機通信用戶共享頻譜。基于該模型，利用隨機幾何理論，推導無人機通信用戶以及D2D通信用戶的成功傳輸概率以及速率表達式，并具體分析定向天線以及天線陣子數量對系統性能產生的影響。此外，為了給無人機基站的實際部署提供理論指導，進一步分析無人機高度以及密度對網絡性能產生的影響，以利用最少的資源實現最高的通信性能。

1 系統模型

1.1 網絡模型

選取網絡中的用戶作為主要研究對象，以系統內一個下行鏈路用戶所接收信號為例，其系統框圖如圖1所示。其中無人機的分布服從密度為λu的齊次泊松點過程(homogeneous Poisson point process，HPPP)Φu，下行鏈路用戶的分布服從密度為λd的HPPPΦd，且下行鏈路用戶由最近的無人機進行服務，無人機在恒定發射功率Pu下工作，與地面距離固定為l。D2D用戶的分布服從密度為λd的HPPPΦd，假設D2D發送設備的傳輸功率為Pd，所有地面設備傳輸功率相同，d0為每對D2D用戶中發送設備與接收設備之間的固定距離。

Ri表示第i個無人機在地面的投影到典型下行用戶之間的距離；Rc表示受災區域半徑圖1 系統模型Fig.1 System model

1.2 天線模型

假設每個無人機裝配天線陣子數為N的均勻平面方陣(uniform planar square array，UPA)來執行定向波束賦形，通過5G NR中的波束掃描機制[13]為波束覆蓋范圍內的用戶提供服務。每個無人機的波束覆蓋范圍以及天線增益由波束的四個主要特性決定，即方位角平面的半功率波束寬度φ，仰角平面的半功率波束寬度φ，半功率波束寬度內的天線主瓣增益Gt，半功率波束寬度外的旁瓣增益gt。其中，波束參數與陣列大小之間的關系由表1所示[14]。

假設地面用戶使用全向天線收發信號，即D2D通信收發端天線增益都為1，下行通信鏈路中，用戶接收端天線增益為1，無人機發送端的天線增益G的概率分布為

(1)

式(1)中：p為無人機主瓣波束與地面用戶對齊的概率，則

(2)

表1 均勻平面方陣的波束參數[14]Table 1 Antenna parameters of UPA[14]

1.3 信號干擾比分析

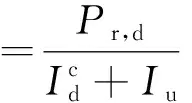
(3)

式(3)中：di為其他D2D發送設備與典型D2D接收設備之間的距離；h0為典型D2D發送設備與接收設備之間的傳輸鏈路信道增益；hi為其他D2D發送設備與典型D2D接收設備之間的傳輸鏈路信道增益；Xj為第j個無人機到典型D2D接收設備之間的距離；Cj為第j個無人機與典型D2D接收設備之間的干擾鏈路信道增益；Gj為第j個無人機與典型D2D接收設備之間的干擾鏈路天線增益。

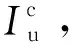
(4)

2 性能分析

本節給出了D2D用戶成功傳輸概率的精確表達式，以及以配備定向天線的無人機為基站，下行鏈路用戶成功傳輸概率的上下界理論表達式。

2.1 D2D用戶的成功傳輸概率

成功傳輸概率定義為典型用戶SIR的互補累積分布函數(complementary cumulative distribution function，CCDF)，表示為

P(θ)=P(SIR >θ)

(5)

式(5)中：θ表示目標SIR閾值。首先對D2D用戶的成功傳輸概率進行分析，可得到精確的D2D用戶成功傳輸概率表達式。

定理1令q=1-p，σd=2/αd，D2D用戶的成功傳輸概率為

(6)

(7)

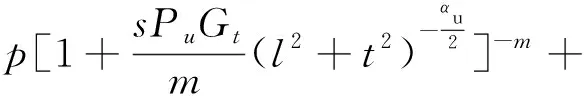
(8)

證明：

D2D用戶的成功傳輸概率Pcov,d(θ)可以表示為

Pcov,d(θ)=P(SIRD2D>θ)

(9)

其中信道增益h服從指數分布，則

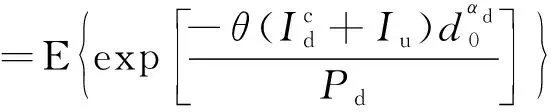
(10)

根據拉普拉斯變換，可推導出

(11)

(12)

令σd=2/αd，關于式(11)的推導，本文中可直接使用文獻[15]的結果,即

(13)

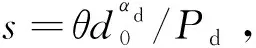
LIu(s)=EIu[exp(-sIu)]

(14)

式(14)中：步驟(a)是根據伽馬函數的矩量母函數(moment generating function, MGF)獲得；步驟(b)是因為變量t以及Gj是相互獨立的隨機變量；步驟(c)是由HPPP的概率生成函數(probability generating functional，PGFL)得到的結果，其中

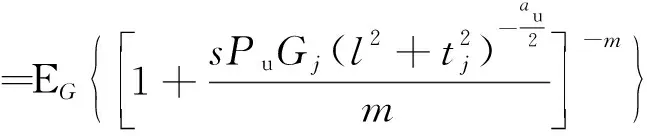
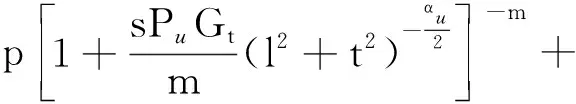
(15)

2.2 下行鏈路用戶的成功傳輸概率

在無人機與下行鏈路用戶通信過程中，空對地信道使用的是Nakagami衰落信道模型，求取精確的下行鏈路用戶成功傳輸概率表達式涉及較高的計算復雜度。為了簡化分析，本文中通過求取下行鏈路用戶成功傳輸概率的上下界理論表達式來近似評估其性能。

定理2令q=1-p,σd=2/αd,σu=αu/2,α=(m!)-1/m,η(r)=αθ(l2+r2)σu/PuGt，則下行鏈路用戶成功傳輸概率的上界表達式為

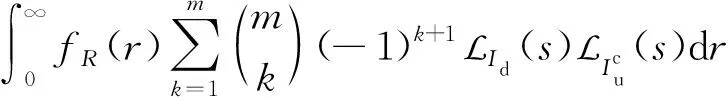
(16)

s=η(r)mk，fR(r)=e-λuπr2×2πλur

(17)

(18)

(19)

τ(s,t)=p[1+sPuGt(l2+t2)-σu]-m+

q[1+sPugt(l2+t2)-σu]-m

(20)

當η(r)中的α=1時，式(16)為下行鏈路用戶成功傳輸概率的下界表達式。

證明：

由于無人機的分布是服從PPP的，在不失一般性的情況下，考慮一個位于原點的典型下行鏈路用戶。該下行鏈路用戶與其服務無人機之間的距離為X0=(l2+R2)1/2，其中R為服務無人機在地面的投影到該下行鏈路用戶之間的距離，其分布服從二維PPP，概率密度函數為式(17)，因此，該下行鏈路用戶的成功傳輸概率可以表示為

Pcov,du(θ)=ER[P(SIR>θ|r)]

(21)

P(SIR>θ|r)

(22)

由于下行用戶與無人機通信的小尺度衰落被建模為參數為m的Nakagami衰落，其信道增益C服從Gamma分布，因此，信道增益C的CCDF為

FC(x)=Γ(m,xm)/Γ(m)

(23)

即式(22)可以推導為

P(SIR>θ|r)=1-

(24)

從文獻[16]可知，當m≠1，以及

知伽馬分布存在關系式

[1-exp(-αmg)]m

(25)

由不等關系以及二項式定理，式(24)可以推導為

P(SIR>θ|r)

(26)

EId{exp[-η(r)mkId]}

(27)

根據拉普拉斯變換，可推導如下

LId[η(r)mk]=EId{exp[-η(r)mkId]}

(28)

(29)

令s=η(r)mk，σd=2/αd，由文獻[15]可知

LId(s)=EId[exp(-sId)]

(30)

式(29)可以推導為

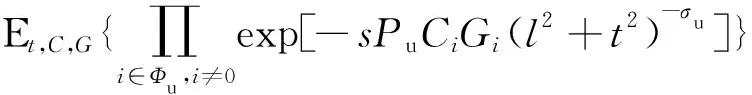
(31)

式(31)中：步驟(a)使用了Gamma函數的MGF；步驟(b)是根據齊次泊松點過程的PGFL得到的結果，積分下限為R是因為最近的干擾無人機在地面的投影在距離R外。最后，τ(s,t)推導如下：

τ(s,t)=EG{[1+sPuGi(l2+t2)-σu]-m}

=p[1+sPuGt(l2+t2)-σu]-m+

q[1+sPugt(l2+t2)-σu]-m

(32)

類似地，根據式(27)的左不等式，令η(r)中的α=1，則可得到下行鏈路用戶成功傳輸概率的下界。

2.3 系統和速率

系統內D2D通信用戶以及下行鏈路用戶的平均可達速率[14]可以被分別表示為

Cd=Wlog2(1+θ)Pcov,d(θ)

(33)

Cdu=Wlog2(1+θ)Pcov,du(θ)

(34)

式中：W為系統帶寬，分別將D2D用戶以及下行鏈路用戶的成功傳輸概率代入即可得到式(33)以及式(34)的具體表達式。考慮到目標區域內所有的通信用戶，系統和速率可以被推導為關于用戶成功傳輸概率以及用戶數量的函數，即

(35)

3 仿真驗證

現給出無人機與D2D通信共存網絡下兩種不同類型通信用戶的成功傳輸概率數值仿真結果。其中，數值結果通過理論公式得出，仿真結果基于蒙特卡羅方法[17]，通過106次仿真實現得到。以系統和速率作為性能指標，分析無人機高度、無人機密度以及定向天線陣列參數對網絡性能的影響。系統默認仿真參數為Rc=1 000 m，λu=10-4個/m2，λd=10-3個/m2，λdu=10-3個/m2，Pu=10 W，Pd=0.1 W，d0=1 m，l=100 m，W=100 MHz，αu=3，αd=4.5，m=4，N=4。

圖2所示為不同D2D用戶密度下，SIR檢測閾值與D2D用戶成功傳輸概率之間的關系。由圖2可以得出以下結論。

圖2 不同SIR閾值的D2D用戶成功傳輸概率Fig.2 The successful transmission probability of D2D users with different SIR thresholds

(1)理論和仿真結果十分匹配，驗證了定理1的準確性。

(2)D2D用戶的成功傳輸概率隨著SIR閾值的增加而下降得越來越快，這說明選擇合適的SIR閾值對提高D2D用戶的成功傳輸概率至關重要。而SIR閾值往往與編碼調制方式有關。

(3)在相同的SIR閾值下，D2D用戶的成功傳輸概率隨著D2D用戶密度的增加而下降。這說明在服務質量要求不同的地區，可以通過不同的D2D模式選擇以及資源分配方案來控制D2D用戶的密度，以實現對系統內資源的最大利用。比如當SIR閾值θ=-10 dB時，D2D用戶的成功傳輸概率都接近為1，說明對服務質量要求較低的地區，可以讓更多的用戶通過D2D通信的方式來滿足通信需求，減少無人機基站的部署以及成本投入。而當SIR閾值θ=20 dB時，D2D通信用戶過多則無法保證數據的成功傳輸，需要增加無人機基站的部署。

圖3給出了不同SIR檢測閾值下，下行鏈路用戶成功傳輸概率的理論值上下界與仿真結果的對比，從圖3可以看出，實際仿真結果與理論分析表達式的上界更加接近，也就是說，在定理2給出的理論公式中，下行鏈路用戶成功傳輸概率的上界給實際的成功傳輸概率提供了較好的近似效果，分析下行鏈路用戶的成功傳輸概率時可以將理論值上界作為性能參考指標。

圖4所示為不同的無人機密度下天線參數對系統和速率的影響。給定SIR閾值θ=0，無人機高度l=30 m，其中N=1表示全向天線。從圖4中可以得出以下結論。

(1)系統和速率首先隨著無人機密度的增加而快速增大，這是因為隨著無人機密度的增加，下行鏈路用戶距離其服務無人機越來越近，收到的有用信號越來越強，使得系統和速率隨之提升。而隨著無人機密度的繼續增加，無人機對D2D用戶的干擾越來越大，當對D2D用戶的干擾功率增大量超過了對下行鏈路用戶的有用功率增大量，系統的和速率就會開始下降。因此，存在一個最優的無人機密度使得系統的和速率最大。

圖3 不同SIR閾值的下行鏈路用戶成功傳輸概率Fig.3 The successful transmission probability of downlink users with different SIR thresholds

圖4 無人機密度對系統和速率的影響Fig.4 The impact of the height of UAVs on the system sum-rate

(2) 相比全向天線，給無人機配備定向天線有效地提高了系統性能。比如，當無人機配備全向天線時，系統和速率最大為4.2×1011bit/s，給無人機配備定向天線陣列后，系統和速率得到了明顯提升，其中天線陣子數N=4時的系統最大和速率為5.49×1011bit/s，相比全向天線提升了30.7%，且天線陣子數越多，系統和速率性能越好。但無人機能夠配置的陣列天線大小同時取決于天線材料、信號頻率、無人機承載能力等約束，并不能無限制增加，具體的陣列天線大小需參考不同地區的用戶數量以及網絡服務需求。

系統和速率與無人機高度之間的關系如圖5所示。從圖5中可以得出以下結論。

(1)通過分析系統內D2D用戶以及下行鏈路用戶成功傳輸概率可知，無人機高度越大，對D2D用戶干擾越小，D2D用戶成功傳輸概率越大，但同時無人機通信用戶距離其服務基站越來越遠，導致無人機通信用戶的成功傳輸概率越來越小。而系統和速率是關于D2D用戶以及下行鏈路用戶成功傳輸概率的函數，所以從圖5中不難發現，系統和速率隨著無人機高度的增加呈緩慢上升后下降的趨勢，即存在一個最優的無人機高度使系統和速率達到最大。

(2)由于本文不考慮障礙物遮擋的情況，即無人機在LOS條件下與下行鏈路用戶進行通信，所以根據無人機配備天線類型以及陣列天線大小的不同，無人機的最優高度區間為[20,30]m。如果需要無人機懸停在距離地面更遠的高度上，需要給無人機配備定向天線陣列并增加天線陣子的數量。比如，當無人機高度為100 m時，N=8時的系統和速率比N=4時每秒鐘提高1.1×1011bit。因此，針對不同的網絡服務需求，可以考慮給無人機配置不同大小的陣列天線。

圖5 無人機高度對系統和速率的影響Fig.5 The impact of the density of UAVs on the system sum-rate

4 結論

基于隨機幾何理論，提出了一種配備定向天線陣列的無人機充當空中基站，采用波束通信方式為地面用戶提供服務，且與D2D通信共存的網絡模型。推導了該模型下D2D用戶的成功傳輸概率表達式以及下行鏈路用戶的成功傳輸概率上下界理論表達式，并通過蒙特卡羅方法進行了仿真驗證。此外，分析不同的網絡參數對系統性能的影響，得出以下結論。

(1)在其他參數不變的條件下，存在最優的無人機高度以及無人機密度使系統和速率達到最大。

(2)相比全向天線，給無人機配備定向天線陣列提高了30%以上的系統和速率，有效地提高了系統的通信性能。同時，針對服務質量要求較高的地區，可以考慮給定向天線陣列裝配更多的天線陣子。

然而，目前的基于隨機幾何的無人機網絡研究中較少涉及用戶到無人機上行鏈路性能特性分析。下一步將增加網絡中的上行鏈路性能分析，比較不同參數對系統性能的影響。