考慮級配參數空間變異性的堆石壩隨機有限元分析

陸雪妮，朱 晟

(河海大學水利水電學院，江蘇 南京 210024)

0 引 言

堆石壩工程中堆石料的級配變動會在很大程度上影響材料的物理力學性質，進而影響壩體的變形應力。已有研究表明，堆石料的物理力學特性與其級配分布緊密相關，李罡等[1]通過數值試驗和室內試驗研究，發現顆粒級配對材料應力應變關系的影響顯著；趙婷婷等[2]基于顆粒流試驗，發現表征顆粒級配分布的分形維數與堆石料的力學特性存在明顯相關關系，可將分形維數用于量化分析堆石料的力學特性；加力別克等[3]根據一系列室內三軸壓縮試驗結果，整理了分形維數與鄧肯E-B模型參數之間存在的二次函數關系。由此可見，堆石料的級配參數作為表征材料分布的重要參數，在堆石壩有限元計算中應當加以考慮，不可忽視堆石料級配效應對壩體力學響應的影響。朱晟等[4]結合不同級配堆石料的三軸試驗結果，分析了堆石料級配參數與各力學特性之間的關系，基于廣義塑性模型理論，建立了本構模型參數與分形維數之間的函數關系式，并驗證了合理性，從而為考慮級配效應的有限元計算提供了有效途徑。

目前，傳統的確定性有限元計算方法對于大壩各分區材料均采用單一級配的假定，沒有考慮到堆石料級配參數的空間變異性。即使是同一分區的堆石料，由于受到自然條件、母巖性質、填筑過程等多種因素影響，其級配參數也會存在分布上的空間變異性，這種空間變異性是與位置和距離緊密相關的。因此，為了可以更好地反映工程實際，可在考慮級配效應的有限元計算基礎上，引入隨機場理論和相關離散方法，用隨機場的統計特性對堆石料級配參數的空間變異性進行表征，建立堆石料級配參數的三維隨機場模型，結合考慮級配效應的堆石壩有限元分析方法對壩體力學響應進行研究。

本文以某抽水蓄能電站面板堆石壩作為工程實例，對堆石壩進行有限元網格剖分，整理統計堆石料的級配參數和靜力計算本構模型參數，采用Cholesky分解法建立堆石料級配參數的三維空間隨機場模型，結合考慮級配效應的堆石壩有限元分析方法，通過多次隨機模擬，對隨機計算結果進行統計分析，討論堆石料級配參數的空間變異性對堆石壩變形安全的影響。

1 對數正態隨機場模擬方法

已有眾多學者[5-11]對堆石料材料參數隨機場模型的建立展開研究，考慮到對數正態隨機場在對數值大于零的模型參數進行模擬時的良好效果，研究中將筑壩堆石料材料參數均擬定為服從對數正態分布的隨機變量。本文采用對數正態隨機場對堆石料級配的分形維數進行隨機模擬。

在隨機場模型中，一般采用理論自相關函數來描述堆石料同一分區中兩個不同空間位置處參數之間的自相關性[12]，由于高斯型自相關函數具有較好的平穩性，本文選用高斯型自相關函數進行表征，即

(1)

(2)

式中，δx、δy、δz分別為3個坐標方向上的波動范圍；θx、θy、θz分別為3個坐標方向上的相關距離；τx=|xi-xj|，τy=|yi-yj|和τz=|zi-zj|為任意2個空間位置點之間的平行于坐標方向的間距。

對數正態隨機場模擬方法的具體步驟為：

(1)根據有限元計算網格將隨機場離散劃分成一系列單元，令隨機場單元與有限元單元一致，計算各單元中心點坐標(xi，yi，zi)，i=1， 2，…，ne，ne為隨機場研究域內的單元數量。

(2)采用拉丁超立方抽樣(LHS)方法隨機生成獨立標準正態空間隨機向量ξ(ξ為含ne個隨機抽樣點的列向量)，經過m次隨機抽樣(m為隨機模擬次數)，可以得到m個列向量。

(3)將步驟(1)得到的各單元中心點坐標代入式(1)，計算得到空間任意兩點之間的自相關系數，構成自相關系數矩陣

(3)

當堆石料級配參數原始隨機場為對數正態隨機場時，需要將原始自相關矩陣C等概率轉換成相應的標準正態空間的等效自相關系數C0，計算公式為

(4)

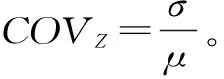
(4)采用Cholesky分解方法對上一步得到的等效自相關矩陣C0進行分解，得到下三角矩陣L(ne×ne)，乘上步驟(2)得到的獨立標準正態隨機向量樣本ξ，即能夠求得標準參數高斯隨機場

(5)

然后結合均值μ、標準差σ等概率分布統計特征值，進行等概率變換，將上述得到的標準參數高斯隨機場轉換成相應的對數正態隨機場，具體變換公式為

圖1 大壩典型剖面示意

(6)

(5)以上過程實現了一次對數正態隨機場的建立，對于步驟(2)中的m次隨機抽樣結果，將步驟(3)～步驟(4)進行m次重復，即實現了對數正態隨機場的m次模擬與建立。

2 工程實例

2.1 單元網格剖分與荷載分級

根據所研究堆石壩工程的壩址地形及壩體分區資料，圖1為大壩分區示意，模擬大壩填筑施工過程，逐級施加荷載，共分32級模擬大壩填筑過程，建立大壩三維有限元計算網格模型，如圖2所示，共剖分網格節點59 298個，總單元57 359個，壩體底部施加固定約束。

圖2 堆石壩有限元網格模型

2.2 堆石料級配參數空間隨機場模擬

采用分形分布模型[13]擬合主堆石區、下游堆石區等主要分區壩料的顆粒級配曲線。對于堆石料，顆粒質量的分形分布模型為

(9)

式中，P(di)為小于di的顆粒質量分數；di為顆粒直徑；dmax為最大粒徑；D為分形維數。

結合施工填筑檢測級配資料，其中主堆石料的實測級配數據共計147組，下游堆石料級配數據共計99組，擬合各分區壩料的顆粒級配曲線，如圖3所示，相關系數均大于0.95，認為堆石料級配基本滿足分形分布。

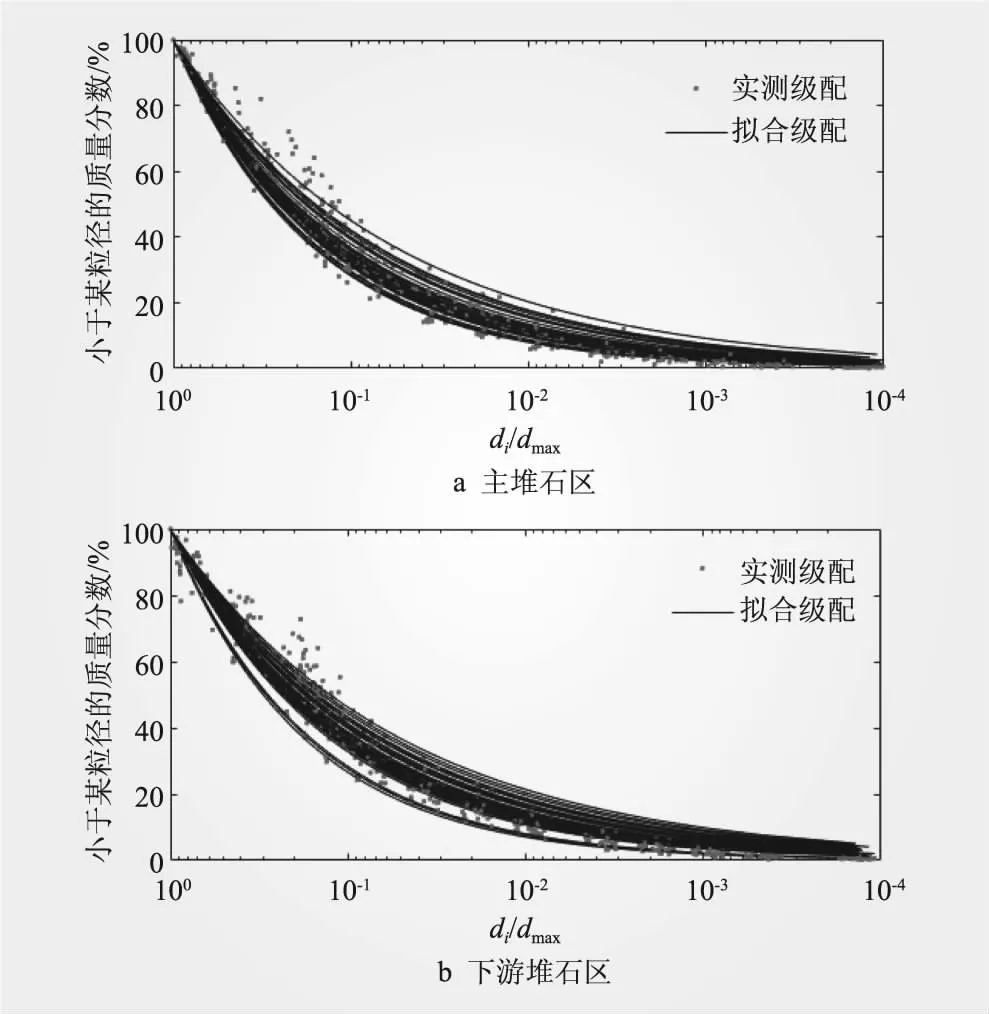
圖3 堆石料填筑級配曲線

繪制分形維數的頻率分布直方圖和對數正態概率分布圖，如圖4、5所示，正態概率圖用于檢查一組數據是否服從正態分布，對主堆石區和下游堆石區的分形維數D取對數后繪制正態概率分布圖，發現散點近似呈一條直線，說明主堆石區和下游堆石區的分形維數D滿足對數正態分布。對各區分形維數D進行統計分析，根據3σ準則對各區分形維數D中含粗大誤差的數據予以剔除，得到的各區參數分布范圍為主堆石區2.34～2.71，下游堆石區2.44～2.71，見表1。

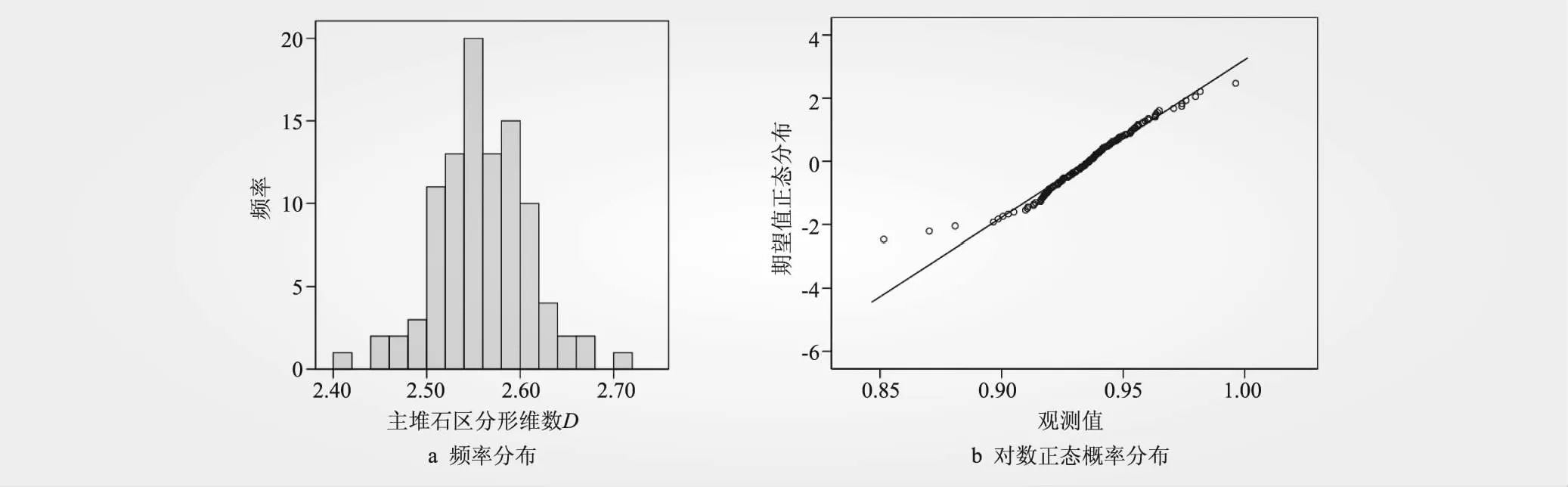
圖4 主堆石區分形維數D概率統計規律

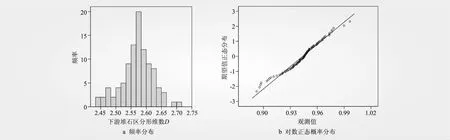
圖5 下游堆石區分形維數D概率統計規律

表1 各區級配分形維數分布統計分析

表2 堆石料分形維數隨機場的數字特征

在確定隨機場特征值的基礎上，根據前文所述對數正態隨機場模擬方法，分別對主堆石區和下游堆石區的分形維數D進行隨機模擬，采用中點映射法將各分區隨機場中的分形維數D賦值給對應的壩體有限元網格單元，即可得出壩體堆石料分形維數的三維隨機場。本文對堆石料分形維數隨機場進行了200次隨機模擬，根據其中一次隨機模擬得到的堆石料分形維數D的三維隨機場，繪制堆石料三維整體和最大斷面的分形維數D的空間分布云圖，如圖6所示，發現主堆石區和下游堆石區的分形維數值分布沒有明顯的分界，主要原因是兩個分區分形維數的統計特征值之間差異不大，且變異系數均較小。在建立三維隨機場模型后，即可利用隨機場模型中的分形維數值進行壩體有限元計算。

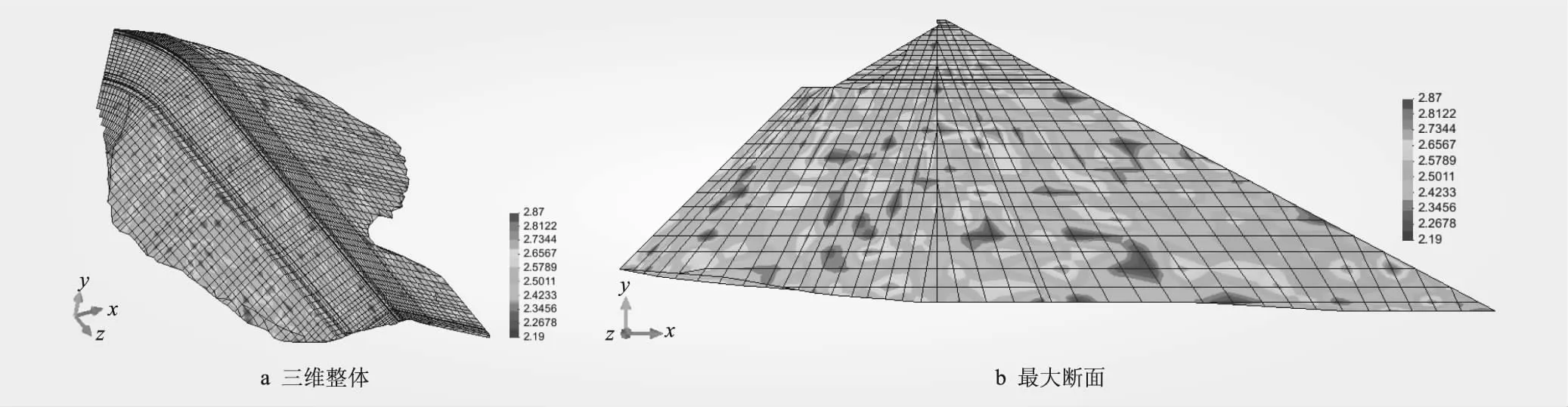
圖6 主堆石區和下游堆石區的分形維數D的空間分布云圖

圖7 竣工期典型斷面應力變形分布云圖(單位：位移cm；應力MPa)

2.3 靜力計算本構模型參數

計算采用可以反映堆石料剪脹性的統一廣義塑性模型[16]。考慮級配效應對大壩有限元計算的影響，需要研究筑壩料級配參數與其力學特性之間的關系。已有研究[4]以大量堆石壩工程的試驗結果為依據，分析了表征抗剪強度、剪脹性、壓縮性等特性的參數與級配參數之間的關系，其建立的廣義塑性模型參數與分形維數之間的函數關系式可將級配參數直接應用于堆石壩有限元計算中。本文主要研究考慮堆石料級配參數空間變異性時壩體的結構響應，因此對于庫盆回填區、過渡區、墊層區等體積較小、對大壩主體影響較小的分區筑壩料，堆石料的分形維數按照單一級配的假定作均一化處理，僅探究對壩體變形應力影響較大的主堆石區和下游堆石區的分形維數隨機分布。

對于主堆石區、下游堆石區的堆石料，需要考慮級配參數的空間變異性，對主堆石區、下游堆石區的堆石料級配參數隨機場進行離散，實現足夠多次數的對數正態隨機場的模擬與建立，然后根據單元中心點的坐標，將所建隨機場模型中的分形維數值一一映射到相應位置的網格單元中，根據分形維數與廣義塑性模型參數之間對應的函數關系式[4]，完成堆石料單元級配參數與本構模型參數之間的映射，從而直接將級配參數直接應用于壩體有限元計算中。

2.4 考慮級配參數空間變異性的堆石壩三維有限元應力變形分析

以與圖6隨機場對應的隨機有限元計算結果作為典型案例，選取壩體最大斷面作為典型斷面，整理竣工期堆石壩應力變形隨機響應結果，如圖7所示。圖7中，位移豎直向上為正，豎直向下為負；水平位移向下游為正，向上游為負；壓應力為正，拉應力為負。

由圖7a可知，壩體沉降分布規律符合一般規律，壩體沉降較顯著的位置主要集中于主堆石區、下游堆石區以及二者交界處。隨機性有限元方法算得的竣工期壩體最大豎直沉降量為98.5 cm，位于下游次堆石區183.7 m高程附近，約1/2壩高處。

由圖7b可知，壩體的水平向位移基本上主要指向下游，這主要是受到了向下游傾斜的壩基地形和堆石體的泊松效應兩方面的影響。隨機性有限元方法計算得到竣工期的水平向位移最大值為16.3 cm，指向下游方向，位于下游次堆石區的170.0 m高程附近。

由圖7c、7d可知，竣工期的堆石壩大、小主應力的等值線分布均呈現出和壩坡近似平行的趨勢，并且應力值隨高程自上而下逐漸增大，在壩基處達到最大值。隨機性有限元方法算得壩體大主應力最大值為2.92 MPa，位于主堆石區底部地基處；小主應力最大值為1.40 MPa，也位于主堆石區底部位置。

圖8 隨機有限元計算結果的統計穩定性(竣工期)

3 隨機有限元計算結果分析

3.1 計算結果的統計穩定性

對壩體主堆石區和下游堆石區堆石料的分形維數分別進行200次隨機模擬后，完成相應的隨機有限元計算，在對200次隨機有限元計算結果進行統計分析前，需要先判斷經過多次隨機模擬后的輸出結果是否達到統計穩定狀態。通過繪制隨機計算結果的滑動平均值以及滑動標準差隨模擬次數的波動曲線，作為判斷隨機模擬是否穩定的依據，若曲線波動性減弱、波動趨于平穩，則判定隨機模擬計算結果達到穩定狀態，認為隨機模擬次數已足夠。

滑動平均值Runava(n)和滑動標準差Runsd(n)分別定義為

(10)

(11)

根據以上計算公式，將竣工期壩體豎直沉降、水平向位移、大主應力及小主應力等變形應力指標的最大值作為壩體響應值，繪制各響應值的滑動平均值Runava和滑動標準差Runsd隨模擬次數變化的波動示意圖，如圖8所示。可以發現當隨機模擬次數達到60次時，各響應值的波動曲線波動性均已減弱，曲線趨于平穩，當模擬次數達到140次以上曲線波動性已經非常穩定，認為曲線達到收斂狀態。因此對壩體實現200次隨機場模擬，認為隨機模擬次數滿足穩定要求，由此得到的統計分析結果足以很好地代表總體的統計特性。

3.2 統計分析

對200次隨機有限元計算結果進行統計分析，統計特性如表3所示，由均值和標準差計算得到各響應值的變異系數分別為1.60%、1.56%、3.27%、1.85%、2.52%，各響應值的概率分布情況如圖9、10所示。對壩體各隨機響應值分別繪制正態概率分布圖，用于檢驗是否服從正態分布，如圖9、10所示，各響應值的正態概率分布圖上的點可以較好地用直線擬合，認為滿足正態分布，由此表明，堆石料級配的分形維數滿足對數正態分布時，壩體應力變形基本滿足正態分布。

3.3 與確定性有限元比較

如果不考慮堆石料級配參數的空間變異性，大壩各分區按照單一級配計算，即主堆石區、下游堆石區的分形維數取其平均值計算，作為確定性有限元計算結果，列于表4中。根據各壩體響應值的均值表征隨機性有限元的計算結果，計算得到竣工期最大豎直沉降為97.8 cm，比確定性有限元方法算得的最大豎直沉降95.1 cm多出2.84%；最大水平向位移為16.3 cm，比確定性有限元方法算得的最大水平向位移16.0 cm多出1.88%；大主應力最大值為2.98 MPa，比確定性有限元方法算得的大主應力最大值2.85 MPa多出4.56%；小主應力最大值為1.43 MPa，比確定性有限元方法算得的小主應力最大值1.34 MPa多出6.72%。根據表4的計算結果比較情況可以看到，與忽略級配參數空間變異性的確定性有限元相比，隨機性有限元的變形和應力均偏大，計算結果偏于安全，兩者相對誤差在2%～7%左右，由此可見，如果不考慮堆石料級配參數的空間變異性，很可能會在一定程度上低估壩體變形和應力。

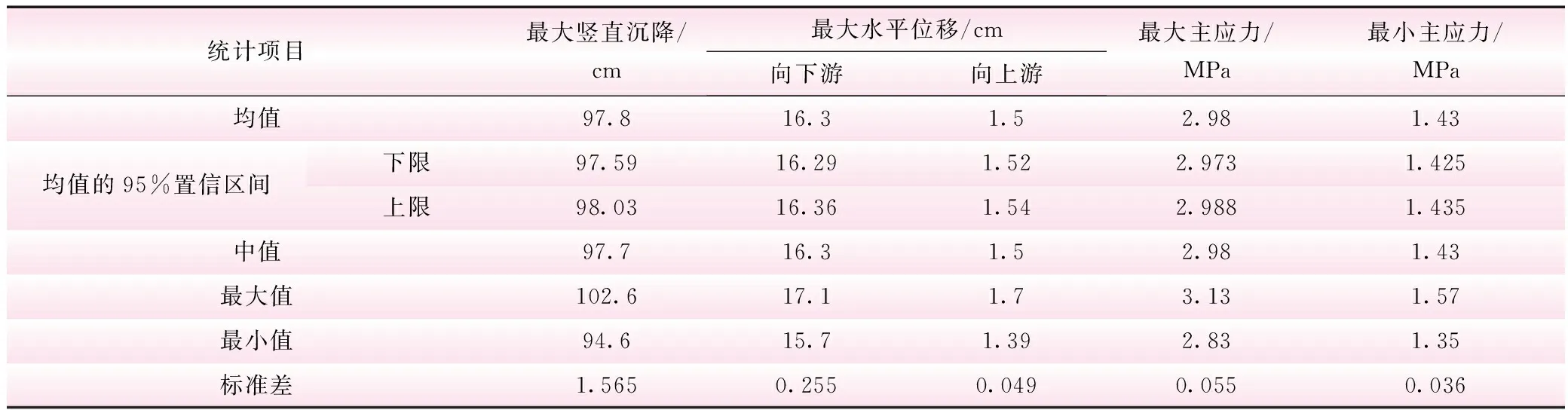
表3 壩體200次隨機模擬響應值的統計特性(竣工期)

圖9 竣工期壩體變形概率統計規律

圖10 竣工期壩體應力概率統計規律

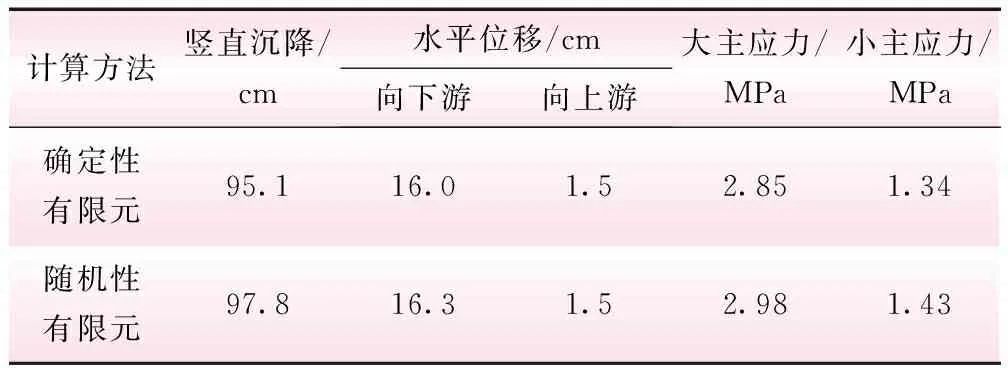
表4 考慮級配參數空間變異性的隨機有限元計算結果與確定性有限元對比(竣工期)

4 結 論

本文以某面板堆石壩工程為例，發展了基于Cholesky分解的堆石壩隨機有限元計算方法，建立堆石料級配參數的三維隨機場模型，結合考慮級配效應的堆石壩有限元分析方法對壩體力學響應進行研究，主要結論如下：

(1)堆石料級配曲線基本滿足分形分布模型，分形維數D可較好地表征級配曲線，主堆石區、下游堆石區等分區的分形維數頻率分布近似服從對數正態分布。

(2)基于Cholesky分解法實現堆石料分形維數的對數正態隨機場模擬，并將隨機參數映射至有限元分析模塊，計算考慮級配參數空間變異性時的壩體結構響應分析。計算結果表明：當隨機模擬至200次時，壩體各響應值達到統計穩定，且堆石料級配的分形維數滿足對數正態分布時，算出的壩體應力變形基本滿足正態分布。

(3)與壩料各分區參數采用單一級配假定的確定性有限元相比，隨機性有限元的變形和應力均偏大，計算結果偏于安全，兩者相對誤差在2%～7%左右。如果不考慮堆石料級配參數的空間變異性，會在一定程度上低估壩體變形和應力。