基于全信息初值優化的GM(1,1)模型在物流行業中的應用

□ 嚴亞波

(江南大學 商學院,江蘇 無錫 214122)

1 引言

灰色系統理論[1]自1982年問世以來，就因在研究“小數據”“貧信息”等不確定性問題時具有優勢而廣受關注。灰色預測模型理論是研究最活躍、應用最廣泛的灰色系統模型之一，灰色預測是一種時間序列預測方法，該方法的優勢在于建模數據量小，建模過程簡單，因而被廣泛研究。其中，GM(1,1)模型是灰色預測理論中最核心的模型，是灰色模型中的基礎，也是被研究次數最多、應用最廣泛的灰色預測模型，并衍生出諸多變種。學者們從應用以及優化等多個方向對GM(1,1)模型進行了深入研究。

近年來，GM(1,1)模型在諸多領域得到了廣泛的應用。盧捷、李峰將初始值和背景值看作變量，對經典GM(1,1)模型背景值與初始值進行改進,提出了一種初始值和背景值組合優化的方法[1]；羅黨、王小雷在灰色預測模型中引入三角函數，由此提出了耦合結構的灰色GM(1,1,T)模型，然后利用Levenberg-Marquardt算法求解模型結果[2]；劉震、謝玉梅、黨耀國建立脫貧攻堅理論模型,分析政策性扶貧的外生性影響，而后依據脫貧規律對GM(1,1)模型進行改進,構建脫貧進展預測模型[3]；亢玉曉、肖新平研究GM(1,1)多種不同衍生模型的缺陷，并對其差異性進行分析[4]；呂海濤、程帥帥、吳利豐等基于殘差尾段的強(弱)化緩沖算子還原模型，拓展了模型的建模應用范圍[5]；張福平、劉興凱、王凱建立研究生規模的灰色模型對畢業人數、招生數以及在校學生數規模進行預測[6]；李翀、謝秀萍考慮系統時滯的動態變化效應，提出以灰色關聯理論為基礎的時變時滯函數的參數優化方法[7]；李麗、李西燦定義了背景值系數序列，并推導了GM(1,1)灰微分方程的解的表達式，然后利用優化算法求解準光滑數列的最佳背景值系數，來提高GM(1,1)模型的精度[8]；丁松等通過對原始序列加權，在考慮新信息優先的基礎上優化初始條件，構建了全信息初始條件優化的非等間距GM(1,1)模型[9]；江藝羨、張岐山利用黎曼積分推導出了以不規則梯形面積取代傳統梯形面積構造法，以此優化了傳統GM(1,1)模型背景值[10]；Xiao X P、Guo H、Mao S H運用矩陣分析思想對GM(1,1)模型的建模機理進行分析，提出了基于分數階累積生成的GGM(1,1)模型的可拓形式，分析了其理論意義[11]；Ceylan Z、Bulkan S、Elevli S對自回歸綜合移動平均法(ARIMA)、支持向量回歸法(SVR)、灰色建模法(1,1)和線性回歸法(LR)等各種數學建模方法在預測土耳其最大城市伊斯坦布爾醫療廢物產生方面的效果進行評估[12]；Shen Q Q等基于新的信息優先級原則和分數累積生成算子的思想，提出了一種新的加權分數GM(1,1) (WFGM(1,1))預測模型[13]；Wang Q、Song X提出NMGM (1,1,alpha)，通過有效地結合非線性預測技術和生物代謝思想，將非線性灰色模型(GM)從靜態模型升級為動態模型，并預測中國石油消費[14]；Zeng B、Li C提出了一種自適應智能灰色預測模型，與傳統灰色模型結構固定、適應性差的缺點相比，該模型可以根據建模序列的真實數據特征自動優化模型參數[15]；Wang Y等通過對原始序列第一個分量和最后一個分量進行加權來優化初始條件以提高GM(1,1)模型預測精度的新方法，利用最小誤差平方和法求解組合中第一項和最后一項作為初始條件的加權系數[16]；Lu Y、Xie N、Wei B等提出了一個統一的框架，從積分-微分方程的角度重建了統一的非線性灰色系統模型，并將該模型應用于長三角城市污水排放和用水量預測中[17]；Tong M Y從傳統GM(1,1)模型的背景值入手，采用外推法對模型進行擴展，提出了一種優化的灰色預測模型，采用模擬退火算法求解模型[18]；Zeng Bo等對物理指標的數據特征進行了系統的分析，應用具有這些特征的數據專用的灰色系統模型，對人體指標的變化趨勢進行了模擬和預測[19]；丁松等按照信息充分利用以及新信息優先等原理對模型初始條件進行優化，然后提出了一種初始條件和冪指數組合優化的方法[20]。

通過對以往文獻的分析研究，可以發現傳統GM(1,1)模型的初始條件為序列的第一個分量x(1)(1)[21]，但是初始序列距離系統較遠，影響有限，而對系統影響較大的新信息的作用卻常常被忽略，因此存在一定誤差；此外，也有專家學者基于新信息有限選擇最后一個分量x(1)(n)作為初始條件[22]，雖然在一定程度上利用了新信息，但只考慮新信息對系統的影響而忽略舊信息的作用，同樣會影響模型精度；還有部分學者選擇以二者線性組合來優化初始條件，然后利用算法等進行求解[20]，該方法雖然由舊信息和新信息組合來優化，但沒有充分考慮不同信息對系統的影響程度不同，對于“數據量小”的灰色預測模型來說，勢必不能夠對有效信息進行充分提取，造成信息的浪費，從而影響GM(1,1)模型建模效果。本文對模型的改進也將從這個角度展開。

文獻[20]根據新信息優先原理，對原始數據的每一個量進行加權優化初始條件，通過設置權重系數來表現新舊信息在初始條件構建中作用大小的變化規律，以充分提取原始序列中對系統發展預測有效的信息，充分利用舊數據的經驗知識和新數據的趨勢信息，綜合考慮新舊信息間的權重分配關系，來構建新的初始條件。本文在文獻[20]的基礎上，將該初值優化方法引入到GM(1,1)模型優化中，構建了基于初始條件優化的GM(1,1)模型，并利用該模型對我國物流行業發展規模進行預測。

2 GM(1,1)模型的基本形式

GM(1,1)模型是灰色系統中最基礎的模型，同時也是最重要且應用范圍最廣的模型。GM(1,1)模型中第一個“1”意為一階方程，第二個“1”意為單變量。本節將重點介紹傳統GM(1,1)模型的建模機理。

設非負原始序列為X(0)=(x(0)(1),x(0)(2),…,x(0)(n))，對原始序列X(0)作一階累加生成(1-AGO),得到序列：

X(1)=(x(1)(1),x(1)(2),…,x(1)(n))

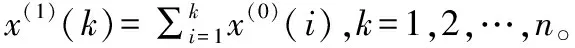
對序列X(1)作緊鄰均值生成，得到序列：

Z(1)=(z(1)(2),z(1)(3),…,z(1)(n))

其中，z(1)(k)=0.5(x(1)(k)+x(1)(k-1)),k=2,3,…,n。

定義2.1：設X(0)為非負原始數據序列，X(1)為X(0)的1-AGO序列，Z(1)為X(1)緊鄰均值生成序列，則有稱

x(0)(k)+ax(1)(k)=b

(1)

為原始GM(1,1)模型，

x(0)(k)+az(1)(k)=b

(2)

為具有背景值的GM(1,1)模型。

定義2.2：設a為發展系數，b為灰作用量，則稱

(3)

為GM(1,1)模型的白化方程。

(1)白化方程的時間響應函數表達式為

(4)

(2)在初始條件x(1)(t)|t=1=x(1)(1)時的時間響應式為

(5)

(3)還原值為

(6)

上述為傳統GM(1,1)模型的建模機理，由于該模型應用十分廣泛，由此可以演化出多種不同的GM(1,1)模型，如EGM(1,1)模型、DGM(1,1)模型、SGM(1,1)模型等。傳統模型雖然應用廣泛，但仍有較大改進空間。

3 優化的GM(1,1)模型構建及參數求解

為了對系統有效信息進行充分提取，提高建模精確度，本節將采用全新的方法對GM(1,1)模型初始條件進行優化，并研究相關參數的求解路徑。

3.1 基于全信息初值優化的GM(1,1)模型

在實際建模過程中，GM(1,1)模型的預測精度不該只和原始序列的第一個分量x(1)(1)或者最后一個分量x(1)(n)有關，而是與X(1)的每一個分量都存在一定的關系。新信息優先原理提出，新信息對系統發展趨勢變化的影響更大，因而在建模過程中對系統未來發展的預測作用遠大于離系統較遠的舊信息，所以在初值構建過程中新信息應當被賦予更大的權重。但這并不意味著舊信息就應當被摒棄，盡管舊信息的預測效用較低，但依據信息充分利用原理，舊信息也不應被摒棄，而是充分利用其中殘存的有用信息來進一步提高模型精度。因此，在建模過程中要對新舊信息進行權重分配使得權重能夠準確反映信息對初始條件的實際影響大小，能夠有效地提高灰色預測模型的建模精度。因此，在充分考慮新舊信息的預測效用的情況下，引入一個權重系數λn+1-k(0<λ<1)，k=1,2,…,n，以X(1)的所有分量的加權組合來構建初始條件，從而對灰色GM(1,1)模型進行優化，即以

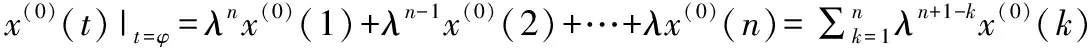
(7)

為初始條件。權重λn+1-k(0<λ<1),k=1,2,…,n將隨著時間的推移而遞減，分量越靠后則權重越大，且其遞減速度與λ取值相關，λ取值越小，遞減越快，反之越慢，如圖1所示，圖中橫坐標表示λn+1-k隨著冪指數增加而變化，在λ的不同取值下，λn+1-k變化情況如圖所示。λn+1-k一定程度上揭示了原始序列的每個分量作用隨著時間的推移在不斷增加。權重系數的選擇主要由數據序列的實際意義所決定，而非人為設定。從圖1可以看出，λk-1<λk-2<…<λk+1-n滿足序列的權重隨著信息的新舊程度由舊到新不斷增加，且序列的所有分量對系統的影響實際效用均被考慮到，構建的新初值既滿足新信息優先原理又滿足信息充分利用原理。

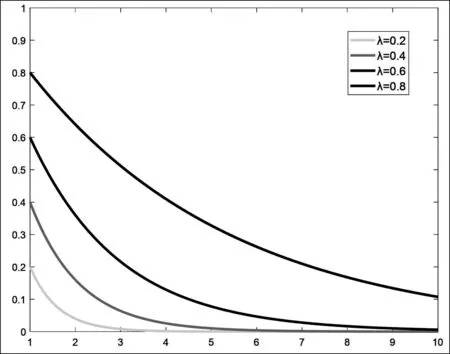
圖1 不同λ取值對應權重系數變化趨勢

(8)

(9)

(2)還原值為

(10)

如此便得到基于全信息初值優化的GM(1,1)模型，記為PIGM(1,1,λ)。

3.2 基于全信息初值優化的模型參數求解

通過基于初值優化的GM(1,1)模型的建模機理可知，我們只要確定了初值參數φ，便可實現基于初值優化的GM(1,1)模型模擬和預測，因此，對于初值參數φ的求解是至關重要的一步。本節將通過建立非線性優化模型，借助matlab軟件，求解模型的最優初值參數。

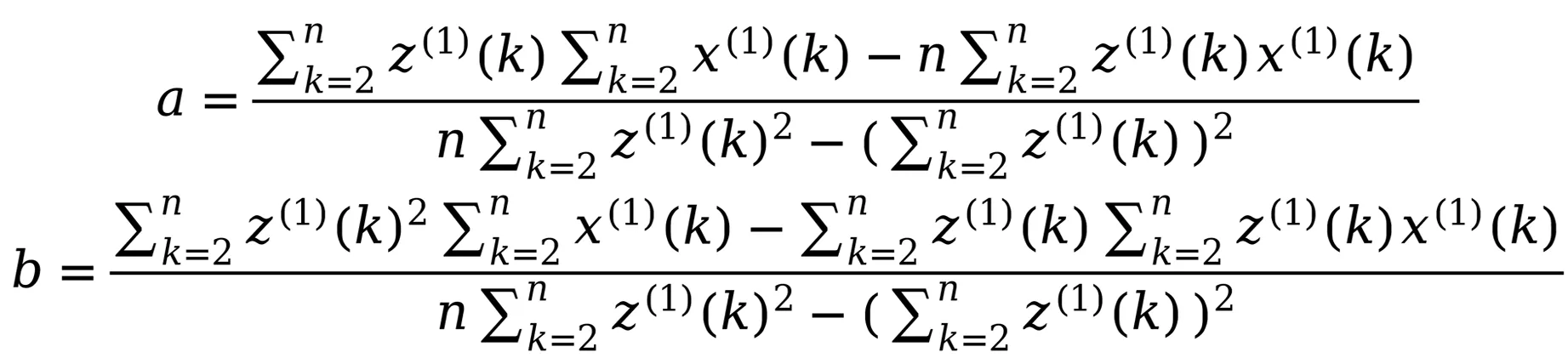
為了統一參數優化的目標函數與預測結果檢驗準則，本文選擇平均相對誤差最小化為目標，將初值、系統參數a和b、背景值等表達式作為約束條件，建立式(11)的非線性優化模型：

(11)

通過智能軟件matlab可以很方便地求解出初值參數φ以及參數a和b，將求得的初值x(1)(φ)代入式(10)中，便可求得權重系數λ的取值。所有參數均求解出來后，便可根據定義3.1.1進行模型的模擬和預測，最后實現基于全信息初值優化的GM(1,1)模型構建與應用。

4 實例分析

物流是指通過運輸工具實現物品在不同區域流動的過程，是將包裝、裝卸、搬運、儲存、流通加工、運輸、配送等基本功能有機結合以實現資源的合理配置及優化。隨著電子商務的發展，國內物流基礎設施布局也已完善，物流與電子商務密不可分，已經成為國民經濟發展中的關鍵環節之一，連接社會經濟的各個部分并使之成為一個有機整體，是國民經濟和社會發展的重要組成部分。我國物流行業經過多年的快速發展，目前已步入高質量發展的階段，擴張速度逐漸放緩。

2020年，全國社會物流總額約為300.1萬億元，但增速相較于2019年回落2.4個百分點，增速逐漸放緩。而從構成看，工業品物流占比接近90%，總額約269.9萬億元，按可比價格計算，同比增長2.8%。除工業品物流外，農產品物流、單位與居民物品物流、進口貨物物流以及再生資源物流約占10%。其中，農產品物流總額4.6萬億元、單位與居民物品物流總額9.8萬億元、進口貨物物流總額14.2萬億元、再生資源物流總額1.6萬億元。本文選取我國2011-2017年的數據進行建模，然后選擇移動平均法以及指數平滑法作為對照組來驗證本文所優化的模型的準確度，如圖2所示。

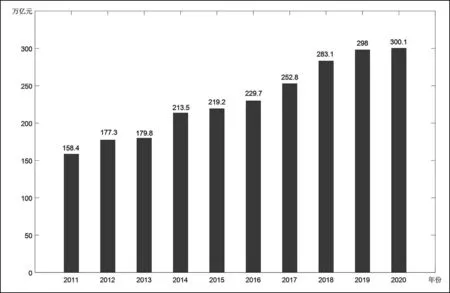
圖2 2011-2020年我國社會物流總額變化圖

具體建模過程如下：

原始數據為

X(0)={158.4,177.3,179.8,213.5,219.2,229.7,252.8}，

一階累減生成序列為

X(-1)={158.4,335.7,515.5,729,948.2,1177.9,1430.7}，

均值生成序列

Z(1)={247.05,425.6,622.25,838.6,1063.05,1304.3}

各模型結果如表1和圖3所示。

表1 三種模型的預測對比

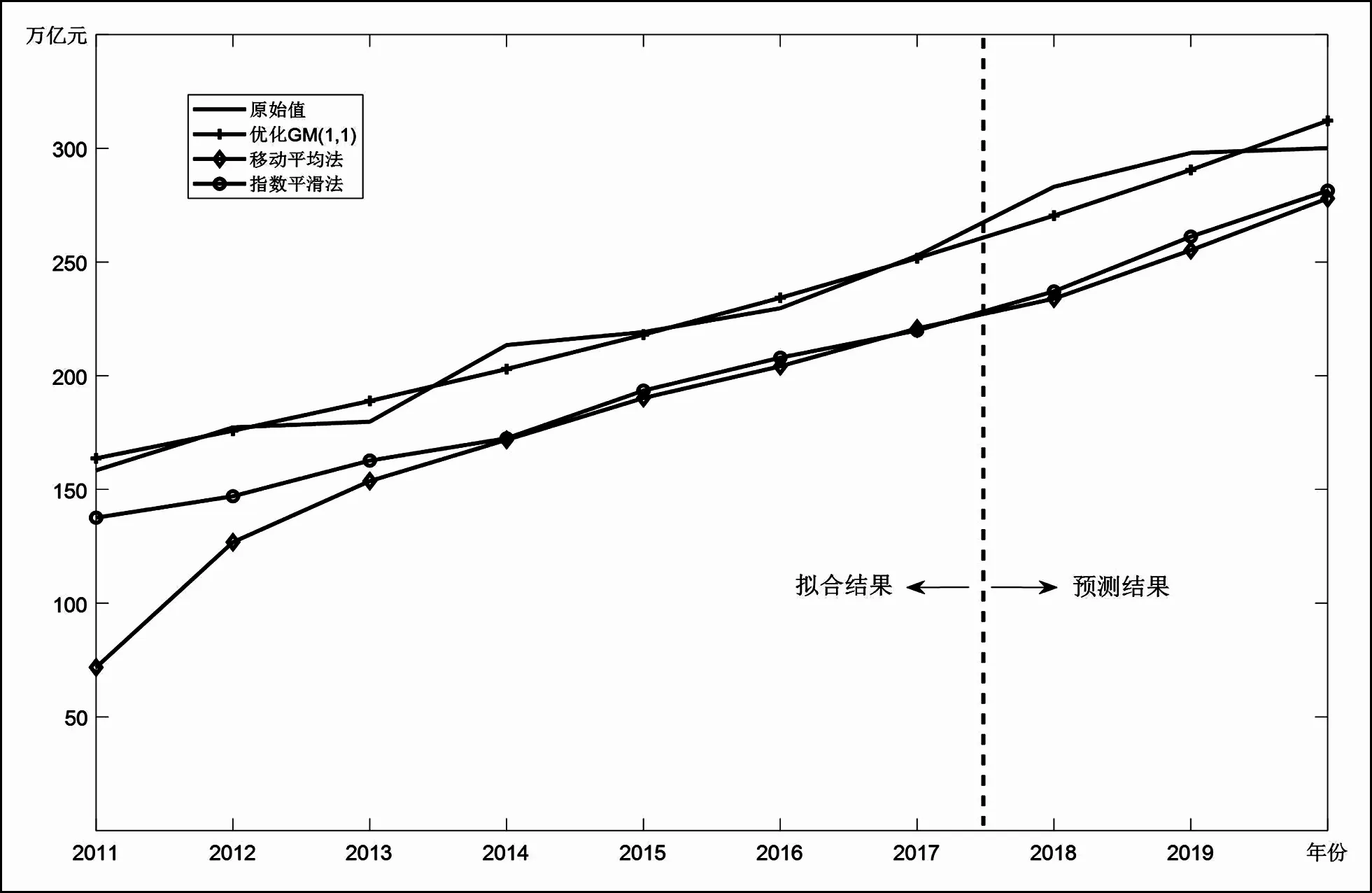
圖3 三種模型預測對比圖

可以看出，本文所構建的模型無論是擬合精度還是預測精度都遠高于對照組模型，模型的擬合精確度高達97.56%，預測精度高達96.33%，適合用于我國社會物流總額的預測。

5 結論

自灰色系統理論被提出以來，灰色預測模型作為灰色預測理論的核心和基礎之一，在廣大學者的不斷研究與探索中變得越來越完善，也在實踐檢驗的過程中逐漸得到了認可和廣泛應用。在現有研究中，關于GM(1,1)模型的建模優化的研究已有不少，對于GM(1,1)模型優化的研究大都聚焦于初值的選擇、背景值的構造、灰導數的構造、模型計算方法的改進等方向，但是對于全信息初值的構造卻不多見。

本文在前人研究基礎之上，基于初值方向，對GM(1,1)進行了優化。在初值的選擇上，構建了全信息初值，充分提取了系統的有效信息，從而有效地提高了模型的預測精度。此外，我們將就全信息初值優化的GM(1,1)模型成功地應用于我國社會物流總額的預測中，分析了我國社會物流總額由慢速增長到快速增長，然后再到慢速增長的發展趨勢，并對我國社會物流總額后續發展情況進行了預測，為相關部門制定發展規劃提供政策決策依據。

相較于傳統GM(1,1)模型以及前人基于單個方向對于GM(1,1)模型的優化，本文提出的全信息優化方法有效地提高了灰色GM(1,1)模型的精度，但是本文所構建的模型仍然只適用于短期預測，而不適用于中長期預測。此外，對于GM(1,1)模型的優化，除了全信息初值以外，還有其他優化方法以及組合方式，這些都是本文今后可以展開研究的方向。