基于偏最小二乘的多特性復雜過程監測方法

孔祥玉 陳雅琳 羅家宇 周紅平 葉興泰

(火箭軍工程大學 導彈工程學院，陜西 西安 710025)

現代工業生產過程是一個相對復雜的過程，且隨著現代工業設備發展趨于集成化、復雜化，大量的傳感器被布置到各個關鍵節點以采集大量的過程信息。如何從海量的數據中分析過程的變化并提取特征，成為新的研究熱點之一。相較于傳統的基于物理模型的方法，基于數據驅動的多元統計過程監測(MSPM)方法[1-3]不需要知道詳細的機理知識，已被廣泛應用于大型設備的健康狀態監測。多變量統計過程監測方法通過從過程數據中提取關鍵數據或關鍵信息來構建高效的過程監測模型。常用的方法包括主成分分析(PCA)、偏最小二乘(PLS)分析、獨立成分分析(ICA)[4-6]。

在上述方法中，基于偏最小二乘的分析方法被用于對關鍵性能指標的有效監測，通過構建因變量Y對自變量X的回歸模型，提取X的潛變量t和Y的潛變量u之間的協方差信息，同時解決了自變量之間的多重相關問題。為構造PLS合理的統計指標，Zhou等[7]提出了全潛結構投影(TPLS)算法，將X進一步分解到4個子空間，并在對應子空間分別構造統計量進行過程監測。然而，Qin等[8]考慮了TPLS分解的子空間過多、存在冗余的情況，提出了并行潛結構投影(CPLS)算法，有效地簡化了TPLS模型。由于基于傳統PLS斜交分解[9]得到的空間擴展方法，在質量相關子空間中存在對預測質量無用的信息，易引發誤報警。針對該問題，Yin等[10]提出了改進的潛結構投影(MPLS)算法，通過對X進行正交分解得到預測關鍵性能指標的質量相關子空間。

上述算法在過程監控中有較好的故障檢測效果，但在具有單一動態、非線性的系統或兩種特性同時存在的工業系統，利用上述算法進行故障檢測時，往往會導致監測結果不可靠，如出現誤報率過高等問題。針對上述問題，專家學者們提出了許多的解決思路。但在動態工業過程中，傳感器采集的過程數據往往受歷史時刻樣本的影響，不能有效地反映當前時刻的變化。近幾年，增廣數據矩陣因操作簡單受到了廣泛的關注。Ku等[11]基于增廣數據矩陣，將普通主成分分析擴展為動態主成分分析。但基于增廣數據矩陣的動態分析方法存在以下缺點：①模型僅關注方差信息，導致動態關系的可解釋性差；②隨著滯后次數的增加，加載矢量的維數和參數的數量急劇增加，增大了計算復雜度。為了提高模型對數據動態關系的描述，Li等[12]提出了一種利用動態潛在變量模型(DLV)的方法，通過建立向量自回歸(VAR)動態模型來表征潛在變量內部的自相關關系，使動態模型具有更加清晰的數學描述。受DLV思想的啟發，Li等[13]提出了結構化動態PCA算法，可以從原始的數據空間中提取DLV，在提高動態特征提取能力的同時，保持了動態模型的空間結構。之后，Dong等[14]提出了一種新的動態主成分分析算法(DiPCA)，該算法可以準確地提取一組動態潛在變量，以捕獲數據中動態變化最明顯的部分，保證了外部模型的輸出，也給出了動態潛在結構的顯式表達。

在復雜的工業系統中，除動態特性外，過程數據通常也呈非線性變化。為了將PLS應用到非線性過程，人們提出了一系列基于PLS的非線性算法。如Wold等[15]通過使用多項式進行非線性映射來改進PLS的內部模型；Rosipal等[16]提出了基于核函數的核偏最小二乘(KPLS)分析算法。由于基于核函數的方法避免了計算具體的非線性映射，易于理解，具有較強的泛化能力，能很好地解決其他方法的過擬合和欠擬合問題，因此在非線性過程中基于核函數的擴展算法成為了主流方法，如全核PLS(TKPLS)算法[17]、向核PLS(MKPLS)算法[18]、并發核潛結構(CKPLS)算法[19]、定向核PLS(DKPLS)算法[20]均在故障檢測方面取得了廣泛的應用。

上述方法雖然在動態過程和非線性過程的故障檢測中分別得到了大量的研究和發展，但不能有效應用于動態、非線性單獨存在的工業過程或兩種特性同時存在的多特性混合過程。針對該問題，本文提出了一種基于偏最小二乘的多特征提取算法(MFPLS)。該算法首先針對不同特性建立模型并提取特征，將原始的數據空間分解成4個子空間(動態子空間、線性子空間、非線性子空間以及殘差子空間)，然后針對不同空間構造統計量以實現復雜過程多特征的過程監測。最后以田納西-伊斯曼(TE)過程為實例，分析了本文所提出的算法的性能。

1 理論基礎

1.1 KPLS

線性PLS有效解決了自變量之間的多重相關問題，但利用線性模型來解決非線性問題時，會引入對回歸沒有幫助的噪聲，從而降低模型的泛化能力。針對該問題，核偏最小二乘被提出。設輸入數據、輸出數據分別為

X=[x0，x1，…，xm-1]T∈Rn×m

(1)

Y=[y0，y1，…，yp-1]T∈Rn×p

(2)

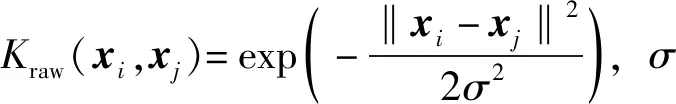
1.2 DiPLS

在動態過程中，當前時刻樣本受歷史樣本序列的影響呈動態變化。為了更加清晰地描述動態過程中PLS內外模型的關系，Dong等[23]提出了DiPLS算法，通過建立X的內在潛變量ti=Xwi與Y的內在潛變量ui=Yci之間的動態模型來表示動態關系(wi和ci為權重向量)，具體公式如下：

uk=β0tk+β1tk-1+…+βstk-s+rk

(3)

其中，tk、uk分別為當前時刻k的輸入、輸出得分，rk為殘差，s為動態系統的階次，βi為輸入得分的權重系數。則潛變量關系的預測模型可以表示為

(4)

其中，β=(β0,β1,…,βs)T，β?w為克羅內克積。

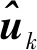
(5)

2 多特征提取方法的建模過程

針對動態、非線性特性單獨存在或兩種特性同時存在的混合系統的質量相關故障檢測問題，本文提出了基于偏最小二乘的多特征提取算法MFPLS。

為了提升模型的收斂速度和精度以及消除單位差異帶來的影響，需要先將獲取的原始輸入Xxun、輸出Yxun歸一化預處理為均值為0、方差為1的數據矩陣X、Y。隨后將數據矩陣X、Y分別擴充為以下矩陣：

Xi=[xi，xi+1，…，xi+N]T∈R(n-s+1)×m

(6)

Zs=[Xs，Xs-1，…，X0]∈R(n-s+1)×sm

(7)

Ys=[ys，ys+1，…，ys+N]T∈R(n-s+1)×p

(8)

式中：Xi為第i個數據矩陣(i=0,1,…,s)，即將數據矩陣X分成了s+1塊；Zs表示將每個數據塊Xi儲存起來，不改變樣本數只增加變量數，此時的Zs作為新的增廣輸入矩陣；Ys表示將數據的維度增大到和Zs一致，此時的Ys作為新的增廣輸出矩陣。

結合式(6)-(8)，動態內模型的目標函數(式(5))可以被重新描述為

(9)

其中，c、w為權重矩陣。然后使用拉格朗日乘子法優化該目標函數。DiPLS外部模型建模使用的迭代算法步驟如下：

(1)初始化β=(1,0,…,0)，us為Ys的任一列；

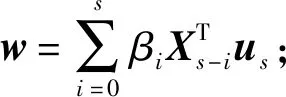
(3)計算X的得分向量ti=Xiw；

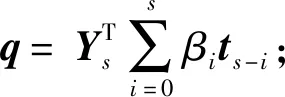
(5)計算Y的得分向量us=Ysq；

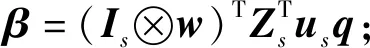
(7)返回步驟(2)，直到ti收斂。

由于輸入X的得分矩陣T=[t1t2…tA]無法直接從X計算得到，故引入權重矩陣R∈Rm×A(A為主元個數)：

R=W(PTW)-1

(10)

其中，W=(w1,w2,…,wA)，P=(p1,p2,…,pA)。

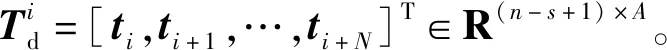
(11)

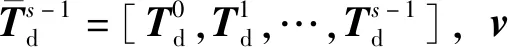
(12)

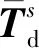
(13)

此時的輸入輸出預測殘差為

(14)

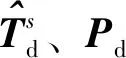
上述動態模型提取了動態分量，但在動態輸入殘差Ed中仍會存在線性變化的分量和自協方差信息，需要對Ed進行線性PLS的分解。此時，將DiPLS的殘差Ed∈R(n-s+1)×m、Yd∈R(n-s+1)×p作為線性部分的輸入和輸出矩陣。線性PLS的迭代步驟如下：

(1)取Yd的任一列并記為ud；

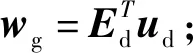
(3)計算Ed的得分向量tg并歸一化，即tg=Edwg；

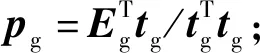
(6)計算Yd的得分向量ug并歸一化，即ug=Ydqg;

(7)返回步驟(2)，直到tg收斂。

由于輸入Ed的得分矩陣Tg=[tg1，tg2，…，tgA]無法直接從Ed計算得到，故引入權重矩陣Rg：

(15)

其中，Wg=(wg1,wg1,…,wgA)，Pg=(pg1,pg1,…,pgA)。此時，Ed、Yd被分解為

(16)

其中，Tg、Pg分別為輸入Ed的得分矩陣和負載矩陣，Qg為輸出Yg的負載矩陣，Eg、Yg分別為Ed、Yd的線性殘差。

農產品的類別特別多，然而當前國內對于農產品缺乏詳細地標準，無論哪一種食品均存在好壞的差別，然而在農產品市場上并未結合具體情況制定相關的標準，這便較易導致交易雙方在認知上存在一定地偏差。很多農產品在流入市場以前，在品質與售價方面均是不規范的，顧客在選購產品時，也無法分辨產品的好壞，為此，會偏向于選購部分有明確標準的進口農產品，這對于國內農業的發展是非常不利的。

上述線性模型提取了線性分量，但在線性殘差Eg中仍然存在非線性信息。因此，需要對Eg進行非線性PLS分解。殘差Eg的非線性映射為

Eg∈R(n-s+1)×m→Φ(Eg)∈Γ(n-s+1)×(n-s+1)

(17)

將經過非線性映射函數得到的高維數據記為K，為了消除高維特征空間Γ中的均值效應，需要對數據進行中心化預處理，即

(18)

其中，K1為中心化預處理后得到的數據，nr為輸入Eg的列數，K=Kraw為殘差Eg通過核函數得到的直接映射矩陣，Ir為n-s+1維的單位矩陣。KPLS非線性回歸建模的步驟如下：

(1)輸入Eg，隨機初始化輸出ur；

(2)對數據進行非線性映射并中心化處理為K1；

(3)計算得分向量tr并歸一化，即tr=K1ur；

(5)計算Yg的得分向量并進行歸一化處理，即ur=Ygqr；

(6)返回步驟(2)，直到ur收斂；

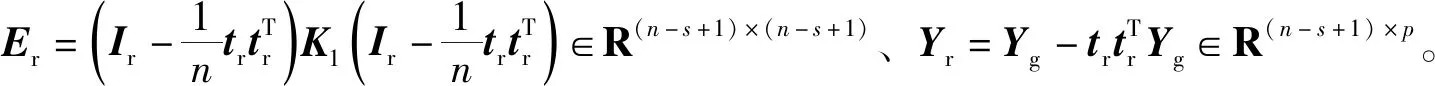
此時，得到的KPLS模型為

(19)

本文提出的MFPLS算法需要先對原始的數據集進行標準化處理，然后按如下步驟分別提取不同的特征：①對標準化后的數據進行動態內PLS處理；②將DiPLS處理后的動態殘差進行線性PLS處理；③將PLS處理后的線性殘差進行KPLS處理。該算法既充分考慮了多特性混合系統的動態、非線性和線性性能，也考慮了上述特性單獨存在的系統，并在動態殘差空間進行多次分解，得到僅含噪聲的殘差子空間。MFPLS算法的原理圖如圖1所示。

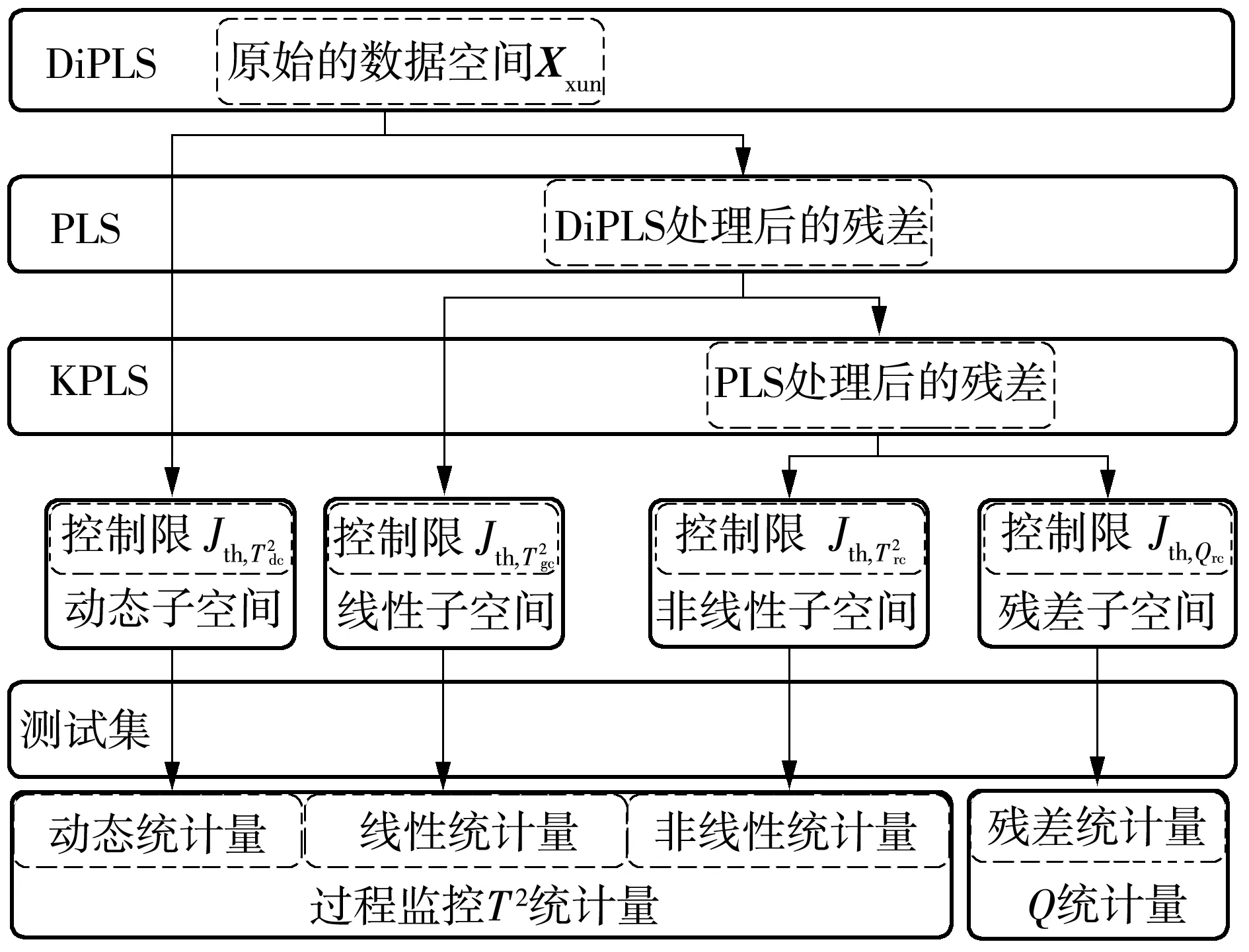
圖1 MFPLS算法的原理圖Fig.1 Schematic diagram of MFPLS algorithm

這樣可以得到原始數據Xxun被完全分解的情況,即

(20)

也就是原始的數據空間被分解成4個子空間，它們分別是動態子空間SD、線性子空間SG、非線性子空間SR和殘差子空間SS。PLS分解的子空間是斜交的，其中動態、線性和非線性子空間是質量相關的子空間，殘差子空間是質量無關的子空間。

3 MFPLS的過程監測策略

3.1 MFPLS的過程監控指標

故障檢測中常用平方預測誤差(SPE)統計量(又稱Q統計量)來監測殘差空間，用HotellingT2統計量來監測質量相關子空間，即用SPE統計量來監測質量無關的故障，用T2統計量來監測質量相關的故障，具體的公式為T2=tTΛ-1t和Q=eTe。對于核PLS算法，Q統計量的計算公式如下：

(21)

(22)

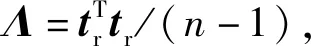
統計量的控制限為

(23)

(24)

3.2 MFPLS的過程監測流程

當給出新的測試集輸入Xce和輸出Yce時，標準化處理和數據擴充即能得到輸入Xnew和輸出Ynew。

最后計算總的殘差統計量：

(25)

(26)

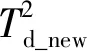
MFPLS算法進行故障檢測的主要步驟如下：①對直接獲取的訓練集Xxun和Yxun按照適合的方式進行預處理，并建立數學模型，計算各自的控制限；②利用訓練后的模型計算測試數據的統計量；③比較新統計量與訓練集的控制限，以判斷故障是否發生。

4 田納西-伊斯曼實驗驗證

20世紀90年代，美國Eastman公司開發的化工模型仿真平臺TE過程是一個典型的非線性、開環不穩定的復雜過程，包含快速和緩慢的動態混合特性，主要由反應器、冷凝器、氣液分離器、循環壓縮器和汽提器5部分動態模型組成，被廣泛應用于多特性復雜過程的故障檢測與故障診斷驗證[25-26]。為了保護該過程的知識產權，Downs等[27]沒有發布有關該過程的詳細組件，并對該過程中的工藝和操作條件等進行了修改。

TE過程中的訓練集樣本是在25 h仿真運行下獲取的，觀測數據總數為500；測試集樣本是在48 h仿真運行下獲取的，觀測數據總數為960。不同的訓練集、測試集樣本分別代表不同的故障類型。TE過程主要包括41個測試變量XMEAS(1-41)和12個控制變量XMV(1-12)，正常數據集作為訓練樣本，160個正常樣本和800個故障樣本組成的數據集作為測試樣本。故障又分為質量無關與質量相關的故障。關于TE過程的變量含義、故障類型的詳細描述可參看文獻[27-29]。

MFPLS中主元個數由交叉驗證或平均特征值法確定，針對不同的質量相關故障，主元個數有所不同，3個子空間的主元數分別為Ad=7，Ag=6，Ar=5。采用粒子群優化算法確定窗長q為3，核函數比例系數σ為300。

本文選取的輸入變量X為22個過程變量XMEAS(1-22)和11個控制變量XMV(1-11)；質量輸出變量為過程變量XMEAS(35)。選取的對比對象是動態總PLS(DTPLS)[12]和TKPLS。DTPLS算法將數據X的空間分解為質量相關的動態空間SD、質量無關的動態空間SWD、質量無關的靜態空間SWG和殘差空間SDT。TKPLS算法將數據X的空間分解為負責預測輸出Y的非線性空間SR、與輸出Y正交的非線性空間SZ、殘差中包含較大差異的線性空間SG和僅含噪聲的線性殘差空間STK。主元個數通過交叉驗證分別得到ADT=4，ATK=8。

4.1 故障檢測時刻的實驗

TE過程用于建模的訓練集Xxun包含500個正常的樣本，用于在線檢測的測試集Xce包含160個正常樣本和800個故障樣本，即測試集Xce中從第161個樣本開始就是故障樣本。一般來說，某種算法先檢測到故障，就表明該算法有較快的故障檢測速度。故在本實驗中，采用故障檢測時刻來展示不同算法進行故障檢測的優劣性，具體的結果如表1所示，表中*表示3種算法在TE過程中能快速檢測到故障的最優時刻，^表示DTPLS和MFPLS對動態特性的檢測效果的最優值，#表示TKPLS和MFPLS對非線性特性的檢測效果的最優值。

表1 3種算法的故障檢測時刻對比Table 1 Comparison of fault detection time of three algorithms

由于MFPLS算法采用粒子群優化算法確定的窗長q為3，結合動態PLS的矩陣擴充方式，此時故障發生的樣本數變為161-q+1=159。故對于MFPLS和DTPLS算法，測試集Xce中從第159個樣本開始為故障樣本；對于TKPLS算法，測試集Xce中從第161個樣本開始為故障樣本。經過統計得知，對于故障IDV(1-15)，DTPLS的質量空間能快速監測到故障數為18，TKPLS能快速監測到故障數為10，MFPLS能快速監測到故障數為19。相較于TKPLS算法，使用動態類PLS算法能快速地捕獲到故障的發生，且MFPLS算法捕捉故障發生的能力優于DTPLS算法。將MFPLS的動態子空間與DTPLS的質量相關的動態子空間的故障檢測時刻進行對比，可以知道DTPLS算法能較好地監測到故障的發生。將MFPLS的非線性子空間與TKPLS的負責預測輸出的非線性子空間的故障檢測時刻進行對比，可以明顯看出，TKPLS能較快檢測到故障IDV(4-7,9,12-14)的發生，而除了呈階躍變化的微小故障IDV(3)外，MFPLS可以快速地監測到非線性子空間發生的所有異常。故障2是呈階躍變化的濃度故障，TKPLS、DTPLS、MFPLS算法對故障2的監測效果和故障發生時刻的放大圖展示如圖2所示。由圖中可知：MFPLS的動態子空間在第173個樣本檢測到故障的發生，DTPLS則在第180個樣本檢測到故障的發生；MFPLS的非線性子空間在第160個樣本檢測到故障的發生，DTPLS則在第191個樣本檢測到故障的發生。

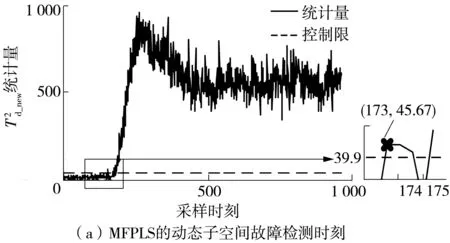
圖2 3種算法的故障檢測時刻結果Fig.2 Fault detection time results of three algorithms

綜上所述，DTPLS算法對動態特性有較好的故障檢測效果，MFPLS算法對動態子空間也有良好的故障檢測效果。特別是，將數據空間經過DiPLS算法去除動態特性后，MFPLS算法能在線性和非線性子空間較迅速地監測到故障的發生，說明了本文所提算法MFPLS對動態、線性和非線性混合的系統能快速地捕獲到故障的發生，有較好的故障檢測效果。

4.2 質量相關故障檢測率的實驗

本文采用有效檢測率(FDR，RFD)和故障誤報警率(FAR，RFA)[9,30-31]進行故障檢測效果的驗證。設Near為有效報警數，Nfpr為誤報警數，Nfsn為故障樣本數目，則

(27)

(28)

其中，FDR用于反映質量相關故障的檢測情況，FAR用于反映質量無關故障導致的誤報警情況。

DTPLS、TKPLS和MFPLS對質量相關故障的檢測結果如表2所示。由表中可以發現：在監測故障IDV(1,2,6-8,12,13)時，MFPLS算法的有效報警率有較大的提高；對于非線性特征，MFPLS在進行IDV(1,2,6,7,14)故障檢測時的故障檢測率達到99%及以上，對IDV(8,12,13)的故障檢測率達到95%及以上，TKPLS對IDV(10)的故障檢測率優于MFPLS；對于動態特征，MFPLS在進行IDV(1,6,14)故障檢測時的故障檢測率達到98%及以上，對IDV(2,13)的故障檢測率達到90%及以上，DTPLS對微小故障IDV(5)的檢測率優于MFPLS；相較于DTPLS的動態監測效果，MFPLS的動態監測效果均有明顯的提高。

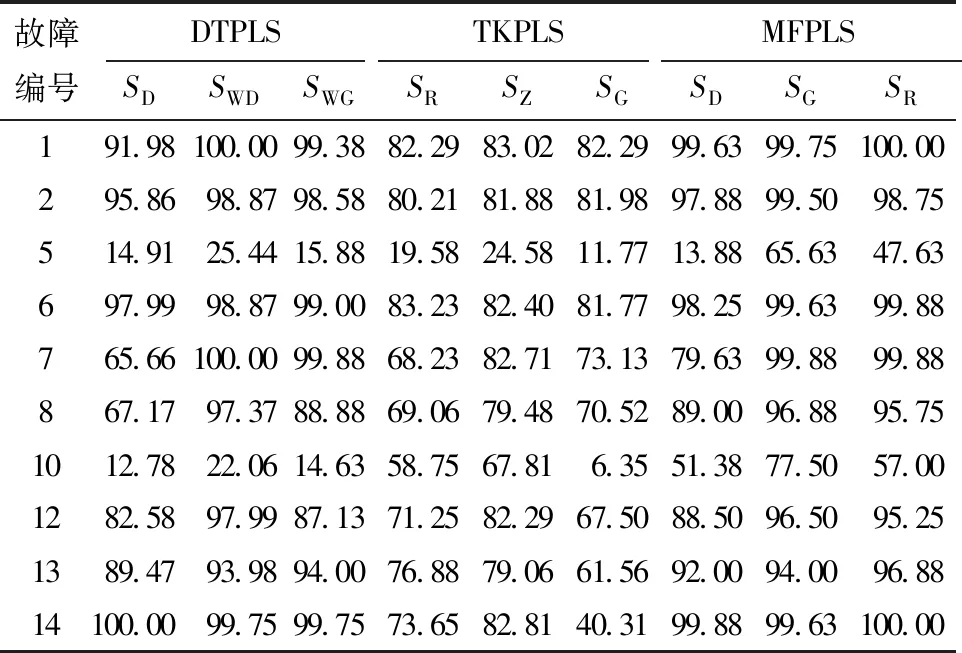
表2 3種算法的質量相關故障報警率Table 2 Quality related fault alarm rates of three algorithms

故障8是隨機變化的供料濃度故障，TKPLS、DTPLS、MFPLS算法對故障8的監測效果和局部放大圖如圖3所示。由圖中可以發現：對于動態特性，相較于DTPLS，MFPLS的統計量能監測到較多的故障信號，故障檢測率提高了將近20%，而DTPLS對故障樣本會有較多的誤報警情況；對于非線性特征，相較于TKPLS，MFPLS可以監測幾乎所有的故障信號，故障檢測率有了較大的提高，但MFPLS算法對正常數據會有更多的誤報警情況；與DTPLS的動態特性、TKPLS的非線性特性相比，MFPLS對質量相關故障的動態特性、非線性特性的監測效果均有將近20%的增長，但MFPLS算法對非線性空間的監測效果不理想。綜上所述，MFPLS算法提高了質量相關故障的檢測率，且均能對這幾類質量相關故障進行有效監控。

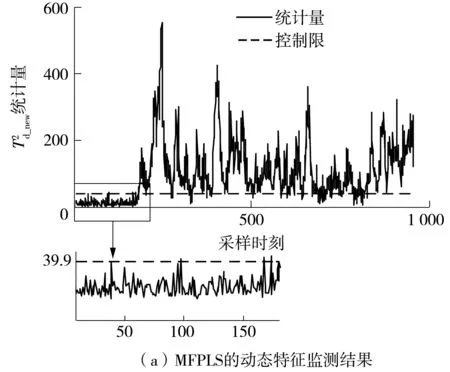
圖3 3種算法的質量相關故障檢測結果Fig.3 Quality related fault detection results of three algorithms

4.3 質量無關故障檢測率的實驗

DTPLS、TKPLS和MFPLS對質量無關故障的檢測結果如表3所示。從表中可以發現：當DTPLS在監測質量無關故障時，IDV(3,9,15)的有效檢測率低于8%，而IDV(11)的有效檢測率將近70%，IDV(4)的有效檢測率高達100%，即DTPLS對IDV(4,11)的監測有較高的誤報警率；TKPLS在進行過程監測時，IDV(3,9)的有效檢測率低于8%，而殘差中包含較大差異子空間的有效檢測率低于5%，基本維持在1%附近，這種現象說明TKPLS能對數據進行有效的分解，誤報警的情況得到了明顯的改善；MFPLS在監測動態質量無關故障IDV(3,4,9,15)時，有效檢測率基本維持在3%附近，發生誤報警的情況明顯減少，對故障IDV(3,4,15)的誤報警率甚至低于4%，但在監測線性子空間和非線性子空間時，誤報警率大多都高于50%。

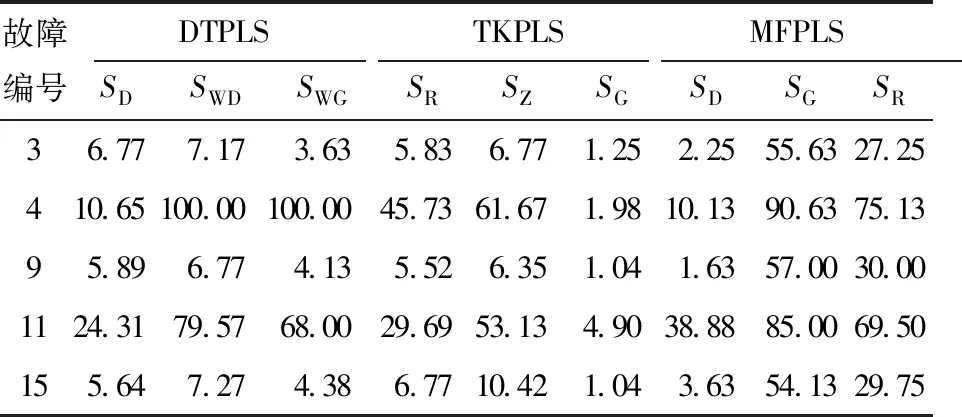
表3 3種算法的質量無關故障報警率Table 3 Quality independent fault alarm rates of three algorithms

故障3是階躍變化的供料溫度故障，TKPLS、DTPLS、MFPLS算法對故障3的監測效果如圖4所示。對比圖4可以發現，MFPLS對動態特征的故障檢測效果較好，對非線性特征的誤報警率比TKPLS大一些。這是因為該算法為了提高非線性部分的檢測效果而剔除了原始數據中的動態和非線性信息。但該算法對質量無關部分的故障具有良好的檢測效果和較低的誤報警率，且對動態特征的誤報警率不受影響。與TKPLS、DTPLS方法相比，MFPLS具有更低的計算成本，且能用一種更容易解釋的方式來獲取過程數據中的動態、線性和非線性特征。

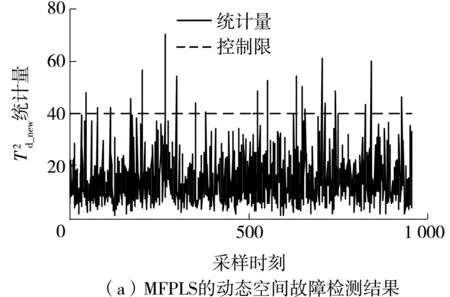
圖4 3種算法的質量無關故障檢測結果Fig.4 Quality independent fault detection results of three algorithms

綜上所述，本文提出的MFPLS算法解決了線性PLS、非線性PLS、動態內PLS對混合特性有較低的故障檢測率問題，擴大了PLS的應用范圍；同時考慮了過程數據中的動態、線性和非線性特征，并將不同的特征變化分別反映在動態、線性和非線性子空間中，故同樣適用于對動態、非線性特性單一存在的過程或兩種特性同時存在的工業過程進行監測。此外，本文算法有效降低了質量無關故障的誤報警率，在多特性復雜過程中具有更加良好的故障檢測性能。

5 結論

針對動態、非線性或動態和非線性特征同時存在的系統的質量相關故障檢測問題，本文提出了一種基于PLS的在線監控多特征提取算法MFPLS。該算法將動態內PLS、線性PLS、核PLS模型有效地結合在一起，提取出的豐富信息提高了模型的可解釋性，也提高了過程監控性能。與DKPLS和TKPLS相比，MFPLS提高了原始數據的利用效率，克服了動態干擾，提高了質量相關故障的檢測率，同時擴大了PLS算法的應用范圍。本文所提算法在質量無關故障的非線性特征檢測方面的效果不夠理想，這是由于數據經過多次特征提取造成的，如何降低多次特征提取時質量無關故障的漏報率，是今后亟需解決的問題。在基于多特征提取算法的基礎上，如何進行故障診斷也是今后的研究方向。