基于局部軟約束優化的無人機航跡規劃方法
陳朋 江勇奇 俞天緯 黨源杰 宦若虹
(1.浙江工業大學 計算機科學與技術學院,浙江 杭州 310023;2.浙江工業大學 信息工程學院,浙江 杭州 310023)
近年來,隨著無人機(UAV)廣泛地應用于空中拍攝、災后救援和城市安防等各種場景,人們對無人機自主導航能力的要求也逐漸提高,尤其是在長距離導航方面。航跡規劃是實現無人機自主導航的關鍵技術之一,其可分為前端路徑搜索和后端軌跡優化[1]。前端通過路徑搜索算法獲得空間上無碰撞的初始路徑,但缺少在時域上對無人機速度和加速度的設定;后端則在前端基礎上進行優化,生成更加平滑、安全且適合無人機動態飛行的軌跡。
前端路徑搜索主要分為基于采樣的和基于圖搜索的兩類方法。基于采樣的代表算法快速探索隨機樹(RRT)[2]從配置空間中隨機地抽取樣本,并引導樹向目標生長。雖然RRT算法能夠有效地找到可行的路徑,然而沒有漸近最優性。Karaman等[3]提出了基于采樣的漸進最優方法RRT*,隨著樣本數的增加,該算法最終會收斂到全局最優解。基于采樣的方法雖能有效地解決了復雜約束的路徑規劃問題,但算法效率不穩定。基于圖搜索的方法雖未必能找到最優路徑,但效率極高且穩定,更符合無人機的實時要求。基于圖搜索的代表算法A*將配置空間離散化,把路徑搜索問題轉化為圖搜索問題,根據圖中節點代價尋找最優路徑[4]。近年來人們通過改進算法A*來解決相應的實際問題。Dolgov等[5]提出了基于物體實際運動約束的混合A*算法,生成符合車輛運動規律的軌跡。張慶等[6]通過融合跳點搜索(JPS)策略來改進A*算法,大大減少了拓展的節點和尋路算法的內存消耗。但上述對A*算法的改進較為復雜,目前還只應用于二維地圖。而Theta*算法[7]利用視線檢查改進A*算法并且適用于三維環境。該算法在遍歷節點時檢測當前節點和上個節點的父節點之間的線空間中是否存在視線,若存在,則刪除中間節點以獲得比A*算法更短的路徑。但Theta*算法僅通過簡單的避障檢測并沒有解決A*算法遺留的安全問題,且節點代價計算方式尚未考慮到無人機轉彎情況。
后端軌跡優化一般先把軌跡表示成以時間為變量的分段多項式形式[8],然后通過設計目標函數和添加相應的約束條件進行優化。目前許多軌跡優化方法被提出來,并逐漸形成兩種流派:硬約束法[9-12]和軟約束法[13-14]。硬約束法主要是將軌跡表達式設為目標函數,并通過構建飛行走廊來添加硬性的約束條件,即目標函數中的解必須要滿足這些條件。根據飛行走廊的形狀,硬約束法可分為長方體法[9-10]、球體法[11]和多面體法[12]。以長方體法為例,首先將前端算法獲得的每個航路點構造為小立方體,然后延伸這些立方體的面,直到它們接近障礙物,形成一條走廊,再設計最小變加速度目標函數,結合走廊約束條件,形成凸二次規劃問題進行求解。軟約束法則直接將約束條件設計成目標函數,因此這些約束條件只需要傾向于滿足即可,但為了生成可靠的軌跡,需利用環境信息構建歐氏符號距離場(ESDF)以提取梯度信息來加強約束。Zhou等[13]利用B樣條的凸包性質,將梯度信息和動力學約束結合為目標函數,提高了軌跡的平滑度和安全性。Lin等[14]和筆者前期工作[1]中利用環境梯度信息最小化碰撞代價、平滑度和動力學可行性的損失函數,以獲得最佳軌跡。硬約束法雖然可以利用飛行走廊避免碰撞,但依舊容易生成靠近障礙物的軌跡,而軟約束法在一定導航距離內可100%生成安全性更高的軌跡。但若目標點距起點較遠,環境更復雜,建立ESDF所要處理的信息量更大,軟約束法效率和成功率也會明顯下降[15]。另外,近年來不少優化無人機飛行速度的時間分配方案被提出。Gao等[16]提出了一種基于離散變量的時間分配方法,將優化問題轉化為凸二次錐規劃(SOCP)并求解。Zhang等[17]首次針對非凸輸入約束提出了基于四旋翼微分平坦度特性的時間最優規劃方法。
為了提高無人機在長距離導航中的規劃效率和飛行效率,本文提出了基于局部軟約束優化的無人機航跡規劃方法。首先基于改進的Theta*算法獲取初始軌跡,并針對原算法的安全問題加入了安全距離約束,同時增加對擴展節點轉彎代價的計算;然后提出了高效局部優化策略以限制ESDF構建范圍和時間,采用軟約束法對初始軌跡中低質量片段進行優化,而對高質量片段僅做簡單的平滑處理,同時分別針對軌跡中的直線段和曲線段設計了低階和高階的時間分配來提升無人機的飛行速度;最后通過仿真和實際飛行來測試本文方法的性能。
1 基于改進Theta*的路徑搜索算法
本文提出的無人機航跡規劃方法框架見圖1,包括前端路徑搜索和后端軌跡優化。改進Theta*算法的流程圖如圖2所示,相比于前期工作[1],Theta*算法利用視線檢查機制能刪減更多的冗余節點,如圖3(b)和3(c)所示,因而本文算法沿用了該機制。另外,受文獻[18]的啟發,本文將視線檢查提前而非放在最后進行,這樣只需檢查上一個節點的最優鄰節點而不必檢查每個鄰節點,從而減少多余的檢查工作。同時,為了獲取高質量的初始軌跡,加入了安全距離約束和轉彎代價函數。
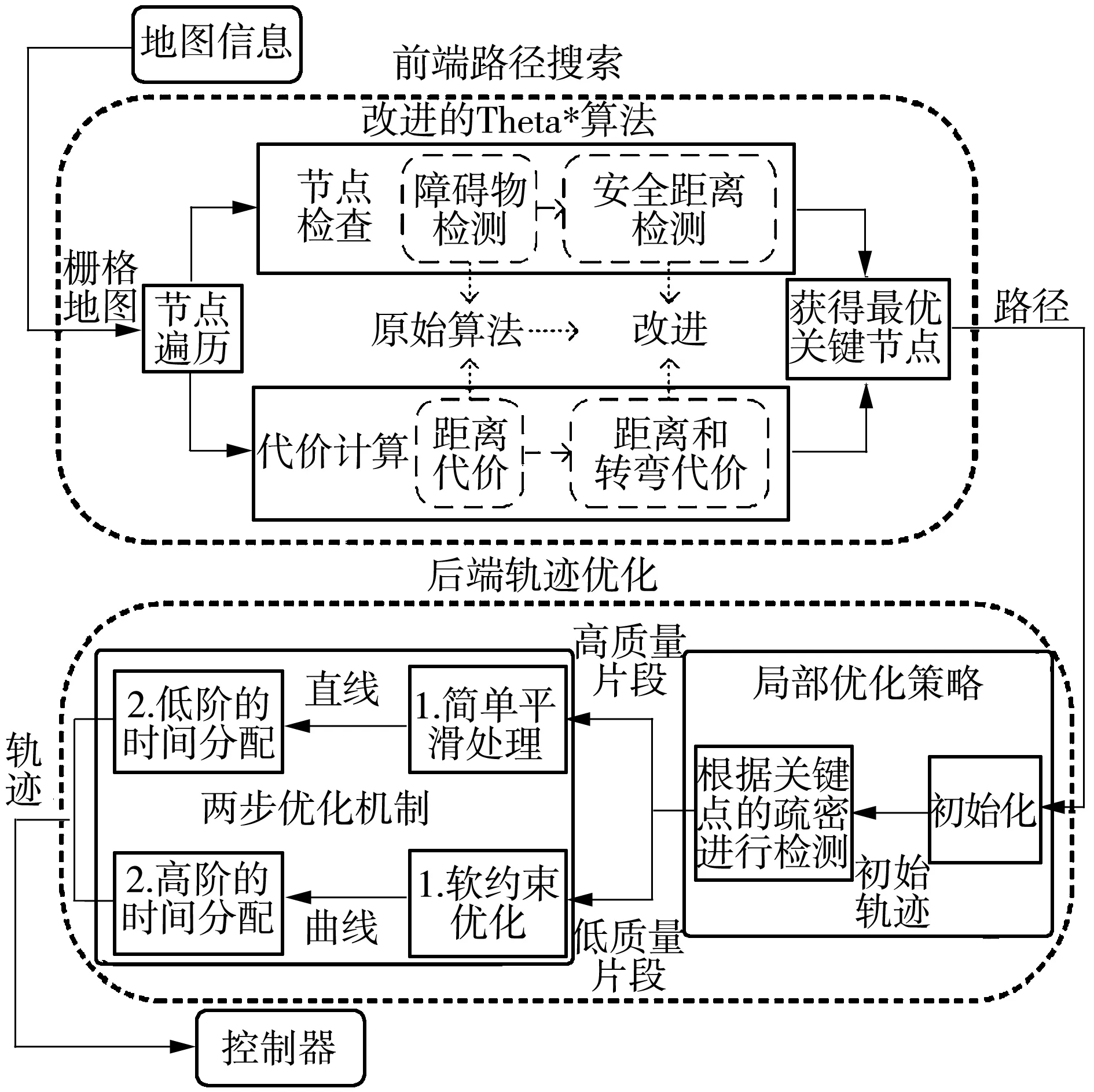
圖1 本文航跡規劃方法的框架Fig.1 Framework of the proposed trajectory planning method
1.1 安全距離約束
如圖3(c)所示,關鍵節點仍然靠近障礙物,但實際中無人機并不是節點,存在一定體積,很可能會與障礙物相撞。為了解決這個問題,在視線檢查和安全檢查中的節點檢查部分用安全距離檢測代替障礙物檢測,如圖2所示。具體檢測步驟如下:首先提取離被檢測節點在dc以內的節點,dc即為安全距離;然后檢查這些節點是否為障礙物,其中屬于集合P和C中的節點不需要再次檢查,因為這些節點已經在之前的循環中檢查過了。在安全檢查中,通過安全距離檢測來檢查當前節點及其相鄰節點是否與障礙物保持安全距離,以確保由Theta*算法獲得的關鍵節點的安全;在視線檢查中,通過安全距離檢測檢查連接相鄰關鍵節點的線路上的節點是否安全,以確保連接線路也安全。圖3(d)中的虛線區即為安全距離約束下獲得的安全區域,整個路徑都能與障礙物保持一定的距離,使無人機有足夠的飛行空間。但是安全距離r的值要相對較小,若超過一定閾值,會使算法的搜索效率大大下降,所以需要根據實際飛行要求設定r為相對較小且能保證安全的值。
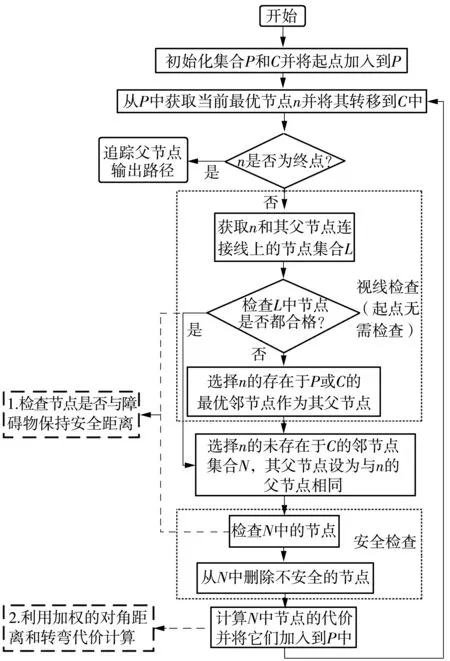
圖2 改進Theta*算法的流程圖Fig.2 Flow chart of the improved Theta* algorithm
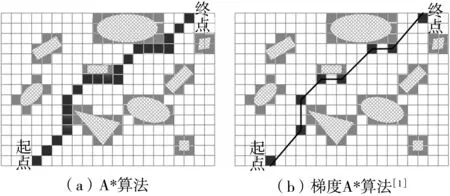
圖3 不同算法的路徑Fig.3 Paths of different algorithms
1.2 代價函數的改進
Theta*算法遵循A*算法的總代價函數f(ni),為
f(ni)=g(ni)+h(ni)
(1)
式中,g(ni)為節點ni和起點之間的代價函數,h(ni)為ni和終點ngoal之間的代價函數(即啟發式函數)。文中g(ni)和h(ni)的代價計算是相同的:
g(ni)=g(ni-1)+H(ni-1,ni)
(2)
h(ni)=H(ni,ngoal)
(3)
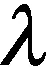
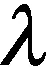
(4)
為了便于算法的實現,將環境視為三維網格地圖[19]。因此,采用對角距離來計算成本,比曼哈頓距離更精確,而且避免了歐氏距離中的平方根運算。設dx、dy、dz是節點ni和nj的三維坐標之差,dmin、dmed、dmax是它們的最小值、中值和最大值,則hd(ni,nj)定義為
|dmax-dmed|
(5)
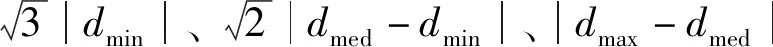
此外,考慮飛行中轉彎帶來的能量消耗和時間消耗,本文設計了轉彎代價函數ht(ni,nj)。計算出節點ni和其父節點ni.p構成的向量vni.p→ni與節點ni和nj構成的向量vni→nj之間的夾角,即得到無人機在當前節點ni的真實轉彎角度,并表示為弧度作為轉彎代價的值,即
(6)
2 高效的軌跡優化方法
2.1 局部優化策略
前端算法中有安全距離的約束,使初始路徑存在一定的安全保障,故不需要對整個路徑進行優化,即可以采取局部優化策略來減少優化工作和提升方法效率。
首先,本文用s段貝塞爾曲線來表示軌跡:
(7)
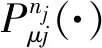
(8)
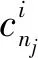
初始路徑由若干個關鍵點(起點、終點和拐點)組成,因此先采用1階貝塞爾曲線(即直線)連接相鄰關鍵點形成初始軌跡。但這樣的軌跡存在如下問題:①拐點處不平滑;②在拐點密集處(如圖4中虛線圓內),障礙物也密集,無人機發生碰撞的概率較大,存在安全隱患;③采用低階貝塞爾曲線對拐點密集處同時進行時間分配和平滑處理是困難的。因此,本文考慮對超過一個拐點的局部進行進一步優化,并用高階貝塞爾曲線表示,而其他部分(如局部單個拐點)只用低階貝塞爾曲線進行簡單的平滑處理,未優化的直線部分則保留。整個局部優化策略算法描述如下:
{輸入:初始軌跡。
輸出:最終軌跡。
初始化:從初始軌跡中提取包括關鍵點在內的等間距航點(如圖4所示,航點個數根據軌跡長度和航點間距大小而定),并從起點到終點依次存入W數組。W數組中關鍵點的索引按順序存儲在K數組中。這樣關鍵點的間距
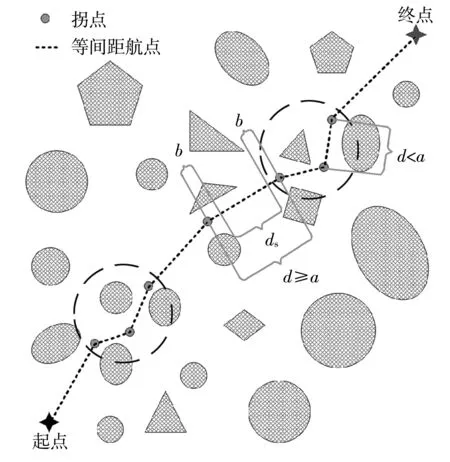
圖4 局部優化策略Fig.4 Local optimization strategy
d可以通過索引相減獲得的航點個數來表示,相比歐氏距離的計算,此方法減少了計算量,同時調參更方便。
局部優化檢測(省略對起點和終點的處理)
fori=1 ton-1 do ∥n為關鍵點個數且大于3
forj=i+1 ton-1 do
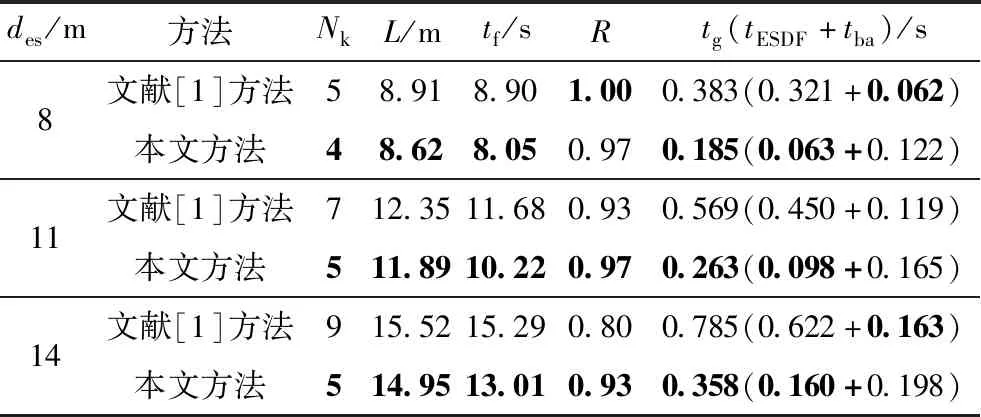
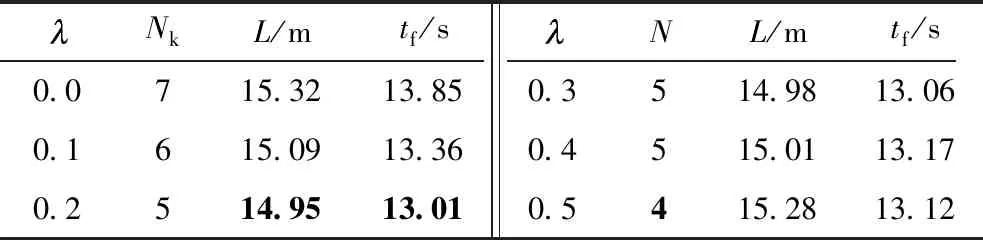
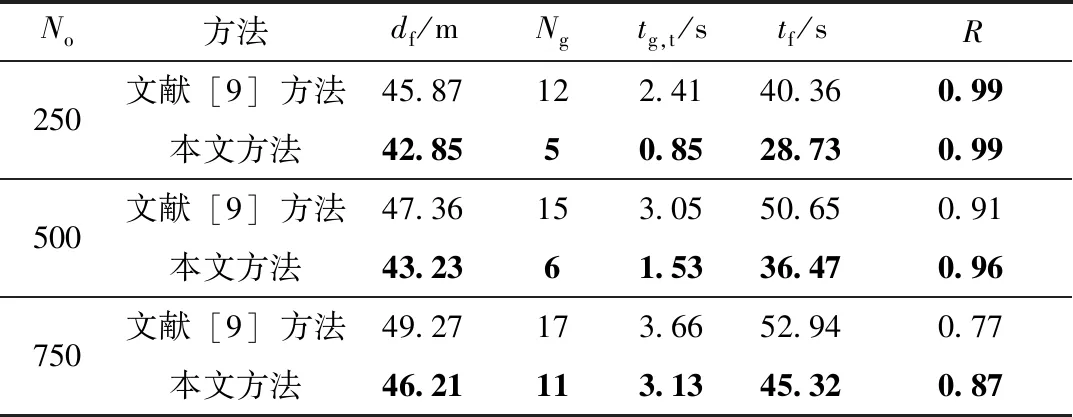
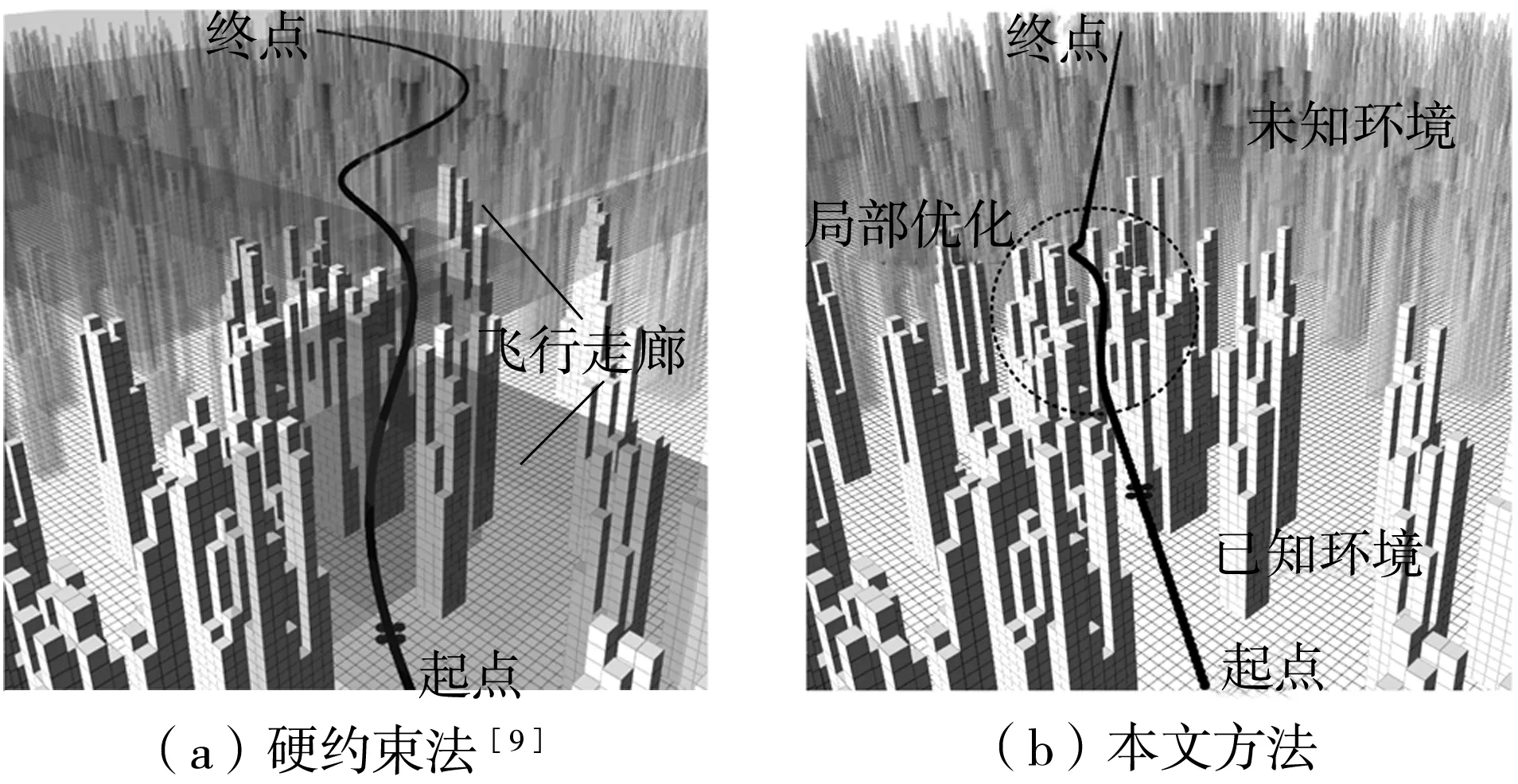
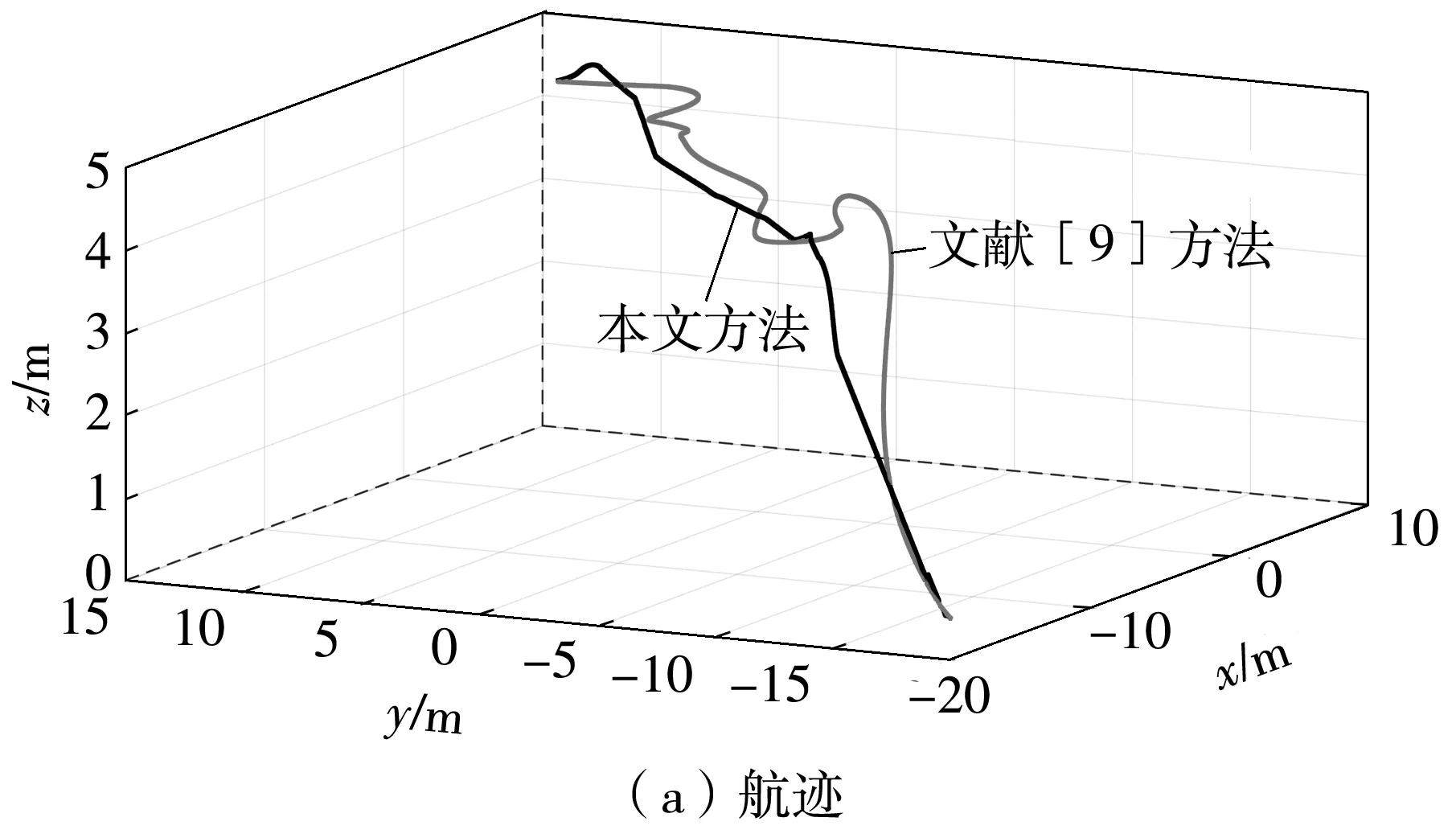
if (K[j]-K[j-1]) else break; end for if(j==i+1) 此時拐點W[K[i]]與下一個拐點W[K[i+1]]的間距大于a個航點間距,W[K[i]-b]、W[K[i]]、W[K[i]+b]被作為2階貝塞爾曲線的控制點,對相應的軌跡片段進行平滑處理; else 此時拐點W[K[i]],W[K[i+1]],…,W[K[j]]的間距d都小于a個航點間距,這些拐點與W[K[i]-b]、W[K[j]+b]被作為局部軟約束優化的關鍵點,對相應的軌跡片段進行優化; /*提取W[K[i]-b]和W[K[j]+b]兩個航點是為了保證未優化的直線段和優化后的曲線段連接處的平滑性,具體優化方法詳見2.2節*/ i=j;∥從j開始繼續循環 end for} a值決定了局部優化范圍,b值決定了平滑范圍。平滑一般只處理直線、曲線的連接處,范圍較小,實驗中b的范圍為[2,4]。a越大,軌跡中局部優化范圍越大,直線段數量越少,算法效率越低,因此a不宜過大;a越小,軌跡優化效果越不明顯,會影響安全性。另外,為了讓無人機在直線段有足夠的距離加減速,以保證直線、曲線之間的速度連續性,直線段長度ds(如圖4所示)需滿足 (9) 式中:dl為航點間距,實驗中設為0.1 m;vmax、amax分別為無人機最大的速度和加速度。因此a也與無人機設定有關,實驗中a的范圍為[10,30]。 在優化前需先構建歐氏符號距離場(ESDF),它能為其所在范圍內每一個體素提供該體素與最近障礙物的歐氏距離,一般采用截斷距離法[20]構建。因為局部優化只需要局部的障礙物信息,所以只需構建局部ESDF而非全局,這樣也能減少相應的規劃時間。首先采用局部優化策略得到某個軌跡段的所有關鍵點坐標(xi,yi,zi)|i=1,2,…,n,分別比較它們的x、y、z坐標值,得到x、y、z坐標的最小值和最大值(xmin、xmax、ymin、ymax、zmin、zmax)。然后根據坐標軸上這6個值處的垂直平面,構建一個包含該軌跡片段的長方體,再對長方體膨脹一定體積,將周圍較近的障礙物囊括進來。這樣根據該長方體及其所包含的障礙物信息就可以構建局部的ESDF。 在優化中實施了兩步優化機制,即將軌跡優化問題分解成空間和時間上的優化,該機制的效果已在文獻[16]中得到驗證。時間上的優化就是通過對時間參數的設定來限制無人機的速度和加速度,也就是本文所謂的時間分配。為了減少重復的工作,在優化中只需要對軌跡在空間上的位置進行限制,時間參數和無人機速度則被設置為常量,構建如下目標函數: ming=β1gs+β2gc (10) 式中:gs為加強軌跡平滑性的平滑項;gc為限制軌跡碰撞保證安全性的碰撞項;β1和β2為權重,實驗中分別設置為2.0和1.5。 本文將平滑項gs表示成加速度二階導數的形式,即軌跡fμ(t)的4階導數的平方對時間t的積分,具體形式如下: (11) 式中:[ti-1,ti]為局部軌跡片段的時間范圍;fμ(t)為m段n階多項式(實驗中n=5),m為該局部的關鍵點個數減1,即每段多項式表示相鄰關鍵點間的軌跡段。 碰撞項采用可微函數c(·)沿航跡弧長的線性積分來表示,同時本文將c(·)設計成指數函數,即 c(dp(t))=αe-γ(dp(t)-d0) (12) 式中:dp(t)為t時刻無人機的位置p(t)與最近障礙物的距離,由所構建的ESDF直接獲得;d0為安全距離閾值;α為函數的幅值;γ為變化率。根據該函數c(·),當無人機與最近障礙物的距離小于安全距離d0時,函數值能迅速變得很大,使碰撞項成為整個目標函數的主導項;而當距離大于d0時,函數值趨于平緩且相對較小,這樣就能使軌跡與障礙物保持安全距離。因此gc的具體形式如下(為了方便計算,積分最終離散化為求和形式): (13) 其中,l為該軌跡段的長度,Ti=ti-ti-1為該軌跡段的時間參數,Γk=ti-1+kδt為離散的時間變量,v(·)為無人機某時刻的速度。 上述平滑項和碰撞項的具體二次型形式和它們的雅可比矩陣推導可參考文獻[1],這里不再贅述。而對于該優化問題的求解,本文采用凸可分近似算法(CCSA)[21]。該算法不僅適用于大量變量的優化,而且能保證從任何起始點開始都能收斂到某個局部最小值。 (14) 因此第j段的速度貝塞爾曲線可由式(8)推得 (15) 同理,第j段的加速度貝塞爾曲線可由速度貝塞爾曲線的速度特性推得,這里不再贅述。根據速度和加速度貝塞爾曲線可知,時間參數越小,無人機速度和加速度越大,完成相應軌跡的飛行所需時間越短,但由于無人機有最大速度和加速度的限制,每個時間參數理論上都有一個最小值。 經過簡單平滑處理和局部優化后,本文方法獲得的軌跡是由低階多項式(1階、2階)和高階多項式(5階)組合表示的,因此設計了包含低階和高階時間分配的方法。本文先實現高階時間分配再實現低階時間分配,這樣約束較多的高階時間分配可以避免考慮相鄰軌跡段間速度連續的問題。在高階時間分配中,本文直接采用文獻[16]的時間分配框架,調整了該框架的輸入輸出,其中以軌跡段的控制點位置、初始時間參數、最大速度和最大加速度為輸入,以最優時間參數、該軌跡段起點初速度和終點末速度為輸出。 在低階時間分配中,軌跡段主要包含表示直線的1階貝塞爾曲線和表示直線間小段彎弧的2階貝塞爾曲線,其中2階曲線較短,只需為其設置相對合理的時間參數、初速度和末速度。而對于直線段軌跡,它的長度ds如圖4所示,往往接近或大于a個航點間距,足以為其劃分出3個區域:加速區、勻速區和減速區。因此本文重新表示該軌跡段,其中加速區和減速區用2階貝塞爾曲線表示(有加速度,階數必須大于1),勻速區用1階貝塞爾曲線表示,而且它們的控制點都在該直線上。這樣無人機在該直線段軌跡上先從初速度vs加速到最大速度vm進行勻速飛行,再減速到末速度ve進入下一段軌跡,其中加減速時的加速度為最大加速度am,vs、ve由與該直線段相鄰的曲線段在前面所述的時間分配后提供。然后計算得到加速區、勻速區和減速區的長度d1、d2、d3及對應的時間參數t1、t2、t3(d為該直線段總長): (16) 最后根據這些已知量和式(15),可以求得表示這3個區域的多項式中控制點的具體位置。另外,若無人機飛行中發生重規劃,那起點處是有初速度的。大部分情況下只需在重規劃的時間分配中加入初速度限制即可,但若初速度較大且方向與重規劃后的軌跡方向誤差較大,本文考慮讓無人機降速至0再進行重規劃。 本文基于機器人操作系統(ROS)框架和C/C++語言實現規劃方法。實驗平臺配置如下:處理器為Intel(R) Core(TM) i5-6500(3.20 GHz×4),內存為16 GB,系統版本為Ubuntu 18.04。實驗中采用了文獻[9]開源的四旋翼模型,其輸入為當前時刻t的位置、速度和加速度向量,這些輸入量可從規劃方法所生成的軌跡及其相應的表達式獲得。模型感知范圍是以模型為中心的圓,感知半徑可人為設置。地圖是障礙物隨機分布的三維場景(50 m×50 m×6 m)。實驗從單次規劃和多次規劃兩種情況對本文方法進行測試,最大速度和加速度分別為2 m/s和2 m/s2,數據都是30次實驗的平均值,其中關鍵點數為Nk,軌跡長度為L,飛行時間為tf,軌跡合格率為R,規劃時間為tg(包括了ESDF時間tESDF和前后端時間tba),障礙物數為No,飛行距離為df,規劃次數為Ng,規劃總時間為tg,t。 3.1.1 單次規劃的性能測試 表1 單次航跡規劃的性能測試結果Table 1 Performance test results of single trajectory planning 表2 不同轉彎代價權值下的測試結果Table 2 Test results under different turn cost weights 圖5 單次航跡規劃效果Fig.5 Effect of single trajectory planning 3.1.2 多次規劃的性能測試 未知環境是指無人機還未感知的環境。當目標點在較遠的未知環境中,無人機飛行時感知的環境會不斷更新(仿真中更新頻率為50 Hz),若已規劃出來的航跡碰到更新后的障礙物就會進行重規劃,因此需要多次規劃才能到達目標點。在實際應用中,無人機感知范圍有限(一般在20 m以內,實驗中設置為10 m),目標點距離往往較遠,故對規劃方法在長距離中實現多次規劃的性能測試是有必要的。文獻[1]方法由于需要構建全局ESDF,在更長距離的規劃中效率極低,很難達到實時要求,因此采用本文方法與當前經典且開源的硬約束法[9](兩者單次規劃效果差距不明顯)分別做了障礙物數為250、500和750的3組實驗(規劃距離約為40 m),結果如表3、圖6和圖7所示。從表3中可知,無論哪組實驗,本文方法的飛行距離、規劃效率(規劃總時間和次數)和飛行效率(飛行時間)均優于硬約束法。在飛行距離方面,因為硬約束法的前后端都沒有對軌跡長度加以限制,其后端中也是全局構建飛行走廊,在未知環境中容易生成冗余的軌跡(如圖6(a)所示),在重規劃前,無人機會按該冗余軌跡飛行,而本文方法的前端能搜索出最短路徑,且后端只進行局部優化,未知環境中基本上是直線軌跡(如圖6(b)所示)。從圖7(a)可知,本文方法的整個飛行航跡明顯比硬約束法簡短,轉彎幅度也小很多。在規劃效率方面,因為未知環境中軌跡越長,撞到更新后的障礙物概率越大,規劃次數也越多,同時,軌跡合格率較低也會使規劃次數增加。雖然硬約束法的單次規劃效率可能更高,但由于其規劃次數多,故規劃總時間要多于本文方法。在飛行效率方面,除了飛行距離的優勢外,本文方法的最大優勢是時間分配的合理性,曲線段和直線段軌跡都采用了高效的時間分配,如圖7(b)所示,本文方法盡可能利用最大加速度進行加減速,讓無人機在直線段軌跡中更多地進行最大速度的勻速飛行,而硬約束法利用速度場獲取相對合理的時間參數,過于保守。在軌跡合格率方面,因障礙物較少,兩種方法的效果都很好,但隨著障礙物的增加,硬約束法的合格率會下降得更快,因為飛行走廊只是邊界約束,允許軌跡貼近該邊界(即貼近障礙物),而本文方法前端加入安全距離約束,后端對障礙物密集的地方進行軟約束優化進一步加強安全性,軟約束通過構建ESDF所帶來的安全效益要優于飛行走廊。不過如果障礙物個數超過1 000,關鍵點數增加,局部構建ESDF的范圍也會變大,軟約束優化的效率和精度也會明顯下降。 表3 多次航跡規劃的性能測試結果Table 3 Performance test results of multiple trajectory planning 圖6 不同規劃方法生成的航跡對比Fig.6 Comparison of tracks generated by different planning methods 圖7 兩種方法的無人機航跡、速度對比Fig.7 UAV track and speed comparisons of two methods 本文搭建圖8所示的四旋翼平臺。該平臺配備了一個英偉達Jetson TX2,它包含一個由256個CUDA內核組成的圖形處理器,有8 GB的隨機存儲內存和32 GB的eMMC存儲空間。本文將PX4的開源硬件Pixhawk2用作飛行控制器,并通過UART接口將TX2的無人機控制命令發送給Pixhawk2,實現飛行控制。本文在TX2中構建了Ubuntu 16.04操作系統并基于ROS框架實現圖1所示的航跡規劃框架。本文還搭建了圖9所示的室內場景,障礙物大小相同且都是長方體。本文只測試航跡規劃的效果,所以每次飛行前地圖通過1∶1人工構建,四旋翼起點和終點在地圖中固定,相距約8 m,只需進行單次規劃。對于規劃方法生成的航跡,本文采用幾何控制器[22]進行跟蹤。另外,四旋翼飛行中可通過雙目相機獲取其與障礙物的距離來檢測航跡規劃算法的安全性。光流模塊則用于室內定位。 圖8 四旋翼平臺Fig.8 Quadrotor platform 飛行中設定最大速度和加速度分別為0.5 m/s和0.5 m/s2,本文方法的室內航跡規劃效果見圖9,虛線框內為局部優化后實現的曲線飛行,實驗中四旋翼無碰撞到達終點,且始終與障礙物保持一定的距離,其tESDF和tba分別為0.095 s和0.150 s。另外,本文統計了不同障礙物數下的飛行結果,如表4所示,每個數據都是進行20次飛行的平均值,其中r為曲線占比。從表中可知,隨著障礙物的增加,后端優化后的曲線占比也增加,這保證了軌跡合格率始終在0.9及以上,并且四旋翼按合格軌跡飛行時無碰撞發生,但軌跡長度和飛行時間也有所增加。該結果證明了本文方法可根據障礙物疏密程度切換直線和曲線兩種飛行模式,其中直線飛行速度接近0.4 m/s,而曲線飛行速度低于0.3 m/s,這樣能同時保證較高的飛行安全性和飛行效率。 表4 四旋翼室內飛行結果Table 4 Results of quadrotor indoor flight 針對無人機長距離航跡規劃效率不高的問題,本文提出了一種基于局部軟約束優化的實時無人機航跡規劃方法。該方法分為前端和后端兩個階段:前端通過安全距離約束和轉彎代價函數改進Theta*算法,獲取高質量的初始路徑;后端設計局部優化策略減少優化工作,并對局部質量不高的軌跡片段進行軟約束優化加強安全性和平滑性,然后根據貝塞爾曲線的速度特性實現高效的時間分配,以提升飛行效率。實驗結果表明:本文方法克服了前期工作中無法實現高效的長距離規劃問題;與現有的經典硬約束法相比,在約40 m距離的飛行中,本文方法的無人機飛行距離要短3 m左右,飛行時間少7 s多,規劃總時間少0.5 s以上。實際的室內飛行實驗也驗證了本文方法在真實系統中的適用性。 本文方法提升了無人機的整體飛行速度,但其安全性只在靜態環境中有保障,對于動態環境中高速飛行的緊急避障性能還有待提高。在今后工作中,可以考慮采用精度更高的B樣條曲線來表示航跡,利用其局部修改性質來避免全局重規劃,以提升整體規劃效率,完善緊急避障功能。2.2 局部軟約束優化
2.3 時間分配
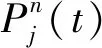
3 實驗及結果分析
3.1 仿真實驗

3.2 室內飛行實驗


4 總結與展望

