泛系拓撲與粗糙集
2022-07-08 07:20:40王曉艷馬驥
電子技術與軟件工程
2022年2期
王曉艷 馬驥
(1.山西工程科技職業大學 山西省晉中市 030619)
(2.中國能源建設集團山西省電力勘測設計院有限公司 山西省太原市 030000)
1 引言
1.1 經典粗糙集理論的基本概念
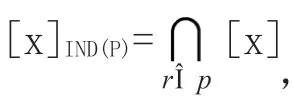

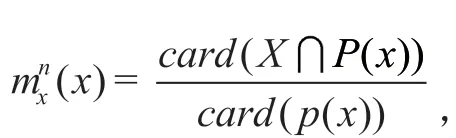
可見,給定知識庫K(U,R),對于每個子集X U和一個等價關系R∈ind(K),可以根據R的基本集合的描述來劃分集合X。為了衡量{des(Yi): Yi∈R}精確地說明X中對象的隸屬情況,考慮兩個子集:
R_(X)=∪{Y∈U/R:Y X}
R—(X)=∪{Y∈U/R:Y∩X≠?}
分別稱它們為X的R下近似集和R下近似集。集合bnR(X)= R—(X)-R_(X)稱為X的R邊界。
通常把posR(X)=R_(X)稱為X的正域,把negR(X)=R—(X)稱為X的R負域,把bnR(X)稱為X的邊界域。
正域posR(X)或X的下近似是那些對于知識R能完全確定地歸入集合X的對象的集合。類似地,negR(X)是那些對于知識R毫無疑問不屬于集合X的元素的集合,它們是屬于X的補集。邊界域是某種意義上論域的不確定域,對于知識R屬于邊界域的對象不能確定地劃分是屬于X或是-X。X的上近似是由那些對于知識R不能排除它們屬于X的可能性的對象構成的,從形式上看,上近似就是正域和邊界域的并集。
關于粗糙集理論的詳細描述請參見文獻。
1.2 泛系理論
泛系理論是研究廣義系統的學科。廣義系統可看成廣義硬件與廣義軟件的復合體或軟硬兼設體,這里廣義硬件可以是任何事物集,包括是另外的廣義系統或廣義軟件集,而廣義軟件則是有關的某些關系或帶參量的關系以及它們的迭代生成。形式上,可以定義廣義系統:((廣義硬件,廣義軟件))。廣義硬件:(任何事物集;任何廣義系統集;任何廣義軟件集);廣義軟件:(廣義硬件與參量的泛權關系族;廣義硬件與參量的泛系關系族;……
登錄APP查看全文
猜你喜歡
工業設計(2022年8期)2022-09-09 07:43:20
軍民兩用技術與產品(2021年10期)2021-03-16 06:05:30
海峽姐妹(2020年9期)2021-01-04 01:35:44
北京測繪(2020年12期)2020-12-29 01:33:58
VOGUE服飾與美容(2020年9期)2020-09-02 14:47:26
裝備制造技術(2019年12期)2019-12-25 03:06:46
中國洗滌用品工業(2019年4期)2019-05-11 09:27:34
家庭影院技術(2017年9期)2017-09-26 03:41:45
山東青年(2016年1期)2016-02-28 14:25:25
當代修辭學(2014年3期)2014-01-21 02:30:44

