散斑能見度光譜法測量筒倉內顆粒流的顆粒溫度

陳泉，鄭澤希，李然，3，孫其誠，楊暉

（1 上海理工大學光電信息與計算機工程學院，上海 200093； 2 上海理工大學機械工程學院，上海 200093； 3 上海理工大學醫療器械與食品學院，上海 200093； 4 清華大學水沙科學與水利水電工程國家重點實驗室，北京 100084）

引 言

筒倉作為常見的顆粒物料存儲設備廣泛應用于糧食存儲、醫藥加工和化工生產等領域[1-4]。理想的筒倉能夠在最小的占地面積上存儲最多的顆粒，并且以所需的質量流率正常流出[5]。然而，在運行時，由于離散顆粒的無序運動導致了筒倉內固體顆粒無法按照質量流（mass flow）形式正常流出，引起了筒壁與顆粒之間的黏滑運動[6]，間歇性堵塞[7]以及非局域流變[8]等問題。這些問題嚴重影響了產品的生產質量，甚至危害筒倉的安全運行。因此，測量筒倉內顆粒的無序運動，掌握其變化規律，在筒倉設計和化工調控工程中具有重要意義。

顆粒溫度（granular temperature）反映了介尺度條件下顆粒運動的無序程度[9]。Ogawa 等[10]根據微觀粒子的熱運動提出了顆粒溫度的概念來表征顆粒系統的無序運動，用δv2～<δvδv>表示，其中δv表示無規則運動顆粒的速度波動，<>表示系綜平均。顆粒溫度與熱力學溫度相似，二者都產生壓力，并且控制著顆粒系統的質量、動量和能量傳播。近20年來，人們采用離散單元法（discrete element method，DEM）對筒倉內顆粒流的顆粒溫度進行了大量研究，建立了介觀顆粒溫度與宏觀顆粒流型、質量流率之間的關系模型。2007 年，Ahn[11]采用基于硬球接觸模型的DEM 方法模擬不同質量流率條件下圓柱形筒倉內球形顆粒的運動，根據顆粒的矢量速度計算了筒倉內顆粒溫度的軸向分布，揭示了顆粒動能的耗散率與顆粒溫度值滿足指數為1.5 的冪函數關系。2013 年，Tewari 等[12]采用基于顆粒動理學的DEM 方法模擬二維筒倉中球形顆粒的運動，探究堵塞前顆粒流的動力學特征。根據單位時間步長內顆粒的位移計算出筒倉內顆粒流的顆粒溫度，發現了當質量流率較高時，筒倉中心區域的顆粒溫度值較低；而當顆粒流接近堵塞時，顆粒溫度的分布發生了明顯逆轉，在筒壁處的顆粒溫度存在極小值。2015 年，Regele 等[13]采用基于靜摩擦接觸模型的DEM 方法模擬球形顆粒通過具有狹窄通道的三維筒倉，統計了單元顆粒的平移速度和旋轉速度，計算了不同流態區域的顆粒溫度分布。研究表明：孔口附近快速顆粒流區域內存在較低的顆粒溫度值，但該位置處顆粒的旋轉速度較高。擴散波光譜技術（diffusing wave spectroscopy，DWS）和散斑能見度光譜技術（speckle visibility spectroscopy，SVS）是兩種能夠直接測量顆粒溫度的方法[14]。DWS 技術要求被測量顆粒系統的運動狀態具有穩定性，以滿足光子在自相關時間內的擴散傳播過程；SVS 技術是在DWS技術基礎上發展起來的，該測量技術的優勢在于具有良好的魯棒性，適用于筒倉內復雜顆粒流的顆粒溫度測量，并且SVS 技術具有微秒級時間分辨率(由線陣CCD相機的采集幀率決定,最快可以到10 μs)和微米級空間分辨率(激光波長的1/4，約0.1 μm)。2005 年，Bandyopadhyay 等[15]根據擴散波光譜法首次提出了散斑能見度光譜技術，并應用于振動流化床的顆粒溫度測量，觀測到顆粒溫度的測量值與系統振動頻率具有相同的周期性，進而驗證了該技術能夠準確測量密集顆粒系統的無序運動。2010 年，Katsuragi 等[16]利用散斑能見度光譜技術測量了斜坡流中不同位置的顆粒溫度分布，通過對比顆粒溫度與顆粒堆積密度，發現了顆粒溫度隨顆粒堆積深度的變化是非線性的。2019 年，本課題組[17-19]應用該技術測量了轉筒內雪崩顆粒流的顆粒溫度，觀察到雪崩前顆粒堆積的重排現象，發現了不規則顆粒的重排運動可以減小雪崩的持續時間。

因此，本文采用散斑能見度光譜技術，對卸料過程中筒倉內兩種粒徑的球形顆粒分別開展顆粒溫度測量。探究了穩態流動過程中顆粒溫度的分布特征以及顆粒粒徑對顆粒溫度的影響。最后，分析了堵塞過程中顆粒溫度的變化規律。

1 實驗材料和方法

為了掌握筒倉內顆粒流的復雜動力學，本文搭建了基于線陣CCD 相機的散斑能見度光譜實驗裝置，測量筒倉內玻璃珠在卸料過程中的顆粒溫度。

1.1 顆粒材料

圖1(a)是顯微鏡下均值粒徑為0.94 mm 的玻璃珠顆粒。由于透明材料可以幫助觀察顆粒床中一定堆積深度（4～6 mm）的顆粒運動，因此采用透明玻璃珠進行筒倉內顆粒流的測量實驗。首先，采用標準篩網（孔徑分別為0.88 和1.00 mm；孔徑分別為1.40 和1.70 mm）對玻璃珠進行了兩次篩分處理，獲得了兩種不同粒徑的實驗樣品顆粒。然后，隨機取出部分樣品顆粒放置在顯微鏡（Olympus SZX16）的工作臺上，放大25 倍后進行圖像采集。最后，根據顆粒的投影面積計算顆粒的等效圓面積直徑[20]。連續統計300 顆玻璃珠樣品，獲得實驗顆粒粒徑的累積分布，如圖1(b)所示。表1為兩種粒徑玻璃珠的特征參數。表中β是顆粒堆積的下休止角[21]。

表1 實驗顆粒材料的特征參數Table 1 Characteristic of granular materials used in this work

圖1 實驗玻璃珠的圖片和顆粒粒徑的累積分布(fCDF代表顆粒粒徑的累積分布函數；d代表顆粒粒徑)Fig.1 The image of glass beads and the cumulative particle size distributions of the glass beads

1.2 實驗裝置系統

圖2為實驗裝置實物圖。實驗裝置系統包括激光光源，凸透鏡，線陣CCD 相機，濾光片，電子天平秤和矩形筒倉。光源是波長為532 nm 的半導體激光器，輸出功率為100 mW，光束直徑為2 mm。出射激光經凸透鏡擴束得到直徑為8 mm 的入射光束。當入射光與堆積顆粒發生相互作用時，產生的前向散射光被線陣CCD 相機（加拿大DALSA 的Spyder mod 3）捕獲。線陣CCD 相機的像素尺寸為14 μm×14 μm，像元個數為1024 個，采樣幀率設置為20 kHz。為了減弱其他光源信號對實驗測量結果的影響，在線陣CCD相機的表面粘貼了532 nm的窄帶濾光片。平底矩形筒倉由長方體容器和金屬底座兩部分組成。長方體容器采用透明有機玻璃材料加工制成，壁厚為10 mm，高度和寬度分別為240 和150 mm，前后壁面的間隙為8 mm。筒倉底座由金屬鋁加工制成，表面采用電鍍工藝進行氧化黑處理。孔口矩形槽的寬度為8 mm，利用可調插銷控制孔口矩形槽的長度D1，使得D1在[4 mm,18 mm]范圍內變化。電子天平秤（SF-400）通過RS232 接口與計算機相連接，用于記錄筒倉內填充顆粒的質量流率。電子秤的最大采樣頻率為5 Hz，重復性誤差為1 g。以O點為坐標原點建立笛卡兒坐標系，其中，O點位于孔口中心的內壁上，x軸與y軸形成的平面與筒倉的前壁面平行，如圖2 中矩形筒倉的正視圖所示。平底矩形筒倉是關于中心垂線對稱的，因此在x?[0,75 mm]，y?[0,240 mm]范圍內測量顆粒溫度。每個測量點的大小為直徑8 mm 的圓形區域（約40 個顆粒），兩個相鄰測量點之間的中心距離為10 mm。測量點A位于筒倉孔口附近的快速顆粒流區域。測量點A為直徑8 mm 的圓形區域，中心坐標為A(0,10 mm,0)。實驗前，先利用軟橡膠塞堵住孔口矩形槽，再從筒倉頂部采用均勻分散加載方式進行玻璃珠的加載。

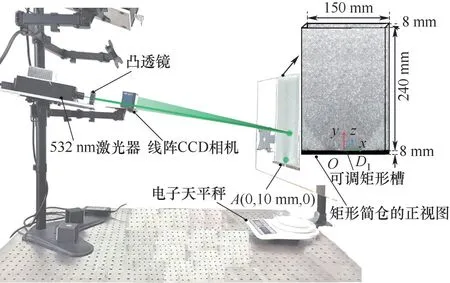
圖2 實驗裝置實物圖(D1代表筒倉孔口的長度)Fig.2 The annotated photo of the experimental setup

1.3 散斑能見度光譜法

圖3為散斑能見度光譜法測量顆粒溫度的原理圖。假設單個光子通過離散顆粒樣品時發生了N次散射，則根據擴散波光譜原理，在t時刻光子散射N次的總路徑長度S為[22]

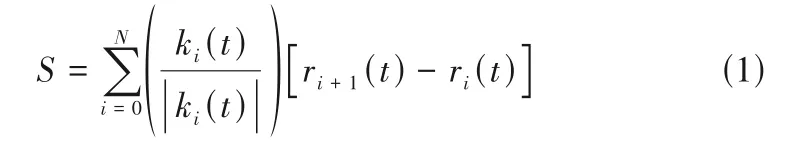
式中，ki(t)為t時刻光子經過i次散射后的波矢量；ri(t)為t時刻顆粒的空間位置坐標。同時，光子的相位可以表示為[23]

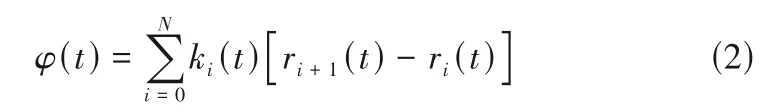
式中，φ(t)為光子相位隨時間的變化函數。根據式（1）和式（2），得到散射光強E(t)的表達式為

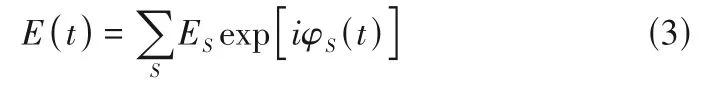
式中，ES為光程為S光子的光強幅值。

因此，散射光場的歸一化自相關函數可以表示為

式中，λ為入射激光的波長；δv= <δv2>，δv2表示顆粒溫度；Γ= 4πδv λ，是函數g1(t) 的衰減線寬。

根據統計光學原理，散斑圖像的對比度可以用單位曝光時間內散射光強的方差σ與均值的比值來表示[24],即

式中，T為采集相機的曝光時間。根據高斯光束的Siegert 公式，建立了散斑圖像對比度與散射光場自相關函數之間的關系[25]

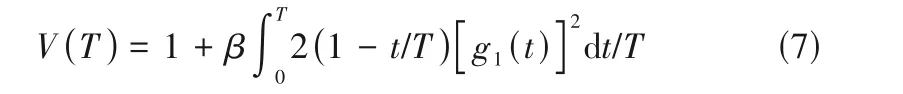
式中，β為測量系統的相干因子。將式（5）代入式（7），得

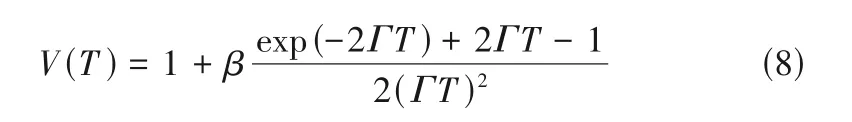
顆粒溫度可以根據式（8）反演獲得。注意，由于受到CCD 相機的電路噪聲和測量環境的干擾，相干因子β無法被準確測量[15]。為了解決該問題，一般將2 倍和1 倍曝光時間下的散斑對比度值相除，消去系統相干因子，來獲得顆粒溫度δv2。另外，一般要求散斑面積的等效直徑約等于10 倍顆粒粒徑。

由于光子的波粒二象性，在測量區域內不同光子的傳播會產生干涉現象，從而在CCD 相機上顯示出“顆粒狀”的散斑圖像，如圖3 中灰度圖所示。在相同的曝光時間條件下，顆粒的運動速度越快，散斑圖像的模糊程度越高，而散斑圖像的對比度就越低。圖3 中紅色曲線是根據圖3 中的散斑圖像計算獲得的顆粒溫度變化曲線。散斑能見度光譜測量技術的重復性誤差小于3%[26]。

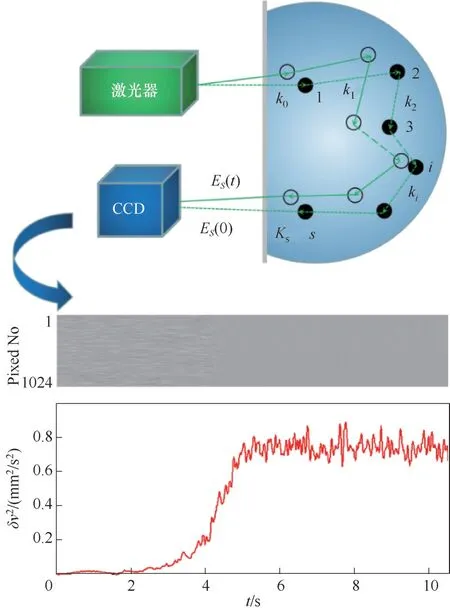
圖3 散斑能見度光譜法測量顆粒溫度的原理示意圖[ES(t)代表光程為S的散射光子在t時刻的光強幅值；ki代表入射激光經過i次散射后的波矢量]Fig.3 Schematic diagram of measuring granular temperature by speckle visibility spectroscopy

2 實驗結果與討論

設置孔口矩形槽的長度D1=12 mm，將均值粒徑為0.94 和1.55 mm 的玻璃珠加載到平底矩形筒倉內進行實驗。采用散斑能見度光譜法測量卸料過程中顆粒流的顆粒溫度，每個測量點重復測量10 次。由于筒倉內顆粒流的運動是關于筒倉中心軸線對稱的，因此在顆粒溫度測量過程中，僅測量筒倉內顆粒流的右半部分。

2.1 顆粒溫度的特征

圖4 為卸料過程中筒倉內測量點A的顆粒溫度變化曲線。可以看出，顆粒溫度曲線包含了初始瞬態流，穩態顆粒流和排空三種不同的卸料階段。在穩態顆粒流中，顆粒溫度值保持相對穩定。該結果說明了卸料過程中離散顆粒的運動在介尺度條件下具有穩定性；而在非穩態顆粒流中，由于顆粒介質之間的摩擦和非彈性碰撞具有高度的非線性[27]，導致了顆粒溫度曲線存在較大的梯度變化。另外，對比卸料過程中顆粒流的三種不同階段，穩態顆粒流的持續時間最長。因此，在接下來的研究中重點關注穩態顆粒流的顆粒溫度。

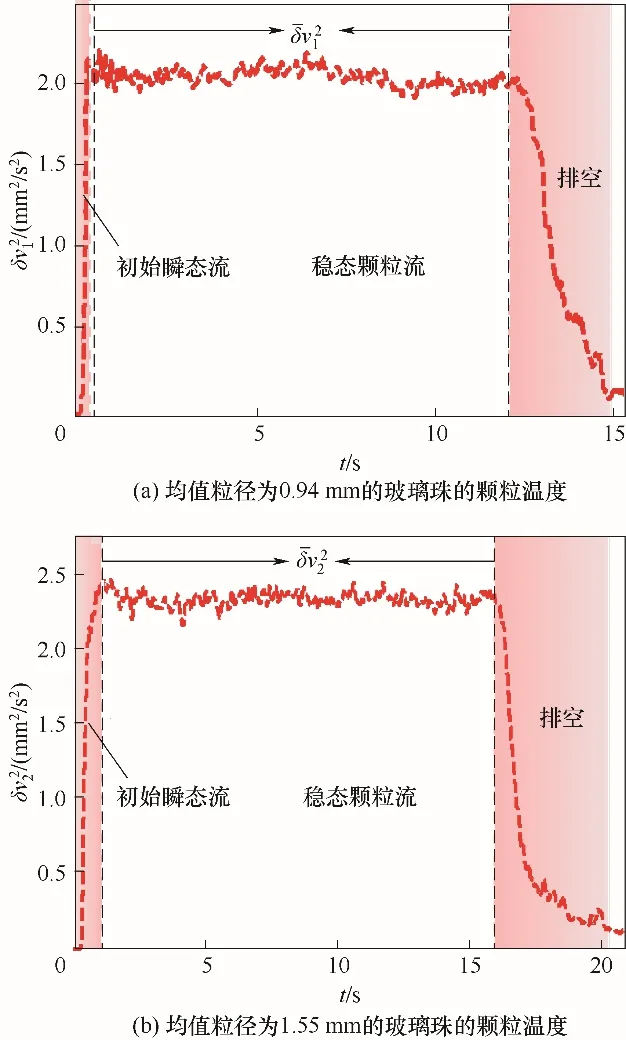
圖4 筒倉內顆粒流測量點A(0,10 mm,0)的顆粒溫度變化曲線(代表穩態流中粒徑為0.94 mm顆粒的平均顆粒溫度；代表穩態流中粒徑為1.55 mm顆粒的平均顆粒溫度)Fig.4 The curve of granular temperature at measuring point A(0,10 mm,0)in silo

表2 為穩態顆粒流過程中筒倉內A位置顆粒溫度與質量流率的均值和方差。可以看出，10 次實驗中顆粒溫度的測量結果具有良好的一致性。值得注意的是，均值粒徑為0.94 和1.55 mm 顆粒的質量流率分別為Q1=(33.5±0.8) g/s，Q2=(26.7±0.7) g/s；而顆粒溫度為δv21=(2.02±0.01) mm2/s2，δv22=(2.35±0.02)mm2/s2。這表明了大粒徑顆粒的無序運動程度更強，即大粒徑顆粒在卸料過程中具有更高的能量耗散，這可能是導致其質量流率較低的直接原因。該現象揭示了介觀顆粒的無序運動是控制宏觀質量流率的主要因素之一。在實際應用過程中，通過在筒倉內部添加障礙物調節離散顆粒的無序運動，可以為調控宏觀質量流率提供新的途徑。

2.2 顆粒溫度分布

圖5為兩種粒徑顆粒在筒倉內穩態顆粒流中的顆粒溫度分布。可以看出，不同粒徑顆粒的顆粒溫度分布具有相似性。顆粒溫度的最大值出現在筒倉頂部區域，并且以“收縮”形式向下遞減傳播，如圖5(a)和(b)所示。筒倉頂部的高顆粒溫度值可能是顆粒床的雪崩運動導致的。注意，兩種粒徑顆粒在筒倉孔口附近均存在一個低顆粒溫度區域。較低的顆粒溫度值揭示了該位置處離散顆粒存在定向有序的運動，這與斑團模型中介觀顆粒運動的特征相同，并且Zhang 等[28-29]在DEM 模擬實驗中也觀察到了類似的現象。進一步，根據Hu 等[30]的研究結果，筒倉孔口兩側的堆積顆粒可能是造成低顆粒溫度的直接原因。孔口附近停滯區的顆粒堆積可以減小離散顆粒間碰撞產生的接觸力，從而降低了顆粒系統的顆粒溫度。這表明在實際筒倉的優化設計中，孔口兩側添加緩沖單元，可以減弱顆粒間碰撞產生的接觸力，從而使得填充顆粒可以更容易排出，有利于減小筒倉的堵塞概率。

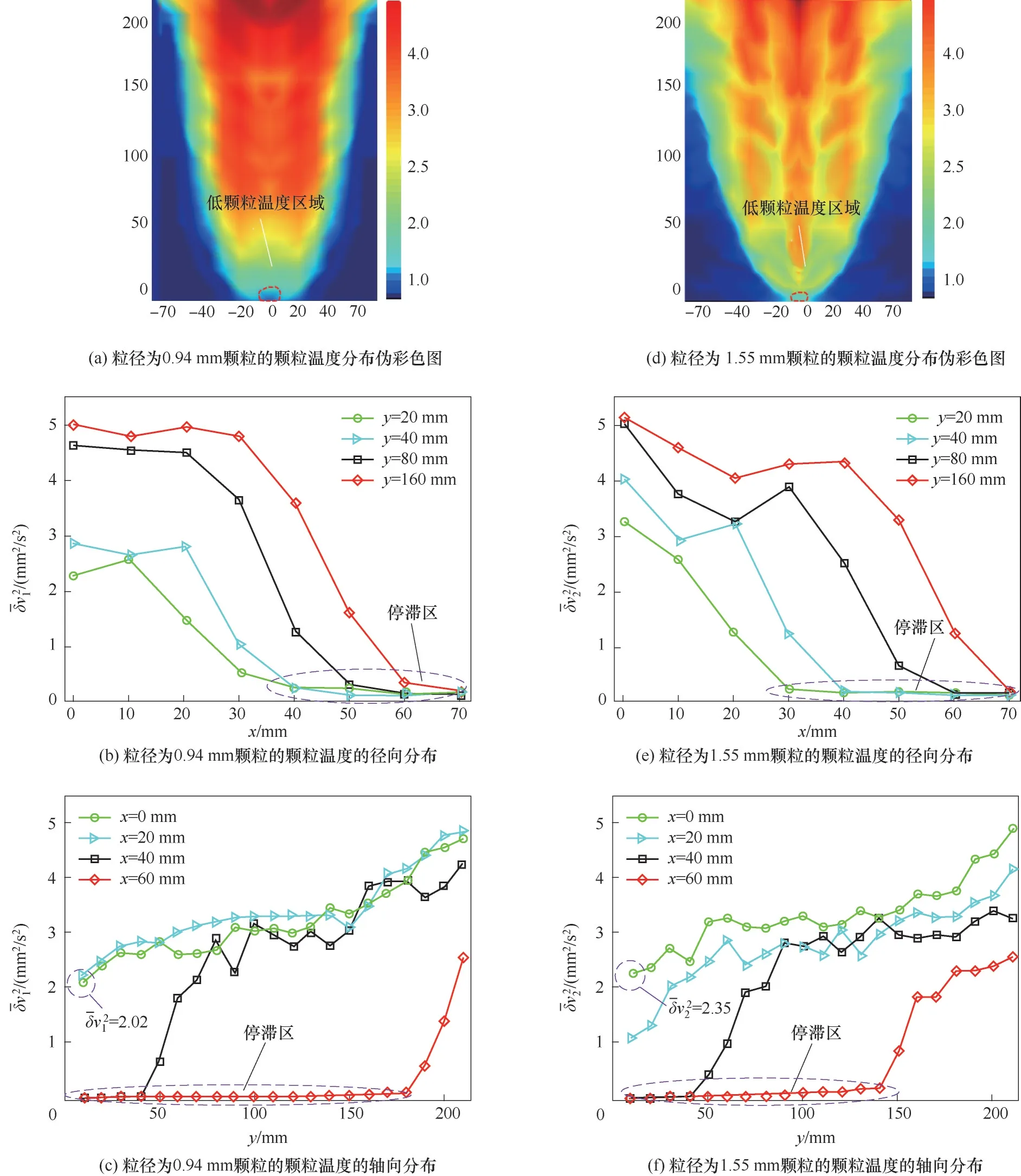
圖5 穩態流動中筒倉內顆粒流的顆粒溫度分布Fig.5 Granular temperature distribution of steady flow in silo

圖5(b)和(e)分別為均值粒徑為0.94 和1.55 mm顆粒的顆粒溫度的徑向分布。可以看出，兩種粒徑顆粒的顆粒溫度的徑向分布是基本相同的。在筒倉的不同高度y處，顆粒溫度的變化趨勢是一致的，顆粒溫度值隨著x的增大而減小。并且，隨著y值的減小，顆粒溫度為0 值的測量點逐漸增多。這表明了停滯區隨著筒倉高度的降低而增多。然而，在不同的軸向位置處，顆粒溫度的值隨著y的增大而增大，如圖5(c)和(f)所示。當測量點距離筒壁約10 mm時，顆粒溫度約為0值，這表明該位置處的顆粒均處于停滯區內。

2.3 顆粒流的堵塞測量

堵塞現象在筒倉顆粒流中是隨機產生的。圖6 為堵塞過程中筒倉內A位置的顆粒溫度變化曲線。可以看出，當t>0.06 s 時，顆粒流處于穩態流狀態，顆粒溫度值相對穩定，在2.02 mm2/s2上下波動。然而，當t=0.06 s 時，筒倉內顆粒流發生了堵塞現象。在0.06 s 時間內，顆粒溫度值從2.02 mm2/s2減小至0。這表明了筒倉內顆粒流的堵塞現象存在一個弛豫過程。進一步，在誤差小于2%的條件下，采用最小二乘法對堵塞前0.06 s 時間內的顆粒溫度進行擬合處理，結果如圖6 中插圖所示。可以看出，堵塞過程中的顆粒溫度變化滿足指數函數分布。

圖6 堵塞過程中均值粒徑為0.94 mm顆粒在筒倉內A位置的顆粒溫度變化曲線(插圖為堵塞前0.06 s時間內的顆粒溫度曲線；藍色實線代表擬合曲線；Δt表示堵塞過程的弛豫時間)Fig.6 The curve of granular temperature with an average particle size of 0.94 mm at position A in silos during blockage

圖7是筒倉內顆粒流堵塞過程的弛豫時間Δt隨孔口矩形槽長度D1的變化曲線。可以看出，在相同孔口尺寸條件下，均值粒徑為1.55 mm 顆粒的堵塞弛豫時間Δt更長。觀察到D1在[4 mm, 18 mm]范圍內時，兩種粒徑顆粒的堵塞弛豫時間Δt與孔口尺寸D1均滿足正比例關系，最短弛豫時間 Δt=（0.020 ±0.002）s。該結果表明通過測量筒倉內顆粒流的介觀顆粒溫度信號，可以提前預測顆粒流的堵塞事件，并且隨著筒倉孔口尺寸的增加，可以更早預測顆粒流的堵塞。

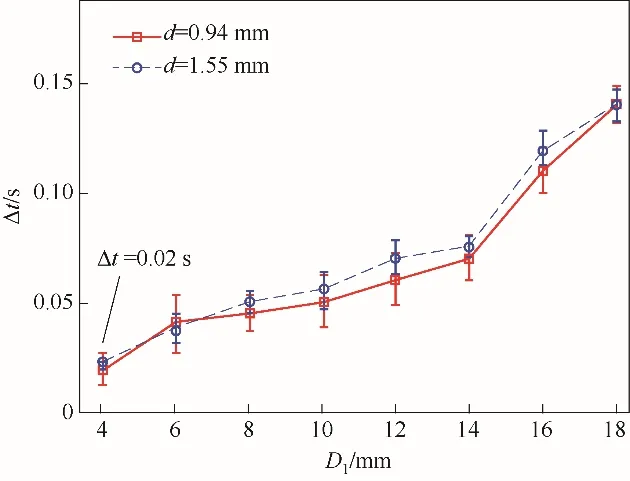
圖7 筒倉內顆粒流堵塞過程的弛豫時間Δt隨孔口矩形槽長度D1的變化曲線Fig.7 The curve of relaxation time of blockage changed with orifice size in silo

3 結 論

基于散斑能見度光譜技術對卸料過程中筒倉內顆粒流的顆粒溫度進行了測量，對比了均值粒徑為0.94 和1.55 mm 兩種玻璃珠的時變顆粒溫度，探究宏觀質量流率與介觀顆粒溫度之間的聯系。同時，利用該測量技術高時空分辨率的特點，分析了筒倉顆粒流堵塞過程的弛豫變化特征。主要結論如下。

（1）對比均值粒徑為0.94 和1.55 mm 顆粒在筒倉內穩態流動中的質量流率和顆粒溫度,發現了質量流率較大的顆粒，其顆粒溫度值較低。該現象揭示了介觀顆粒的無序運動是控制宏觀質量流率的主要因素之一。

（2）發現了筒倉孔口附近存在一個低顆粒溫度的特征區域，說明了該位置處的離散顆粒存在定向有序的運動。筒倉孔口兩側的堆積顆粒可以有效減弱顆粒間碰撞產生的接觸力是造成該現象的主要原因。

（3）不同粒徑顆粒的顆粒溫度分布具有一致性。顆粒溫度的最大值出現在筒倉頂部區域，并且以“收縮”形式向下擴散傳播。在筒倉的不同高度y處，顆粒溫度的變化規律是相同的，隨著x的增大而減小。然而，在不同的軸向位置處，顆粒溫度的值隨著y的增大而增大。

（4）利用散斑能見度光譜技術的高時間分辨率的特點，確定了筒倉內顆粒流堵塞的弛豫過程，發現了堵塞過程中的顆粒溫度變化滿足指數函數分布。并且弛豫時間與筒倉孔口尺寸呈正比例關系。該結果有助于揭示顆粒流隨機堵塞的預兆。

本文實驗結果揭示了筒倉內顆粒流的運動規律，為完善顆粒材料的傳輸效率和化工過程的精準控制提供了參考數據。