基于模擬退火算法的真實多孔電極中熱-質傳遞的研究

黃盼，練成，2，劉洪來，2

（1 華東理工大學化工學院，上海 200237； 2 華東理工大學化學與分子工程學院，上海 200237）

引 言

電場作用下電極中電化學反應-熱質傳遞現象是典型的多尺度問題[1-3]，如圖1 所示。微觀尺度(電子-離子遷移、晶格穩定性)、介觀尺度(界面熱/動力學、熱-質傳遞、電流電壓分布)和宏觀尺度(散熱性能、充放電管理)的傳遞和反應特性，直接決定系統中的濃度分布和反應速率，最終影響儲能轉化效率。而系統中發生傳遞和反應過程的場所主要在多孔電極中，且多孔電極的不規則表面引起的限域效應顯著影響著其內的傳質和傳熱過程，所以深入研究介觀尺度下多孔電極中的熱-質傳遞現象及其耦合機制，對高性能電化學儲能器件的設計有重要意義[3]。但是，與平板電極不同，對多孔電極中熱-質傳遞現象的研究存在兩個關鍵問題：一方面，多孔電極豐富的孔道體系、多樣化的表面形態和分布復雜的催化活性位點，難以用傳統數學工具去準確描述其結構[4-6]；另一方面，多孔電極中發生的過程涉及在受限空間中的離子遷移、熱量產生和傳遞、雙電層形成、電子傳遞的耦合，極大地影響了離子和熱量在孔道中的傳遞過程，并難以直接用實驗進行原位表征[7-8]。因此，多孔電極中的熱-質傳遞的研究一直以來都難以獲得突破性進展。

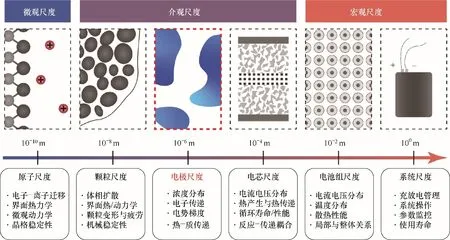
圖1 儲能和轉換過程中的電極尺度問題及與其他尺度問題的聯系Fig.1 The electrode scale issues in energy storage and conversion processes and their relation to other scale issues

目前，研究者們可以采用密度泛函理論(DFT)[9-10]和分子動力學(MD)模擬[11-12]等方法研究納米級多孔結構中的演化過程和充電機理。例如納米多孔電極與離子液體的結合是提高超級電容器能量密度的重要手段。然而，這總是伴隨著功率密度的降低，特別是考慮到高黏度和大空間位阻的離子液體。Gan 等[11]利用MD 模擬發現在閾電位作用下，具有疏離子孔的電極內的離子呈現出一種新的充電機制，即離子吸附。進一步得到了充電時間/電容與電壓/耐離子性能之間的定量關系，以評價協同提高超級電容器能量密度和功率密度的臨界條件。雖然DFT 和MD 模擬可以考慮微觀粒子間的作用力，但是受限于計算能力的瓶頸，只能模擬離子濃度和溫度在含周期性邊界條件的高度有序的納米級多孔結構(如分子篩和金屬有機框架)中納秒級的演化過程，并不能全面描述真實多孔電極中，尤其是常見的無定形碳電極中的離子和熱量的傳遞過程[9]。連續介質模型通過偏微分方程組描述離子濃度和電勢的狀態演化及其本構關系，可以建立納米級及以上空間尺度的復雜的多物理場耦合關系[13]。例如，Tao 等[14]采用基于Poisson-Nernst-Planck(PNP)方程和Navier-Stokes 方程的組合方法，通過控制氧化石墨烯膜的偏置角度，研究了不同層間距分布的氧化石墨烯膜中離子的輸運現象。d′Entremont等[15]從第一性原理推導出控制能量方程，并與修正PNP模型相結合，從而得到由于離子擴散、空間效應和混合熵的變化而產生的不可逆焦耳熱和可逆熱產生速率。但是，目前連續介質模型在多孔電極中的大規模運用仍存在兩個難點：準確描述多孔介質的復雜結構和快速求解含有復雜邊界條件的偏微分方程組。因此，多種簡化的多孔電極表示方法和經驗模型被廣泛運用。天然形成的和部分人工制造的多孔介質的微結構具有分形特征，可用分形維數表示。Sakaguchi 等[16]利用PNP 方程研究了分形多孔電極中的充電過程，并發現分形多孔介質充注過程的時間演化遵循冪律，指數與分形維數有關。目前大量研究都集中在單個孔隙中的充放電過程，因此可以通過等效介質近似(effective medium approximation,EMA)方法[17]，用假設的、具有相同導電性的單個孔隙組成的均質網絡來替代無序多孔介質的非均質網絡中的孔隙，同時保持孔隙網絡的連通性。Lian 等[18]利用該方法研究了平均孔徑、孔徑分布和孔連通性對多孔炭電極離子輸運特性(包括電導和電導率)的影響。更進一步地，孔隙網絡模型(pore network modeling, PNM)采用不同大小的球體和圓柱代表多孔結構中的空腔和吼道[19]。因此，PNM 可以考慮多孔電極中的孔徑分布和孔道連通性等性質，且計算成本非常低，可以在合理的時間內通過PNP 方程計算儲能設備的電化學性能和尋找最佳電極結構[20-21]。此外，Lian 等[8]報道了一種簡單且基于物理的堆疊電極模型來表示多孔電極，成功用PNP 方程和等效電路模型解釋了超級電容器的緩慢充電動力學，并發現充電過程可以分為兩個不同弛豫時間尺度的階段。雖然上述簡化的多孔電極模型被成功運用在解釋儲能過程中的各種現象，但這些方法只能在一定程度上接近真實的多孔電極的孔徑分布，很難表示多樣化的表面形態和分布復雜的催化活性位點，因此限制了這些簡化模型在多孔電極中的應用。

為了對真實的多孔電極(尤其是非均質、各向異性材料)中的熱-質傳遞過程進行深入的理解，需要對孔隙和骨架結構進行高分辨率三維表示。目前可以通過微尺度X 射線計算機斷層掃描[22-23](computed tomography, CT)或掃描電子顯微鏡[24](scanning electron microscope, SEM)以非破壞性的方式獲取多孔介質的孔隙結構。但是，CT不能分辨微米以下的結構，SEM 的缺點是它只提供二維信息。獲得多孔電極的三維結構表示的一種流行的替代方法是隨機重構。總地來說，隨機重構包括處理可用的信息，并生成符合所導出的介質特性的隨機結構兩個步驟。基本上有兩種重構方法。第一種依賴于基于流程的建模。這種方法試圖模擬自然材料在其原始環境中的形成過程[25]，或創造工程材料的過程[26]。然而，現有的基于過程的方法只考慮了某些方面，難以準確描述材料結構。一種試圖解決這些問題的方法是相場方法[27]。第二種類型的重構方法采用了一種更加數據驅動的方法，并使用了統計數據。這些統計數據主要來自通過圖像分割識別出孔隙相和骨架相的各類圖片，使用兩點統計信息，如自相關或概率函數[28]、線性路徑函數[29]和聚類函數[26]。最常用的兩點統計量重構方法是模擬退火(simulated annealing, SA)算法[30-32]。與可能非常復雜，并且可能需要大量超參數調優的基于多點統計[33]的方法相反，模擬退火算法的簡單性和準確性在實際運用中很有吸引力。Wu 等[34]采用SA 算法重構商業鋰離子電池陰極LiCoO2的三維微觀結構，包括活性材料相、孔隙相和添加劑相。重構陰極的表征提供了重要的結構和輸運性質，包括兩點相關函數、體積比表面積、曲折度和單個相的幾何連通性。Habte 等[35-36]研究了正極材料的微觀結構形態對鋰離子電池性能的影響，首先通過模擬退火算法生成了球形電極的結構，然后計算出結構參數并代入阻抗譜經驗公式中，最后得到的阻抗值與實驗結果符合較好。目前研究大多都停留在多孔電極的重構、孔結構參數[34,37]和等效傳遞系數[38-39]的計算上，真實多孔結構的形貌和孔隙結構對離子傳遞和電極導熱的影響尚未被研究過。

本文提出一套研究介觀尺度下真實多孔電極中的熱-質傳遞的研究框架：首先采用一種基于改進的狀態更新的隨機重建方法和動態退火系數相結合的模擬退火算法，將圖像分割后的二維SEM 圖重構為真實介觀尺度的三維多孔電極，重構生成的多孔電極的結構和真實多孔電極截面上的結構在統計學意義上是一致的，并在此基礎上建立真實多孔電極中的離子傳遞和電極導熱模型。

1 研究思路

本文的研究思路如圖2所示。通過改進的模擬退火算法和有限元計算，研究了真實多孔電板中的離子傳遞和電極導熱現象。

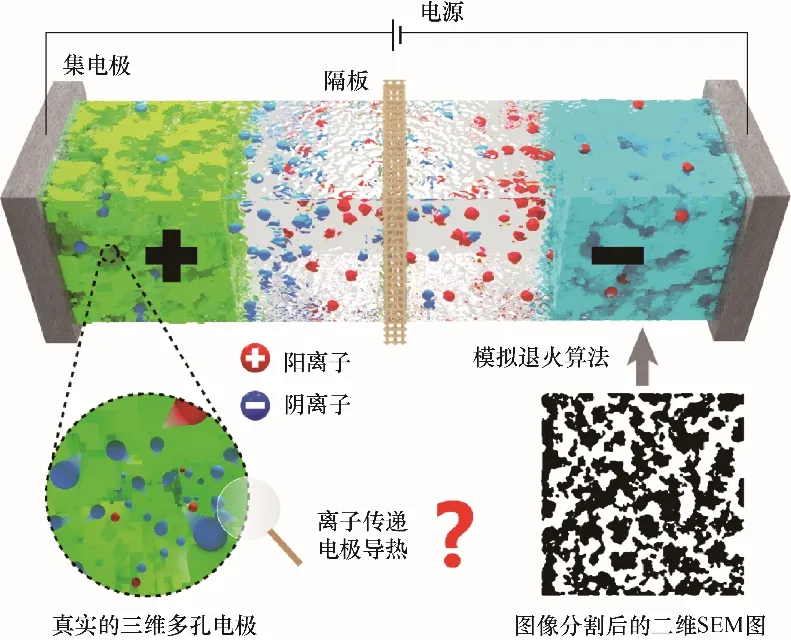
圖2 基于模擬退火算法重構的真實多孔電極中的離子傳遞和電極導熱Fig.2 The ion transport and electrode heat conduction in real porous electrode based on simulated annealing algorithm

2 真實多孔電極的三維重構及其結構參數計算

如圖3所示，多孔電極三維重構過程如下：首先利用SEM 掃描多孔電極，得到參考圖像；然后對其進行預處理，即通過圖像分割識別孔隙相和骨架相，得到二值化圖像序列，并將二值化圖像序列作為參考模型；然后生成與參考模型的孔隙率相同的隨機初始點云，利用改進的模擬退火算法進行隨機重構，將兩點相關函數作為優化目標，采用一種改進的體素交換方法更新狀態，得到重構的多孔電極的點云；最后將點云實體化為立方體構成的空隙相和骨架相的結構，并計算了其結構參數。

從表5三次考查結果可以看出，進入錫石浮選脫泥前-0.010 mm粒級產率為56.68%，含泥較高，經過三次脫泥后，有45.30%的錫金屬進入錫石浮選中，整個錫石浮選作業效率達到79.44%，對原礦的回收率為5.15%。超過了預期目標。

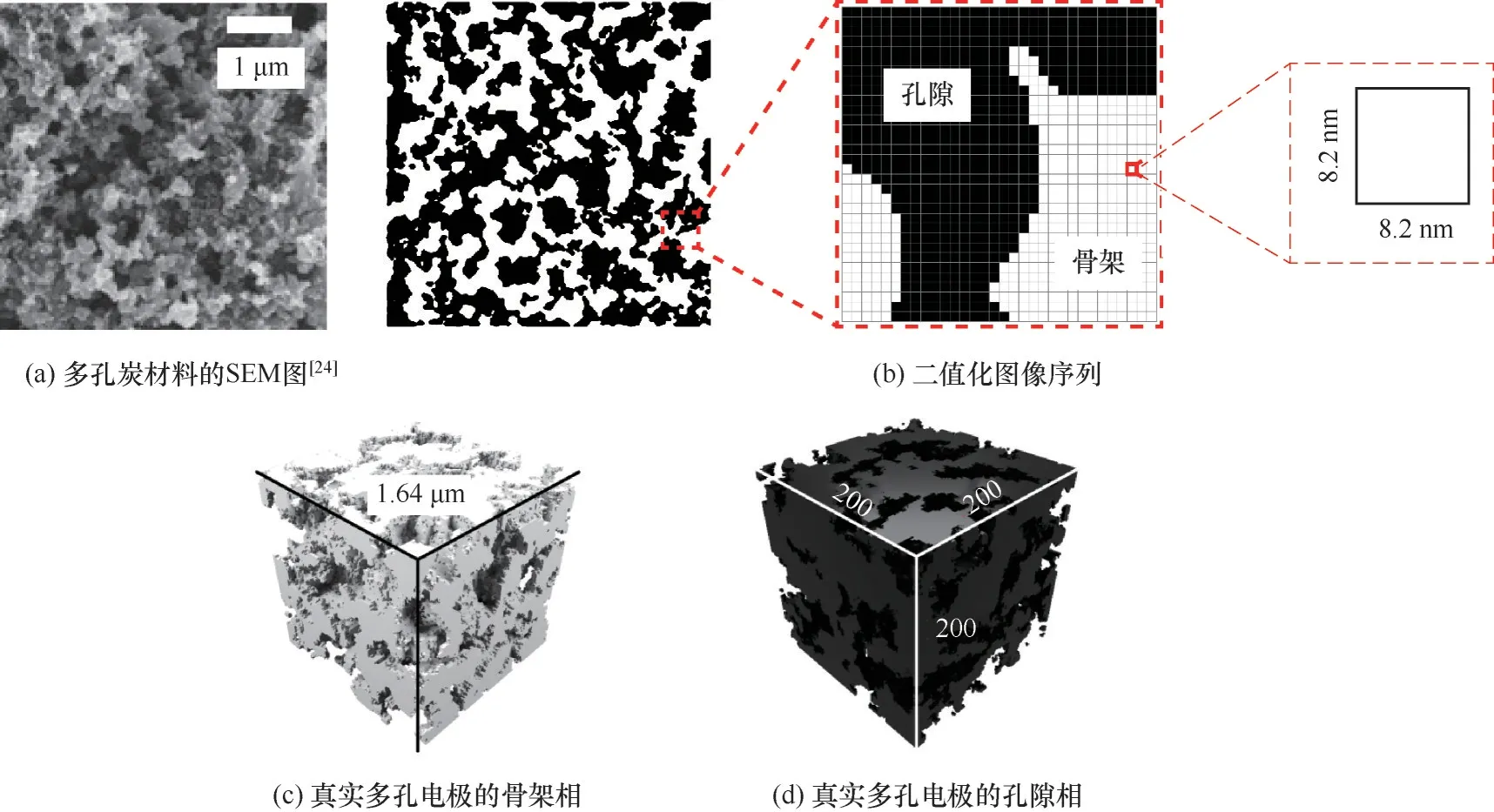
圖3 多孔電極三維重構流程圖Fig.3 The flow chart of three-dimensional reconstruction of porous media

2.1 圖像預處理

目前研究和應用較多的電極材料主要集中在多孔炭材料、過渡金屬氧化物和導電高分子等方面。其中多孔炭材料具有比表面積大、導電性好、結構穩定、資源豐富、價格低廉等優勢，既可直接作為電極，又可與其他材料復合，起到傳輸電子、舒緩體積膨脹以及優化界面反應等作用，被廣泛用為電極材料[40]。多孔炭材料的SEM 圖來自于Kunanusont等[24]的工作，如圖3(a)所示。他們采用超臨界二氧化碳干燥法，在10.0～20.0 MPa和40℃條件下制備了乙炔炭黑和聚偏氟乙烯基多孔電極，并研究了壓力對電極形態、孔隙率和電化學性能的影響。

通過SEM 掃描得到的灰度圖像序列中，孔隙相和骨架相的灰度值差異明顯。因此，首先通過閾值分割算法將灰度圖像序列轉化為只有孔隙相(黑色區域，灰度值為0)和骨架相(白色區域，灰度值為255)的二值化圖像序列。采用SEM圖中所有像素的灰度值的平均值(本文為144)作為閾值。當某處的灰度值高于閾值時，則將此處的灰度值設為255；當灰度值小于等于平均值時，則設灰度值為0。處理后的圖像中含有斑點噪聲和大面積的孔洞，采用形態學運算填充大面積孔洞，同時去除圖像中的雜質和亮斑等噪聲干擾[41]，從而得到預處理之后的二值化圖像序列，如圖3(b)所示。

2.2 圖像結構描述符計算

多孔電極的結構與其結構描述符密切相關，在對多孔電極重構時，需要考慮其結構描述符等信息，使重構模型與參考模型更加符合[42]。采用特征函數Ij r定義不同的結構描述符。在多相系統中，假設第j相所占的區域為Vj，其在系統中的濃度為φj，則第j相的特征函數為

攻城的鬼子是真瘋了，在天上飛機，地上大炮配合下，冒著大雨，從衢州火車站方向，對南門陣地接二連三發動了聯隊級別的攻勢。一千多米的扇面陣地上，血水染紅了整個表體，上千具日軍的尸體倒臥在泥漿地里。

2.3 模擬退火算法

在實際的多孔電極中，孔道的形態一般是彎曲的，離子的傳輸路徑總長度為l，一般遠大于電極的厚度H。曲折因子τ表示結構對擴散過程的影響程度，定義為τ=l/H。本文采用皮爾遜隨機行走模擬[48]來計算曲折因子。

2.3.1 模擬退火算法基本框架 圖4 是由Yeong等[31]首次提出的模擬退火算法運用在多孔介質重構中的基本框架。首先獲得參考模型w0[圖3(b)]的能量函數E(w0),設置初始溫度為T=T0。然后隨機產生與w0的孔隙率相同的初始結構w，并計算其能量函數E(w)。通過像素交換的方式產生新的結構w′，計算其能量函數E(w′)以及能量增量ΔE=E(w′) -E(w)。若ΔE< 0，則接受新結構，即w=w′,E(w) =E(w′)；否則以概率P= e-ΔE/T接受新結構。在當前溫度下新結構被多次拒絕后，通過退火過程降低溫度T，然后重新搜索最優結構，直到滿足算法的終止條件。

式中，ε0是真空介電常數，F·m-1;εr是相對介電常數；kB是Boltzmann 常數，J·K-1；T是溫度，K;e是基本電荷，C;ρbulk是體相離子數密度,m-3。由于在這個過程中離子電遷移導致電解液中的離子濃度不均勻，體系存在濃度梯度，所以充電過程中離子的運動還受到擴散的影響。

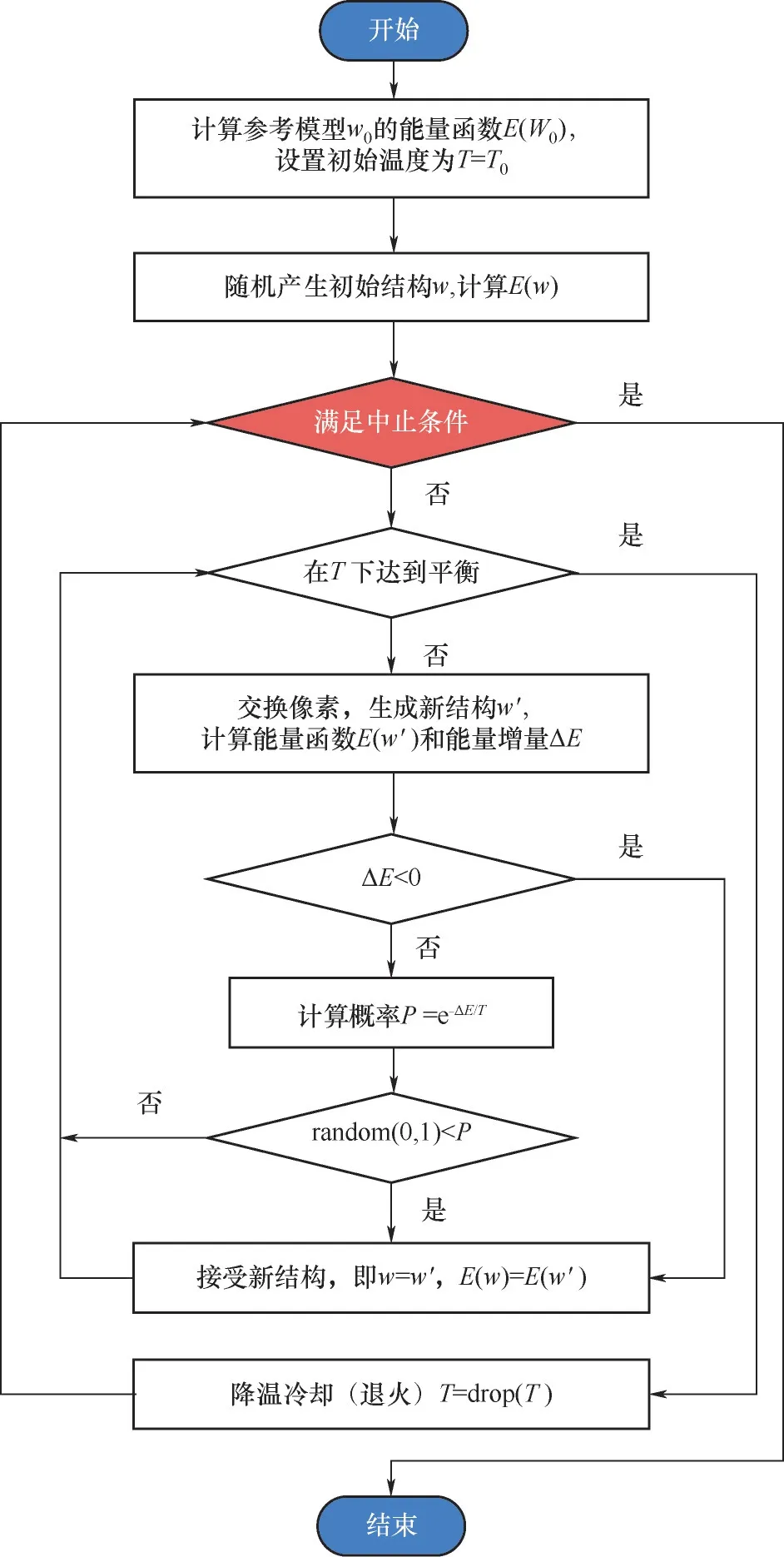
圖4 模擬退火算法流程圖Fig.4 The flow chart of simulated annealing algorithm

退出模擬退火算法的條件如下：①系統的能量函數小于閾值Eth；②相鄰兩步能量下降的絕對值小于ΔEth；③連續Ncon次結構無更新，即連續拒絕隨機產生的新結構Ncon次；④達到最大的迭代次數Niter。2.3.2 能量函數 原則上，任何結構描述符或描述符的組合都可以用來計算能量函數E。一般來說，定義E時考慮的描述符越多，計算量就越大，且過多描述符的加入并不能顯著提高重建質量。因此，本文僅使用S2和L2的組合S2-L2來計算E[31-32]。設能量函數E為重構模型與參考模型在各個方向上S2-L2的差值平方和的范數，計算方法為

如前所述，水資源作為公共商品與公共利益的實現密切相關。為了確保水資源分配實現推進公共利益的目標，水資源初始分配后通常面臨不斷調整的現實：滿足新的水使用用途、回應不斷變化的水自然環境和適應現有用水權利的變化等。簡言之，當自然環境和社會環境出現新的變化時，水資源的既有分配模式需要調整，不然會損害公共利益。但是，水資源分配模式變化頻率不能太過，不然會損害用水者的期待利益。所以，保護水資源之上的公共利益，需要合理平衡公共利益和用水者的私人利益。問題是，如何有效平衡這兩種利益？

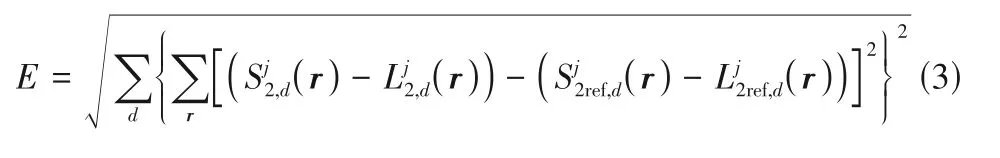
式中，d指模型維度。對于二維圖像，d包含4個維度，即沿x軸和y軸，以及兩個主對角線方向dxy和dyx；對于三維圖像，d包含9 個維度，除了二維的4個方向，還有沿z軸，以及dxz、dzx、dyz和dzy方向。

2.3.3 基于DPN 值的像素交換 模擬退火算法的最重要的過程是在保持多孔電極孔隙率?不變的前提下，通過一定規則產生新結構。將孔隙相和骨架相的像素進行位置交換，等效于產生新結構的過程。

利用傳統的隨機像素交換方法產生新結構時，圖像中所有像素的交換概率相同，這種方法容易破壞已經重構好的局部結構，從而增加了尋找最優結構的時間。同時，圖像中孤立的像素點可以被視為噪點，使用傳統方法也難以去除。本文引入DPN(different phase neighbors)[43]的概念來改進傳統的隨機像素交換方法。像素的DPN 值指在該像素的鄰域內與該像素不同相的像素個數。像素的DPN 值反映了該像素在圖像中的孤立程度，DPN = 0 表明該像素鄰域內所有的像素都與其同相。對于二維圖像，選取8 鄰域；對于三維圖像序列，選取26 鄰域。圖5 列舉了二維圖像中幾種不同的3 × 3 大小的結構，并指出了中心像素的DPN值。

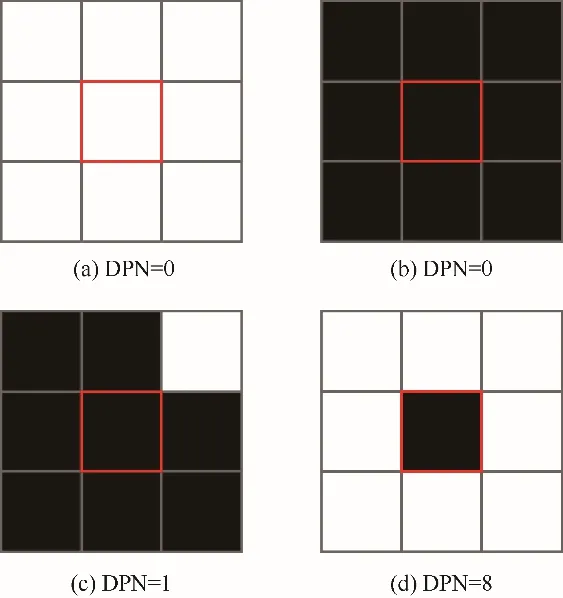
圖5 中心像素在不同結構中的DPN值Fig.5 DPN values of center pixel in different structures

2.3.4 動態退火系數 退火過程就是體系溫度下降的過程。溫度越低，體系跳出當前解的概率就越低。溫度降低太快，容易陷入局部最優；溫度降低太慢，算法運行效率太低。因此，為了平衡精度和速度，需要選取合適的退火方法。常用的退火方法為Tk=λTk-1，其中，k為迭代的次數，λ為退火系數。傳統模擬退火算法的退火系數是常數，無法考慮系統在不同重構階段中能量函數的變化，容易陷入非最優結構或者增加尋優時間。本文采用基于動態退火系數的退火過程，考慮模擬退火過程中系統能量的變化情況，退火系數的計算方法[44]為

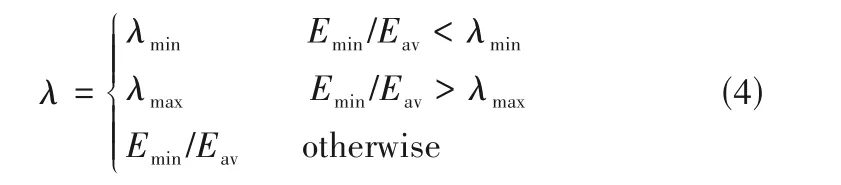
式中，λmin和λmax分別是退火系數的最小值和最大值，用于對退火系數限幅；Emin和Eav是迭代過程中能量函數的最小值和平均值。

2.3.5 參數設置、點云實體化和運行環境 根據前文模擬退火算法的退出條件，設置具體參數如表1所示。

表1 模擬退火算法退出迭代的參數設置Table 1 Parameter setting of simulated annealing algorithm to exit the iteration

通過模擬退火算法產生的點云無法通過有限元方法模擬其內的離子傳遞和電極導熱過程，需要被實體化為由面構成的三維結構。本文采用Blender 自帶的API(application program interface)，將點云實體化為由小立方組成的多孔電極，最后提取表面結構。圖3(c)、(d)分別展示了200 × 200 × 200的多孔電極的骨架相和孔隙相，其中一個小立方體的邊長為8.2 nm。

本文的計算平臺為4 x Intel(R) Xeon(R)Platinum 9242 CPU at 2.30 GHz 和384G 內存的服務器，模擬退火算法和實體化算法通過Python 3.8 編程實現。

2.4 多孔電極的結構參數

孔隙率φ是保證模擬退火算法隨機構造的多孔電極結構符合實際的前提之一。φ的計算方法是孔隙相的立方體數量Np與多孔結構所有立方體數量Nt的比值，即φ=Np/Nt。因為本文構建的多孔結構為實際結構的一小部分，所以構建的多孔結構的六個方向的面為截面而非表面。因此，本文比表面積SV的計算方法為除去截面面積的骨架相表面積與骨架相的體積之比。

首先，通過收集前期地質勘查資料，可以統計出礦區內已知礦體的資源量，計算出各個已知礦體的秩次和齊波夫預測秩，然后，計算齊波夫常數，即求出礦區內潛在的最大礦體的資源量，最后，計算出礦區的總資源量（Q），即Q=F1+F2+……Fn，用資源總量減已知資源量就可以知道礦區內潛在資源量。

多孔電極是分形物質，它的孔隙結構復雜度與其孔隙分形維數等特征參數密切相關。目前常用的計算多孔結構分形維數的方法有盒計數法[45]、豪斯道夫方法[46]和隨機游走法[47]。盒計數法由于其精度更高、運算速度更快而被廣泛用于計算分形維數。對于多孔電極的孔隙體積Vp，有冪律關系Vp(ε) ∝εd，其中，Vp(ε)是在對應長度尺度ε下測得的孔隙體積，d為多孔介質孔隙相的分形維數。對于三維多孔電極,用尺度為ε的立方體測量孔隙體積，則孔隙分形維數計算方法為d= lnNp( )ε/lnε，其中，Np(ε)為在長度尺度ε下識別出孔隙的立方體數量。

模擬退火算法是一種通用的概率優化算法，起源于金屬的退火過程，用于在一個很大的搜尋空間中尋找出最優解，可以求解復雜的非線性優化問題。模擬退火算法其實是一種貪心算法，每次都選擇一個當前最優解，因此只能搜索到局部的最優值。但是它的搜索過程引入了隨機因素。模擬退火算法以一定的概率來接受一個比當前解要差的解，因此有可能會跳出局部的最優解，達到全局的最優解。

所有的結構參數均采用Python 3.8 編程計算。表2 展示了尺寸分別為50 × 50 × 50、100 × 100 ×100和200 × 200 × 200個立方體的多孔電極的結構參數。結果表明多孔電極的尺寸對結構參數影響不大，驗證了重構的多孔電極結構是穩定且有效的。

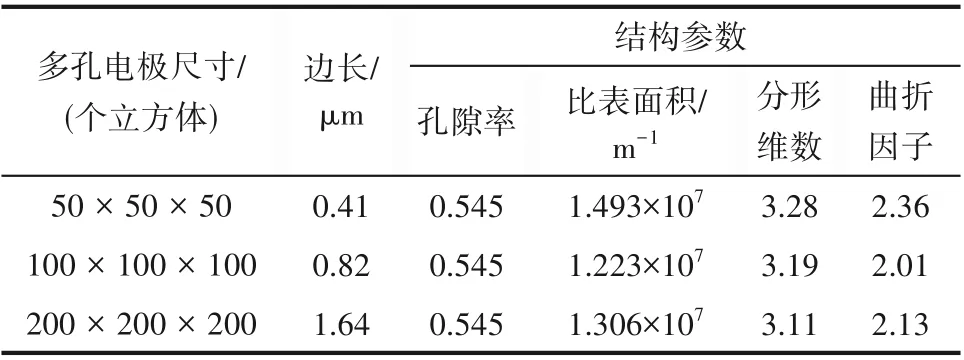
表2 通過模擬退火算法重構的多孔電極的結構參數Table 2 Structural parameters of porous electrode reconstructed by simulated annealing algorithm

3 三維多孔電極中的傳質與傳熱原理

為了研究多孔電極中的傳質和傳熱現象，參考實際超級電容器的工作原理[8]，構建了如圖6所示的兩個模型。受限于計算機的計算資源，離子傳遞模型采用兩個100 × 100 × 100 大小的立方體多孔電極(邊長約為0.82 μm)的孔隙相與200 × 100 × 100大小的長方體體相相接。值得注意的是，兩個孔隙相互為鏡像關系，即右邊的多孔電極是左邊多孔電極經過x、y、z三個方向的鏡像處理后生成的。而電極導熱模型采用100 × 100 × 100 個格子大小的立方體多孔電極的骨架相。

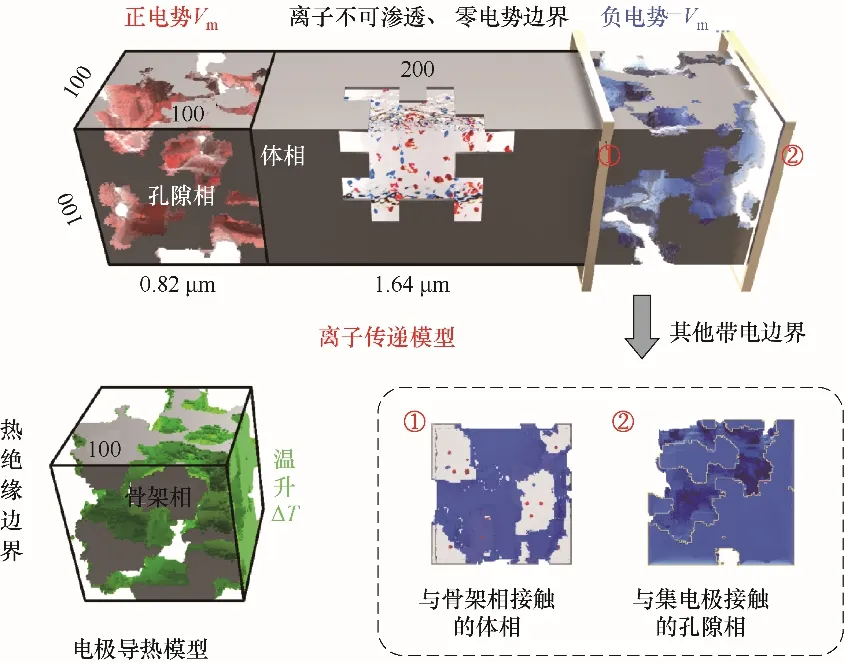
圖6 真實多孔電極中的離子傳遞和電極導熱模型Fig.6 The model of ion transfer and electrode heat conduction in real porous electrodes

3.1 充電過程

剛開始時整個體系的離子密度分布是均勻的，電勢為零。當左右兩個多孔電極施加相反的電勢后，體相和孔隙相中的陰陽離子受到電場力的作用，分別朝著相反的方向定向移動到多孔電極表面，從而形成電流并最終形成雙電層(electrical double layer,EDL)儲存能量。雙電層的厚度通過德拜長度來表示。

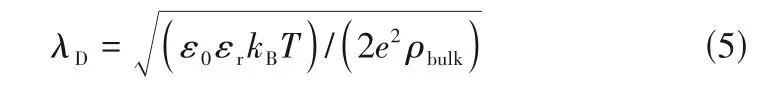
本流域屬亞熱帶氣候，高溫濕潤多雨，具有明顯的干濕季節。東江流域多年平均降水量在1 500 mm～2 400 mm之間，其中4月—9月占全年降雨的80%以上。東江洪水具有水情復雜、洪水遭遇種類繁多等特點。由鋒面雨造成的洪水峰型較肥碩，漲水緩慢。由臺風雨造成的洪水峰型尖瘦，漲落變化快，一次洪水過程一般為6 d～8 d。東江三角洲的潮汐屬不規則半日潮，日潮不等現象顯著。由于受徑流和臺風的影響，年最高潮位一般出現于汛期。

本文考慮到生成的雙電層不會發生重疊以及求解的復雜度兩個因素，于是采用Poisson-Nernst-Planck(PNP)方程來描述上述復雜孔隙結構中的離子充電動力學。電勢?(V)和離子的數密度ρ(m-3)是PNP方程要求解的變量，其控制方程形式為：

設由兩個多孔電極的孔隙相和體相組成的離子運動空間為Ω。剛開始時整個空間的離子數密度ρ是均勻分布的，電勢?為零，即

本試驗采用隨機排列，不設重復。①九麥2號4.6畝；②中麥895 1.55畝；③小偃22（CK）1.55畝；④秦農578 0.72畝；⑤西農223 1.65畝；⑥陜農33 1.8畝；⑦武農6號1.44畝；⑧凳峰168 1.2畝；合計占地14.5畝。（田間排列設置見附表1）。

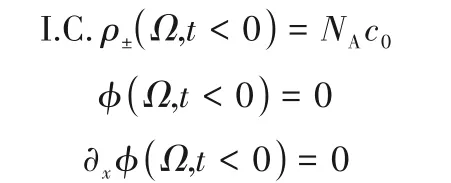
式中，NA是阿伏伽德羅常數。

因為多孔炭電極是良好的導體，所以可以假設整個多孔炭電極是一個等勢體，即多孔電極和電解液的界面處的電勢相等。圖6中紅色和藍色區域代表電解液和多孔電極的界面以及電解液和集電極的界面，分別帶正電勢Vm和負電勢-Vm，其中Vm=kBT/e為熱電勢。由于重構出的多孔電極并不是周期性結構，不能采用周期性邊界條件，所以本文采用不可滲透且電勢為零的邊界條件，即灰色區域。因此。設帶正電的邊界為S+，帶負電的邊界為S-，其他邊界為S0，則

本文基于COMSOL Multiphysics 5.4 軟件，采用有限元法求解上述含有復雜邊界條件的PNP 方程，從而得到離子在多孔電極中的遷移行為。計算平臺為4 x Intel(R) Xeon(R) Platinum 9242 CPU at 2.30 GHz和384G內存的服務器。

3.2 導熱過程

在實際的充放電過程中，由于電流的生成和離子的重排等因素[15]，整個體系會產生熱量。體系溫度主要受到熱生成、電解液內部的熱傳導和熱對流，以及多孔電極內的熱傳導影響。而溫度又會影響離子的輸運參數和電極的導電性能，從而影響整個充電過程。充電、產熱和傳熱三種現象相互耦合，極大地增加了計算量。此外，本文研究體系的電極導熱的弛豫時間遠小于充電的弛豫時間(或產熱的弛豫時間)，且模擬時間較短，可以將充電現象和電極導熱現象解耦，從而分開研究。因此，為了簡化電極導熱模型，只考慮電極中的熱傳導。本文采用傅里葉定律描述熱傳導過程。

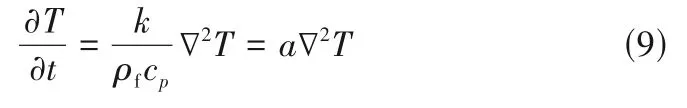
式中，k是熱導率，W·m-1·K-1;ρf是骨架質量密度，kg·m-3;cp是骨架相的比定壓熱容，J·kg-1·K-1;a是熱擴散系數，m2·s-1。

設骨架相空間為γ，骨架相的初始溫度為T0，即

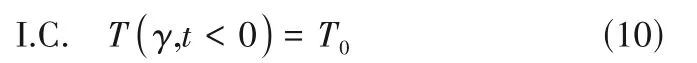
熱量通過電解液和電極的界面從電解液傳入電極中，設電解液和電極的界面為ΛT，并假設ΛT上產生不隨時間和位置發生變化的溫升ΔT0。同2.1節，因為不能設置周期性邊界條件，所以假設其他面Λ0是熱絕緣邊界。因此邊界條件為

E農1S是湖北省農業科學院糧食作物研究所以廣占 63－4S［1］為受體、以抗稻瘟病品種 GD－7［2］為供體，通過雜交、回交和自交，結合分子標記輔助選擇技術選育的攜帶抗稻瘟病基因Pi1和Pi2的兩系不育系。2016年通過湖北省農作物品種審定委員會審定，品種審定編號為鄂審稻2016028。以E農1S為母本配制的雜交組合目前已有E兩優476［3］、E兩優186［4］和E兩優222通過了品種審定。

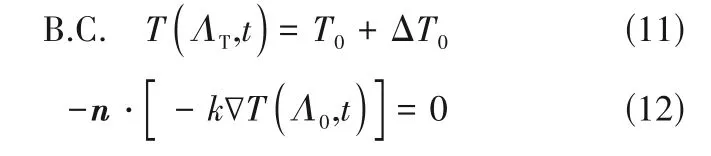
式中，n是法線方向的單位向量。

Kunanusont 等[24]只測量了多孔炭電極的電導率。因此，根據文獻[51]，設置多孔炭電極的k=0.81 W ?m-1?K-1。 假設ρf= 1100 kg ?m-3，cp=1100 J ?kg-1?K-1，則a= 6.69 × 10-7m2?s-1，τa=1.01 × 10-6s， ΔT0= 0.1 K。 模 擬 時 間 為(10-3～10-1)τa，其中τa=H2/a為表征厚度為H的平板電極在表面加溫后整個電極內部的溫度達到均一時的時間[51]。

電極導熱過程同樣基于COMSOL Multiphysics 5.4 軟件，采用有限元法求解。計算平臺為4 x Intel(R) Xeon(R) Platinum 9242 CPU at 2.30 GHz 和384G內存的服務器。

臨床研究表明,產后出血是臨床常見,也是最嚴重的分娩并發癥之一。若產婦在孕中出血過多,會因出血過多而死亡,不僅影響到產婦本人的身體健康,甚至會威脅到生命安全。初期臨產婦在心情上也會表現出焦慮、沮喪、心情壓抑等,所以助產士在生產過程全程陪同并且運用科學合理的護理方式十分重要。產后出血是表示在分娩后24h內大量出血(出血量超過500ml),出血原因包括宮縮乏力、產道損傷、胎盤因素、凝血功能差等等。研究顯示,子宮收縮無力是導致產后出血的主要原因,若產房助產士能在孕前密切關注產婦動態,并做好一系列急救措施準備,方能將大出血概率降到最低。

4 三維多孔電極中的傳質與傳熱原理

本節首先驗證了改進后的模擬退火算法的高效性，然后模擬了如圖6 所示的多孔電極模型中的離子傳遞和電極導熱現象。

4.1 改進的模擬退火算法結果

為了驗證改進后的模擬退火算法重構的準確性，圖7 展示了重構結構w的能量函數E(w)隨迭代次數的變化曲線。結果表明相較于隨機的像素交換策略和靜態的退火系數的經典模擬退火算法，采用DPN 值的像素交換策略和采用動態的退火系數的改進模擬退火算法在相同的迭代次數下的重構精度更高(即E(w)更小)。但由于每次迭代需要計算每個像素點的DPN 值，所以花費的總時間也更長。但是，由于改進的模擬退火算法在每次迭代時E(w)下降的值更大(即斜率更大)，所以單位時間內E(w)的減小量可能也更大（即重構效率更高）。

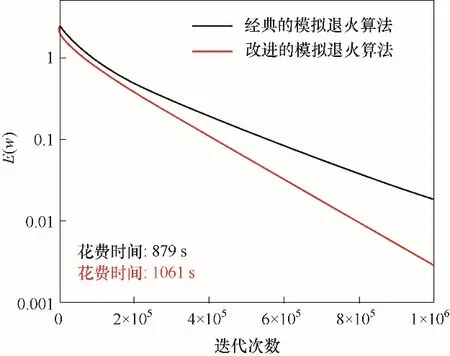
圖7 重構結構的能量函數隨迭代次數的變化Fig.7 The energy function of the reconstructed structure varies with the number of iterations

4.2 離子傳遞

陰陽離子在電勢的驅動下，分別朝著正極和負極移動。10-1τRC時整個超級電容器的電勢分布?/Vm如圖8(a)所示，正極部分的孔隙相為高電勢，負極部分的孔隙相為低電勢，體相的電勢則整體線性變化。圖8(b)、(c)分別展示了正極部分的孔隙相與體相的截面處(x= -L)以及此截面前一個小立方體邊長距離的截面處(x= -L+ 0.01H)的?/Vm。如邊界條件設置一樣，多孔電極的骨架相和體相的接觸面的電勢?始終為Vm，即圖8(b)中紅色區域?/Vm= 1。此外，電勢在yz平面并不是均勻的，骨架相附近的電勢較高，且電勢隨著x的變化而存在較大的變化。

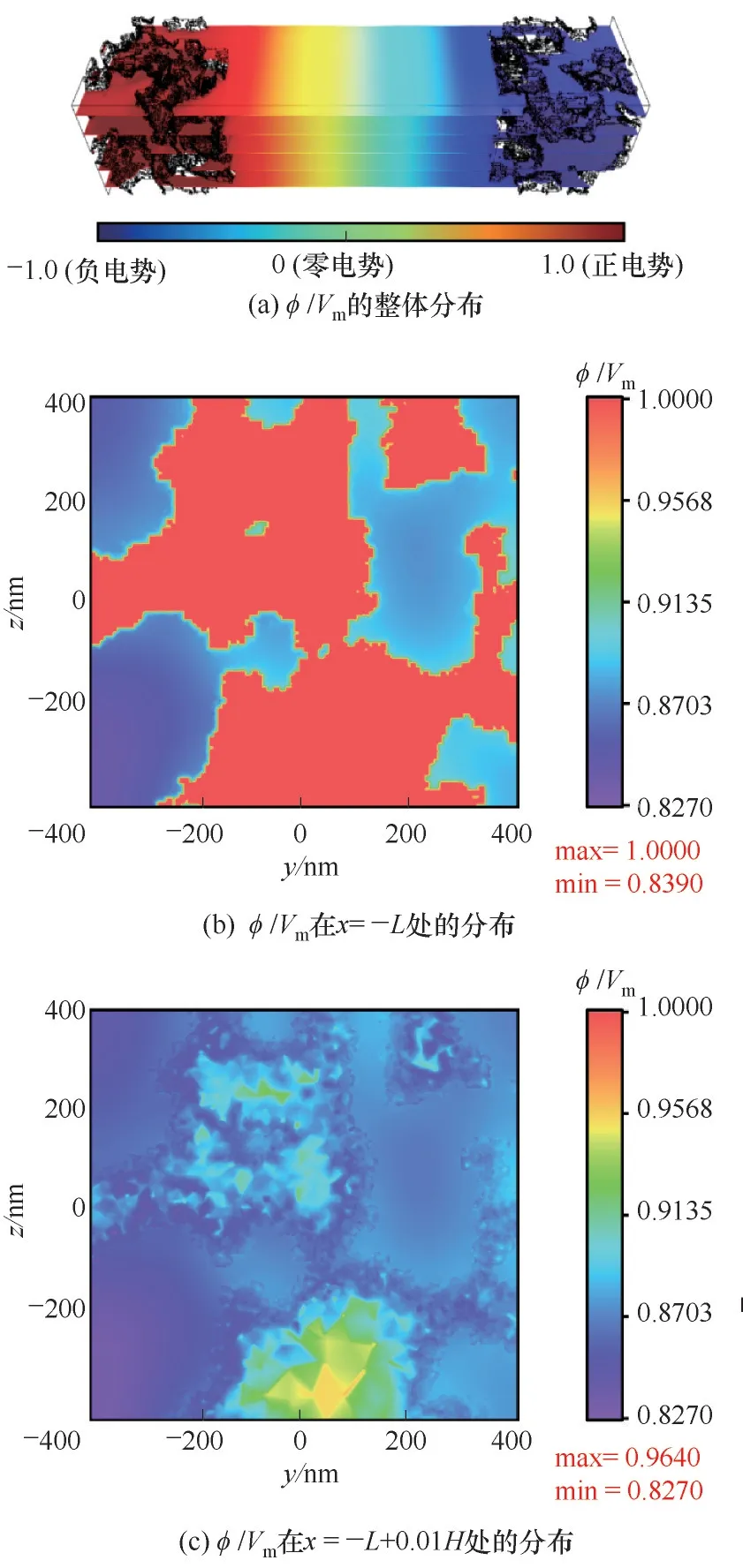
圖8 10-1τRC時不同位置的電勢分布?/VmFig.8 The potential distribution ?/Vm at different position at 10-1τRC

圖9展示了陰陽離子濃度分布的歸一化平均值(c++c-)/(2c0)。因為模擬時間只有10-1τRC，所以陰陽離子主要朝與體相接觸的骨架相截面遷移，較少地往孔中遷移。此外，結果還表明，陰陽離子更傾向于從截面的邊緣往中心遷移，如圖9(b)所示，邊緣的(c++c-)/(2c0)大于中心的。而遷移的離子來自于體相對應的位置，如圖9(c)所示，邊緣的(c++c-)/(2c0)小于中心的。

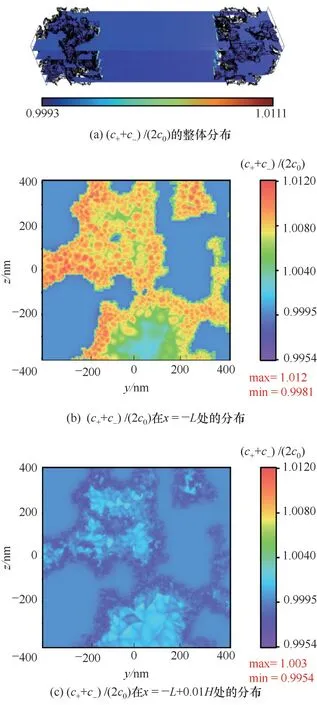
圖9 10-1τRC時不同位置的濃度分布(c+ + c-)/(2c0)Fig.9 The concentration distribution(c+ + c-)/(2c0)at different position at 10-1τRC

4.3 電極導熱

圖10 為多孔電極中的歸一化溫度分布[(T-T0)]/ΔT0隨時間變化的等值面圖，包括在10-3τa、10-2τa和10-1τa時刻下。圖中黃色區域，即[(T-T0)]/ΔT0= 0，代表低溫; 白色區域，即(T-T0)/ΔT0= 1，代表高溫。當(T-T0)/ΔT0= 0 時，表明熱量還沒傳導到這個位置；當(T-T0)/ΔT0= 1時，說明此時溫度已經上升到能達到的最高溫度T0+ ΔT0。結果表明：在10-1τa時，多孔電極的整個骨架相幾乎都是白色，表明從導熱邊界傳遞給骨架相的熱量已經完全傳遞到各個角落，骨架相的溫度已經均勻分布。此時的時間10-1τa遠小于平板電極的溫度弛豫時間τa，原因是熱量不僅僅是從骨架相與體相接觸的界面傳導入骨架相的，還包括孔道內部的壁面，從而減小了實際的導熱距離，最終使在多孔電極中的熱弛豫時間遠小于平板的弛豫時間τa。

圖10 不同時刻下的溫度分布(T - T0)/ΔT0的等值面圖Fig.10 Theisosurface diagram of temperature distribution(T - T0)/ΔT0 at different time

5 結 論

（1）一種改進的模擬退火算法重構出的多孔電極結構是穩定且有效的。

E,Eth,Emin,Eav——分別為能量函數、退出迭代的能量閾值、迭代過程中能量函數的最小值和平均值

（3）當充電時間為10-1τRC時，陰陽離子主要吸附在多孔電極骨架相與體相的接觸面上，且陰陽離子從截面邊緣往中心遷移。

（4）由于電解液深入多孔電極內部，導致實際的導熱距離遠小于多孔電極厚度，于是多孔電極中的熱弛豫時間遠小于平板的弛豫時間τa。

D——離子擴散系數，m2·s-1

符 號 說 明

a——熱擴散系數，m2·s-1

cp——骨架相的比定壓熱容，J·kg-1·K-1

c+,c-,c0——分別為陽離子、陰離子的濃度和初始濃度，mol·m-3

2011年春節前夕，吳霞還沒有回來。江帆找人破譯了吳霞的QQ密碼。他瀏覽妻子的聊天記錄發現，從2009年國慶前后，妻子認識了一個昵稱“蠟筆老新”的網友。后來，兩人頻頻相約參加一些聚眾的“轟趴”，正式成為朋友。吳霞自小就練習小提琴，對樂器有著由衷的熱愛，“蠟筆老新”正好精于此道，兩人由此打開了話題，在網上聊得不亦樂乎，“蠟筆老新”的幽默詼諧，經常逗得吳霞哈哈大笑。在“蠟筆老新”的QQ資料欄上，公然寫著“某某樂器廠總經理李輝”。江帆一看，怒從中來，這個李輝，不就是自己的高中同學么？

采用更加真實的物理模型和求解方法用于真實多孔電極中的離子傳遞和電極導熱現象是未來的重點研究方向。PNP方程并沒有考慮離子的體積排阻效應，而是假定所有離子是點粒子。離子體積在多孔電極內，尤其是高濃度和高電壓時，會極大地影響離子傳遞現象。為此，Kilic 等[52]推導出包含體積排阻效應的MPNP 方程。進一步地，為了更全面地彌補連續介質模型在介觀尺度下對微觀信息的缺失，還可以采用多尺度多物理場經典密度泛函理論代替MPNP 方程[7]。目前通過有限元方法求解含有復雜邊界條件的偏微分方程組需要消耗大量計算資源，難以深入研究多孔電極結構對熱-質傳遞現象的影響。因此，亟需快速準確求解含有復雜邊界條件的偏微分方程組的方法，比如格子Boltzmann 方法[53](lattice Boltzmann method，LBM)和神經網絡(neural network，NN)[54]。

d——分形維數

通過以上史料的對比介紹不難發現，《冊府元龜》《新唐書》由于借鑒了《舊唐書》和其他資料，因而關于張均流放合浦郡的說法一致；而對于張垍之死的說法，《新唐書》與《舊唐書》雖有歧異，但以《舊唐書》更為準確，似無可疑。宋敏求的《唐大詔令集》為本取材于唐代國史、實錄等資料的《舊唐書》對關于二張之死的記載又增添了強有力的證據。

（2）多孔電極內的電勢分布不均勻，體相中的電勢沿x方向整體線性變化。

Np——孔隙相立方體的數量

e——基本電荷，C

H——電極厚度，m

J——離子通量，m3·s-1

k——熱導率，W·m-1·K-1

kB——Boltzmann常數，J·K-1

L——體相半長，m

l——孔隙相的傳輸路徑總長度，m

其次，課程設置不盡合理。當前高校旅游專業的培養模式和課程體系，不能夠完全適應市場的需求，專業課程設置脫離實際，普遍重理論輕實踐，缺乏實際操作技能和行業管理經驗，各院校于業界之間缺乏足夠的交流，比如，高檔酒店需要英語流利、聽說能力強的就業者，但現實中很大一部分學生達不到此標準。還有，教學設施設備條件不足等情況都或多或少的存在，與需求錯位現象非常嚴重，這就很難培養出來具有創新意識、創業能力的特色旅游人才。

NA——阿伏伽德羅常數

Ncon,Niter——分別為連續拒絕隨機產生的新結構的次數的上限值和模擬退火算法可以迭代的最大次數

ΔE,ΔEth——分別為能量增量和退出迭代的能量增量閾值

Nt——多孔電極所有立方體的數量

鍋爐汽包水位自動調節的任務是使給水量與鍋爐的蒸發量相平衡，并維持汽包中的水位在工藝允許的范圍內。水位過高，會影響汽包內汽水分離效果，使汽包出口的飽和蒸汽帶水增多，造成不良后果；水位過低則造成水的急速蒸發，汽水自然循環破壞，鍋爐壁容易被燒壞，嚴重時會造成爆炸事故。

n——法線方向的單位向量

q——電荷數密度，m-3

康寧大草原休閑旅游帶規劃范圍為壩上大灘鎮為起點，延張承高速，到魚兒山向東，涵蓋了豐寧的西部與北部地區。以“京北第一草原”這一核心為依托，綜合壩上草原不同鄉村的文化特征與地形地貌，打造以草原為中心，以草原文化為依托，茶鹽古道為基礎的休閑旅游帶，形成集草原風情、影視攝影、歷史典故、民族文化、低碳環保、工業科普、休閑運動等為一身的綜合休閑旅游帶，帶動豐寧西北地區鄉村旅游發展。

S+,S-,S0——分別為帶正電、帶負電和不帶電的邊界

T,T0——分別為局部溫度和體系初始溫度，K

Tk-1,Tk——分別為第k-1、k次迭代時的溫度，K

ΔT0——溫升，K

t——時間，s

V——多孔介質某個相所占的區域

Vm——熱電勢，V

Vp——孔隙相體積，m3

w0,w,w′——分別為參考模型的二維結構、模擬退火算法的初始三維結構和下一步生成的三維結構

z——離子的價態

γ——骨架相空間

ε——長度尺度，m

εr——相對介電常數，F·m-1

ε0——真空介電常數，F·m-1

ΛT,Λ0——分別為溫升邊界和絕熱邊界

λ,λmin,λmax——分別為退火系數、退火系數的最小值和最大值

λD——德拜長度，m

ρbulk——體相離子數密度，m-3

ρf——骨架質量密度，kg·m-3

τ——曲折因子

τa——單板電極中熱傳導的弛豫時間，s

τRC——單板電極中離子傳遞的弛豫時間，s

?——電勢，V

φj,φ——分別為多孔介質第j相的濃度和多孔介質的孔隙率

Ω——離子運動空間

上角標

j——多孔介質某個相的序號

下角標

av——平均值

con——新結構連續被拒絕

f——骨架相

iter——迭代

k——迭代次數

min——最小值

r——相對

r——圖像中任意一點的位置

th——閾值

-——帶負電

+——帶正電

±——陰陽離子