風電機組偏航誤差產生機理及調整策略研究

徐 昆

(北方工業大學，北京 100144)

0 引言

風電機組采用的偏航系統是根據風向標測得的風向信息執行偏航動作，但其在偏航過程中往往存在對風偏差，這不僅會降低風電機組的風能捕獲能力，還會導致風輪受力不均、風電機組運行荷載增大[1]，加速偏航系統機械疲勞，進而引發偏航系統機械部件故障。文獻[2]通過1997—2005年期間瑞典風電場的風電機組故障原因調查結果發現，偏航系統故障率占風電機組總故障率的7%左右。隨著風電裝機容量日益增長，因偏航系統誤差(下文簡稱為“偏航誤差”)導致的偏航系統故障引發的風電機組停機事故已嚴重影響風電場經濟效益，減少偏航誤差得到了風電場管理者的普遍重視。依據產生機理不同，偏航誤差分為偏航靜態誤差和偏航控制策略誤差。因此分析偏航誤差產生機理、采取相應調整策略減少偏航誤差對優化和提高偏航系統性能、保障風電機組安全穩定運行意義重大。基于此，本文對偏航靜態誤差和偏航控制策略誤差的產生機理進行了介紹，并針對這2種誤差分別提出了各自的調整策略。

1 偏航靜態誤差產生機理及調整策略

1.1 偏航靜態誤差產生機理

1.1.1 偏航誤差

風向標測量結果準確無誤時，其零刻線與風輪軸線處于平行狀態，即二者的夾角為0°；當二者的夾角不為0°時，則此夾角就是偏航誤差，其包含偏航靜態誤差和偏航控制策略誤差2種。

1.1.2 偏航靜態誤差及產生機理

初次安裝調試風向標時未對零、風向標測量精度低、風況復雜、尾流影響等因素，都會導致風向標測得的風向與實際風向之間存在一定的角度差，此現象被稱為偏航靜態誤差，其示意圖如圖1所示。圖中：φ為實際風向與風輪軸線夾角，即偏航誤差角[3]，(°)；α為風向標監測風向與風輪軸線夾角，(°)；θ為偏航靜態誤差角。三者之間的關系如式(1)所示。

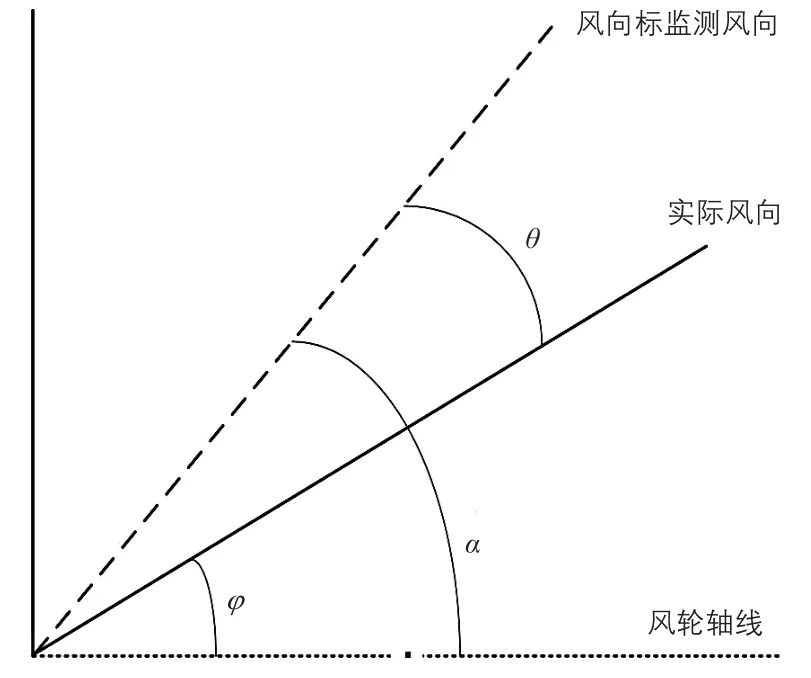
圖1 偏航靜態誤差示意圖Fig. 1 Schematic diagram of yaw static error

偏航靜態誤差的本質就是風向標監測得到的風向偏離實際風向的角度。

1.2 偏航靜態誤差調整策略

1.2.1 基于激光雷達的調整策略

風電機組的輸出功率P可表示為：

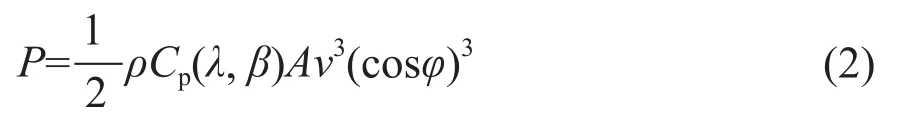
式中：ρ為空氣密度，kg/m3；Cp為風能利用系數；λ為葉尖速比；β為槳距角，(° )；A為風輪掃掠面積，m2；ν為風速，m/s。

由式(2)可知：實際風向與風輪軸線夾角的絕對值越大，風電機組的輸出功率越小，說明風電機組的輸出功率損失變大，同時也意味著風電機組的性能變差。當實際風向與風輪軸線夾角的絕對值為10°時，風電機組的輸出功率損失為4.48%；當實際風向與風輪軸線夾角的絕對值為15°時，風電機組的輸出功率損失為9.87%[4]。

設風能利用系數為定值，則風電機組的輸出功率變化量ΔP可表示為：

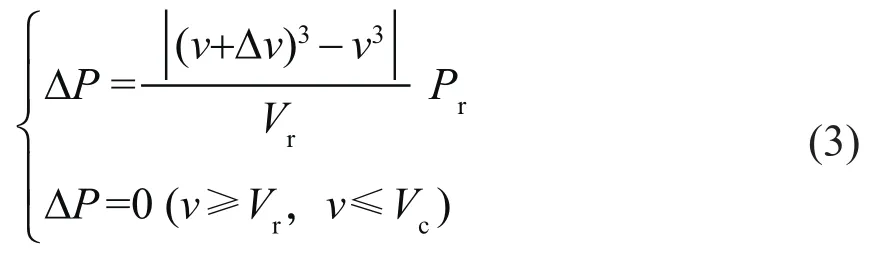
式中：Δv為風速變化量，m/s；Vr為額定風速，m/s；Vc為切入風速，m/s。

在額定風速時，風電機組會達到額定輸出功率，并保持恒功率運行。在切入風速與額定風速區間內，風電機組的輸出功率與風速之間的關系如圖2所示。

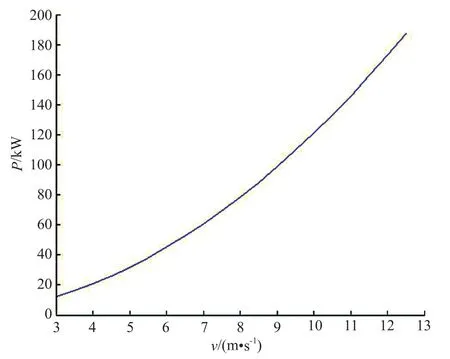
圖2 風電機組輸出功率與風速之間的關系Fig. 2 Relationship between wind turbine output power and wind speed

由圖2可知：在3.0～6.5 m/s低風速區間，隨著風速增加，風電機組輸出功率的變化平緩；在6.5～9.5 m/s中風速區間及9.5～12.5 m/s高風速區間，隨著風速增加，風電機組輸出功率的變化越來越大。

進一步分析可以發現，計及偏航靜態誤差時的風電機組輸出功率變化量ΔP′可表示為：

風電機組安裝調試、投入運行后，不同機位風電機組的偏航控制系統對風向變化的響應性能可能會存在較大差異。再加上機位分布范圍廣、各機位地形不一，很難通過建模仿真來全面、精確地描述風電機組偏航靜態誤差。因此對位于各種地形機位上的風電機組進行偏航靜態誤差實測，可以獲得較為精確的偏航靜態誤差數據，對于評估、調整偏航靜態誤差具有重要的現實意義。基于此，提出了基于激光雷達的偏航靜態誤差實測分析方法。

激光雷達測風儀是糾正偏航靜態誤差所采用的一種設備，其安裝位置如圖3所示。

圖3 激光雷達測風儀的安裝位置Fig. 3 Installation location of lidar wind meter

為提高激光雷達測風儀測量準確性，設計如下數據采集方案：1)從風電機組的風輪處開始測量，水平方向每隔1個風輪半徑設置1個測試點，共設置5個測試點；2)從切入風速開始每隔0.5 m/s風速采集3組數據，直到達到額定風速為止；3)每個測試點需采集風速和風向數據，采集完成后將數據代入式(5)～式(6)。

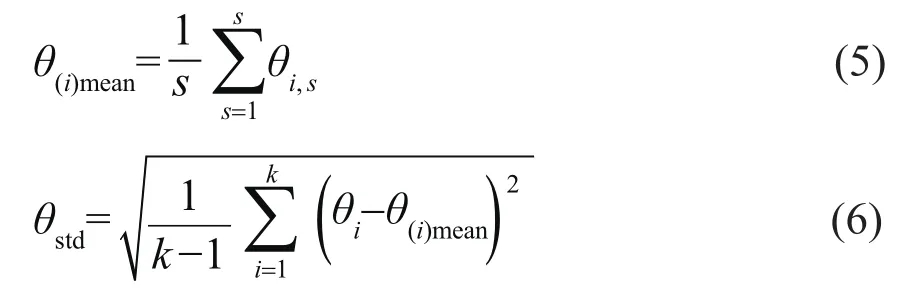
式中：θi為第i個測試點的偏航靜態誤差最大值；θi,s為第i個測試點第s次的偏航靜態誤差；k為總的測試點數量；θ(i)mean為第i個測試點的偏航靜態誤差平均值；θstd為偏航靜態誤差的標準差。

通過上述初步計算后，再對數據進行有效性篩選，以進一步提高計算偏航靜態誤差的精確性。有效數據必須是風電機組保持運行狀態時測量得到的、偏航靜態誤差標準差小于5°的測量數據，偏航靜態誤差的數據應在[-30°, 30°]范圍內。得到有效數據后將其代入式(7)。

式中：θ(i)eff,mean為第i個測試點偏航靜態誤差有效值的平均值。

為驗證激光雷達測風儀所測數據的準確性及所提調整策略的有效性，以從某風電場的133臺風電機組采集的SCADA數據為例，采集時間長度為2018-02-01～2019-05-01及2019-11-01～2020-05-01，數據分辨率為10 min。由于數據量巨大，僅以其中的52#風電機組的數據進行舉例說明。52#風電機組的偏航系統存在偏航靜態誤差，通過分析52#風電機組的SCADA數據，繪制偏航靜態誤差對其輸出功率的影響聚類圖，如圖4所示。由圖4可知：52#風電機組的偏航靜態誤差對輸出功率存在影響。

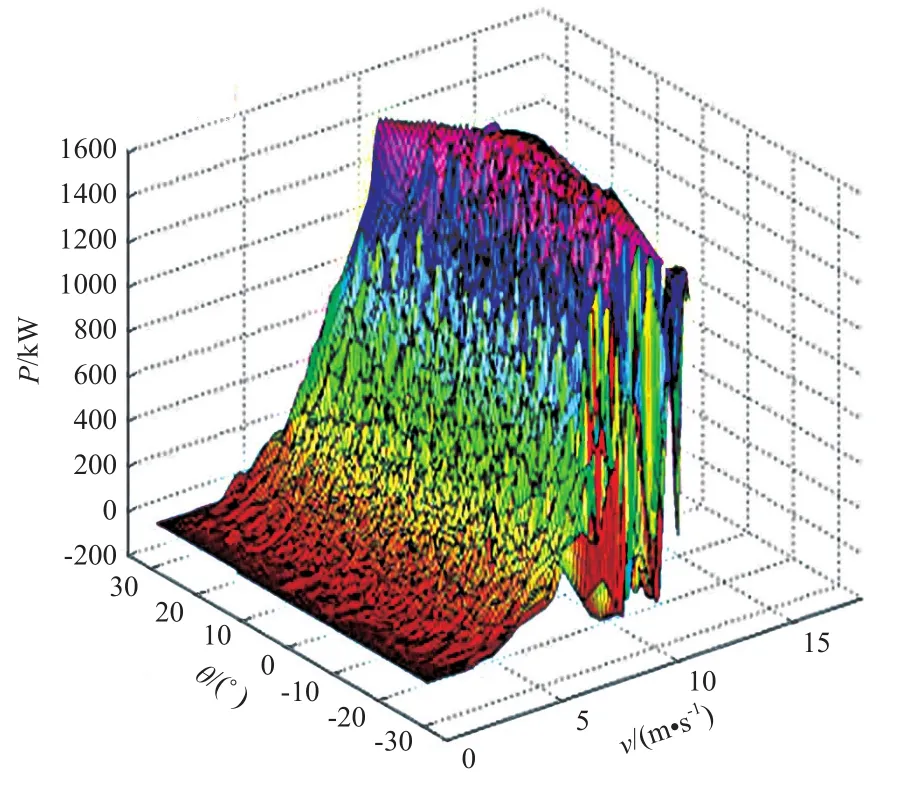
圖4 偏航靜態誤差對風電機組輸出功率的影響Fig. 4 Influence of yaw static error on output power of wind turbine

利用激光雷達測風儀對52#風電機組的風速、風向進行實測，然后實施偏航靜態誤差校正，校正時間為2020-02-01～2020-05-01，并做橫向與縱向發電量對比分析。橫向分析是指將52#風電機組在2019-11-01～2020-02-01與2020-02-01～2020-05-01這2個時間區間的發電量增長率與相鄰未校正的51#、53#風電機組在這2個時間區間的發電量增長率作對比分析；縱向分析是指將52#風電機組進行2020-02-01～2020-05-01與2018-02-01～2019-05-01的發電量對比。橫向分析時將51#、52#、53#風電機組在上述2個時間區間內的平均風速折算為同一基準，結果發現發電量分別增長了0.36%、1.29%、-0.67%。縱向分析時將52#風電機組在上述2個時間區間內的平均風速折算為同一基準后發現，經過偏航靜態誤差校正后，52#風電機組的發電量增長了2.39%。驗證了激光雷達測風儀所測數據的準確性及該調整策略的有效性。

1.2.2 基于最佳葉尖速比風向補償因數修正的調整策略

按以下步驟對數據進行處理：1)剔除風電機組故障停機、非正常運行狀態、葉片槳距角不為0°及運行在額定風速以上時的數據；2)剔除控制因素對輸出功率產生影響的數據。葉尖速比λ是衡量風電機組控制系統性能的重要參數，對輸出功率影響較大[5]。風電機組風能利用系數Cp與葉尖速比之間的關系可表示為：

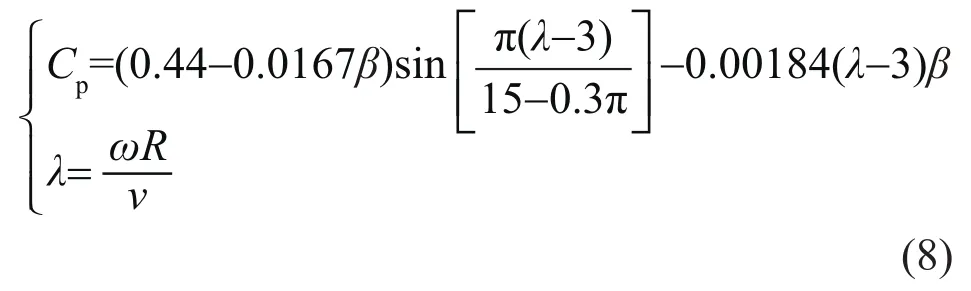
式中：ω為葉輪轉速；R為葉輪半徑。

繪制風電機組風能利用系數隨風速變化趨勢圖，如圖5所示。

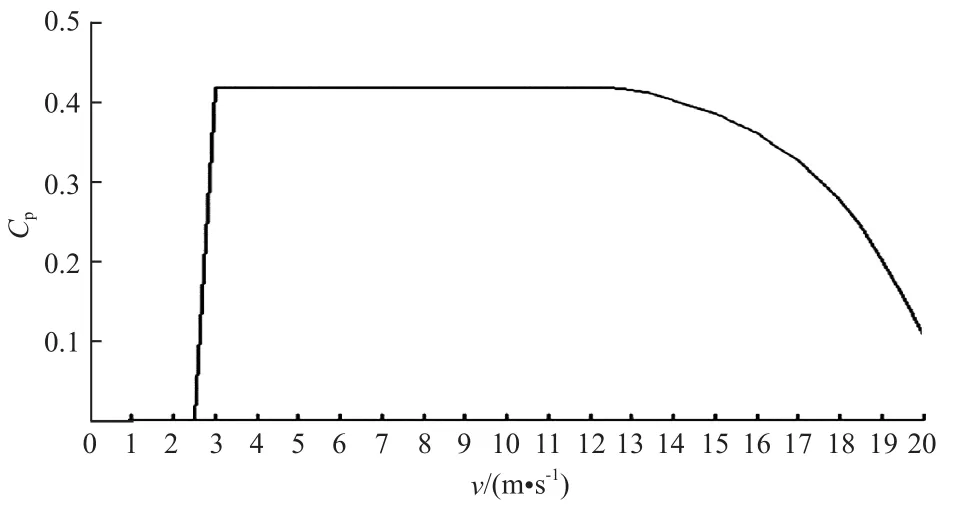
圖5 風電機組風能利用系數隨風速變化趨勢圖Fig. 5 Trend of wind energy utilization coefficient of wind turbine with wind speed

由圖5可知：風能利用系數在切入風速3.0 m/s與額定風速12.5 m/s區間最高，超過額定風速會逐漸下降。再結合式(8)可知：此風速區間內葉尖速比變化小，且風電機組的槳距角為0°，風電機組控制系統對風電機組發電量的干擾程度最低，風能利用系數基本是一條水平直線。因此，該區間內的運行數據可以排除控制系統對輸出功率的影響。

依據式 (8)繪制槳距角為 0°、2°、5°、10°、15°時，風能利用系數與葉尖速比的關系曲線，如圖6所示。

由圖6可知：當槳距角為定值時，存在唯一與之對應的最大風能利用系數Cpmax，此時的葉尖速比為最佳葉尖速比。根據風向標受尾流影響時其測風向偏差θ′，可得到風電機組總偏航靜態誤差θS為：

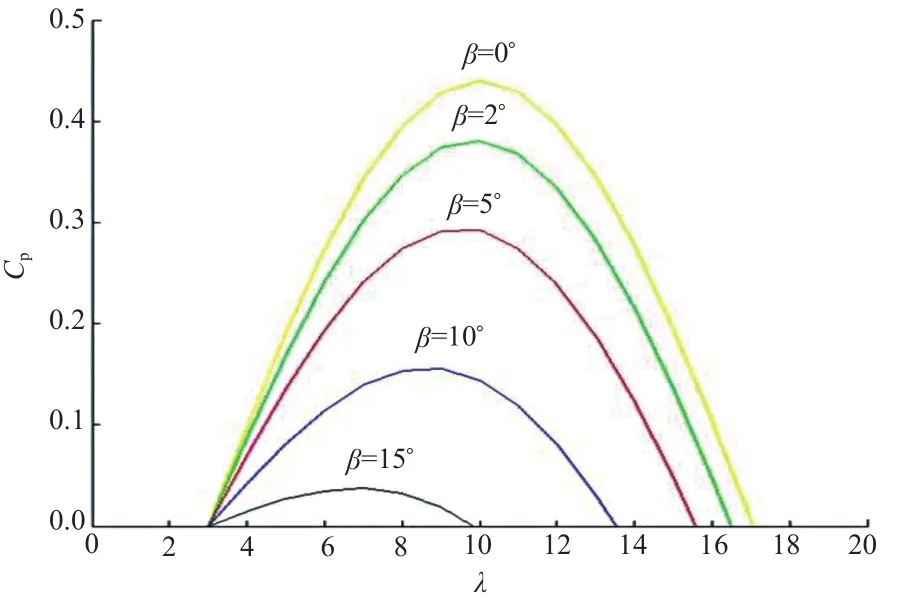
圖6 風能利用系數與葉尖速比的關系曲線圖Fig. 6 relationship between wind energy utilization coefficient and tip speed ratio

為消除偏航靜態誤差產生的影響，需進行風向補償。風向補償角θb可表示為：

式中：kb為風向補償因數；ωG為風電機組的發電機額定轉速，此處取1500 r/min；θaco為風向補償后偏航靜態誤差。

通過激光雷達測風儀實測得到某風電場中4#風電機組的風向為-9.5°，即偏航靜態誤差為9.5°，而4#風電機組的風向補償因數初始值為0.0058，由式(10)可知，ωG=1500 r/min時，風向補償角為8.7°。

為進一步減小偏航靜態誤差，依據式(10)將風向補償因數修正為0.0063。風電機組采用風向補償因數修正值運行一段時間后，重新利用激光雷達測風儀對風電機組進行偏航靜態誤差實測，并進行分析。采用風向補償因數修正值后實測得到的風向柱狀圖及SCADA采集得到的風向柱狀圖分別如圖7、圖8所示。

通過圖7可知：測風儀所測的4#風電機組偏航靜態誤差為-9.5，即偏航靜態誤差沒變。由圖8可知：通過風向補償因數修正使運行狀態下偏航靜態誤差趨向于0°。對比圖7、圖8可知：風向補償因數由0.0058修正為0.0063后，實測數據與修正前相比進一步減小。由此可知，通過多次風向補償因數修正與實測可以最大程度減小乃至消除偏航靜態誤差。這表明了基于最佳葉尖速比的風向補償因數修正的偏航靜態誤差調整策略的有效性。

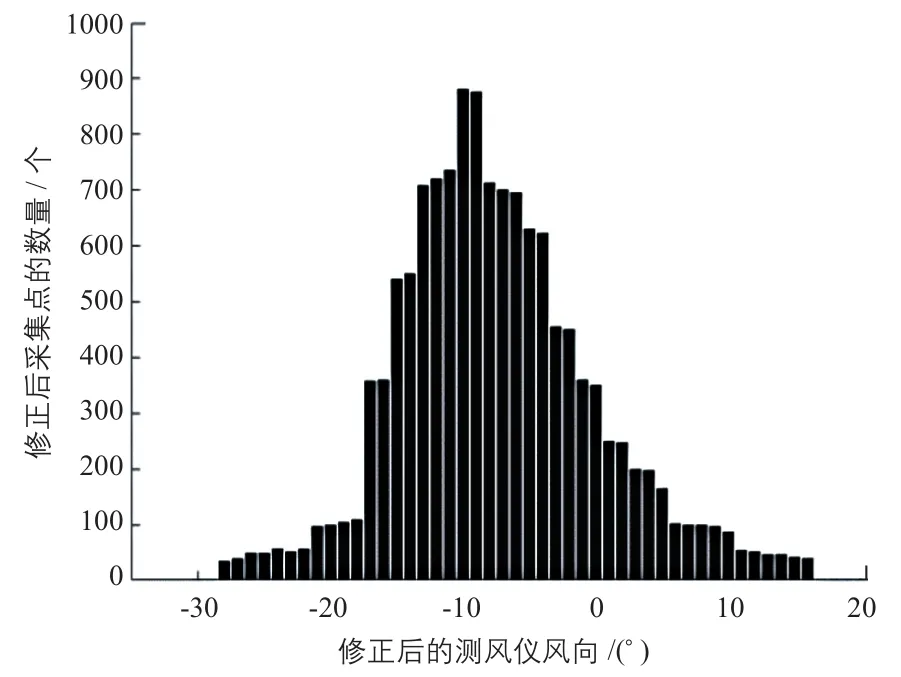
圖7 修正后的測風儀風向柱狀圖Fig. 7 Wind direction histogram of wind meter after correction

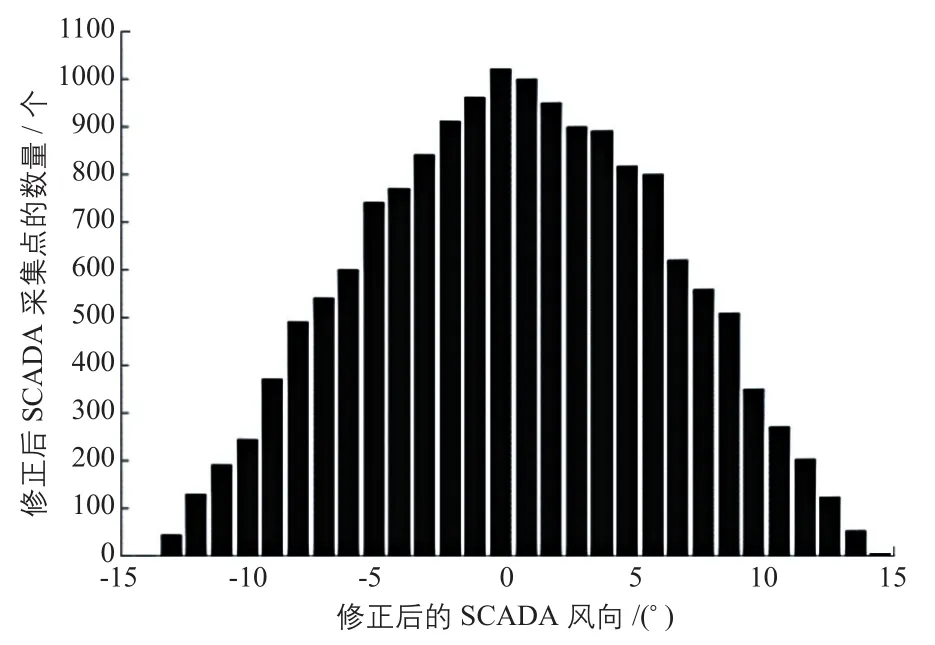
圖8 修正后的SCADA風向柱狀圖Fig. 8 Wind direction histogram of SCADA after correction

2 偏航控制策略誤差產生機理及調整策略

2.1 偏航控制策略誤差產生機理

風向突然改變時偏航系統很難正確跟蹤風向的變化[6]，會出現偏航超前、滯后、對風精度低等現象；風向變化頻繁時無效偏航次數增加，會加快偏航系統機械部件的磨損。

2.2 反向傳播(BP)神經網絡LM算法風向預測優化模型

2.2.1 BP神經網絡模型

神經網絡方法不僅對非線性數據處理具有先天優勢，還可以通過訓練根據之前數據完成對之后數據的預測[7]，而不需要建立一個精確的數學模型[8]。BP神經網絡的結構圖如圖9所示。圖中：xm、yn分別為輸入節點號和輸出節點號；j、h、l分別為輸入層、隱藏層、輸出層。

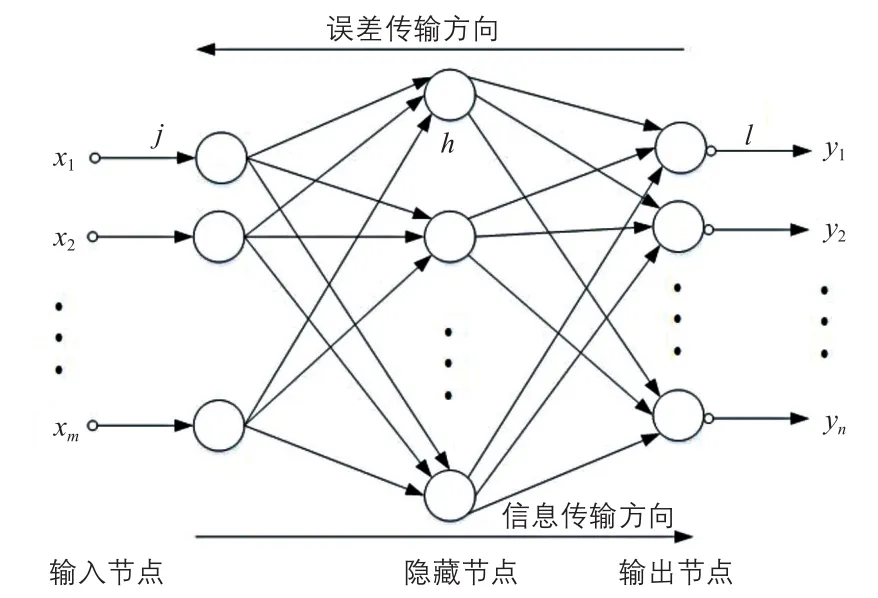
圖9 BP神經網絡結構圖Fig. 9 Structure diagram of BP neural network

從圖9中可以看出：BP 神經網絡是典型的3層網絡結構。隱藏層節點數q經驗計算式為：

式中：m、n分別為輸入、輸出節點數；a為常數，取值范圍為[1,10]。

2.2.2 風向預測優化模型

風向預測優化模型的建立步驟為：首先建立系統辨識網絡模型，神經網絡學習過程是一個對連接權值和閾值不斷修正的過程[9]；其次，進行模型預測控制(MPC)，即該系統辨識網絡模型能夠預測系統未來的性能，并在預測過程中找到最優算法以優化模型性能。

優化步驟為：

1)確定BP神經網絡的結構，從而確定輸入節點數和隱藏層節點數。

2)優化BP神經網絡。針對梯度下降法局部最小值、收斂速度較慢等問題，提出基于BP神經網絡LM算法的風向預測優化模型。

3)偏航控制策略優化及建模與仿真。優化后的偏航控制策略原理圖及流程圖分別如圖10、圖 11 所示。圖中：θp、θcon、θpre、θset分別指機艙位置角、平均風向角、風向預測角、偏航誤差設定閾值。

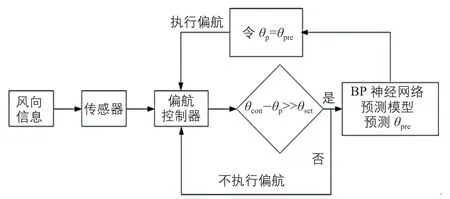
圖10 優化后的偏航控制策略原理圖Fig. 10 Schematic diagram of optimized yaw control strategy

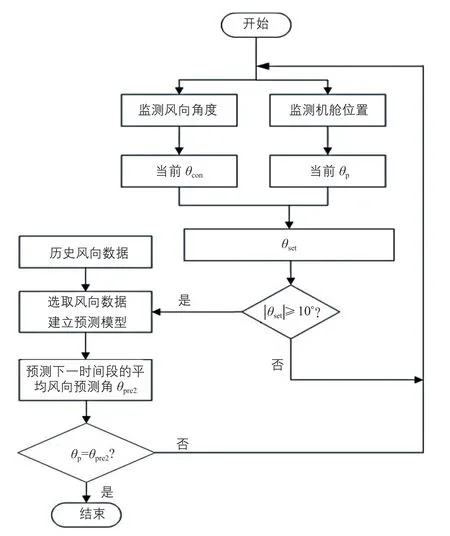
圖11 優化后的偏航控制策略流程圖Fig.11 Flow chart of optimized yaw control strategy

①數據采集。以某風電場中的101#風電機組(1.5 MW)作為數據采集樣機。該風電機組所在地的地形復雜、風況穩定性差，其數據具有很強的代表性。

②建模與仿真分析。風向預測優化模型的主要參數如表1所示，共對應4組數據。

搭建MATLAB仿真模型，根據表1中的4組數據，進行4次仿真，分別為仿真1～仿真4。仿真結果顯示：仿真1迭代 49次達到了全局誤差0.0001的要求，相關系數為0.99944，表明輸出誤差對期望輸出誤差跟蹤較好，相關性滿足要求。仿真2迭代17次達到全局誤差要求，相關系數為0.99949，相較于仿真1，迭代次數下降32次，這說明隱藏層節點數的增加提高了模型預測速度。仿真3得到的相關系數進一步提高為 0.99999，迭代次數也進一步降低，說明輸入層節點增加進一步提高了預測模型的預測性能。對比仿真3和仿真4發現，仿真4可以更快訓練樣本，使其達到要求的精度。因此采用仿真4的神經網絡結構作為風電機組風向預測優化模型的結構。

表1 風向預測優化模型的主要參數Table 1 Wind speed prediction optimization model parameters

對風向預測優化模型的預測數據進行分析并繪制預測值與實際值的預測誤差變化圖，如圖12所示。

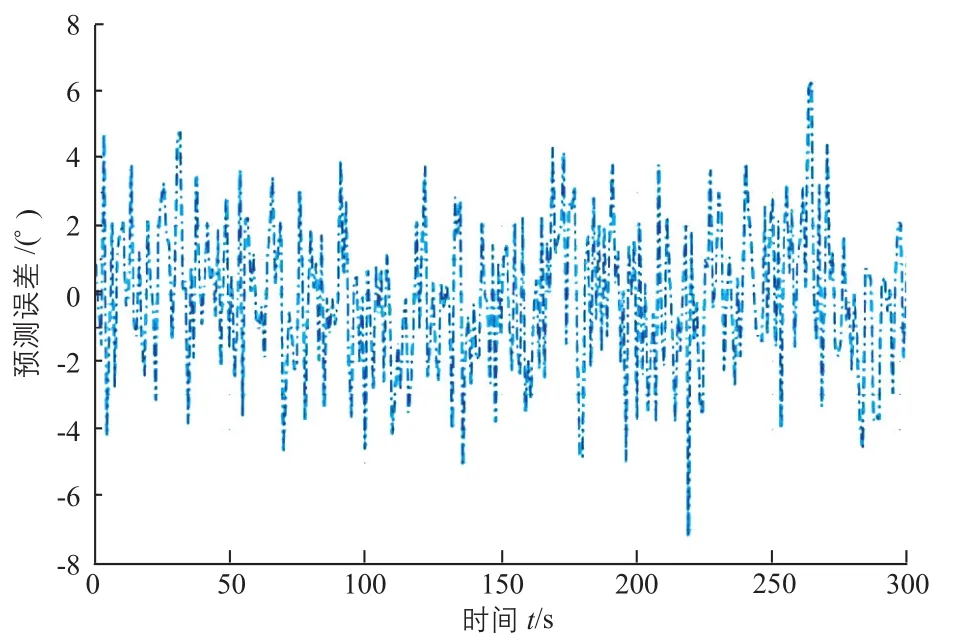
圖12 預測值與實際值的預測誤差變化圖Fig. 12 Variation diagram of prediction error between predicted value and actual value

2.3.2 偏航重啟對風優化策略

結合實際測風塔的風速數據，進行額定風速以下時的偏航重啟對風優化，具體步驟為：

1)采集上述風電場區域內1#、2#測風塔65 m高度處的風速數據。1#測風塔測得的風速在5 m/s時的頻率最高，為11.16%；風能在風速12 m/s時的占比最大，為11.0%。2#測風塔測得的風速在5 m/s時的頻率最高，為10.83%；風能在風速11 m/s時的占比最大，為10.8%。

2)結合風速頻率、風能占比分布情況，進行偏航重啟對風優化，具體方式為：

①將切入風速到額定風速區間共分為3個風速區間，分別為：3.0～5.0 m/s、6.0～8.0 m/s、9.0～12.5 m/s。

②根據風速頻率、風能占比的不同設定相應的偏航控制參數。其中，3.0～5.0 m/s風速頻率高、風能占比低，減少偏航次數即增大偏航誤差設定閾值；6.0～8.0 m/s風速頻率高、風能占比較低，保持偏航次數穩定；9.0～12.5 m/s風速頻率較高、風能占比高，采取積極的偏航策略、減小偏航誤差設定閾值，以最大程度捕獲風能。具體設定方法如表2所示。

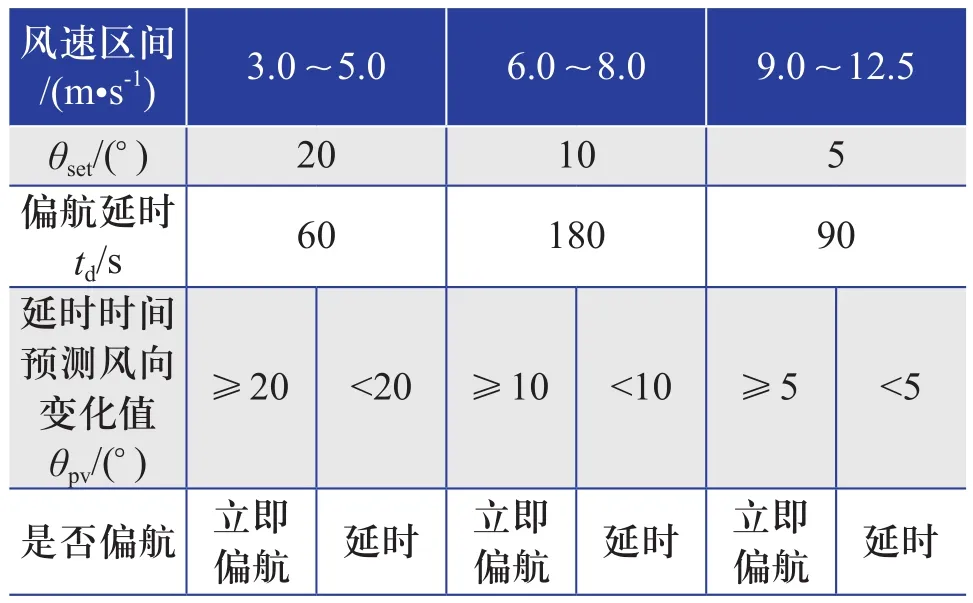
表2 偏航控制參數設定方法Table 2 Yaw control parameter setting method

3)仿真驗證及分析。優化后的偏航重啟對風策略原理圖及流程圖分別如圖13、圖14所示。

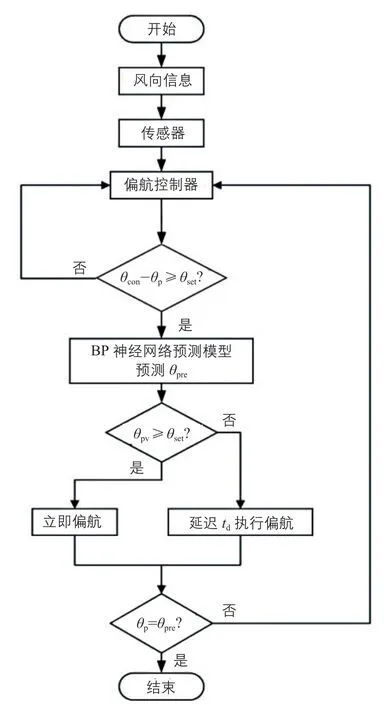
圖13 優化后的偏航重啟對風策略原理圖Fig.13 Schematic diagram of optimized yaw restart wind control strategy

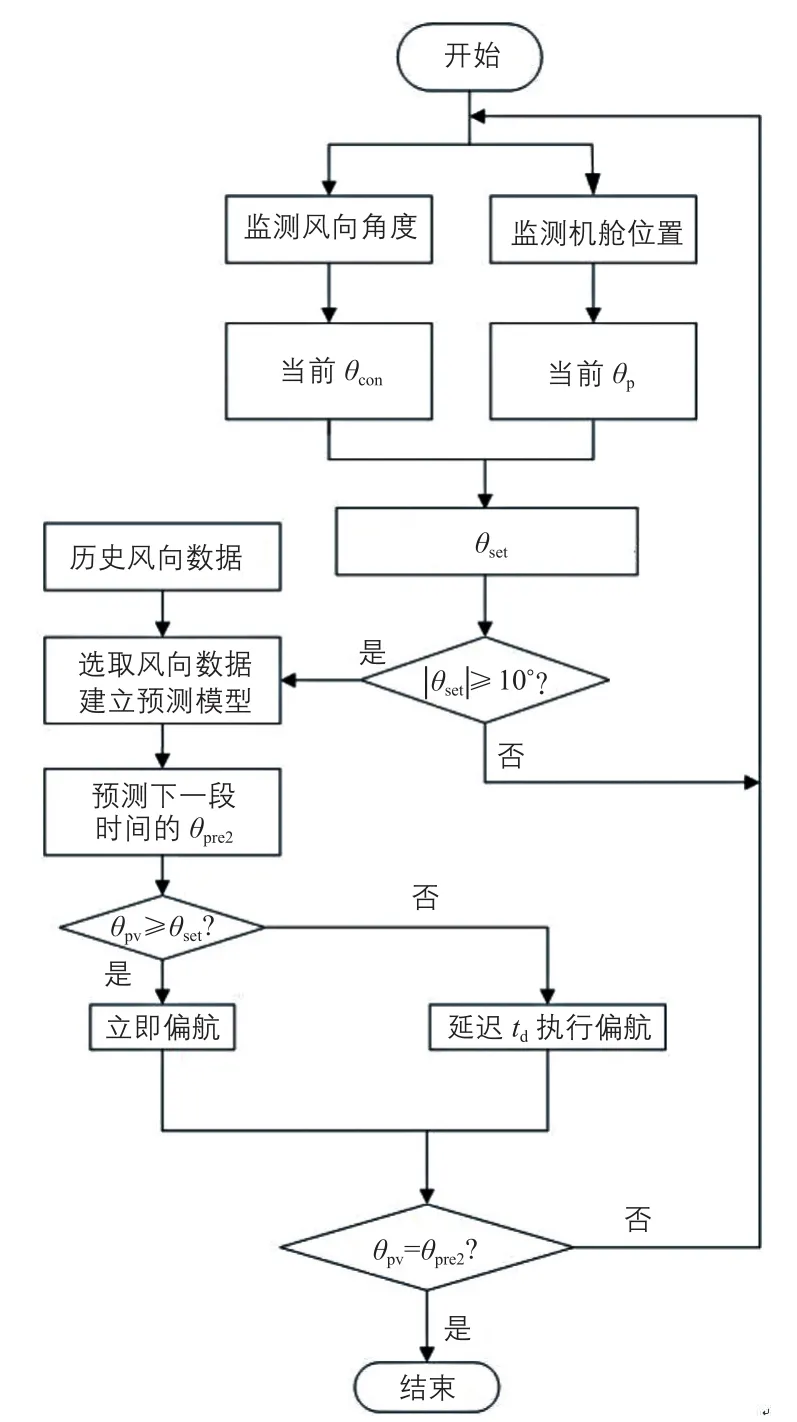
圖14 優化后的偏航重啟對風策略流程圖Fig. 14 Flow chart of optimized yaw restart wind control strategy

從表2中選取偏航控制參數，并進行仿真驗證。選取的偏航控制參數為：風速區間取6.0～8.0 m/s、θset=10°、td=180 s且偏航延時。繪制偏航控制參數優化前、后偏航次數及風電機組輸出功率對比圖，具體如圖15、圖16所示。

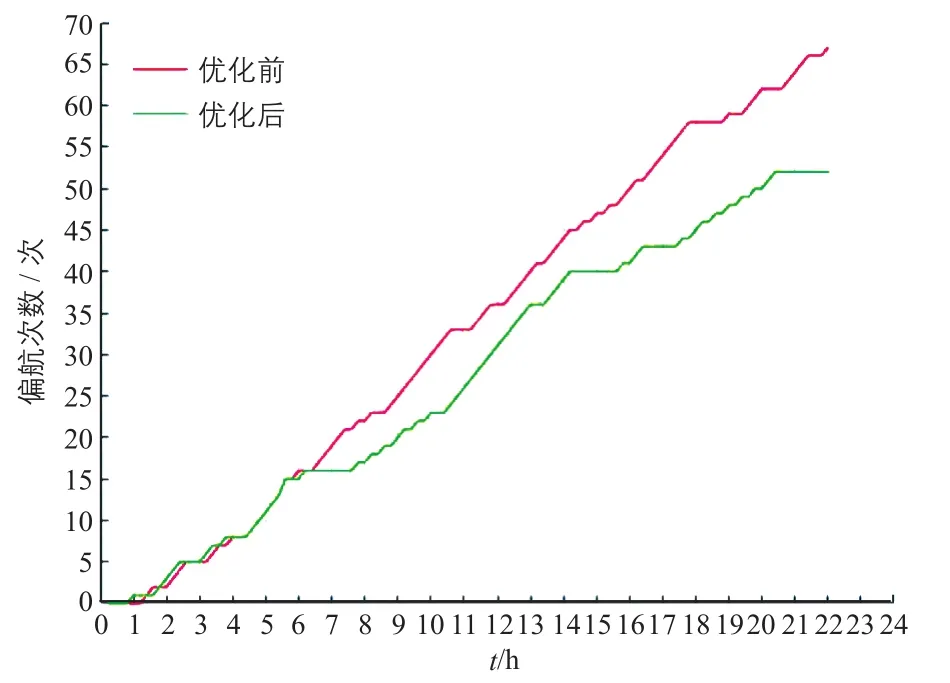
圖15 優化前、后偏航次數對比Fig. 15 Comparison of yaw times before and after optimization

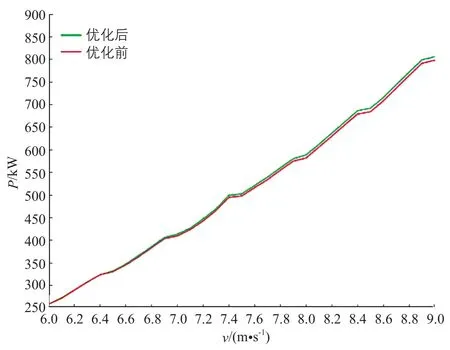
圖16 優化前、后風電機組輸出功率曲線對比Fig.16 Comparison of output power curves of wind turbines before and after optimization

由圖15、16可知：偏航控制參數優化后，偏航次數減少了15次，輸出功率非但沒有減少，還有微量增加。這說明偏航重啟對風優化策略提高了對風精度，減少了無效偏航次數。

3 結論

隨著風電上網電價逐步取消補貼、維護成本增加，提高風電場經濟效益對風電機組偏航控制系統提出了更高要求。本文針對傳統偏航系統靈活性差、響應滯后、對風精度低及無效偏航次數多等問題，對偏航誤差產生機理進行分析，并提出了相應調整策略，得到以下結論：

1)針對偏航靜態誤差產生機理，提出基于激光雷達的調整策略和基于最佳葉尖速比風向補償因數修正的調整策略，并通過試驗驗證了所采取策略可有效減小偏航靜態誤差。

2) 針對偏航控制策略誤差產生機理，提出基于BP神經網絡LM算法的風向預測優化模型。該模型能夠有效預測風向且訓練時間短、收斂速度快，將其應用于偏航控制策略優化，通過仿真驗證了該優化策略的有效性。

3)提出偏航重啟對風優化策略，通過仿真驗證了在不降低風電機組輸出功率的同時，可有效減少無效偏航次數，降低偏航機械部件磨損，延長使用壽命。