一種求解風電機組最優輪轂高度的數學模型

袁宗濤

(北京瑞科同創能源科技有限公司，北京 100075)

0 引言

輪轂高度的選擇是風電機組選型的重要環節。隨著中國風電行業平價時代的到來，為了應對電價和風資源水平雙降對風電行業帶來的挑戰，高輪轂機型將會大量出現，這對輪轂高度選擇方法的科學性和嚴謹性提出了更高要求。

該研究假設在一定邊界條件下存在最優輪轂高度，并且給出數學模型。但是受限于設備制造水平和風電機組塔架高度定制化的局限性，實際情況往往是在風電機組廠家提供的若干種塔架高度中擇優選用。目前輪轂高度比選的研究偏向于案例分析，缺乏理論模型支撐，科學性和嚴謹性不足。主要存在如下問題：1)不能確定在可選輪轂高度之外是否存在更優輪轂高度，常規方法不能科學地掌握輪轂高度與對其選擇造成影響的各因素之間的關系；2)當可選輪轂高度較多時，常規方法需要對每一種輪轂高度下風電機組的經濟性進行單獨測算，擇優選取，導致工作量大、效率低。

本文旨在建立一種求解風電機組最優輪轂高度的數學模型，并給出具有普適性的輪轂高度比選方法。從相對輪轂高度的邊際收益模型和邊際成本模型的建立展開研究，邊際收益模型的建立涉及功率曲線、風廓線和風速分布模型，重點在于建立風電機組年均發電量與輪轂高度之間的函數關系，在一定電價和折現率下確定相對輪轂高度的邊際收益現值；邊際成本模型的重點在于建立塔架質量與輪轂高度之間的函數關系，通過計算固定成本和可變成本求得相對輪轂高度的邊際成本；通過模型最終得到風電機組的最優輪轂高度。基于最優輪轂高度給出3種最佳輪轂高度比選方法，提高了輪轂高度比選方法的科學性和嚴謹性。

1 模型概述

輪轂高度的比選實質上是風電機組經濟性的比選，最優輪轂高度即風電機組收益最大化時對應的輪轂高度。一般情況下，風電機組的總收益會隨著輪轂高度的提升而增加，但同時其建設成本也會增加。

本文假設存在某個輪轂高度，使風電機組的凈收益最大，此輪轂高度即為最優輪轂高度，即式(1)有解。

式中：h為風電機組的輪轂高度，m；g(h)為關于輪轂高度的風電機組的凈收益函數；CI(h)為現金流入，表示關于輪轂高度的風電機組總收益函數；CO(h)為現金流出，表示關于輪轂高度的風電機組總支出或總成本函數；Gmax為風電機組的最大凈收益，萬元。

進一步將問題轉化為求解式(2)：

式中：g(h)′為g(h)的一階導數。

即：

式中：CI(h)′為CI(h)的導數，表示相對輪轂高度的邊際收益；CO(h)′為CO(h)的導數，表示相對輪轂高度的邊際成本。

2 相對輪轂高度的邊際收益

風電機組總收益CI的計算式為：

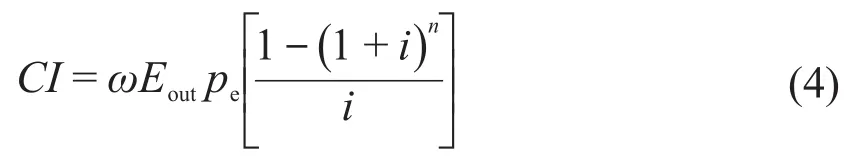
式中：ω為風電機組發電量折減系數，取值通常介于0.7～0.8之間，為無量綱常數；Eout為風電機組年均理論發電量，kWh；pe為售電電價，元/kWh；i為折現率，%；n為折現年數或風電機組運行年數。

關于風速v的風電機組年均理論發電量函數Eout(v)的計算式為：

式中：T為一年的小時數，h，取值為8760；vci為切入風速，m/s；vco為切出風速，m/s；vr為額定風速，m/s；Pf(v)為風速介于切入風速和額定風速之間時風電機組的功率曲線函數；f(v)為風速的密度分布函數；P(v)為不同風速段下風電機組的輸出功率函數；Pr為風電機組的額定功率，kW。

為確定風電機組總收益與輪轂高度之間的關系，需要把式(5)的積分結果轉化為關于輪轂高度的函數，即：

結合式(4)、式(6)，即可得到風電機組邊際收益與輪轂高度的函數關系，即：

2.1 功率曲線

風電機組的輸出功率特征通常用功率曲線來表示，其在不同風速段的輸出功率特征如式(8)所示[1-2]：

當風速小于切入風速時，風電機組不啟動，此時其輸出功率為零；在風速介于額定風速和切出風速之間時，風電機組按照額定功率滿功率運行；當風速大于切出風速時，風電機組停機，此時其輸出功率為零；在風速介于切入風速和額定風速之間時，功率曲線主要取決于風電機組的功率控制，此時功率曲線的表現要比其他風速段都要復雜，此風速段的風電機組功率曲線也是數學模型的核心所在。

風速介于切入風速和額定風速之間時的風電機組功率曲線數學模型有多種，文獻[1-3]都對此類數學模型進行過研究，但是由于其復雜性，導致這些研究的結論并不完全一致。文獻[2]將9種數學模型應用到32臺商用風電機組的功率曲線分析，并進行對比研究，研究后發現，基于功率因數的模型(power cofficient model)和通用數學模型(general model)的相對誤差最小。本研究認為，相比于其他研究，文獻[2]的研究樣本更多，論證相對更充分，適用性更廣，因此本文采用通用數學模型來模擬風速介于切入風速和額定風速之間時風電機組的功率曲線。該通用數學模型可表示為：

式中：k為功率曲線的冪次，本文取值為1.2。

以某單機容量為3000 kW、葉輪直徑為155 m的風電機組(下文簡寫為“155-3000風電機組”)為例，采用通用數學模型模擬的風電機組功率曲線(k=1.2，Pr=3000)及理論功率曲線如圖1所示。

圖1 某155-3000風電機組的理論功率曲線及模擬功率曲線Fig. 1 Theoretical power curve and simulated power curve of a 155-3000 wind turbine

2.2 風廓線

在風資源評估中，風廓線用來描述風速隨高度的變化規律。應用比較廣泛的風廓線模型有冪律風廓線模型和對數風廓線模型，本文采用冪律風廓線模型。該模型可表示為：

式中：Vave為年均風速，m/s；α為切變指數，為無量綱；β為常數。

本文后續案例分析中探討了在輪轂高度風速一定的前提下，切變指數對輪轂高度選擇的影響，則式(10)可變形為：

式中：Vhub為輪轂高度的年均風速，m/s；z為距離地表的高度，m。

2.3 風速分布

風速的密度分布函數通常采用雙參數的威布爾分布，為簡化數學模型，本文采用形狀參數q=2時的威布爾分布，即瑞利分布，可表示為：

式中：σ為尺度參數，m/s；e為自然常數。

根據瑞利分布密度函數，尺度參數和年均風速的關系可表示為：

不同年均風速下的瑞利分布如圖2所示。

圖2 不同年均風速下的瑞利分布Fig. 2 Rayleigh distribution under different annual average wind speeds

結合風廓線模型，可將輪轂高度作為參數引入瑞利分布密度函數，進而引入收益模型。根據式(12)、式(13)可得：

3 相對輪轂高度的邊際成本

風電機組的總成本由固定成本和可變成本構成。其中，固定成本不隨風電機組輪轂高度的變化而變化，是由風電機組的裝機容量和單位千瓦造價相乘得出；本文提出的風電機組最優輪轂高度數學模型重點關注可變成本部分。

風電機組的總成本模型可表示為：

式中：pfix為風電機組的單位千瓦造價，元/kW；pvar為風電機組單位高度塔筒的造價，元/m；Mtwr(h)為關于輪轂高度的塔筒質量函數，kg。

塔筒形式與結構多種多樣[4-5]，本研究基于應用最為廣泛的鋼制錐形塔筒進行研究設計。由于該種形式的塔筒主要是按質量計價，在單價固定的前提下，關鍵是確定塔筒質量和其高度之間的關系。但是，即便是錐形塔筒，其設計形式也不一而足[5-6]，直接建立數學模型會比較困難。因此為簡化模型，本研究選取了42種當下主流的風電機組機型及其塔筒作為樣本，選用5種模型對這42種主流機型輪轂高度與塔筒質量之間的關系進行擬合，然后擇優選取。

這5種模型分別是：二次多項式模型、三次多項式模型、對數模型、冪律模型和指數模型。采用不同模型時輪轂高度-塔筒質量的擬合函數如式(16)～式(20)所示。

二次多項式模型的擬合函數為：

式中：c1、c2均為系數。

三次多項式模型的擬合函數為：

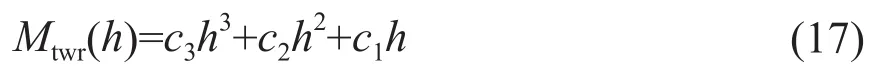
式中：c3為系數。

對數模型的擬合函數為：

冪律模型的擬合函數為：

指數模型的擬合函數為：

5種模型得到的輪轂高度-塔筒質量擬合函數的參數估計值如表1所示，擬合曲線圖形如圖3所示。

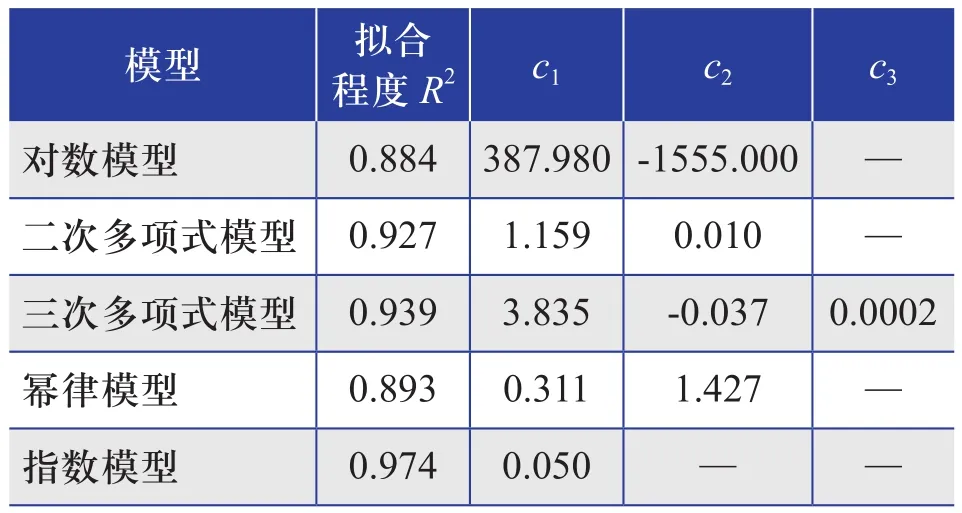
表1 5種輪轂高度-塔筒質量擬合函數的參數估計值Table 1 Parameter estimation of five fitting functions of hub heights-tower mass

圖3 5種輪轂高度-塔筒質量的擬合曲線對比Fig. 3 Comparison of five fitting curves of hub heights-tower mass

從擬合優度、預測準確度和模型簡潔性3個方面進行綜合考慮后，本文采用二次多項式模型。由式(15)、式(16)可得到風電機組的邊際成本CO(h)′與風電機組輪轂高度的函數關系，即：

4 最優輪轂高度及最佳輪轂高度比選方法

當風電機組的邊際收益等于邊際成本時，此時項目的凈收益最大，可求得風電機組的最優輪轂高度h0。即，當h=h0時，下式成立：

需要注意的是，此時得到的最優輪轂高度為理論計算值。在實際工程應用中，通常是在風電機組出廠標配的有限的若干種輪轂高度中擇優選取，作為最佳輪轂高度hbt。下文提出3種輪轂高度比選方法，所得輪轂高度即為最佳輪轂高度(即相對最優)；最佳輪轂高度可以與最優輪轂高度相同，也可以不相同。

假設某種風電機組機型的可選輪轂高度為ht(t=1, 2, 3, …,m)，且ht+1＞ht，可通過直接計算法、判別法、快速近似判別法3種算法解得風電機組最佳輪轂高度。

1)直接計算法。通過Max[g(ht)]得到的輪轂高度即為最佳輪轂高度，但此方法需要對所有備選輪轂高度進行逐次計算。

2)判別法。當h0≥hm時，則風電機組最佳輪轂高度為hm；當h0≤h1時，則風電機組最佳輪轂高度為h1；當h1≤hj≤h0≤hj+1≤hm(j為緊鄰h0的那個高度的編號)時，則風電機組最佳輪轂高度為hj或hj+1，此時可轉為直接計算法或快速近似判別法求解。

3)快速近似判別法。此方法假定g(h)在可行域內以h=h0為軸對稱，則Min|ht-h0|對應的輪轂高度即為最佳輪轂高度。此方法可描述為“距離最優輪轂高度最近者為最佳”。

當可選輪轂高度的最大值小于等于最優輪轂高度時，最大值為最佳輪轂高度；當可選輪轂高度的最小值大于等于最優輪轂高度時，最小值為最佳輪轂高度。若可選最佳輪轂高度大于最優輪轂高度，則必定存在1個小于最優輪轂高度且收益相同的高度， 可近似為最優輪轂高度的對稱高度(即2h0-hbt)。

5 算例

假設某風電場140 m高度的年均風速為6 m/s，服從瑞利分布，切變指數為0.14；選用某廠家制造的155-3000風電機組機型，按照前文所述方法計算該風電機組的最優輪轂高度，同時在給定的幾種風電機組輪轂高度中選擇最佳輪轂高度。計算時各參數取值如表2所示。

表2 計算中的參數取值Table 2 Parameter value in calculation

表3 計算結果Table 3 Calculation results

風電場達到第1個盈虧平衡點和第2個盈虧平衡點時，其總收益與總成本相等。風電場的總收益和總成本與風電機組輪轂高度的關系曲線如圖4所示。

圖4 風電場的總收益、總成本與輪轂高度的關系曲線Fig. 4 Relationship curve between total revenue and total cost of wind farm and hub height

最優輪轂高度時風電場的凈收益最大。風電場的凈收益與風電機組輪轂高度的關系曲線如圖5所示。

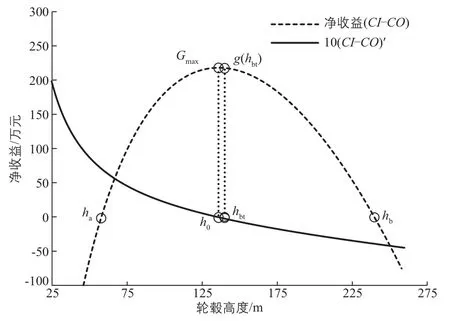
圖5 風電場的凈收益與輪轂高度的關系曲線Fig. 5 Relationship curve between net income of wind farm and hub height

不同切變指數取值下的最優輪轂高度的變化情況如圖6所示，不同塔筒單位造價下的最優輪轂高度的變化情況如圖7所示。

圖6 不同切變指數取值下的最優輪轂高度的變化情況Fig. 6 Variation of optimal hub height under different shear index values

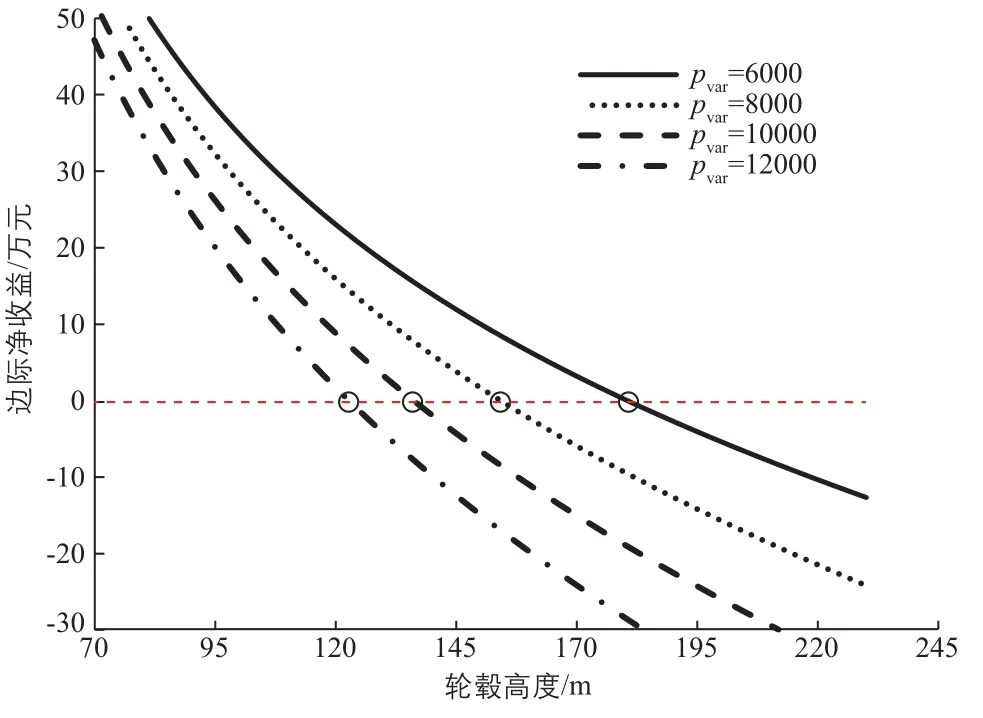
圖7 不同塔筒單位造價下的最優輪轂高度的變化情況Fig. 7 Variation of optimal hub height under different unit cost of tower

由圖6可以看出：曲線上邊際凈收益為零時對應的輪轂高度即為最優輪轂高度，隨著切變指數取值的增大，最優輪轂高度也在增加。

由圖7可以看出：曲線上邊際凈收益為零時對應的輪轂高度即為最優輪轂高度，隨著塔筒單位造價的提高，最優輪轂高度逐漸減小。

6 結論

本文建立了一種求解風電機組最優輪轂高度的數學模型，并給出了具有普適性的輪轂高度比選方法。通過建立模型，確定輸入參數，經過算例驗證，得到以下結論：

1)在可行域內，風電機組存在最優輪轂高度且值為唯一。

2)當可選輪轂高度的最大值小于等于最優輪轂高度時，最大值為最佳輪轂高度；當可選輪轂高度最小值大于等于最優輪轂高度時，最小值為最佳輪轂高度。若可選最佳輪轂高度大于最優輪轂高度，則必定存在1個小于最優輪轂高度且收益相同的高度。即若最佳輪轂高度大于最優輪轂高度，在獲得同等收益的前提下其必定可以優化，以減少資源浪費。

3)最優輪轂高度與切變指數成正比，與塔筒單位造價成反比，與風電機組的固定成本無關。