關于方程的一個注記
董 坤, 廖群英, 張夢蝶
(四川師范大學 數學科學學院, 四川 成都 610066)
1 引言及主要結果
歐拉函數φ(n)(n∈Z+)作為數論中一個非常重要的函數,早在18世紀就由著名數學家歐拉提出,定義為

即1,2,…,n中與n互素的個數[1].關于歐拉函數的研究歷來備受關注.文獻[2-6]為將Lehmer同余式從模素數的平方推廣到模任意正整數的平方,引進了正整數的廣義歐拉函數
φ
并給出了φe(n)(n=3,4,6)的準確計算公式.人們也希望利用廣義歐拉函數的準確計算公式來討論一些不定方程的解.近年來,文獻[7-9]給出了方程

對正整數
記
并規定Ω(1)=ω(1)=0.
為敘述方便,設正整數n>6,且
n=2α3
其中,α,β,αi≥0,pi為素數且5≤p1 當α=β=0時,ω(n)=k;當α、β僅有一個為0時,ω(n)=k+1;當αβ≠0時,ω(n)=k+2. 定理 1.1當以下條件之一成立時: (Ⅰ)α=0,β∈{0,1}且pi≡5(mod6); (Ⅱ)α=1,β∈{0,1}且pi≡5(mod6); (Ⅲ)α≥2,β∈{0,1},k=1且p1≡5(mod6); (Ⅳ)β≥2或存在pi≡1(mod6), (n,d)= 為證明本文的主要結果,需要如下引理. 引理 1.2[4] φ6(n)= 情形Ⅰ 若α=β=0且 pi≡5(mod6), 1≤i≤k, (i) 當k≥2時,對比等式兩邊奇偶性可知方程無解. 從而原方程等價于 pα1-11(p1-1)+4(-1)α1=6pα1-θ11. 若α1>θ1,則α1≥2,從而p1|4,與p1≥5矛盾,故α1=θ1,即 pα1-11(p1-1)+4(-1)α1=6. (1) 當α1=1時,代入方程(1)解得p1=11,即 (n,d)=(11,11); 當α1≥2時,因為p1≥5,所以 從而此時方程(1)無解. 經檢驗(n,d)=(11,11)是原方程的解. 情形Ⅱ 若α=0,β=1且 pi≡5(mod6), 1≤i≤k, 對比等式兩邊奇偶性可知此時方程無解. 情形Ⅲα=1,β=0且 pi≡5(mod6), 1≤i≤k, 2θpα1+θ1-11(p1-1)+2θ+1pθ11(-1)α1+1=12pα11.(3) 若α1≥2,由方程(3)可知 2θpα1-11(p1-1)+2θ+1(-1)α1+1=12. (4) 因為p1≥5,所以 從而方程(4)在α1≥2時無解,故α1=1,此時方程(3)即為 2θpθ11(p1-1)+2θ+1pθ11=12p1, 故(θ,θ1)=(0,1)時,p1=11,即 (n,d)=(22,11); (θ,θ1)=(1,1)時,p1=5,即 (n,d)=(10,10); (θ,θ1)=(1,0)時,無解. (-1)α1+α2)=3pα11pα22. 對比等式兩邊奇偶性可知2?d.因為d|n且d>2,故可設 且θ1、θ2不同時為0,從而原方程等價于 pθ1-11pθ2-12(p1-1)(p2-1)- 4(-1)α1+α2pθ1-α11pθ2-α22=12. (5) 當θ1θ2≠0時,因為p2>p1≥5,所以 從而此時方程無解,故θ1、θ2恰有一個為0. 當θ1=0,θ2≥1時,若θ2≥2,因為 p2≡5(mod6) 且p2>p1≥5,所以p2≥11,從而由 可知此時方程無解,故θ2=1,代入方程(5)可得 pα1-11pα2-12(p1-1)(p2-1)+ 4(-1)α1+α2+1=12pα11pα2-12. (6) 若存在αi≥2,則pi|4,此時無解;若α1=α2=1,代入方程(6)可得 p1p2-13p1-p2-3=0. 將p2=13代入可知無解,所以 因為p1≥5,所以p2-13=1,2,4;又因為 p2≡5(mod6), 所以p2=17,p1=5,即(n,d)=(170,17). 當θ2=0,θ1≥1時,若θ1≥2,由p2≥11,p1≥5可知 從而此時方程無解,故θ1=1,代入方程(5)可得 pα1-11pα2-12(p1-1)(p2-1)+ 4(-1)α1+α2+1=12pα1-11pα22. (7) 若存在αi≥2,則pi|4,此時無解;若α1=α2=1,代入方程(7)可得 p1p2-13p2-p1-3=0, 解得p1=17,p2=5,與p1 (iii) 當k≥3時,對比等式(2)兩邊奇偶性可知此時方程無解. 經檢驗 (n,d)=(22,11),(10,10),(170,17) 均是原方程的解. 情形Ⅳ 若α=1,β=1且 pi≡5(mod6), 1≤i≤k, (-1)Ω(n)2 (8) (9) 從而此時方程無解,故α1=1,此時方程(9)即為 d(p1-2)=18p1. 因為 gcd(p1-2,p1)=1, 所以p1|d,d=2p1或6p1.當d=2p1時,解得p1=11,即(n,d)=(66,22);當d=6p1時,解得p1=5,即(n,d)=(30,30). (-1)α1+α2)=9pα11pα22. 對比等式兩邊奇偶性可知2?d.因為d|n且d>2,故可設 且θ、θ1、θ2不同時為0,從而原方程等價于 pα1+θ1-11pα2+θ2-12(p1-1)(p2-1)+ 2(-1)α1+α2pθ11pθ22=32-θ2pα11pα22. (10) 1) 當α1≥3時,由方程(10)可知θ1=α1.因為p1≥5,所以 從而此時方程無解. 2) 當α2≥2時,由方程(10)可知θ2=α2.因為p2≡5(mod6)且p2>p1≥5,所以p2≥11,從而 故此時方程無解. 3) 當(α1,α2)=(1,1)時,代入方程(10)可得 (p1-1)(p2-1)+2=32-θ2p1-θ11p1-θ22.(11) 當θ2=0時,p2|p1-3,與p2>p1矛盾;當θ2=1時,將(θ,θ1)=(0,0)代入方程(11)解得 (p1,p2)=(5,23), 即 (n,d)=(690,23); 將 (θ,θ1)=(0,1),(1,0),(1,1) 代入方程(11)可知此時方程均無解. 4) 當(α1,α2)=(2,1)時,代入方程(10)可得 p1(p1-1)(p2-1)-2=32-θ2p2-θ11p1-θ22.(12) 當θ1=0,1時,由方程(12)可知p1|2,與p1≥5矛盾;當θ1=2時,代入方程(12)可得 p1(p1-1)(p2-1)-2=32-θ2p1-θ22. (13) 將(θ,θ2)=(0,0)代入方程(13)解得 (p1,p2)=(5,11), 即 (n,d)=(1650,25); 將 (θ,θ2)=(0,1),(1,0),(1,1) 代入方程(13)可知此時方程均無解. (iii) 當k≥3時,對比等式(8)兩邊奇偶性可知此時方程無解. 經檢驗 (n,d)=(66,22),(30,30),(690,23),(1650,25) 均是原方程的解. 情形Ⅴ 若α≥2,β=0,k=1且 p1≡5(mod6), 且θ、θ1不同時為0. 2α-2-(-1)α=3·2α-θ. (14) 對比等式兩邊奇偶性可知α=θ,代入方程(14)可得 2α-2-(-1)α=3, 解得α=3或4,即(n,d)=(8,8)或(16,16). (ii) 當α1=1時,原方程等價于 2α-3(p1-1)-(-1)α+1=2α-1-θ3p1-θ11. (15) 對比等式兩邊奇偶性可知 α-1-θ=0 當α-1-θ=0時,若θ1=0,則有 (2α-1-12)p1=2α-1+4(-1)α+1, 解得(p1,α)=(5,5),即 (n,d)=(160,16); 若θ1=1,則有 2α-1p1=2α-1+4(-1)α+1+12, 解得(p1,α)=(5,2)或(5,3),即(n,d)=(20,10)或(40,20). 當α=2,θ=0時,代入方程(15)可得 若θ1=0,則p1|p1+1,矛盾,故θ1=1,解得 (p1,α)=(11,2), 即(n,d)=(44,11). 2α-1pα1-11(p1-1)-4(-1)α+α1=2α+1-θ3pα1-θ11. 若α1>θ1,則p1|4,與p1≥5矛盾;若α1=θ1,則 因為α≥2,p1≥5,所以 故此時方程無解. 經檢驗 (n,d)=(8,8),(16,16),(160,16), 均是原方程的解. 情形Ⅵ 若α≥2,β=1,k=1且p1≡5(mod6),即因為d|n且d>2,故可設 且θ、γ、θ1不同時為0. 3γ(2α-1-(-1)α+1)=2α-θ32. (16) 對比等式兩邊奇偶性可知α=θ,代入方程(16)可知 3γ(2α-1-(-1)α+1)=9, 解得(α,γ)=(2,1),(3,1)或(4,0),即(n,d)=(12,12),(24,24)或(48,16). 2α-2(p1-1)-(-1)α=2α-θ-132-γp1-θ11.(17) 對比等式兩邊奇偶性可知α=1+θ,代入方程(17)可得 2α-2(p1-1)-(-1)α=32-γp1-θ11. (18) 當θ1=0時,若α≥6,則由 2α-2(p1-1)>10p1>9p1+1 可知此時方程無解,故α=2,3,4,5,分別代入方程(18)解得 (p1,α,γ)=(5,4,1), 即 (n,d)=(240,24). 當θ1=1時,若α≥4,因為p1≥5,所以由 可知此時方程無解,故α=2,3,分別代入方程(17)解得(p1,α,γ)=(5,2,1),(11,2,0)或(5,3,0),即(n,d)=(60,30),(132,22)或(120,20). 2α-2pα1-11(p1-1)-(-1)Ω(n)= (19) 對比等式兩邊奇偶性可知α=1+θ,代入方程(19)可得 2α-2pα1-11(p1-1)-(-1)Ω(n)=32-γpα1-θ11. 因為α1≥2,所以θ1=α1,又因為p1≥5,所以由 可知此時方程無解. 經檢驗 (n,d)=(12,12),(24,24),(48,16), 均是原方程的解. 情形Ⅶ 若β≥2或存在pi≡1(mod6),則此時方程等價于 dφ(2α3 對比等式兩邊奇偶性可知有以下3種情形: 當β=0時,k=1或2,此時若α=0,解得(n,d)=(7α1,7);若α≥1,解得(n,d)=(2α7α1,14)或(2α13α1,13). 當β=1時,k=0或1,此時若α=0,方程無解;若α≥1,解得(n,d)=(2α3·19α1,19)或(2α3·7α1,21). 當β≥2時,k=0或1,此時若α=0,解得(n,d)=(3β,9);若α≥1,解得(n,d)=(2α3β,18),(2α3β19α1,19)或(2α3β7α1,21). 經檢驗 (n,d)=(7α1,7),(2α7α1,14),(2α13α1,13), 均是原方程的解,其中α,β,α1≥1,β1≥2.
2 主要結果的證明


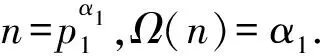
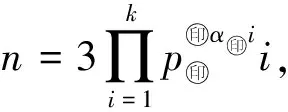






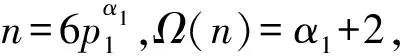





(20,10),(40,20),(44,11)


(240,24),(60,30),(132,22),(120,20)
(3β1,9),(2α3β1,18),
(2α3β19α1,19),(2α3β7α1,21)

