多機器人協作的靈活性分析與仿真

陶平 鄒成文 王天瑞

（①武漢科技大學冶金裝備及其控制教育部重點實驗室，湖北 武漢 430081；②武漢科技大學機械傳動與制造工程湖北省重點實驗室，湖北 武漢 430081）

現代工業中，多機器人協作系統具有更高的自由度、較大負載能力和靈活操作方式，可以完成更加復雜的任務。多機器人協作系統的運動靈活性反映了協作系統整體協調操作的運動能力，其機械臂的協調運動靈活性直接影響協作系統的整體運動性能[1]。

目前國內外學者對機械臂的靈活性進行了大量的研究，李憲華[2]采用基于雅克比SVD可操作度的指標，評估了單機械臂的操作能力。符曉[3]利用雅克比矩陣條件數，求出6R機器人在工作空間內各處的奇異度，并將其可視化。孫青[4]針對雙臂6R服務機器人，進行了靈活性分析，研究了雙臂在協調操作過程中的奇異性和靈活性。潘建龍[5]闡述了多機器人協作時可操作度的定義，對多機器人焊接系統進行了最優軌跡的規劃。Paul R P等[6]針對非冗余度機器人的運動特點，采用雅可比矩陣的行列式分析出腕關節的位姿。Yang D C H等[7]對機器人條件數進行了定義，Angeles J等[8]將條件數作為機器人靈活性的評價指標，并將這一指標用來分析機器人動力學性能。當前，多機器人協作大多集中在雙機器人協作的研究上，國內對多機器人協調操作的靈活性研究較少。

基于以上分析，本文針對多機器人系統在工業應用中的運動特征，選用可操作度為機器人靈活性評價指標，并根據該指標的定義分析得到多機器人系統整體可操作度的數學評價模型。同時提出了一種求取機器人在單位節點多姿態下的加權可操作度數值的算法，采用該算法計算多機器人系統在協作空間內的整體可操作度，并將多機器人系統的靈活性可視化表達出來，由此得到靈活性較高的區域，為以后的多機器人協調運動的軌跡規劃打下基礎。

1 多機器人系統模型

1.1 運動學分析

以3個六自由度的IRB1410機器人組成的多機器人焊接系統為研究對象。在該系統中，其中2個機器人1和2起搬運作用，將工件夾持到工作空間中，而焊接機器人3則對工件進行焊接操作，多機器人協作焊接系統圖如圖1所示。

圖1 多機器人協作系統示意圖

多機器人協作系統進行作業時，各機器人的基座位置固定，其相對位置始終不變，即{B1}、{B2}、{B3}固定，機器人基坐標系到世界坐標系{W}的齊次變換矩陣是一個定值。作業中，2個搬運機器人1和2夾持工件，兩搬運機器人之間的運動關系存在緊協調運動關系；焊接機器人3進行焊接時，它與搬運機器人之間的運動關系是松協調運動關系，其協調關系如下：

（1）緊協調：兩搬運機器人搬運工件時存在，在該過程中，兩機器人之間無相對運動，相對位姿保持不變，速度保持同步，滿足關系

式中：x1、x2分別表示兩搬運機器人的末端位姿向量；U表示兩個搬運機器人之間的齊次變換矩陣。

（2）松協調：存在于焊接機器人與搬運機器人之間，滿足關系

式中：x3表示焊接機器人的末端位姿向量；α(t)表示搬運機器人與焊接機器人還存在相對運動，為時變向量。

1.2 協作空間分析

對其中的焊接機器人建立D-H坐標系，如圖2所示。由此得到D-H坐標參數，如表1所示。表1中，θi為第i個關節的角度值，di為相鄰關鍵之間的桿件長度，ai為相鄰關節之間的桿件偏移量，αi為相鄰坐標系之間的扭轉角。同理，2個搬運機器人的D-H坐標建立方法同上，在此不再贅述。

圖2 焊接機械臂D-H坐標系

表1 焊接機器人連桿D-H參數

利用Robotics工具箱，搭建多機器人協作系統模型的仿真平臺，如圖3所示。圖3中，兩搬運機械臂和焊接機械臂的基座坐標分別為(?1,?1,0)、(1,?1,0)、(0,1,0)。

圖3 多機器人協作系統模型

圖2中，d1=475mm，d4=720mm，d6=85mm，a1=150mm，a2=600mm，a3=120mm。

相鄰兩連桿之間的齊次坐標變換矩陣為

式中：cθi表示cosθi；cαi表示cosαi；sθi表示sinθi；sαi表示sinαi。

結合機械臂的正運動學方程、表1的參數和上面的公式，利用蒙特卡羅法，可以得到焊接機器人的工作空間，同理也可得到2個搬運機器人各自的工作空間，由3個機器人工作空間的交集得到協作空間的范圍，如圖4所示。

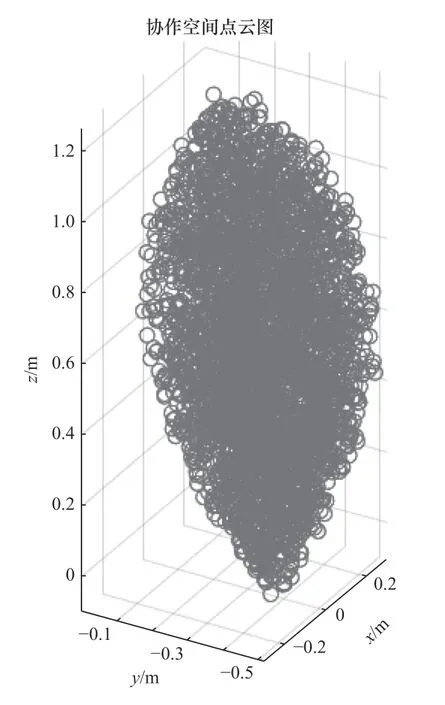
圖4 協作空間點云圖

2 多機器人靈活性評價

機器人運動靈活性評價指標，主要有條件數、可操作度及各向同性指標等，其中可操作度、條件數和最小奇異值是比較經典的3個靈活性評價指標[2]。可操作度作為衡量機器人靈活性的重要指標之一，被廣泛運用機器人尺寸優化、運動性能優化等各個方面，用來改善機器人的傳輸性能，從而提高工作效率[9?10]。

本文選取可操作度作為機器人執行任務時的靈活性評價指標。

2.1 機器人可操作度定義

可操作度定義為機器人對任意改變末端執行器位置和方向的能力，是一個非常重要的評價指標。可操作度越大，機器人從關節空間到工作空間運動的轉換能力就越強，靈活程度越好。

雅可比矩陣表示了機器人運動時自關節空間到操作空間的運動速度的傳遞關系，可得

式中：x為操作空間的坐標，x∈Rm,Rank(J(q))≤m，x˙為操作空間的速度；q為關節空間坐標，q∈Rn；q˙為關節空間的速度；J(q)為雅克比矩陣，J(q)∈Rm×n。

機器人可操作度的定義為

可操作度的大小表現了機器人在操作空間中各個方向傳遞速度的能力，根據可操作度的定義可知，當可操作度ω=0時，J(q)=0，機器人瞬時位于奇異位形。

2.2 多機器人可操作度

在多機器人協作工作時，協作系統靈活性反映了其整體的傳力和傳速性能。在協作系統中，存在緊協調和松協調兩種不同的協作關系，在計算可操作度時，先分別計算各自的可操作度，再計算協作系統的可操作度。

兩搬運機器人滿足緊協調關系時，兩機器人之間的運動可描述為

式中：J(q)1、J(q)2分別為兩搬運機器人的雅克比矩陣。

由此，得到兩搬運機器人的可操作度Mt的定義為

焊接機器人與搬運機器人之間的運動關系為松協調，需要單獨計算它的可操作度。

綜合上述考慮，得到多機器人協作時的可操作度MMR為

式中：α1為兩搬運機器人的靈活性系數，α2為焊接機器人的靈活性系數，根據系統中所有機器人可操作度橢球的體積交集大小占各個橢球體積的比值，可確定出α1和α2；Mt為兩搬運機器人的可操作度；Ml為焊接機器人可操作度。

3 多機器人協作空間靈活性分析

機器人的工作空間分為可達空間和靈巧空間。其中，可達空間即為機器人可以到達的所有點構成的空間；而靈巧空間為機器人以任意姿態能到達的點所構成的空間。機器人的奇異點指在工作空間中，由于機器人位于一些特殊位姿（如軸線相交或者平行等）關系時，機器人喪失1個或者多個自由度,導致機器人在某個方向上傳遞速度為0，即機器人在此時處于卡死狀態。根據前文的分析，當機器人處于奇異位形時，可操作度ω=0，可以得到此時機器人的雅可比矩陣J(q)=0，由矩陣的定義可知，Rank(J(q))

本文的研究中，將每個轉角分為11份，步長為0.2π，可以得到對應的位姿矩陣，根據算法可以計算出對應點的可操作度。本文首先分析了焊接機器人在工作空間內的可操作度，考慮到在z=0.69m的平面上，其工作空間面積最大，給出該平面內焊接機器人的可操作度分布情況，如圖5所示。圖5中，對該平面的x軸和y軸等間距劃分為21等份，所取得的樣本工作點共441個。利用網格節點的顏色來表征可操作度ωi的值，由此得到焊接機械臂在工作空間內其可操作度分布情況，其中右側的豎條表征了不同顏色所代表的可操作度值。

圖5 z=0.69m 平面下焊接機器人可操作度分布

同樣方法可以得出多機器人在協作空間內的可操作度分布情況，圖6給出了z=0.69m的平面上3個機器人協作時的可操作度MMR的分布情況，其中右側的豎條表征了不同顏色所代表的可操作度值，由圖6中可以看出，在黑色區域可操作度趨近于0，此時由于某個機器人接近或處于奇異位形，導致協作系統靈活性最差，而灰白色區域可操作度較大，協作系統靈活性較好。

圖6 z=0.69m 平面下多機器人可操作度分布

對多機器人系統的協作空間的整體可操作度進行計算并歸一化處理，得到協作空間內系統的靈活性表達剖視圖，在MATLAB中可視化表達出來，如圖7所示。圖7中，用多種顏色分別表示多機器人協作時的靈活性程度，系統的靈活性范圍在[0,0.2)的區域用藍色表示；系統的靈活性范圍在[0.2,0.4)的區域用青色表示；系統的靈活性范圍在[0.4,0.6)的區域用綠色表示；系統的靈活性范圍在[0.6,0.8)的區域用黃色表示；系統的靈活性范圍在[0.8,1]的區域用紅色表示。從圖中可以得到多機器人協作的系統靈活性的分布規律。

圖7 協作空間靈活性剖視圖

由多機器人協作系統在協作空間中的靈活性分布情況可知，工作范圍在（x、y、z單位為m）x∈[?0.1,0.1]，y∈[0.15,0.35]，z∈[0.55,0.75]區域的多機器人協作靈活性較高，因此，在進行運動規劃時，應當盡量保證工作區域在x∈[?0.1,0.1]，y∈[0.15,0.35]，z∈[0.55,0.75]的范圍內。而靠近協作空間邊界的部分無法實現多機器人協作，機器人運動靈活性最差。分析可知，點C0(0,0.25,0.6)位于靈活性較高區域的中心點，因此，將該點作為最優初始焊接位置點，搬運機器人搬運工件到協作空間內，并將工件坐標系原點與該點重合，然后配合焊接機器人進行焊接任務，如此可以保證工件上的焊縫點均處于靈活性較高的區域，從而確保多機器人協作系統在焊接過程中的運動靈活性。

4 結語

本文以多機器人協作系統為研究對象，通過蒙特卡羅法得到多機器人協作空間，采用可操作度作為靈活性指標，建立了一種用于多機器人協作系統的靈活性評價模型，并使用MATLAB進行仿真將系統的靈活性可視化，從而選取機器人合適的操作空間。在本文選取的靈活性高的空間工作的基礎下，為后續多機器人的軌跡規劃做好鋪墊。