齒面硬化層對重載齒輪力學性能的影響研究

沈益晨 陳啟東

（①蘇州大學機電工程學院，江蘇 蘇州 215000；②常熟理工學院機械工程學院，江蘇 常熟 215500）

重載齒輪是傳遞運動和動力的傳動系統核心關鍵零件，在礦山機械、航空航天和新能源等行業有著廣泛的應用，因此，對其服役性能和疲勞壽命也提出了很高甚至是苛刻的要求。在齒輪的生產過程中，經常會通過滲碳、滲氮、噴丸以及涂敷涂層等工藝對齒輪進行表面硬化處理來提高整體性能，延長使用壽命。王克勝[1]等從有效硬化層深度的定義出發，得出了有效硬化層深度的最小值和最大值分別由接觸強度和彎曲強度決定的結論。豐瑞華[2]等建立了漸開線齒輪進行激光淬火時的三維溫度場數值模型并進行模擬，獲得了與試驗一致的結果。郁俐[3]等研究了強力噴丸對18CrNiMo7-6鋼不同硬化層深度齒輪性能的影響。Tobie T[4]等研究了滲碳深度對滲碳齒輪點蝕強度和彎曲強度的影響，得出在不同工作條件下的最佳滲碳深度。Moorthy V[5]等評估不同涂層下斜齒輪的性能，研究認為，Nb-S涂層齒輪的整體接觸疲勞性能最好。Karthick S[6]等研究了通過使用噴丸強化工藝來提高 SAE9310錐齒輪的機械和表面性能，以獲得所需的性能特征和對表面層特征的最大影響因素。

可見，國內外學者對齒輪表面硬化技術已經做了很多研究，然而，這些研究大多集中在工藝參數對表面硬化結果產生的影響。對于齒面硬化層中硬度的梯度分布研究較少，傳統的計算方法無法準確地得到齒輪在不同硬化深度下的應力分布及變化規律。本文利用多層均質層代替硬化部分，以某型號采煤機重載齒輪為對象，建立更切合實際的硬化齒輪有限元模型，考慮不同的硬度梯度分布、不同的硬化層厚度下齒輪產生的應力分布，研究齒面硬化層對重載齒輪力學性能的影響，對準確分析表面硬化齒輪的強度及表面加強工藝具有重要的理論和指導意義。

1 模型建立及驗證

1.1 赫茲接觸基本理論

齒輪接觸強度問題普遍以赫茲接觸理論作為理論基礎。兩個圓柱體的軸線相互平行，其彈性模量分別為E1、E2，泊松比分別為μ1、μ2，半徑分別為r1、r2，由單位長度上的力F壓緊，此時，在平行于軸線，寬度為 2a的區域形成接觸，由于圓柱體長度為單位長度，模型可簡化為二維接觸模型，如圖1所示。根據赫茲接觸理論可知最大接觸應力P，其表達式為

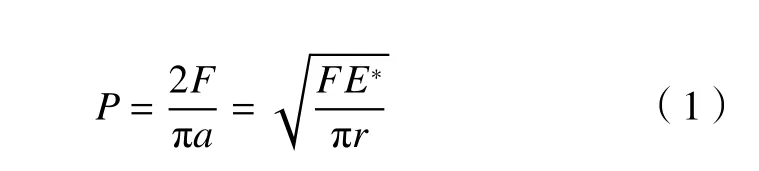
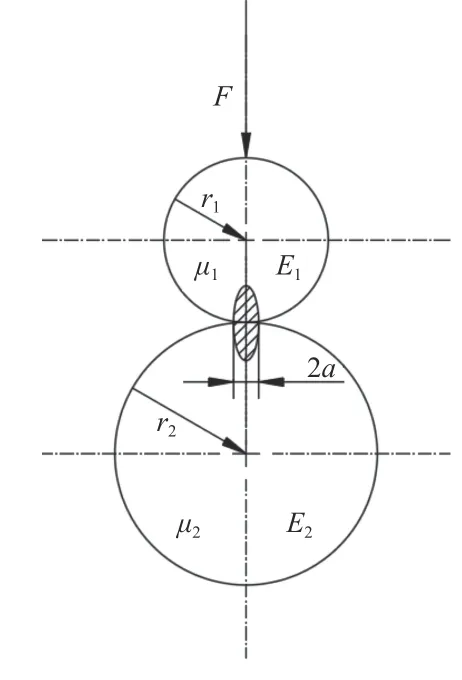
圖1 赫茲接觸模型

式中：a為接觸半徑，；E?為等效彈性模量，；r為綜合曲率半徑，。

最大剪應力τ為：

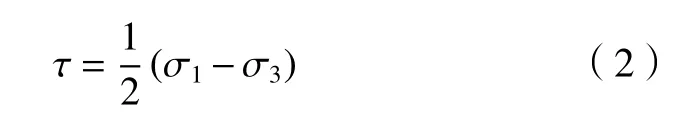
式中：σ1、σ3分別為主應力的最大值和最小值。

1.2 硬化層模型建立方法

齒輪硬度梯度的合理建模是本研究的關鍵，建立準確的硬化層模型對于問題的分析與研究才有實際意義。因此，本研究提出一種用多層均質層來替代齒輪硬化層的建模方法，利用雙三次B樣條曲面理論[7]獲得齒廓曲面，以該齒廓面為基面，沿點陣的負法向方向進行等距偏置，再以等距偏移面為基礎向內偏移，以此往復，得到組成齒輪硬化部分的各均質層。

圓柱齒輪的齒廓由漸開線曲線、齒根過渡曲線、齒頂圓弧和齒根圓弧組成。漸開線曲線方程為

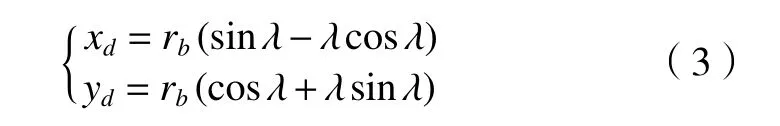
式中：xd、yd分別為曲線上點的橫、縱坐標；rb為基圓半徑；λ=tanα，α為壓力角。

齒根過渡曲線是在齒輪加工過程中由刀尖的圓角形成的。加工刀具和加工方法可以改變齒根過渡曲線。本研究采用滾齒法加工的齒輪，齒根過渡曲線是漸開線延伸的等距曲線。齒根過渡曲線的參數方程為

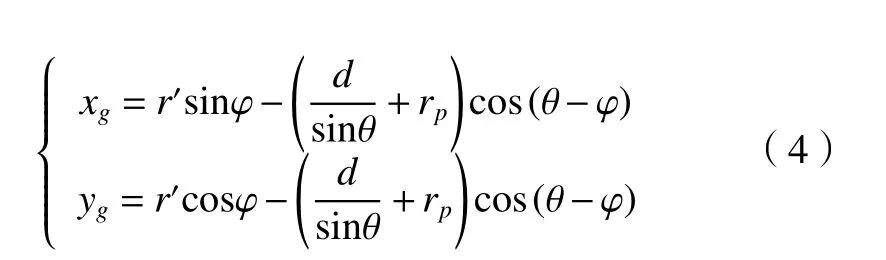
齒頂圓弧與齒根圓弧的方程分別為

即齒頂圓弧與齒根圓弧橫坐標分別等于齒頂與齒根圓弧半徑。

通過齒廓曲線方程可以獲得一系列的齒廓點，根據曲率大小自適應調整齒廓上取點的密度，以保證造型的精度。在完全獲得齒廓點后，沿軸線方向陣列若干層，得到齒廓面的點矩陣Ai, j。雙三次B樣條曲線方程為

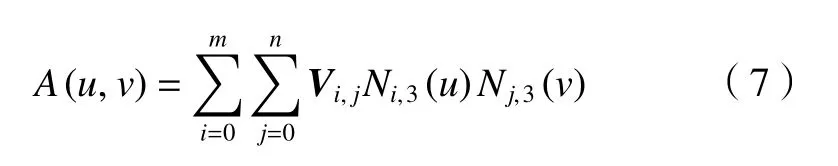
式中：Vi, j（i=0,1,···,m；j=0,1,···,n）為曲面控制點矩陣；Ni,3（u）和Nj,3（v）分別為分別為沿u和v方向的3次B樣條基函數。

通過式（6）可以計算出曲面上每一點u和v方向的切向量。每一點上的法向量是兩個切向量的叉積，再除以交叉模的大小得到單位法向量n。將該點沿單位法向量反向偏移ti距離即可得到該點的法向偏移點，表達式如下。

將齒廓點陣沿法線方向偏移t1距離，得到偏移點陣并進行擬合，得到第一個等距偏移曲面，該曲面與齒廓曲面順次連接形成第一層硬化層。以第一個偏移曲面為基面，繼續向內建立等距偏移曲，形成第二層均質硬化層，重復上述操作，最終可以得到其余硬化層。

1.3 齒輪有限元建模及驗證

以某采煤機減速器一對漸開線直齒輪為研究對象，其相關參數如表1所示。通過上述方法獲取齒廓線的點矩陣，并根據點的坐標序列生成igs文件。然后，將文件導入通用建模軟件，通過擬合點矩陣得到齒廓面。利用外部編程成功地得到了等距偏移曲面。將生成的等距偏移曲面的igs文件導入到ABAQUS中，利用由面生成體的命令得到硬化層實體模型。最后通過陣列以及布爾運算等操作構建出齒輪模型。

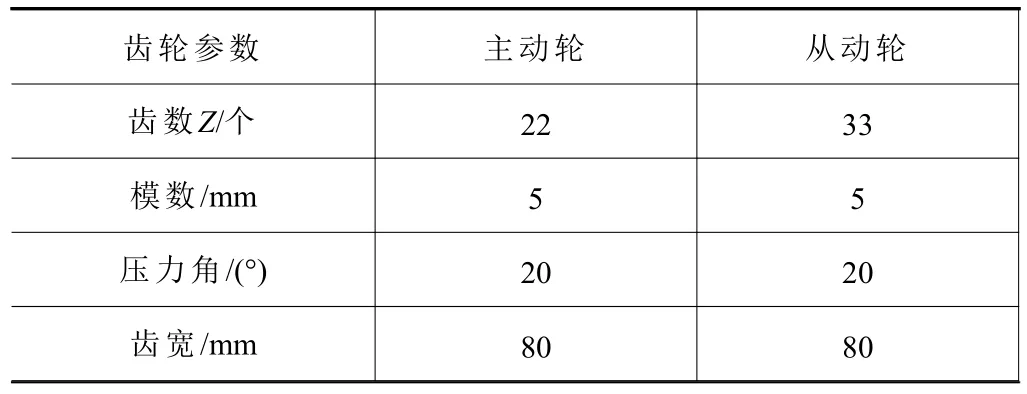
表1 減速器齒輪參數

考慮到齒輪是高度對稱部件，因此為節省計算量及時間，取1/4進行分析，圖2所示為將硬化層分為3層的主動輪。齒輪基體材料選取采煤機齒輪常用的17CrNiMo6[8]，彈性模量E=210 000 MPa，泊松比υ=0.3；最外層彈性模量E'=220 000 MPa，泊松比υ'=0.3。硬化層組元成分分布采用Wakashima K等[9]提出的冪函數形式漸變，沿齒輪徑向方向上分布為

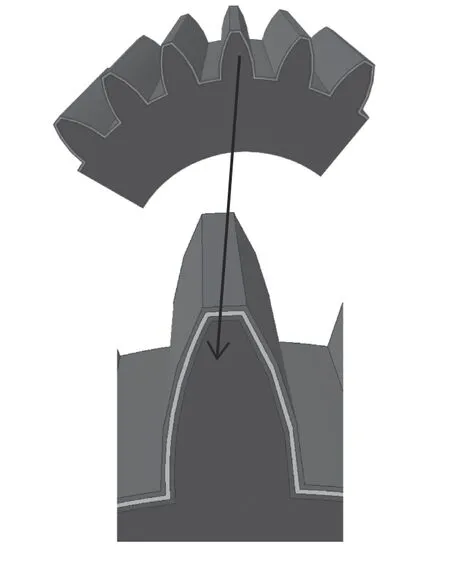
圖2 主動輪示意圖

式中：V(h)為最外層材料在硬化層中的體積分數；h為沿著齒輪厚度方向硬化層厚度；δ為硬化層的總厚度；p為成分分布指數；通過改變p值的大小，可以改變硬度梯度分布形式。

本算例網格類型為四邊形一階非協調單元，對主要受力的輪齒部分進行加密，如圖3所示；以小齒輪為主動輪，大齒輪為從動輪，首先將齒輪內圈與各自的中心進行耦合，然后對主動輪中心施加大小為16 000 N·m的轉矩，分別釋放主、從動輪繞軸線的旋轉自由度，約束住其余所有自由度，如圖4所示。由于齒輪在嚙合過程中表面既存在滾動又存在滑動[10]，此接觸類型設置為Frictional，摩擦系數設置為0.1。

圖3 齒輪網格模型

圖4 齒輪裝配圖

將模型提交運算，選取一對輪齒具有代表性的6個增量步為例，計算結果如圖5所示。由應力云圖可知，齒輪嚙合過程中，應力分布以接觸點為中心，呈現均勻散射狀，輪齒的齒頂、齒根及接觸齒面所受應力較大，且接觸點中心處產生最大接觸應力，其中最大接觸應力為952 MPa。由式（1）計算可得赫茲接觸理論強度為927 MPa，有限元計算結果與理論公式計算結果相比，誤差小于3%，這表明有限元模型計算精度高，能夠準確模擬后續不同硬化層齒輪的應力場分析。

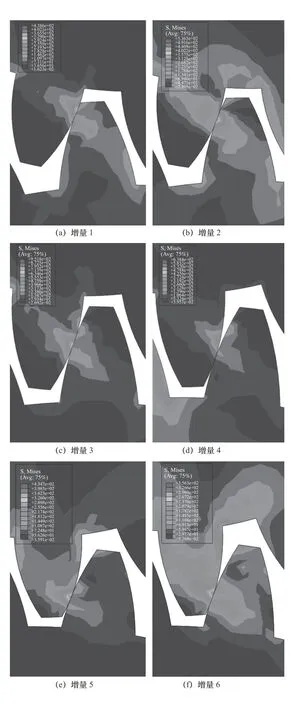
圖5 應力云圖

2 力學性能分析

2.1 有無硬化層對應力的影響

傳統的齒輪應力分析，將硬化層視作與基體相一致的材料，本文提取嚙合線上均勻分布的10個接觸點作為研究對象，近似得到單個輪齒在一個嚙合周期內的接觸應力變化規律，比較兩種建模方法的應力大小。圖6為有無硬化層的接觸應力情況。由圖可知，兩種模擬方法的接觸應力發展趨勢相似，嚙合過程中接觸應力值先呈現上升趨勢，然后在接觸點5和6之間應力達到峰值，最后應力值逐漸減小。在對硬化層進行分層處理后，接觸應力值整體有所下降，并且應力值變化整體趨于平緩，在接觸中心附近，應力峰值從1 013 MPa降低到952 MPa。通過與理論計算值比較，有限元仿真的結果整體大于理論值，這是因為理論計算只考慮對稱循環應力最大值作為最大應力值，忽略了脈動循環應力，而利用有限元方法讀取結果時，根據的是第三強度理論，讀取表面最大應力。同時，設置硬化層的計算值更接近理論值，說明該建模方法更接近實際，具有一定科學性。

圖6 有無硬化層接觸應力對比

2.2 硬化層硬度梯度形式對應力的影響

建立2 mm厚的硬化層，依次改變硬化梯度分布形式指數p，研究不同硬化層梯度形式對齒輪應力場的影響。圖7所示為不同硬度梯度下的最大接觸應力值及產生位置。由圖可知，最大接觸應力值隨著硬化層分布指數的增大逐漸減小，減小趨勢趨于平緩，表明硬化層分布指數對最大接觸應力值的影響越來越小；當分布指數p小于1時，最大接觸應力發生位置變化不大，發生在表層，隨著硬化層分布指數增大，最大接觸應力位置迅速下移，當p=4時，最大接觸應力已經離開硬化層進入基體。

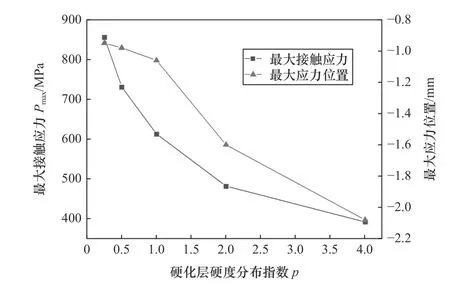
圖7 硬化層分布指數對接觸應力的影響

圖8為硬化層分布對剪應力分布的影響，橫坐標l/a表示與接觸點的距離。由圖可知，剪切應力隨著l/a的增大而增大，最大值出現在接觸半寬附近；在l/a=1附近剪切應力有一個突變，隨后逐漸減小。剪切應力隨硬化層分布指數的增加有所變化，且變化影響較大。當分布指數p為0.25～1時，接觸半寬附近的剪切應力逐漸減小，當分布指數p為1～4時，接觸半寬附近的剪切應力又開始增大。

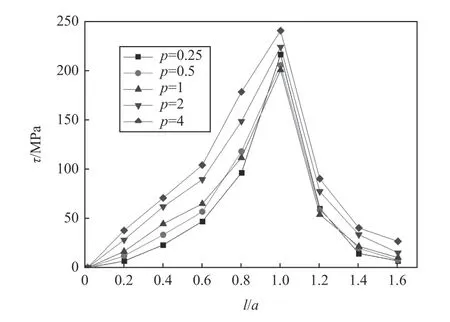
圖8 硬化層分布指數對剪切應力的影響

2.3 硬化層厚度對應力的影響

將模型硬化層層厚度依次設置為0.5 mm、1 mm、1.5 mm、2 mm，研究不同硬化層厚度對齒輪應力場的影響。圖9所示為不同厚度下的最大接觸應力值及產生位置。由圖可知，不同厚度的硬化層對接觸應力影響較大，隨著硬化層厚度增加，最大接觸應力先減小后增大，硬化層厚度為1 mm時，接觸應力最小。硬化層厚度過小或過大時，均產生較大接觸應力且變化幅度陡峭；隨著硬化層厚度增加，最大接觸應力發生位置開始下移，與齒面距離逐漸增大，當硬化層厚度在0.6 mm左右時，最大接觸應力進入到硬化層，當厚度達到1.5時，最大接觸應力位置開始迅速向齒根方向移動。

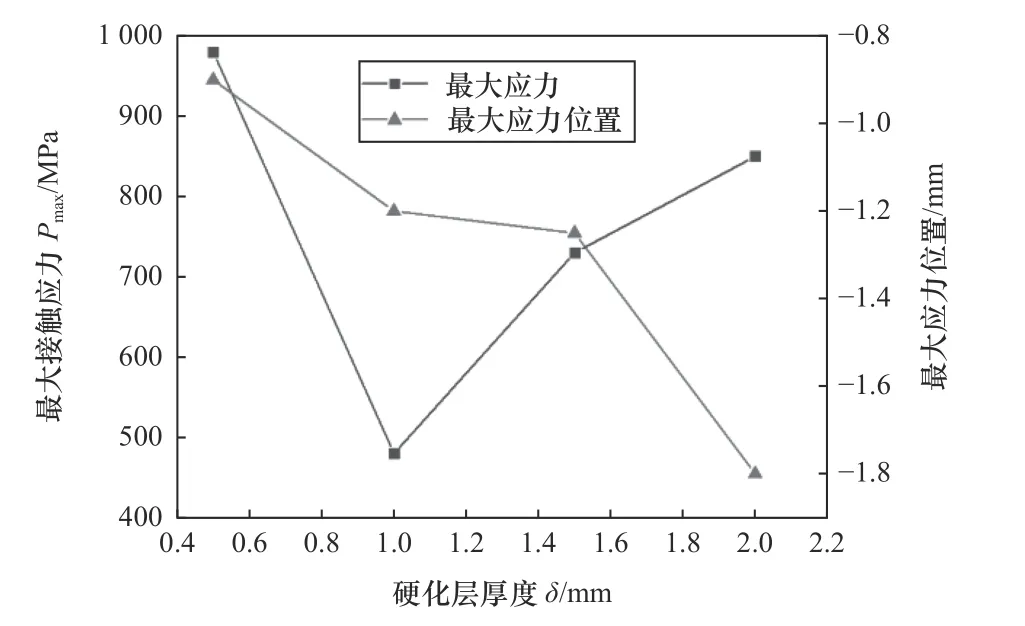
圖9 硬化層厚度對接觸應力的影響

圖10為硬化層厚度對剪應力分布的影響。由圖可知，最大剪應力出現在l/a=1處，即接觸半寬的位置并且隨后迅速減小直至趨于零；隨著硬化層厚度增加，剪應力明顯減小且變化更加平緩，表明硬化層厚度對界面影響較大，厚度的適當提高可以緩解齒面磨損剝落。

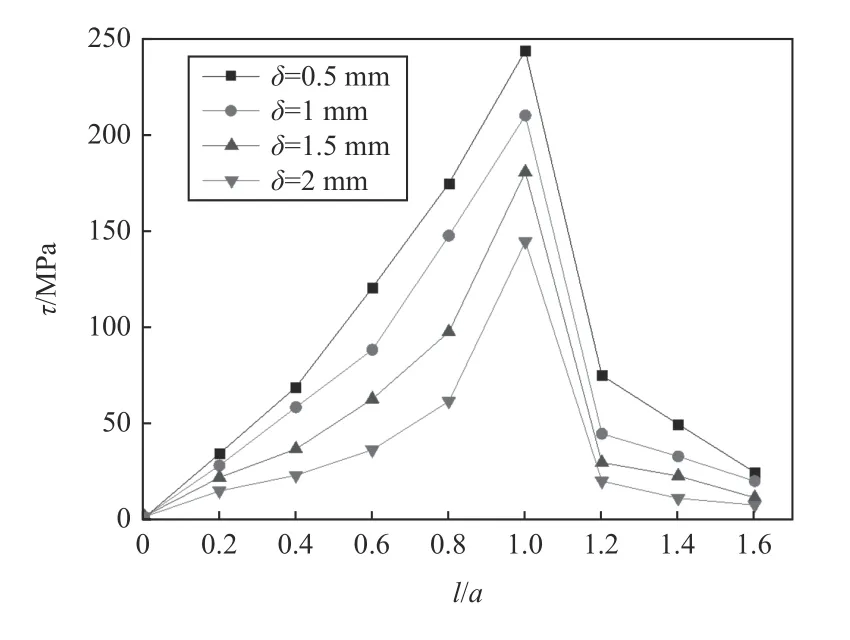
圖10 硬化層厚度對剪切應力的影響

3 結語

通過建立某型號含梯度硬化層齒輪的有限元模型，對采煤機重載工況下齒輪的受力情況進行分析，探究了硬化層梯度分布形式、硬化層厚度等因素對采煤機重載齒輪力學性能的影響，得到以下結論：

（1）本文提出的表面硬化齒輪建模方法對其進行嚙合性能仿真結果更加接近于實際情況，具有一定的科學性。

（2）硬化層分布指數的增大能有效減小接觸應力，分布指數過大，最大接觸應力將發生在齒輪基體，分布指數p=1時，剪切應力最小，提高了齒輪使用性能，延長使用壽命。

（3）硬化層厚度對最大接觸應力影響較大，剪切應力隨硬化層厚度的增加而增大。綜合考慮應力及界面結合強度，硬化層厚度應當控制在1～1.5 mm。