協(xié)作干擾時頻同步誤差對安全通信性能影響

肖尚輝，陳燕銘，王梓豫，郭文博，邵士海

(1.電子科技大學 通信抗干擾技術國家級重點實驗室，四川 成都 611731；2.成都工業(yè)學院 電子工程學院，四川 成都 610031)

隨著無線通信技術的蓬勃發(fā)展，無線通信安全問題引起人們的廣泛關注。為了實現(xiàn)可靠保密通信，現(xiàn)有設備常采用基于網絡層密鑰加密的信息安全技術。然而量子計算機的出現(xiàn)，使得現(xiàn)有解密算力呈指數(shù)級提升，給傳統(tǒng)網絡層加密技術帶來了嚴峻的挑戰(zhàn)[1]。物理層安全技術作為更有效、更具應用潛力的新安全技術應運而生，其核心是利用無線信道的廣播特性和疊加特性，實現(xiàn)無線介質上信息可靠傳輸，且無須借助加密密鑰。由于物理層安全技術與網絡層加密技術相互獨立，可以借助物理層安全技術來增強現(xiàn)有的網絡層安全措施，從多個維度提高無線通信的安全性[2]。

協(xié)作干擾是實現(xiàn)物理層安全通信的重要手段，其核心思想是通過增添協(xié)作干擾信號來降低非授權竊聽用戶的信噪比，以提高系統(tǒng)通信安全性[3-4]。如圖1所示，竊聽節(jié)點E在獲取來自發(fā)送節(jié)點S的信號同時，收到來自協(xié)作干擾節(jié)點J的干擾信號影響，惡化了接收信噪比。接收節(jié)點R也會接收到協(xié)作干擾信號，但利用協(xié)作干擾信號的先驗信息，R可以消除協(xié)作干擾影響[5]。

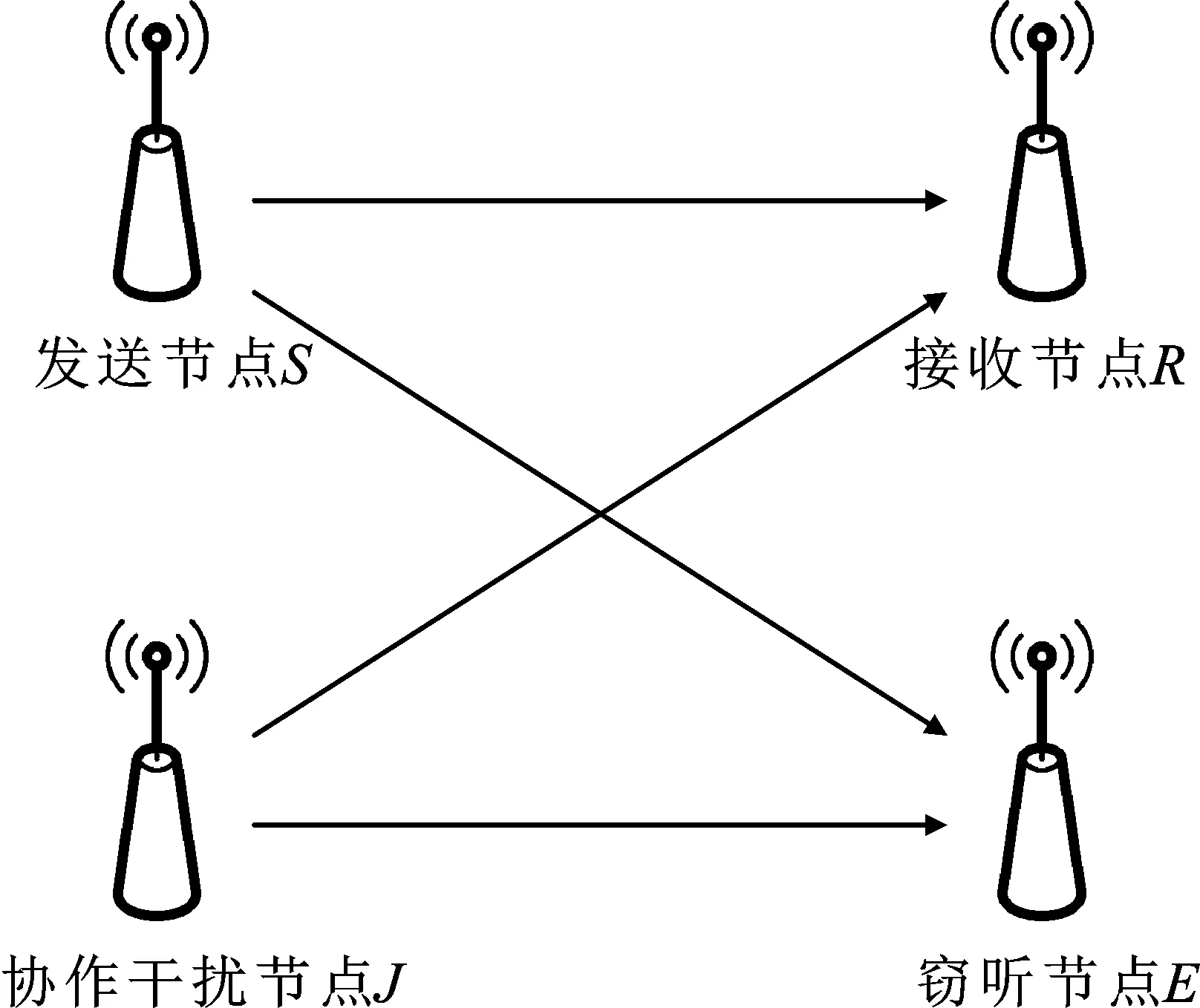
圖1 協(xié)作干擾下安全通信示意圖

目前研究人員對物理層協(xié)作干擾技術進行了相關探究。文獻[6]設計了一種全雙工干擾中繼方案，竊聽用戶同時從源節(jié)點和中繼節(jié)點接收相互干擾信號，有效地降低了竊聽容量，從而提升了系統(tǒng)的保密性能。文獻[7]考慮到傳統(tǒng)協(xié)作干擾持續(xù)發(fā)送干擾信號帶來的能量浪費和過度干擾問題，設計了一種間歇性干擾策略，實現(xiàn)了聯(lián)合安全需求和干擾功率優(yōu)化的目標。文獻[8]采用反向傳播神經網絡對信道估計誤差進行模擬和計算，并推導了最大保密率下信息偵聽信號和人工噪聲信號之間的最佳功率分配比。文獻[9]針對協(xié)作干擾通信中的頻率偏移和功率放大器非線性失真，提出了一種非線性自干擾消除方案，擴展了發(fā)射功率范圍以提供更好的安全通信性能。

在授權接收機對協(xié)作干擾進行精準重建和對消是實現(xiàn)安全通信的前提，但現(xiàn)有研究工作均假定協(xié)作干擾在理想時間和頻率同步下實現(xiàn)完美對消。由于硬件和傳播環(huán)境的影響，且受實際工程時頻同步精度的制約，盡管可以通過優(yōu)化時頻同步算法來降低同步誤差，但始終存在殘余誤差，理想時間和頻率同步是不可實現(xiàn)的[10-11]。針對這一問題，筆者研究了協(xié)作干擾時頻同步誤差對安全通信性能的影響，為設計實用安全通信系統(tǒng)提供理論支持。

針對上述問題，基于高斯竊聽信道模型，筆者從理論上分析了協(xié)作干擾信號時頻同步誤差對授權用戶安全通信性能的影響，并進行了仿真驗證。首先，在高斯竊聽信道模型下，得到了干擾抑制后的殘余干擾功率表達式；然后推導了干擾抑制比、解調誤碼率、保密容量的閉合表達式；最后進行了計算機仿真驗證。

1 系統(tǒng)模型

筆者采用的協(xié)作干擾抑制模型如圖2所示。該模型包括發(fā)送節(jié)點、協(xié)作干擾節(jié)點和接收節(jié)點，每個節(jié)點都配備單天線。發(fā)送節(jié)點和協(xié)作干擾節(jié)點的比特流通過調制、數(shù)模轉換和射頻處理后經天線發(fā)射，接收節(jié)點收到期望信號和干擾信號的疊加信號，經過下變頻、模數(shù)轉換和干擾抑制后，解調得到期望信號的估計值。

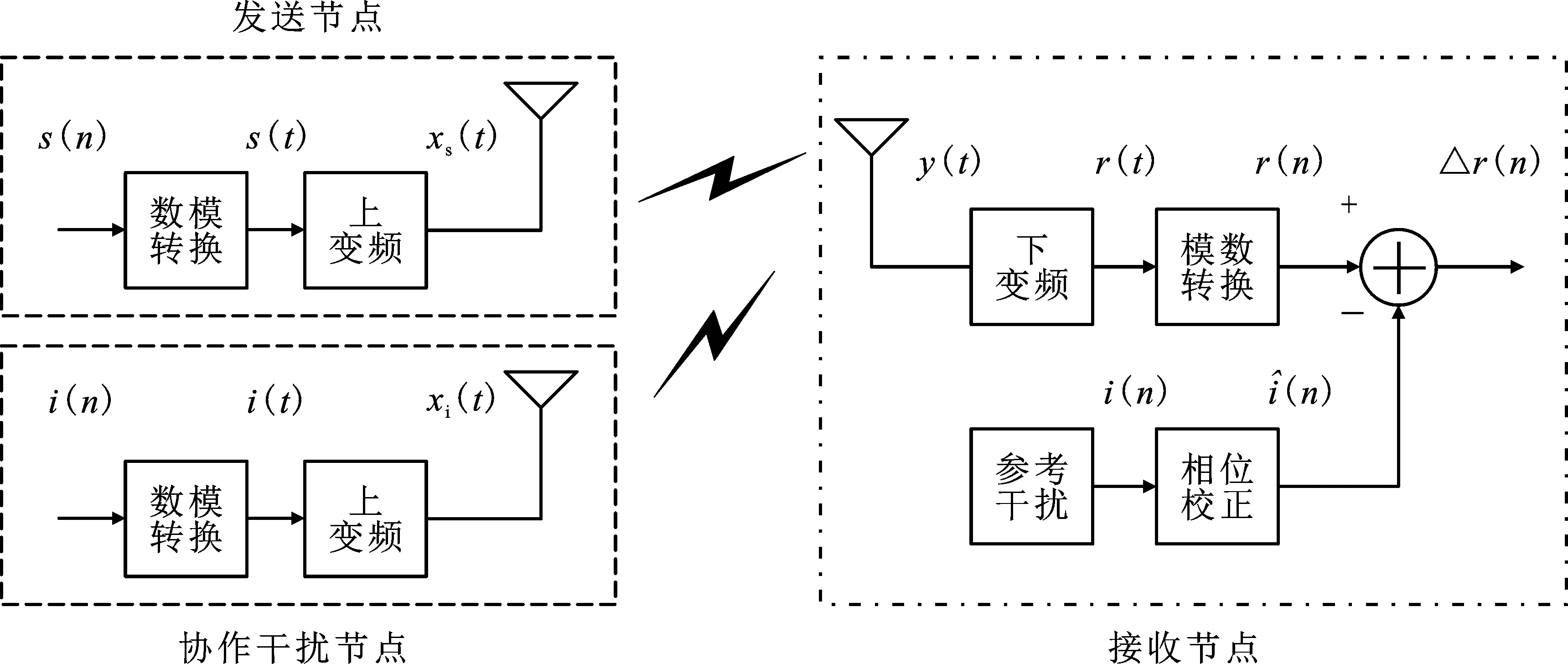
圖2 協(xié)作干擾抑制示意圖

1.1 發(fā)送節(jié)點模型

首先考慮發(fā)送節(jié)點。假設發(fā)送節(jié)點的基帶離散信號為s(n)∈{0，1}，經過數(shù)模轉換后，變?yōu)榛鶐нB續(xù)信號，記作s(t)。s(t)經過上變頻后由射頻天線發(fā)射出去，發(fā)射信號可以表示為

xs(t)=(Ps)1/2s(t)exp(j(2πfst+φs)) ，

(1)

其中，Ps是發(fā)送節(jié)點發(fā)射信號的功率，fs是通信信號的載波頻率，φs為通信信號載波的初始相位。

1.2 協(xié)作干擾節(jié)點模型

類似地，定義協(xié)作干擾節(jié)點的基帶離散信號為i(n)，經過數(shù)模轉換后，變?yōu)榛鶐нB續(xù)信號i(t)。i(t)上變頻后通過射頻天線發(fā)射出去，發(fā)射信號可以表示為

xi(t)=(Pi)1/2i(t)exp(j(2πfit+φi)) ，

(2)

其中，Pi是協(xié)作干擾節(jié)點發(fā)射信號的功率，fi是協(xié)作干擾信號的載波頻率，φi為協(xié)作干擾信號載波的初始相位。

1.3 信道模型

假設通信信號和協(xié)作干擾信號都經歷加性高斯白噪聲(Additive White Gaussian Noise，AWGN)信道，經過無線信道傳輸，接收節(jié)點接收到的射頻信號為[12]

y(t)=Asxs(t-ts)+Aixi(t-ti)+n(t) ，

(3)

其中，As和Ai分別是通信信號和協(xié)作干擾信號經歷的信道衰減因子，不失一般性，假設為1[13]；ts為通信信號的傳輸時延；ti為干擾信號的傳輸時延；n(t)是均值為零、方差為σ2的加性高斯白噪聲。

1.4 接收機模型

經過下變頻后，基帶接收信號為

r(t)=y(t)exp(-j(2πfr+φr))=(Ps)1/2s(t-ts)exp(j(2πΔfst+Δφs))+

(Pi)1/2i(t-ti)exp(j(2πΔfit+Δφi))+w(t) ，

(4)

其中，fr是接收節(jié)點的載波頻率；φr為載波的初始相位；Δfs=fs-fr和Δφs=φs-φr分別是通信信號收發(fā)端的載波頻率偏移和初始相位誤差；Δfi=fi-fr和Δφi=φi-φr分別是協(xié)作干擾信號收發(fā)端的載波頻率偏移和初始相位誤差；w(t)=n(t)exp(-j(2πfr+φr))，是等效基帶噪聲。

式(4)第1項記作rs(t)，為通信信號分量；第2項記作ri(t)，為干擾信號分量，則接收信號重新表達為

r(t)=rs(t)+ri(t)+w(t) 。

(5)

以1/Ts的采樣率進行采樣，對接收信號做模數(shù)轉換，得到基帶接收信號的離散形式：

r(n)=(Pi)1/2i(n-τ1)exp(j(2πεn+Δφi))+rs(n)+w(n) ，

(6)

其中，τ1=ti/Ts，為干擾信號歸一化時延；ε=ΔfiTs，為歸一化頻率同步誤差。式(6)第1項記作ri(n)，為干擾信號的離散形式；第2項和最后一項分別是離散化的通信信號和噪聲。

(7)

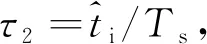
干擾抑制后的信號為

(8)

干擾抑制后的殘余干擾分量為

(9)

以下將研究歸一化時間同步誤差τ=|τ1-τ2|和歸一化頻率同步誤差ε對干擾抑制性能的影響。為了分析方便，假設通信信號和協(xié)作干擾信號相互獨立，且通信信號和協(xié)作干擾的載波初始相位均為0，即Δφs=Δφi=0。

2 性能指標分析

2.1 殘余干擾功率

式(9)得到了時頻同步誤差對殘余協(xié)作干擾信號影響的閉合表達式。下面將計算殘余干擾功率。不失一般性，設協(xié)作干擾信號為偽隨機序列[14]，則殘余干擾功率為

PΔ=E{Δ(n)Δ*(n)} ，

(10)

其中，(·)*表示取共軛。

將式(9)代入式(10)，得到

(11)

三角函數(shù)的求和公式[15]如下所示：

(12)

將式(12)代入式(11)，得到殘余干擾功率的閉合表達式為

(13)

其中，R(τ)是偽隨機序列的自相關函數(shù)。在接收機進行信號時間同步時，常見的時間同步算法可以將時間同步誤差控制在1個符號周期以內。因此，不考慮整數(shù)倍的同步時延誤差，重點研究小數(shù)時延的影響[16]：

i(n-τ)=τi(n-1)+(1-τ)i(n) 。

(14)

進行功率歸一化處理后，得

(15)

(16)

將式(16)代入式(13)，得

(17)

下面分別討論歸一化時延和頻偏對殘余干擾功率的影響。為了與后續(xù)仿真條件對應，取偽隨機序列長度N=1 023。

(1) 當歸一化頻偏為0時，式(17)退化為

(18)

特別地，當τ=0時，時頻完全同步，殘余干擾功率為0；當τ=0.63時，殘余干擾與抑制前干擾功率相同；當τ=1時，接收的干擾信號與重建干擾信號不相關，功率加倍。

(19)

(2) 當歸一化時延為0時，式(17)退化為

(20)

特別地，當ε=0時，時頻完全同步，殘余干擾功率為0；當ε=3×10-4時，殘余干擾與抑制前干擾功率相同；當ε=10-2時，接收的干擾信號與重建干擾信號不相關，功率加倍。

(21)

2.2 干擾抑制比

定義干擾抑制比(Jamming Cancellation Ratio，JCR)來度量無線通信系統(tǒng)對協(xié)作干擾信號的抑制程度[17]，用干擾抑制前后干擾加噪聲功率之比表示。干擾抑制比越大，系統(tǒng)對干擾信號的抑制效果越好。

(22)

從式(22)可以看出，干擾抑制比是關于殘余干擾功率的減函數(shù)。根據節(jié)2.1的結論可知：當τ=0，ε=0時，PΔ=0，干擾抑制比達到最大值：

(23)

其中，RJNR是干噪比；RJSR是干信比；RSNR是信噪比。

當τ和ε繼續(xù)增加時，干擾抑制比逐漸降低。特別地：當ε=0、τ=0.63或者τ=0、ε=3×10-4時，PΔ=Pi，干擾抑制比為0；當ε=0、τ=1或者τ=0、ε=10-2時，PΔ=2Pi，干擾抑制比為-3 dB。

2.3 解調誤碼率

考慮通信信號調制方式為正交相移鍵控(Quadrature Phase Shift Keying，QPSK)。接收端干擾抑制完成后，需要進行QPSK解調恢復原始比特流，解調誤碼率與解調器輸入信噪比γ有關。解調時，殘余干擾作為噪聲處理。QPSK解調器的輸入信噪比為

(24)

其中，Ps是通信信號功率，PΔ是干擾抑制后的殘余干擾功率。

高斯信道下QPSK的解調誤碼率為[18]

pQPSK=Q(γ1/2) 。

(25)

將式(24)代入式(25)，得到協(xié)作干擾信號存在時頻同步誤差時，授權用戶解調誤碼率為

(26)

2.4 保密容量

保密容量定義為最大可達保密速率。在加性高斯白噪聲竊聽信道中，保密容量定義如下[19]：

(27)

協(xié)作干擾抑制后，安全通信保密容量為

(28)

從式(28)可以看出，保密容量是關于殘余干擾功率的減函數(shù)。根據節(jié)2.1的結論可知：當τ=0，ε=0時，保密容量達到最大值，即

(29)

隨著τ和ε取值增大，保密容量逐漸降低。特別地，當ε=0、τ≥0.63或者τ=0、ε≥3×10-4時，保密容量為0，此時無法實現(xiàn)安全通信。

3 數(shù)值與仿真結果

為驗證協(xié)作干擾時頻同步誤差對干擾抑制比、解調誤碼率和保密容量這3個性能指標的影響，通過MATLAB仿真軟件，分別在不同信噪比和不同時頻同步誤差下進行實驗，仿真實驗參數(shù)如表1所示。取10 000幀數(shù)據統(tǒng)計平均后作為實驗結果。為方便對比，在表1所示仿真參數(shù)設置下，信噪比為10 dB時，由式(29)可得無時頻同步誤差時的系統(tǒng)保密容量最大值Cmax=1.662 bit/(s·Hz)。

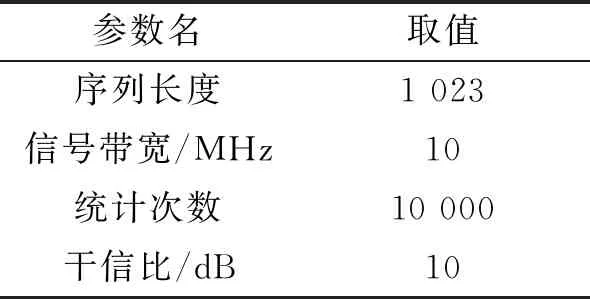
表1 仿真參數(shù)設置

3.1 時延誤差對干擾抑制比、誤碼率和保密容量的影響

圖3～圖5給出在歸一化頻偏為0，不同信噪比下，歸一化時延與干擾抑制比、誤碼率和保密容量之間的關系。仿真結果顯示，隨著時延增大，系統(tǒng)對協(xié)作干擾信號的抑制程度降低，干擾抑制比降低，保密容量降低，誤碼率增加。

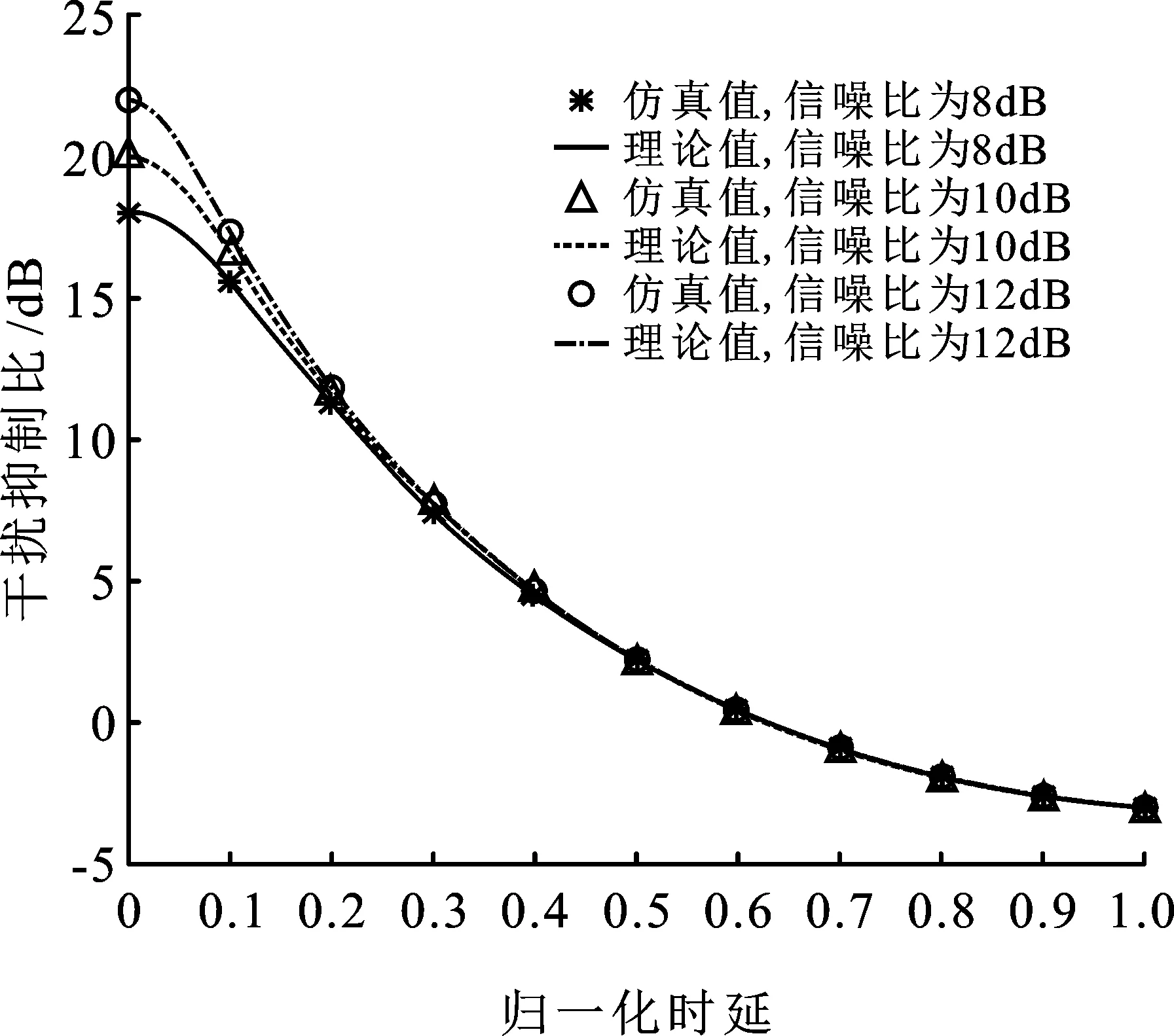
圖3 歸一化頻偏為0時，不同信噪比下歸一化時延與干擾抑制比關系示意圖

圖3顯示了時延對干抑制比的影響。以信噪比10 dB曲線為例，干擾抑制比隨著時延增大而降低。當歸一化時延為0.1時，干擾抑制比下降3.5 dB，約17.5%；當歸一化時延大于0.63時，干擾抑制比小于0 dB。這是因為接收信號的干擾分量與接收機重建的干擾信號疊加，使干擾信號功率增大。當歸一化時延為1時，干擾抑制比為-3 dB，接收干擾信號分量和重建干擾信號互不相關，因此功率加倍，系統(tǒng)的干擾抑制能力最差。

圖4顯示了時延對QPSK解調誤碼率的影響。隨著時延增大，誤碼率增加。當歸一化時延大于0.63時，不同信噪比的誤碼率曲線重合并趨于最大誤碼率，此時時延成為誤碼率的主要影響因素。

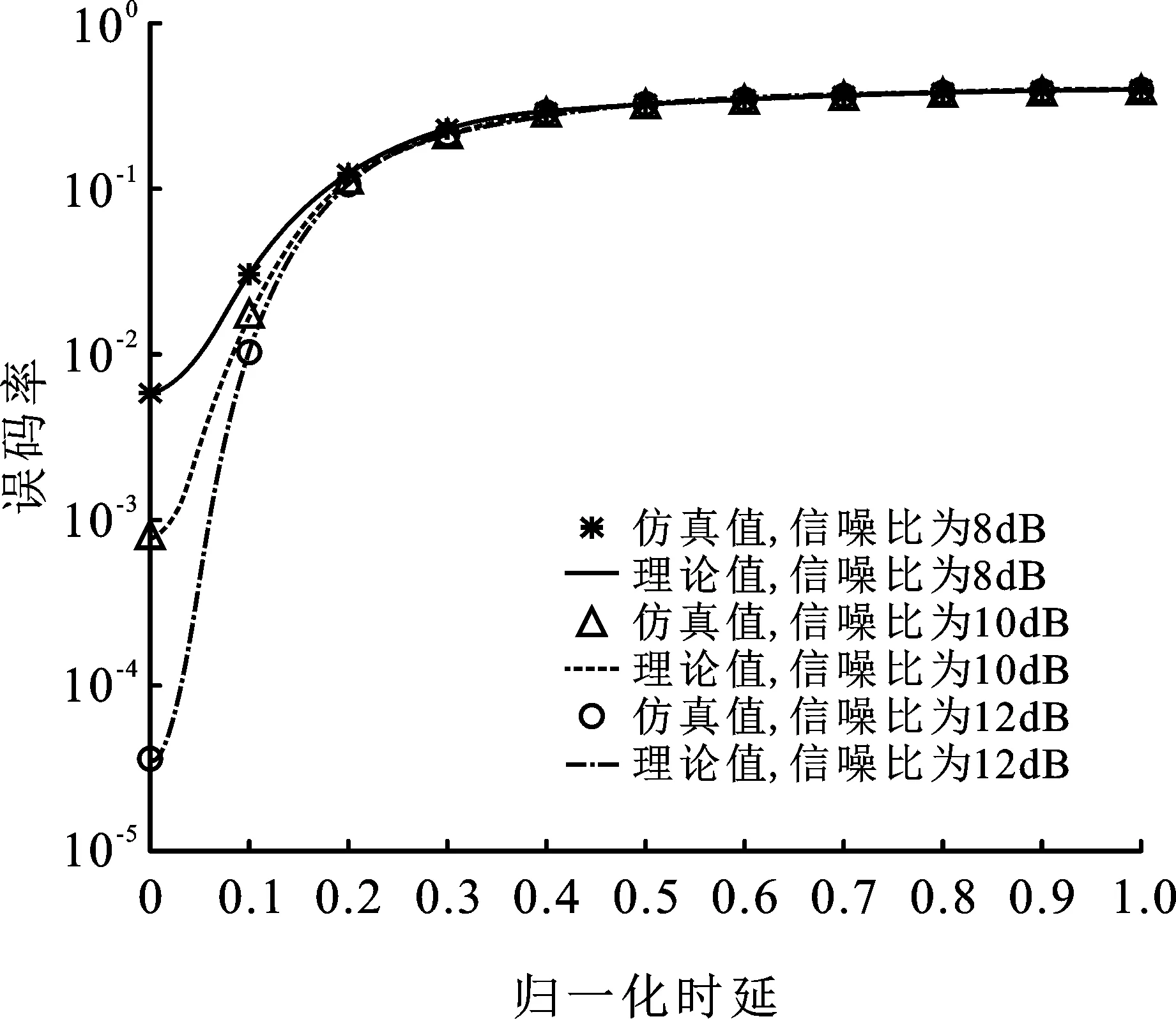
圖4 歸一化頻偏為0時，不同信噪比下歸一化時延與誤碼率關系示意圖

圖5顯示了時延對保密容量的影響。隨著時延增大，保密容量降低。以信噪比10 dB曲線為例，當歸一化時延為0.1時，保密容量下降0.5 bit/(s·Hz)，約30%；當歸一化時延大于0.63時，保密容量為0，主信道條件差于竊聽信道條件，此時無法實現(xiàn)安全通信。

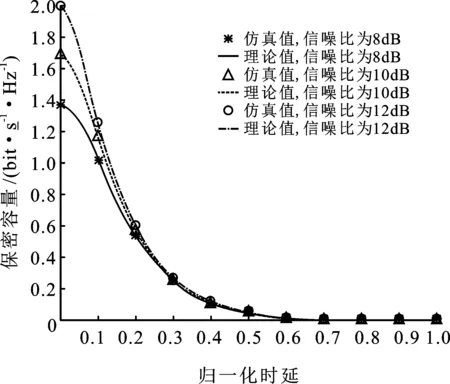
圖5 歸一化頻偏為0時，不同信噪比下歸一化時延與保密容量關系示意圖

3.2 頻偏對干擾抑制比、誤碼率和保密容量的影響

圖6～圖8顯示了頻偏對干抑制比、誤碼率和保密容量的影響。

圖6中，以信噪比10dB曲線為例，歸一化頻偏為10-5時，干擾抑制比下降0.6 dB，約3%；當歸一化頻偏大于3×10-4時，干擾抑制比小于0，接收信號干擾分量與重建干擾疊加使干擾信號功率增大；在歸一化頻偏達到10-2時，接收干擾分量和重建干擾信號互不相關，功率加倍，干擾抑制比為-3 dB。

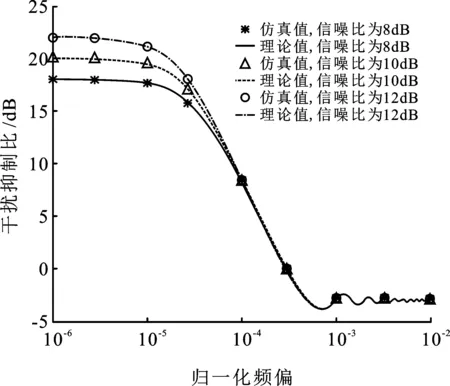
圖6 歸一化時延為0時，不同信噪比下歸一化頻偏與干擾抑制比關系示意圖

圖7給出歸一化時延為0時，不同信噪比下歸一化頻偏與QPSK解調誤碼率之間的關系。隨著頻偏增大，誤碼率提高。當歸一化頻偏大于3×10-4時，不同信噪比的誤碼率曲線重合并趨于最大誤碼率，此時頻偏成為誤碼率的主要影響因素。

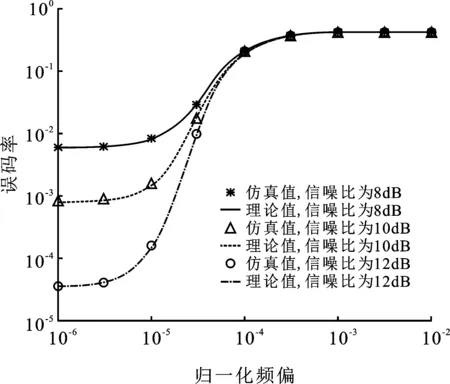
圖7 歸一化時延為0時，不同信噪比下歸一化頻偏與誤碼率關系示意圖

圖8給出歸一化時延為0時，不同信噪比下歸一化頻偏與保密容量之間的關系。隨著頻偏增大，保密容量降低，以信噪比10 dB曲線為例，歸一化頻偏為10-5時，保密容量下降0.1 bit/(s·Hz)，約6%；當歸一化頻偏大于3×10-4時，保密容量為0，主信道條件差于竊聽信道條件，此時無法實現(xiàn)安全通信。

圖8 歸一化時延為0時，不同信噪比下歸一化頻偏與保密容量關系示意圖

3.3 時頻同步誤差對干擾抑制比、誤碼率和保密容量的影響

圖9～圖11顯示了信噪比為10 dB下，存在時頻同步誤差對系統(tǒng)協(xié)作干擾信號的抑制性能影響的等高線。隨著時延或頻偏增大，系統(tǒng)對協(xié)作干擾信號的抑制程度降低，干擾抑制比和保密容量降低，誤碼率增加。

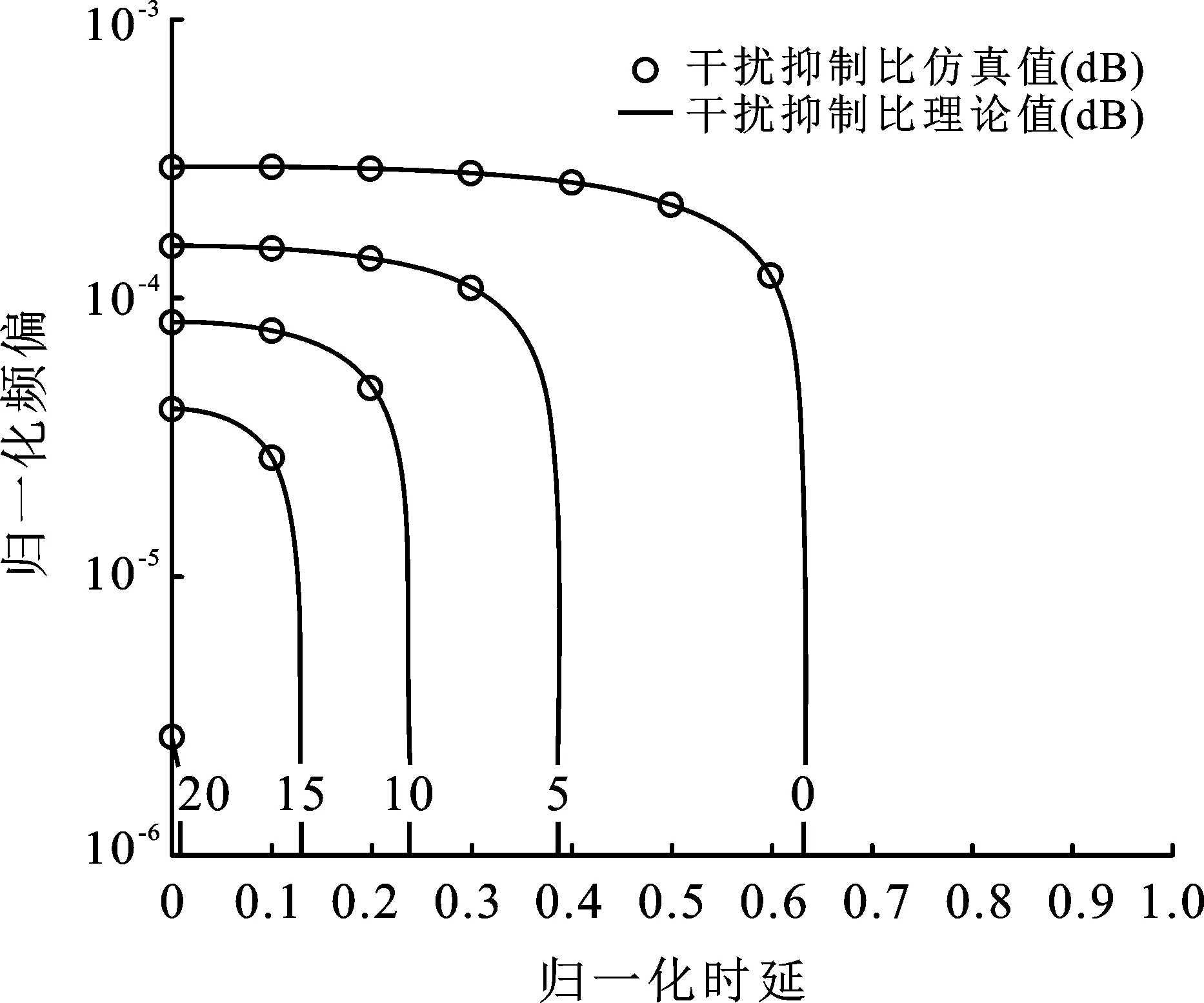
圖9 信噪比為10 dB，且存在時頻同步誤差時，干擾抑制比等高線示意圖

圖9給出了干擾抑制比等高線示意圖，當時頻同步誤差增大時，系統(tǒng)的干擾抑制比降低。當歸一化時延為0.24，頻偏小于10-4時，干擾抑制比保持為10 dB。

圖10顯示了解調誤碼率的等高線變化情況，隨著時延或頻偏增大，誤碼率升高。當歸一化時延為0.26，頻偏小于10-4時，誤碼率保持為0.2。

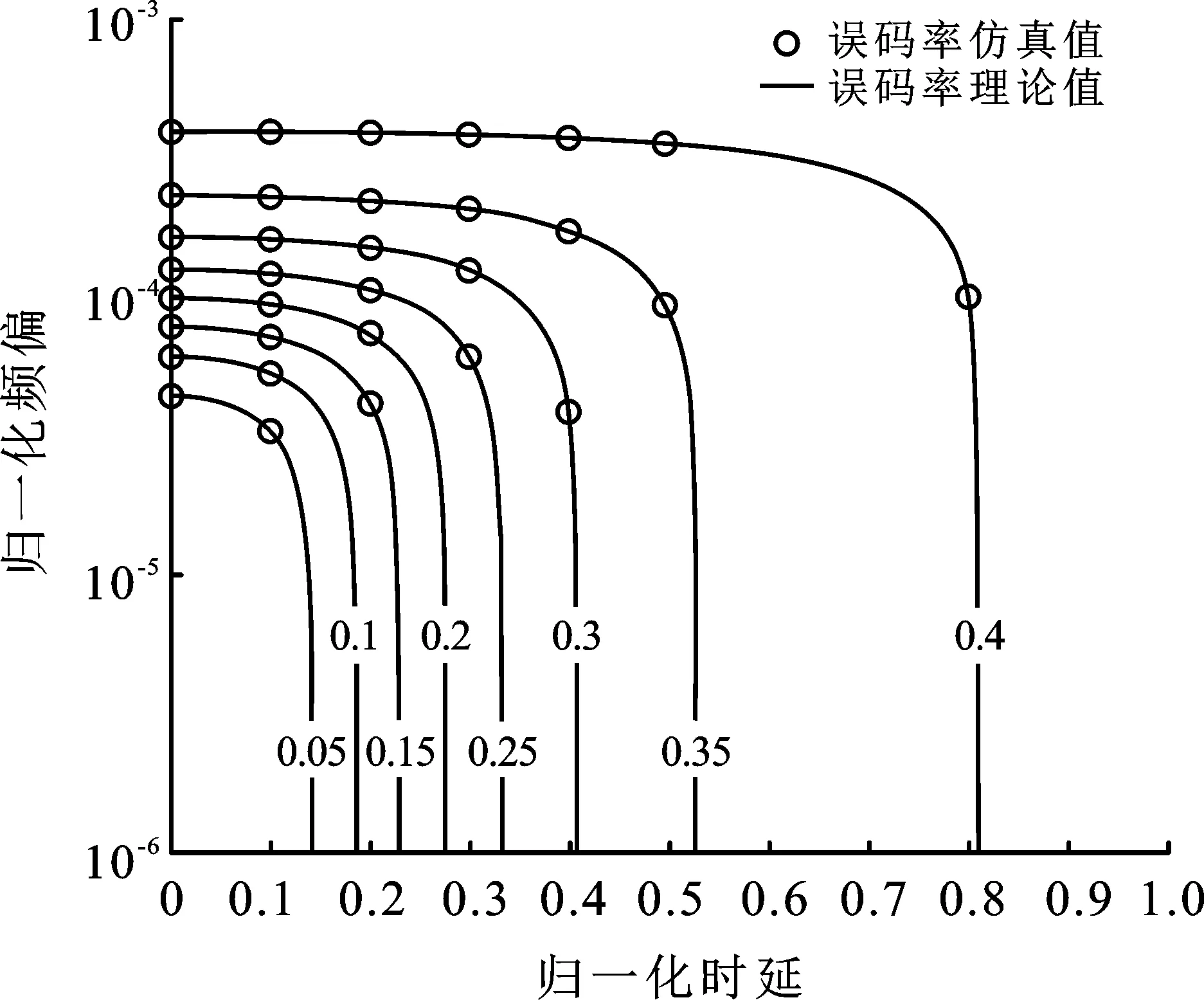
圖10 信噪比為10 dB且存在時頻同步 誤差時，誤碼率等高線示意圖

圖11給出了存在時頻同步誤差時，保密容量的等高線。當時頻同步誤差增大時，系統(tǒng)保密容量降低。當歸一化時延小于0.06且頻偏小于10-5時，保密容量損失小于16%；當歸一化時延為0.25且頻偏小于10-4時，保密容量保持為0.4 bit/(s·Hz)。為了使得保密容量大于0，應該滿足約束條件，即歸一化時延小于0.63且頻偏小于3×10-4。

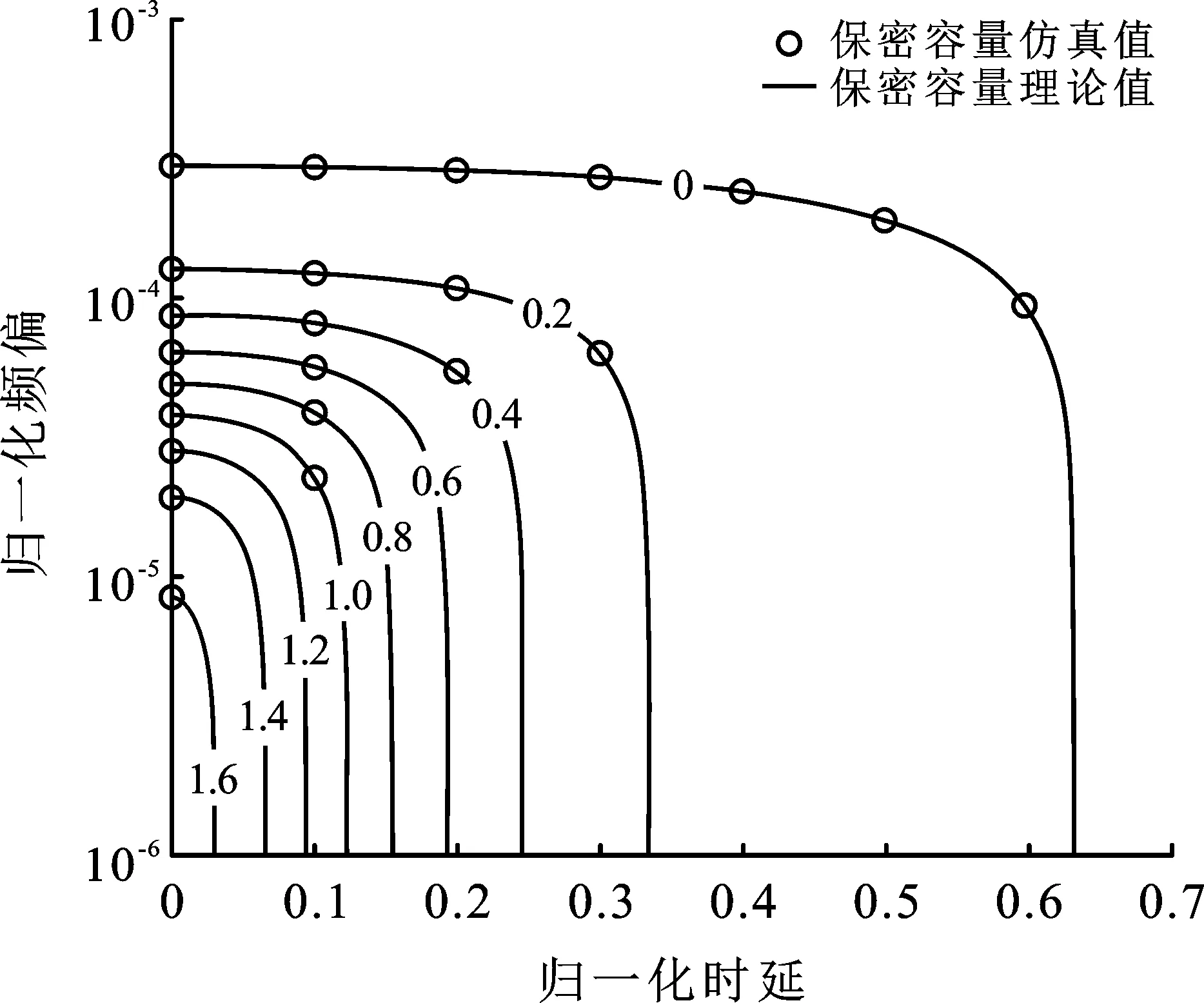
圖11 信噪比為10 dB且存在時頻同步 誤差時，保密容量等高線示意圖

4 結束語

筆者研究了高斯竊聽信道下，協(xié)作干擾時頻同步誤差對干擾抑制比、誤碼率和保密容量的影響，并根據殘余干擾信號功率推導出安全通信保密容量的閉合表達式。理論和仿真結果顯示，當歸一化時延小于0.06且頻偏小于10-5時，保密容量損失小于16%。當歸一化時延小于0.63且頻偏小于3×10-4時，保密容量大于0，可以實現(xiàn)安全通信。研究成果可為安全通信系統(tǒng)的設計提供理論支持和工程參考。