冰彎曲破壞的彈塑性近場動力學模型

張 媛，王 超，郭春雨，葉禮裕，劉 正

(哈爾濱工程大學 船舶工程學院，哈爾濱 150001)

近些年來，在氣候變暖、科學技術發展、經濟效益驅動以及一些政治和軍事領域的顯著價值需求下，極地航線開發、極地資源的勘探以及極地環境利用成為一種必然且迫切的趨勢[1]。這些變化極大地促進了更加頻繁的極地地區海洋結構物的作業活動，除此之外，多數內陸結冰水域仍舊常年進行各種海上作業活動。然而冰的存在能夠對結構物造成嚴重的損害，甚至造成結構物的破壞而無法正常作業。由此研究冰力學性能和破壞模式及其與結構物相互作用過程是支持極地以及冰區結構物發展的重要手段之一，而建立精確的冰本構模型是這其中的關鍵技術之一。

基于數值計算的冰力學特性、冰-結構物作用過程等研究近幾年快速發展：最初，學者們通常采用基于試驗獲得的經驗數據和數學物理分析的方法來計算冰的力學特性并且用于冰與結構物相互作用過程的冰載荷預報以及船舶運動性能預報[2-4]。然而上述文獻中對于海冰性質研究的方法，極大地依賴于經驗數據，不足以發展成完整成熟的數值模型[5]。后來，學者們紛紛采用基于傳統連續介質力學方法的數值手段來研究海冰的特性，例如有限元方法FEM[6-8]，改進有限元方法[9-10]，以及其他考慮冰細微參數的方法等[11]。然而傳統介質力學方法在處理大變形或者斷裂問題具有一定的局限性，不能準確地模擬冰破壞過程的裂紋擴展路徑。為了克服上述的科學問題，學者開始嘗試建立基于無網格方法的冰本構模型，這些方法里發展比較成型的有：離散元方法(Discrete element method,DEM)[12-13]，光滑粒子動力學(Smoothed particle hydrodynamics,SPH)[14-16]以及近場動力學方法(Peridynamics,PD)[17-19]等。其中DEM方法由于其顆粒狀的模型形式具有模擬浮碎冰和結構物碰撞、浮碎冰之間碰撞的優勢。而SPH和PD方法的粒子離散形式使其在海冰破碎以及裂紋擴展方面更具有更突出的優勢，不管是哪種粒子數值模型，雖然能夠處理斷裂問題，但是并不能完整精確地模擬冰力學性能和破壞特性，由此這些方法仍然處于發展前期，還需要投入大量的研究工作來建立適用于冰的準確數值模型。

近場動力學方法(PD)，是近二十年新興的一種非局部、無網格粒子、積分形式的計算方法，在斷裂問題域和非斷裂問題域上都可以連續求解[20]。該方法最早由Silling等[21-22]提出并建立推導了其控制方程，給出了基本的數值實現程序案例。PD方法主要兩種表現形式[21-23]，經推導和比較[24]兩種表達方式大同小異且具有相類似的計算精度。PD發展至今主要有鍵型、常規狀態型和非常規狀態型3種形式。且該方法已經成功應用于材料的彈性、塑性、熱力學等多種物理問題計算分析領域[25-27]。然而PD應用于冰計算領域剛剛起步，多數文獻采用基于鍵型的彈性模型來模擬冰的破壞特性，例如，冰與剛體柱的作用過程、冰槳作用過程等，忽略了泊松比的真實狀態和海冰具有塑性屈服過程的力學特性。由此本文主要的目的是建立基于狀態型PD方法的冰彈塑性本構模型，消除了鍵型對泊松比的限制，加入了冰破壞過程塑性變形過程，為后續的冰與結構物的作用過程提供支撐。

1 基于常規近場動力學的彈塑性本構模型

1.1 基于常規近場動力學的彈塑性理論

1.1.1 近場動力學理論

近場動力學方法將連續介質離散為均勻的物質點。在參考坐標系下，其運動方程為

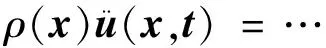
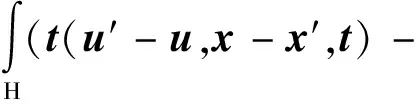
t′(u-u′,x′-x,))dH+b(x,t)

(1)

上式的離散形式為

t′(u(k)-u(j),x(k)-x(j),t))dV(j)…+b(k)

(2)

式中，每個粒子的信息用其位置坐標表示，即x(k)，該粒子占據的空間大小為V(k)且密度為ρ(k)。在笛卡爾坐標中，材料點受到外界作用的位移為u(k)，此時的位置向量為y(k)。由此，材料點k在未變形狀態下的位置為x(k)，其位移和外力向量分別用u(k)(x(k),t)和b(k)(x(k),t)表示，對k點有作用的域(近場域)表示為Hx(k)。

1.1.2 塑性理論

本文將海冰視作各向同性的均勻介質材料。下述本構模型的建立基于該假設成立。根據經典連續介質力學中的塑性定義，當材料在加載/卸載條件下的應力水平超過屈服應力時，材料在完全卸載時會發生永久(或塑性)變形。與彈性變形不同，塑性變形取決于加載歷史。因此，塑性變形更加關注每一時間步力密度增量和拉伸增量的關系。用PD進行塑性分析時，需要對等效應力進行描述，這是因為在塑性分析中，彈性區域受屈服面限制。此外，屈服面在每個加載步驟中的增長和移動都需要確定，因此需要將等效塑性拉伸描述為硬化內變量。

為了用參量的增量形式表達PD中的塑性變形，將外界作用下兩個材料點之間的拉伸增量Δs(k)(j)以及力密度增量Δt(k)(j)分解成彈性項和塑性項如下:

(3)

(4)

本文的塑性理論中假設塑性變形與體積變形無關，由此塑性拉伸的過程體積膨脹為0，即Δθp=0。PD方法中靜水壓力分別在力密度函數和應變能密度的彈性項中，用p=-kθ表述，其中k為冰的體積模量。本文模型中塑性變形與靜水壓力無關。同樣地，每一步的應變能密度增量分解為彈性應變能密度增量和塑性應變能密度增量如下:

(5)

1.1.3 屈服函數

傳統的塑性理論中，塑性變形由屈服面來判定。參照傳統塑性理論屈服面定義為[28]

(6)

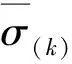
(7)

依據Von-Mises 塑性屈服準則，塑性屈服發生在偏斜應變部分的應變能密度達到極限值的時候，對于單軸壓縮來說，這個極限值等于材料達到初始屈服應力σ0時的應變能密度，即

(8)

式中J2為應力偏張量的第二不變量。為了在一般荷載情況下使用該方程，需要定義等效應力。等效應力可定義為[29]

(9)

1.1.4 流動法則和硬化規律

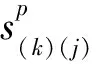
(10)

式中，C(k)為一個正比例常數，上式作為常態條件表述了塑性伸長增量的流動法則。

在式(7)中，理想塑性(無硬化)狀態下，所有加載/卸載過程中，σy是恒定的。然而，塑性變形在不同的狀態下與等效塑性拉伸具有相關性，這種相關性有多種情況，例如各向同性硬化關系、運動硬化和混合硬化關系等[28]。本文采用線性各向同性硬化模型[29]，即式(6)可改寫為

(11)

其中

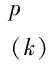
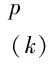
在簡單的單軸拉伸情況下，無膨脹項，可以確定塑性增量拉伸引起的畸變應變能密度，并由此提取參數A0。參數A0已在文獻[30]中針對不同的物體維度推導得出，本文未列出。

1.2 邊界條件

由于PD運動方程不包含任何空間導數，因此一般不需要約束條件來求解積分微分方程。與局部理論不同，邊界條件是通過非零體積的虛擬邊界層施加的。基于數值實驗，Macek等[30]建議虛擬邊界層的范圍等于領域尺寸δ，以確保施加的規定約束在真實區域中得到準確反映。位移邊界條件可以通過對虛擬層中的材料點進行約束來施加，使邊界曲面上的條件得到明確滿足。因此，虛擬層中的位移值可以基于實域值和邊界條件指定值的線性外推來近似。類似地，也可以通過近似虛擬區域中的牽引力值來施加牽引力邊界條件，從而使真實區域和虛擬層中的牽引力變化恢復邊界表面上施加的牽引力。圖1表示了位移邊界條件的施加方式，圖中Rf表示虛擬粒子邊界，寬度為δ，R為真實粒子區域，位移和速度邊界條件為U*和V*。則邊界條件可以表達為：

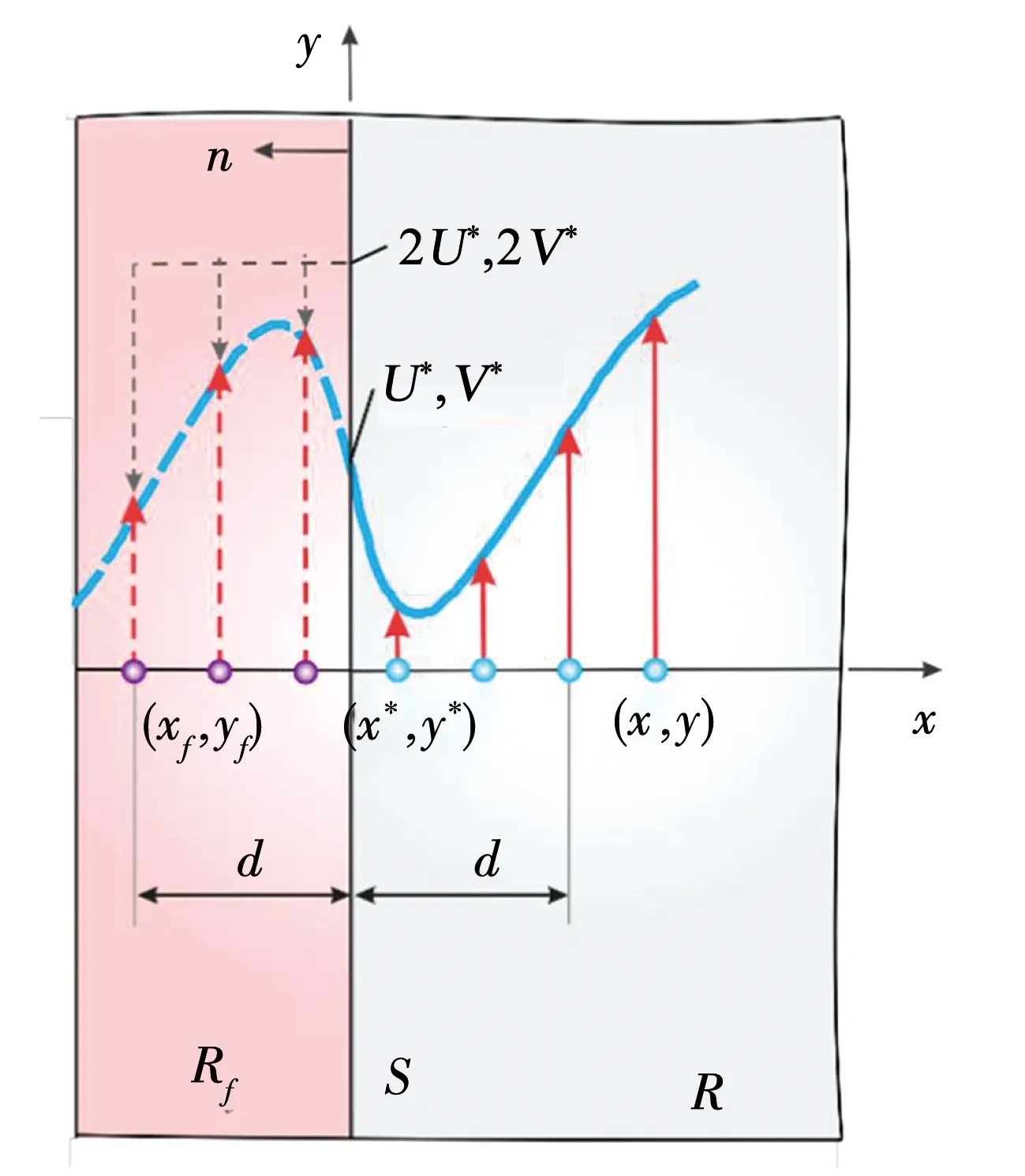
圖1 位移和速度約束條件[31]Fig.1 Boundary condition of displacement and velocity[31]

uf(xf,yf,t+Δt)=2U*(x*,y*,t+Δt)-u(x,y,t)

vf(xf,yf,t+Δt)=2V*(x*,y*,t+Δt)-v(x,y,t)

(12)

1.3 失效準則

基于PD方法的彈性變形中，失效的判斷標準為極限伸長量，當變形后粒子間的伸長量達到極限伸長量s0時，則判斷為失效，此過程不可逆。極限伸長量可以通過材料的極限能量釋放率得到，粒子間的伸長量和力密度的關系呈線性。然而在塑性變形中，粒子間力密度和伸長量的關系呈典型的非線性，如圖2所示，因此彈塑性本構模型中的失效準則不能再簡單地使用最終狀態的伸長量來判斷，必須對整個變形過程伸長量對應的力密度積分來判斷材料的失效。圖2曲線下的面積代表彈塑性變形微勢w(k)(j)，該函數代表變形的程度，可由下式得到:

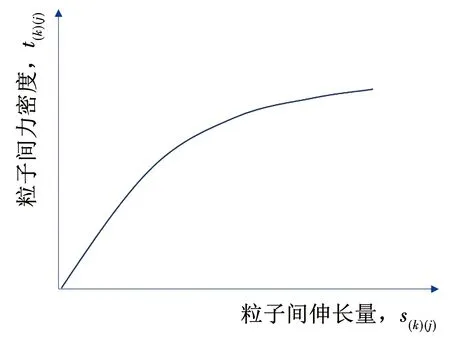
圖2 塑性理論中的變形本構關系Fig.2 Constitutive relationship in plastic deformation

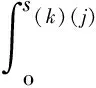
(13)

如果一個新的裂紋產生，則穿越這個裂紋的所有粒子間的作用都必須消失。同理，消除兩個粒子間作用所需的極限能量釋放率作為判別粒子間作用是否失效的標準，則可以表達為

(14)

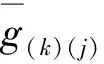
(15)

(16)

式中：Gc為材料的極限能量釋放率，Nc為PD的對應參數，在一維時取值為12，二維時取值為36，三維時取值為560。

粒子作用的失效通過上述準則判斷之后，失效的粒子作用之間力將被移除。此時，通過監測粒子之間相互作用的失效與否就可以表述材料的破壞過程。因此引入局部破壞系數φ(x(k),t)來表述材料在局部位置的破壞程度，該參數的物理意義是：材料點k在其作用域內失效粒子作用與總粒子作用的比值，由下式計算：

(17)

2 數值執行過程

2.1 數值執行策略

PD方法的控制方程主要采取積分形式，因此在數值實現時，計算域被分解成粒子形式。計算每個粒子在每個時間步長的物理信息，作為下一時間步的基礎值，每個時間步下對所有粒子的物理信息求和積分則為該步長的變形狀態。

本文參考了文獻[24]中給出的鍵型PD的程序基礎框架。本文的數值執行過程在上述程序框架進行補充完善。首先，常規型PD積分過程中增加了體積膨脹項，可按下式數值執行:

(18)

時間積分內的數值執行過程將全部替換為塑性變形的數值過程，可參考文獻[28-29]中的數值實現方法。對于失效準則的積分過程，式(13)將采用如下積分過程實現:

t+Δtw(k)(j)=tw(k)(j)+Δw(k)(j)

(19)

(20)

局部破壞系數的數值執行形式為

(21)

數值框架流程如圖3所示。

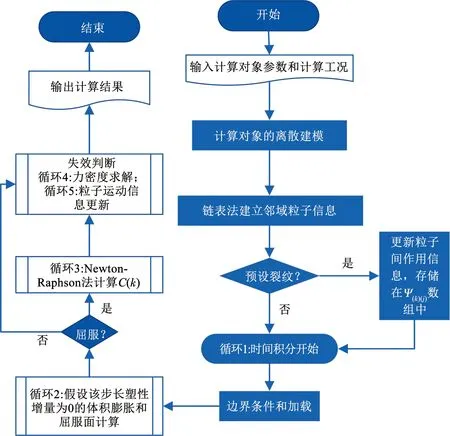
圖3 數值實現程序框圖Fig.3 Flowchart of numerical implementation

2.2 數值方法驗證

為了驗證文章模型的準確性和程序的可靠性，首先計算了帶孔二維板的變形問題。二維板的尺寸選取長和寬分別為L=H=1.0 m，板的厚度為h=0.01 m，孔的尺寸為D=0.3 m。彈性模量為E=200 MPa，密度為ρ=4 428 kg/m3，泊松比為ν=1/3，剛度模量為K=50 GPa。離散狀態的粒子間距為dx=0.002 5 m。同時采用有限元分析軟件Abaqus計算了板的有限元變形，有限元分析中，網格大小與粒子間距相同，網格數有8 910個。板的左右兩側采用位移約束，其位移變形約束表示為：ux(x=0,y,t)=-0.001 m和uy(x=L,y,t)=0.001 m。板的工況示意圖如圖4所示。

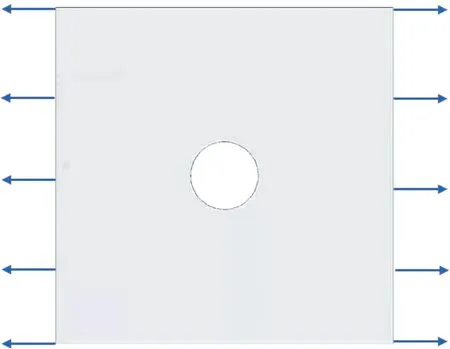
圖4 二維板拉伸變形示意圖Fig.4 Sketch map of 2D plate under tension

正如預期的那樣，塑性變形在高應力集中區域開始。圖5中給出了帶孔板的等效應力和位移的變化，與有限元結果對比完全一致，該案例驗證了本文程序的準確性。

圖5 有孔板拉伸狀態下的等效應力、x方向位移以及y方向位移Fig.5 Variations of effective stress, displacement in x direction, and displacement in y direction of plate with a hole under tension

3 冰四點彎曲數值計算

冰的彎曲強度是計算冰-船作用的關鍵參數之一，四點彎曲試驗可以用來測量冰的彎曲強度。為了驗證本文冰模型的準確性，選用Ehlers和Kujala進行的試驗[32]作為對比驗證，該試驗模型及加載工況示意如圖6所示。

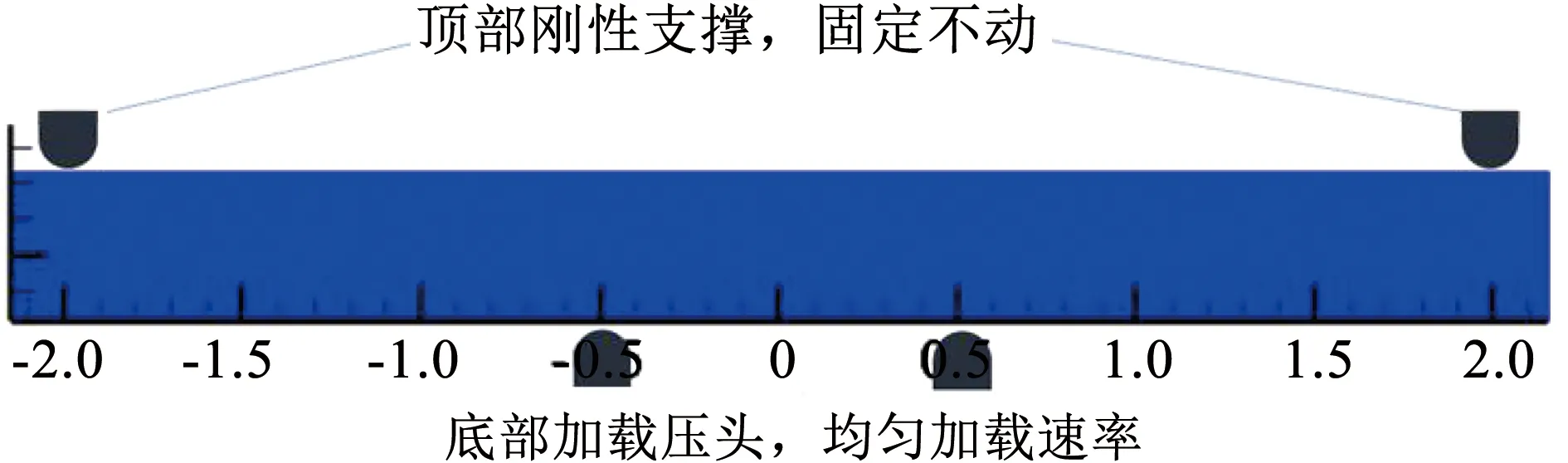
圖6 冰四點彎曲試驗示意圖Fig.6 Schematic diagram of four-point bending test of ice

該試驗中，冰梁的尺寸為L=4.25 m,H=0.4 m和B=0.365 m。上方的固定支撐位于中點向兩邊2 m處，底部位移壓頭位于0.5 m處。上方的支撐在空間中固定，下方的支撐以Vsupport=0.003 580 m/s勻速向上移動。海冰參數的選取參考試驗和文獻中對冰力學性能相關分析設定[32-34]，冰材料的極限能量釋放率采用了文獻[35]中的參考值，見表1。

表1 試驗工況設定和海冰參數Tab.1 Test conditions and parameters of ice

文中采用2D進行計算，因此彈性模量轉換成2D參數為E/(1-v2)[34]。結果如圖7、8所示。冰的彎曲載荷和時間的關系曲線如圖9所示。

從計算結果可以發現，冰梁在下部位移支撐和上層約束支撐的共同作用，發生微小變形，如圖7(a)、(b)所示，兩個移動支撐之間的冰梁位移最大，且這段部分各個位置的位移量基本相同。冰梁上越遠離移動支撐部位的縱向位移變形越小，這樣的變形一直持續到0.31 s之前。此時海冰未發生破壞，由于固定支撐和加載支撐的約束原因，冰x方向和y方向的位移符合物理規律。還可以通過等效應力分布圖觀測到：高應力分布在拉伸和壓縮集中的部位，例如冰梁的上側邊緣和下側邊緣，如圖5(c)所示，這兩側的位置是冰梁擠壓和拉伸最為嚴重的位置。該應力現象與文獻[35]中通過有限元方法計算的結果具有很高的一致性。從圖8可以觀測到：冰梁彎曲后分裂成3部分，斷裂位置對應于底部壓頭加載位置。該現象和試驗現象具有極高的一致性。另外為了進一步驗證計算結果的準確性，對比數值計算和試驗中的力-時間曲線(圖9)可知：數值計算結果和試驗結果吻合度極高。

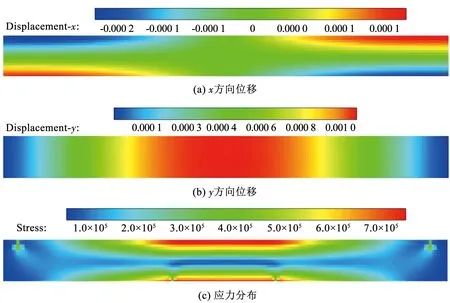
圖7 t=0.31 s,Vsupport=0.003 580 m/s(未發生破壞之前)冰四點彎曲試驗數值計算結果Fig.7 Numerical results of four-point bending test of ice (before damage) (t=0.31 s,Vsupport=0.003 580 m/s)

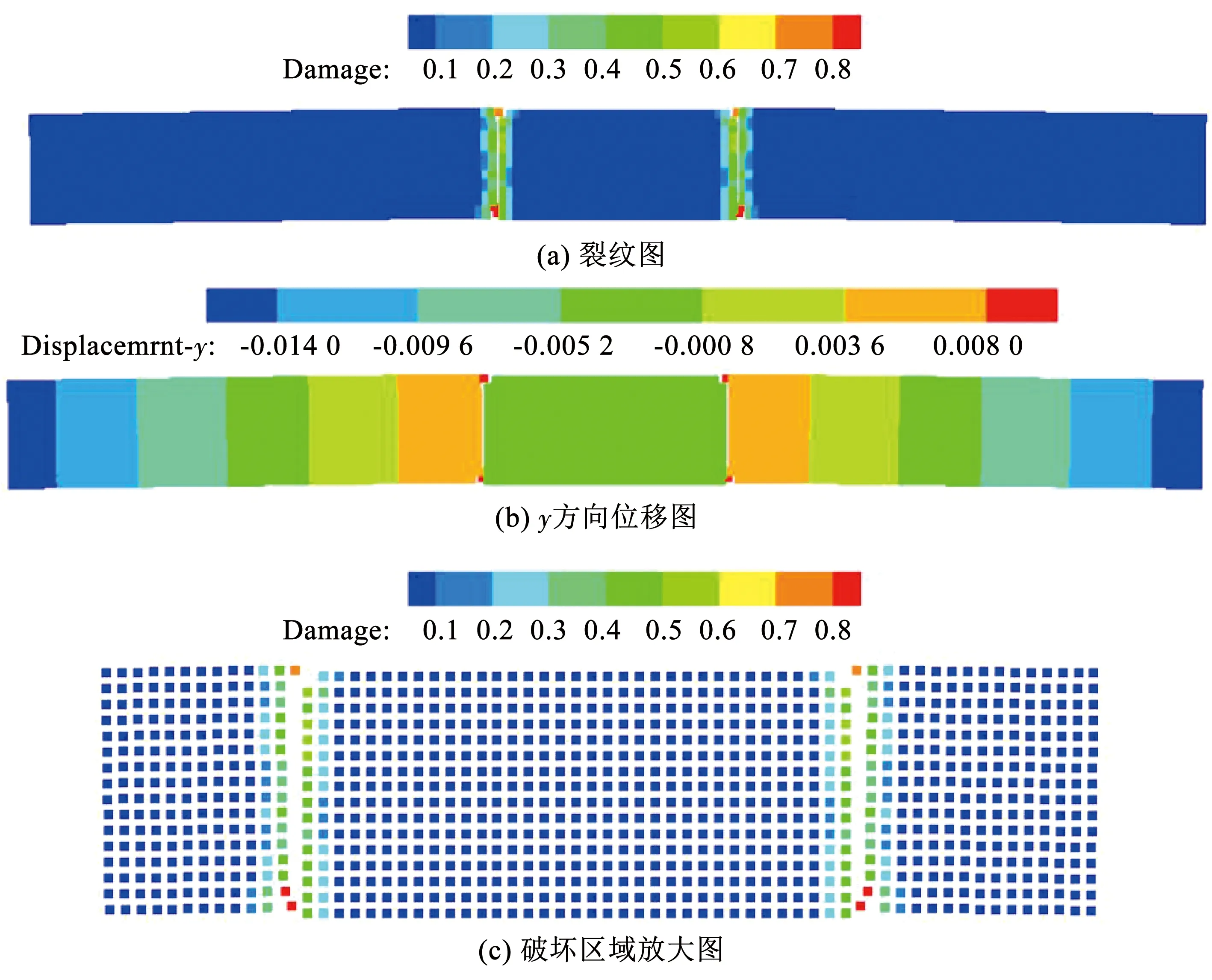
圖8 t=1.00 s,Vsupport=0.003 580 m/s(破壞之后)冰四點彎曲試驗數值計算結果Fig.8 Numerical results of four-point bending test of ice (after damage) (t=1.00 s,Vsupport=0.003 580 m/s)

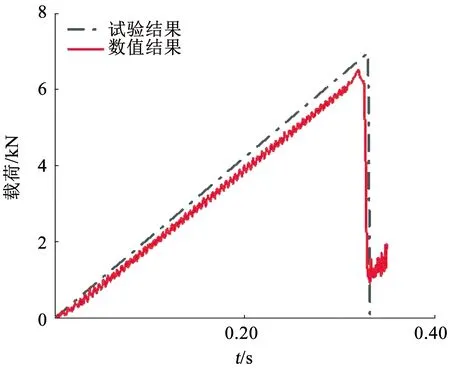
圖9 Vsupport=0.003 580 m/s冰四點彎曲載荷-時間曲線圖Fig.9 Force-time curve of four-point bending test of ice (Vsupport=0.003 580 m/s)

為了驗證本文的數值模型能夠模擬不同時間工況下冰梁的彎曲破壞，分別選取了Vsupport=0.002 750 m/s和Vsupport=0.003 147 m/s加載工況進行對比驗證，載荷-時間變化關系計算結果如圖10所示，數值結果和試驗結果基本保持一致。由試驗結果可知：加載速度為Vsupport=0.003 580 m/s時的彎曲最大載荷最大，斷裂時間最短。表2列出了3種加載速度下數值計算和試驗對應的極值載荷數值極其發生時間，從表中可以看出試驗的結果和計算值的誤差在10%以內，說明本文建立的無網格法冰本構模型能夠模擬冰的彎曲破壞過程。

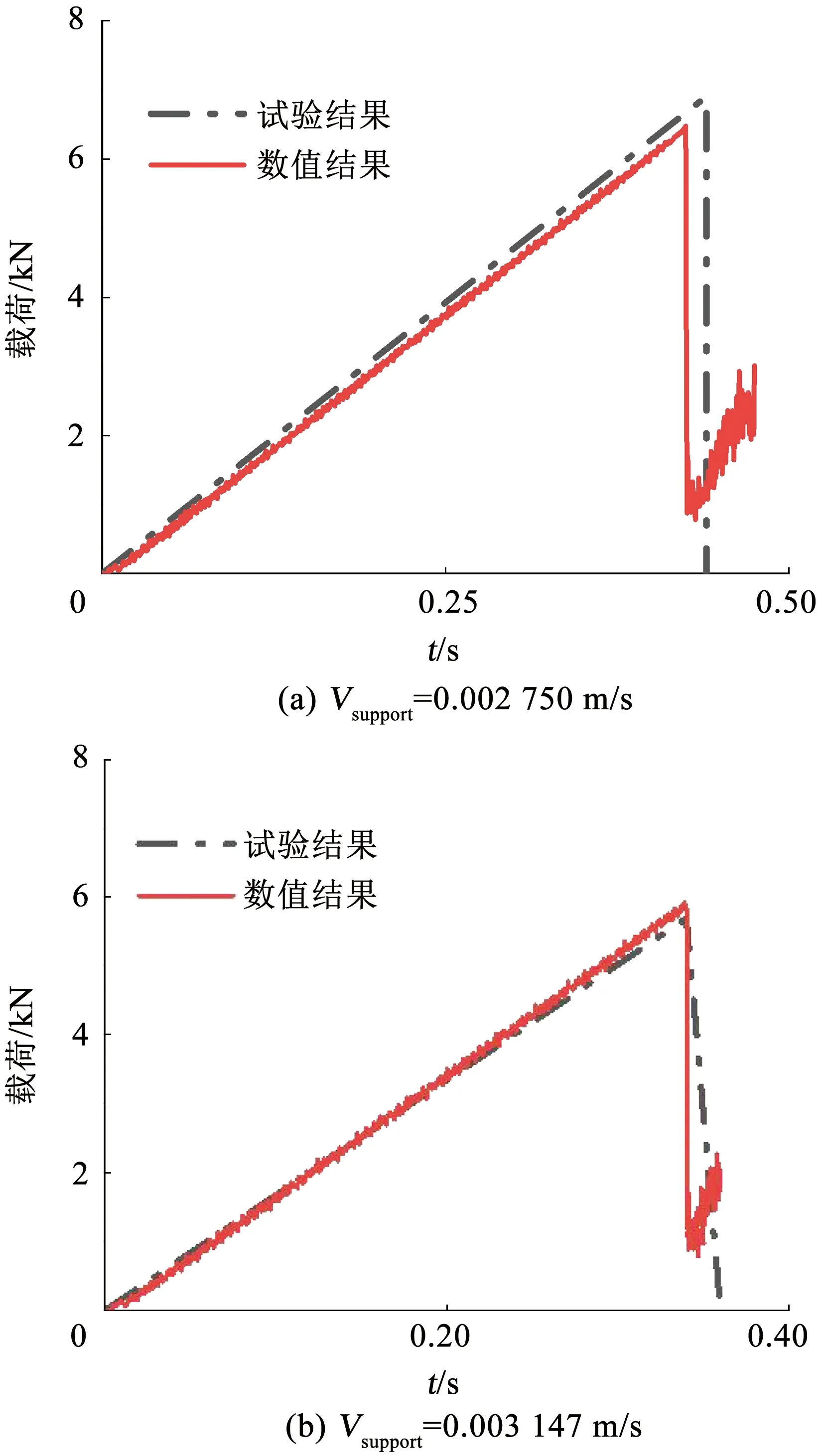
圖10 冰四點彎曲載荷-時間曲線圖Fig.10 Force-time curve of four-point bending test of ice

表2 數值計算和試驗中3種速度工況對應的計算結果Tab.2 Numerical simulation and test results under three velocity conditions

4 結 論

1)本文建立的模型能夠準確模擬冰在拉伸時的斷裂現象和裂紋擴展模式。

2)冰的四點彎曲過程中，裂紋出現在固定剛性支撐的位置。

3)冰梁彎曲后分裂成3部分，斷裂位置對應于底部壓頭加載位置。該現象和試驗現象具有極高的一致性。

4)對于冰的四點彎曲過程，加載速度為Vsupport=0.003 580 m/s時的彎曲最大載荷最大，斷裂時間最短。