考慮運動加速度干擾的無人機姿態估計算法
劉旭航,劉小雄,章衛國,楊 躍,郭一聰
(西北工業大學 自動化學院,西安 710072)
低成本無人機導航系統主要由基于微機電系統(Micro-electromechanical system,MEMS)的傳感器組成,局限于成本和功耗,噪聲誤差和偏移誤差導致陀螺儀的精度下降[1-2],僅利用陀螺儀不能實現準確的姿態估計,互補濾波被用來融合陀螺儀、加速度計和磁力計信息,獲得穩定的姿態。近年來隨著傳感器技術的飛速發展,基于互補濾波的姿態估計算法在無人系統中得到了廣泛的應用[3-5]。
傳統的互補濾波模型采用加速度計和陀螺儀作為輔助傳感器,利用陀螺儀和輔助傳感器的噪聲頻段互補的特性,減小噪聲信號對姿態估計的干擾,但是在動態環境下,載體具有較大的運動加速度,運動加速度對姿態估計的結果產生嚴重干擾,針對上述問題,國內外研究人員提出了不同的姿態估計算法。李瑞涵等[6]提出一種加速梯度姿態融合方法,利用閾值切換的方法來抑制運動加速度的干擾,該算法抑制運動加速度干擾的能力優于傳統的互補濾波算法,但并沒有給出運動加速度準確值。Euston等[7]計算向心加速度作為運動加速度,排除運動加速度對姿態估計的干擾,但是該方法未考慮切向加速度,對運動加速度的估計仍不夠精確。匡敏馳[8]設計了一種新型的垂直/水平歐拉角姿態解算方法,利用慣性器件、磁力計、全球定位系統(Global positioning system, GPS)和空速計的不同特性,獲得準確的姿態信息。但是該算法中運動加速度由更新頻率較低的GPS和空速計求得,系統誤差不能及時得到修正,姿態估計的精度不高。王鼎杰等[9]采用慣性導航系統(Inertial navigation system, INS)和GPS構建組合導航系統,通過擴展卡爾曼濾波(Extended Kalman filter, EKF)算法獲得實時的姿態信息和位置信息。但是該算法需要高精度且穩定的量測信息,通常采用定位精度達到厘米級的差分GPS,但差分GPS體積大,且價格昂貴,不適合在低成本無人機導航系統中使用,單點GPS成本低,但精度較低,更新頻率較慢,在使用單點GPS的導航系統中,采用經典的GPS/INS組合導航算法獲得的姿態角依然存在較大誤差。Lee等[10]設計了一種將姿態角和運動加速度聯合估計的姿態估計算法,運動加速度被建模成一階低通白噪聲過程,能夠在短加速周期內精確估計運動加速度,但是涉及數值較大的外部加速度時,該算法不能實現對運動加速度的準確估計。
現有的無人機姿態估計算法存在精度低,無法精確估計運動加速度的缺點,為解決動態環境下低成本無人機姿態估計易受傳感器噪聲和運動加速度干擾的問題,本文設計了一種考慮運動加速度干擾的姿態估計算法。首先,建立運動加速度估計模型,該模型分別從加速度計和GPS速度中求取運動加速度,利用獲得的運動加速度對加速度計原始值進行修正,從而排除運動加速度對姿態估計的干擾。然后,建立基于互補濾波的姿態估計模型,利用修正后的加速度信息和磁力計信息作為參考向量,構建誤差量作為互補濾波器的輸入,互補濾波器的輸出為修正后的陀螺儀角速度,通過基于互補濾波的姿態估計模型抑制傳感器噪聲干擾,提升姿態估計的精度。最后,利用無人機試飛過程中采集的傳感器數據,設計對比實驗驗證本文所設計算法的有效性。
1 運動加速度估計模型
1.1 模型框架
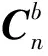
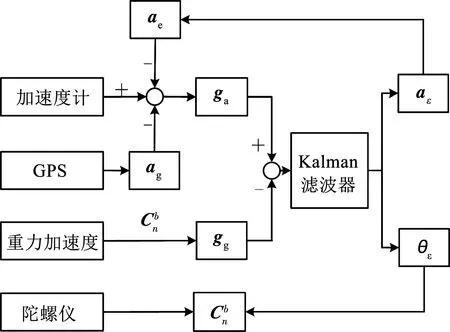
圖1 運動加速度估計模型框架Fig.1 Framework of motion acceleration estimation model
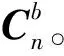
由于卡爾曼濾波器只能在短時間精確估計運動加速度ae,誤差的累積導致ae的精度逐漸下降。因此,引入外部運動加速度ag,ag由GPS速度信息差分獲得,ag的數值較為穩定,但是由于外部傳感器GPS的更新頻率遠低于導航系統姿態更新的頻率,單獨使用外部傳感器估計運動加速度會導致姿態估計的精度下降。因此,在運動加速度估計模型中,同時利用ae和ag對加速度計原始值進行修正,提升姿態估計的精度和抗干擾能力。
1.2 誤差運動加速度
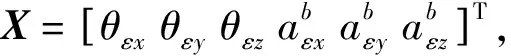
Xk=Fk,k-1Xk-1+wk
(1)
式中:Fk,k-1為狀態轉移矩陣,wk為噪聲分量。
(2)
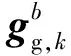
(3)
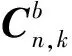
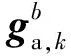
(4)
式中,ΔR( )為旋轉角度為θε,k旋轉矩陣。
由式(4),系統量測方程為
(5)
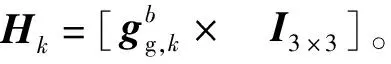
由于濾波后得到運動加速度誤差aε和姿態角誤差θε分別對運動加速度和姿態角進行了修正,修正后的誤差量為零,因此,相鄰時刻的狀態變量不相關,更新后的狀態一步預測等于零,狀態一步預測方程簡化為
(6)
狀態估計方程簡化為
(7)
濾波增益為
(8)
一步預測均方誤差為
Pk/k-1=Φk,k-1Pk-1Φk,k-1+Qk=Qk
(9)
估計均方誤差為
Pk=(I-KkHk)Pk/k-1
(10)
(11)
1.3 外部運動加速度
在低成本無人機導航系統中,GPS更新周期慢于加速度計更新周期,設加速度計更新周期為T1,GPS更新周期為T2,T1和T2通常存在倍數關系,即T2=nT1,其中,n為正整數。
(12)
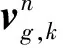

(13)
式中,dt為加速度更新周期T1。
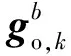
(14)
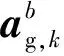
(15)
2 基于互補濾波的姿態估計
由于陀螺儀噪聲主要存在于低頻段,加速度計和磁力計噪聲主要在高頻段,因此,設計互補濾波器濾除噪聲的干擾。設陀螺儀輸出值為ωg,由修正加速度和磁力計得到的角速度修正值為ωc,載體角速度真實值為ω,則有如下關系:
(16)
式中:ng為陀螺儀低頻噪聲,nc為加速度計和磁力計的高頻噪聲。在互補濾波器中,對ωg應用高通濾波器H,對ωc應用低通濾波器L,即
ω=L×ωc+H×ωg=
(L+H)×ω+L×nc+H×ng
(17)
由低通濾波器和高通濾波器性質,有如下關系:
(18)
濾波后的角速度為
ω=(L+H)×ω
(19)
低通濾波和高通濾波的傳遞函數如下所示[13]:
(20)
(21)
L(s)與H(s)的和為1,說明經過濾波后的角速度與真實角速度相同,且不包含傳感器噪聲。
由于角速度修正值ωc來自修正加速度和磁力計,含有高頻噪聲,因此控制器一般不應含有微分項,通常采用如下形式比例積分(Proportional-integral, PI)控制器:
(22)
式中,KP、KI分別為比例和微分系數,其選值受傳感器參數和載體運動狀況的影響[14]。
基于互補濾波的姿態估計算法采用來自修正加速度和磁力計的信息構建誤差量,并將該誤差量作為PI控制器的輸入,PI控制器的輸出為角速度修正值ωc,ωc被用來消除由陀螺儀漂移和偏差帶來的累積誤差,姿態角由修正后的角速度通過方向余弦法解算。基于互補濾波的姿態估計算法的框架如圖2所示。

圖2 姿態估計算法框架圖Fig.2 Block diagram of attitude estimation algorithm
2.1 方向余弦法
方向余弦矩陣的微分方程為
(23)
其中
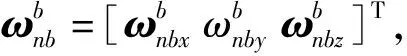
由式(23),當時間間隔dt趨向于無窮小時,方向余弦矩陣更新可以表達為如下形式:
(24)
式(24)利用陀螺信號實現了方向余弦矩陣的實時更新,利用方向余弦矩陣可以求出姿態角,姿態角與方向余弦矩陣的關系如下所示:
(25)
2.2 誤差量的計算
采用參考向量和觀測向量做外積的方式計算誤差量,誤差量由修正俯仰角和滾轉角的誤差量e1和修正偏航角的誤差量e2組成。
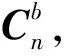
(26)
單位化的修正加速度g2為與參考向量g1相同大小和方向的另一向量,利用運動加速度估計模型計算修正加速度gb,在GPS信號未更新的時刻,gb為由誤差運動加速度修正得到,GPS信號更新的時刻,gb由外部運動加速度修正得到,即
(27)
對修正加速度單位化處理:
(28)
g2與參考向量g1做叉乘,求出誤差向量e1。
e1=g1×g2
(29)
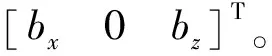
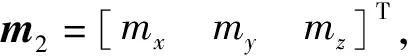
(30)
在n系的XOZ平面上和Z軸上,磁力計測量值應為同一組模值[15],即
(31)
(32)
誤差量e2由參考向量m1和磁力計輸出值m2叉乘獲得:
e2=m1×m2
(33)
總的誤差量為e1與e2的和:
e=e1+e2
(34)
2.3 PI控制器
誤差量e為PI控制器的輸入,PI控制器的輸出量存在ωP和ωI兩個分量,分別為:
ωP=KPe
(35)
ωI=ωI+KIe·dt
(36)
式中dt為方向余弦矩陣更新的周期。
綜上所述,由修正加速度和磁力計得到的角速度修正值ωc為
ωc=ωP+ωI
(37)
3 實 驗
3.1 傳感器數據采集
進行無人機飛行試驗,利用搭載于固定翼無人機的Ellipse2-N系統采集所需要的傳感器信息,Ellipse2-N系統(如圖3所示)包含了基于MEMS的慣性測量單元和GPS接收機,慣性測量單元中集成了陀螺儀、加速度計和磁力計。表1為Ellipse2-N系統的參數特性。

圖3 Ellipse2-N慣性導航系統Fig.3 Ellipse2-N inertial navigation system
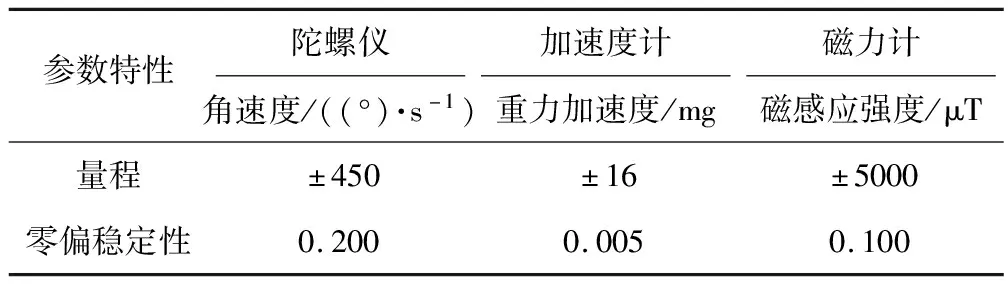
表1 Ellipse2-N參數特性Tab.1 Parameter characteristics of Ellipse2-N
利用Ellipse2-N系統采集陀螺儀、加速度計、磁力計和GPS速度信息。參考姿態為Ellipse2-N系統輸出的姿態,其滾轉角和俯仰角的誤差均方根均小于0.1°,偏航角的誤差均方根小于0.5°。GPS接收機的速度更新頻率為10 Hz,精度為0.1 m/s。采集時長為80 s的實驗數據,初始滾轉角為-23.60°,俯仰角為0.8°,偏航角為-80.6°。陀螺儀、加速度計和磁力計的采集頻率均為50 Hz,GPS速度的采集頻率為10 Hz,無人機在該段時間內盤旋飛行。
3.2 運動加速度估計模型的驗證
首先利用時長為3 s的傳感器數據進行仿真實驗,驗證運動加速度估計模型的估計效果。ga為加速度計輸出值的模值,go是僅使用外部運動加速度修正后的得到的加速度的模值,ge為僅使用誤差運動加速度修正后得到的加速度的模值,gp為使用運動加速度估計模型獲得的加速度的模值。gl為當地重力加速度的模值。圖4為加速度模值的對比圖,表2為由不同算法得到的加速度模值的統計特性。
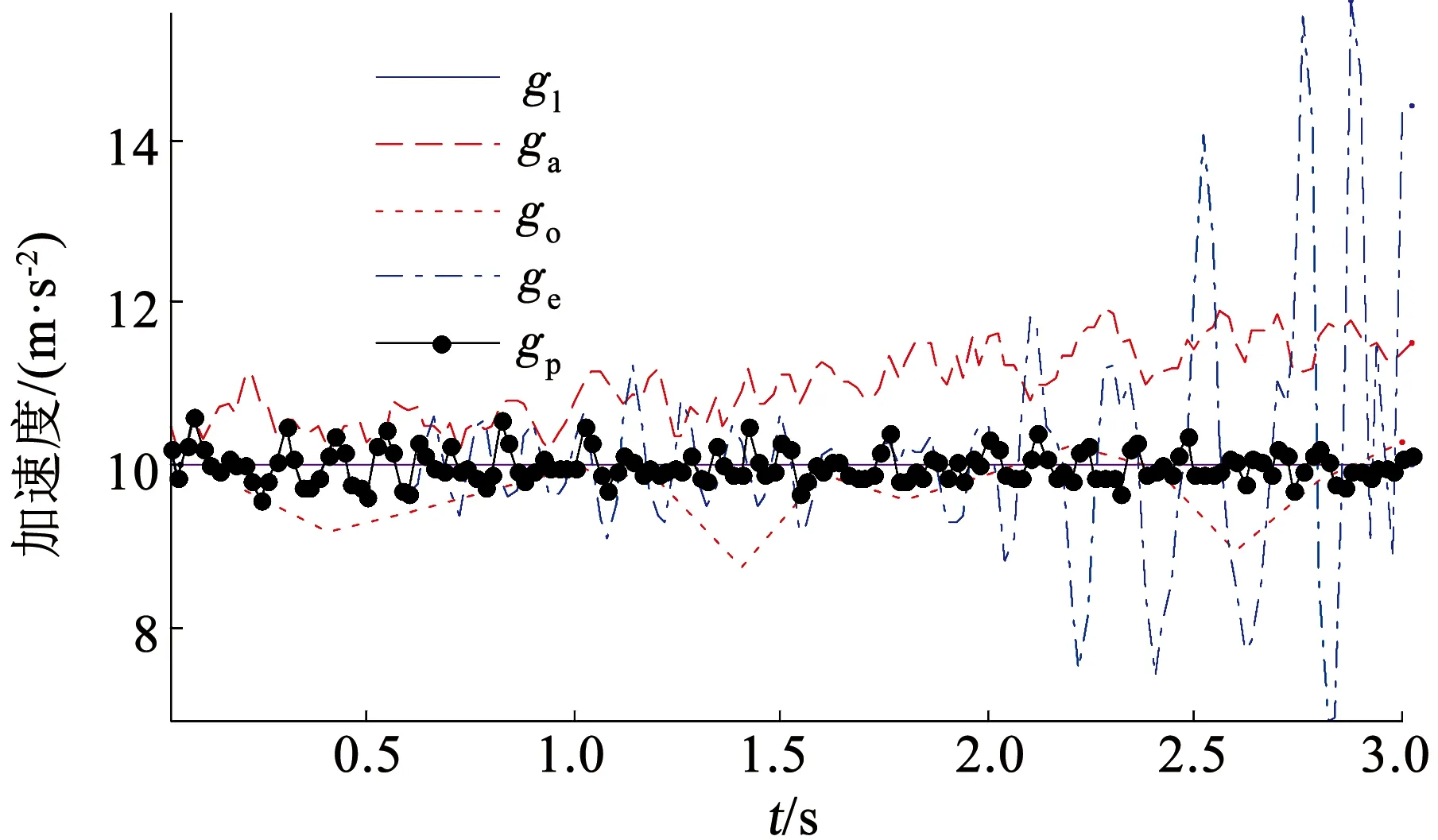
圖4 加速度模值對比圖Fig.4 Comparison of acceleration modulus

表2 加速度模值的統計特性對比Tab.2 Comparison of characteristics of acceleration modulus(m·s-2)
觀察圖4,加速度計輸出值的模值ga變化區間為[10.2,11.9],大于當地重力加速度gl,說明載體在該段時間內具有運動加速度。由于GPS更新周期較長,go數值跳變劇烈且更新頻率較慢,ge在前1 s內數值接近gp,隨后ge偏離gl的程度迅速加大,這是由于誤差運動加速度僅能在短時間內準確估計運動加速度,gp數值偏離gl的程度最小。
采用平均絕對誤差(Mean absolute error, MAE)和均方根誤差(Root mean squared error, RMSE)來衡量觀測值同真值之間的偏差,觀察表2,gp所對應的的MAE值和RMSE值最小。
綜上所述,利用運動加速度估計模型對加速度計原始值修正后得到的修正加速度最接近真實的重力加速度,運動加速度估計模型對載體運動加速度估計的精度最高,可以有效抑制動態環境下運動加速度對加速度計測量值的干擾。
3.3 考慮運動加速度的姿態估計算法驗證
利用時長為80 s的傳感器數據對所設計的考慮運動加速度干擾的姿態估計算法進行驗證。參考姿態角來源于Ellipse2-N慣性導航系統,記為RE,本文所設計算法得到的姿態角記為PR。圖5為加速度計輸出模值,圖6為姿態角對比圖。
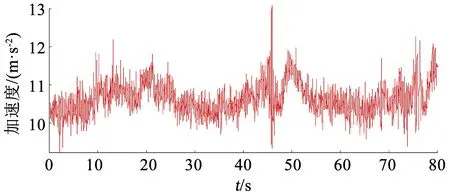
圖5 加速度計輸出模值Fig.5 Output modulus of accelerometer
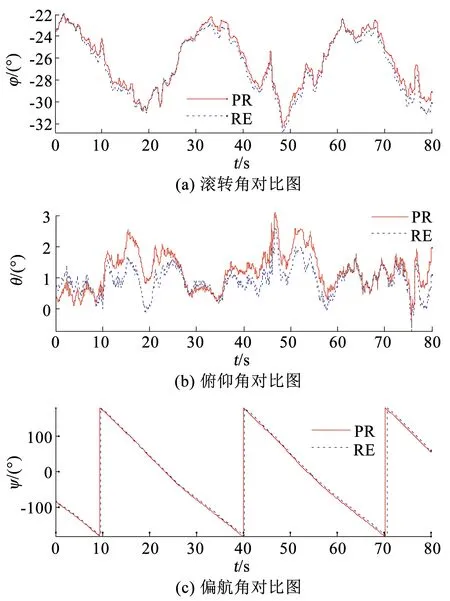
圖6 姿態角對比圖Fig.6 Comparison of attitude angle
圖5中加速度計輸出模值變化區間在[9.3, 12.9],表明載體具有運動加速度。由圖6可知,本文所設計的算法估計得到的滾轉角和俯仰角與參考值之間的誤差均小于1°,偏航角與參考值之間的誤差小于2°。因此,在具有運動加速度干擾的高動態環境下,本文所設計的姿態估計算法能夠給出穩定可靠的姿態。
3.4 不同姿態估計算法的性能比較
分別采用不考慮運動加速度的互補濾波姿態估計算法和基于EKF的GPS/INS組合導航算法,以及本文所設計的算法,同時處理時長為50 s的傳感器數據,將不考慮運動加速度的互補濾波姿態估計算法的估計值記為CF,GPS/INS組合導航算法的估計值記為EKF,考慮運動加速度的姿態估計算法的估計值記為PR。圖7為加速度計輸出模值,圖8為姿態角誤差對比圖所示,表3為3種算法的誤差統計特性。
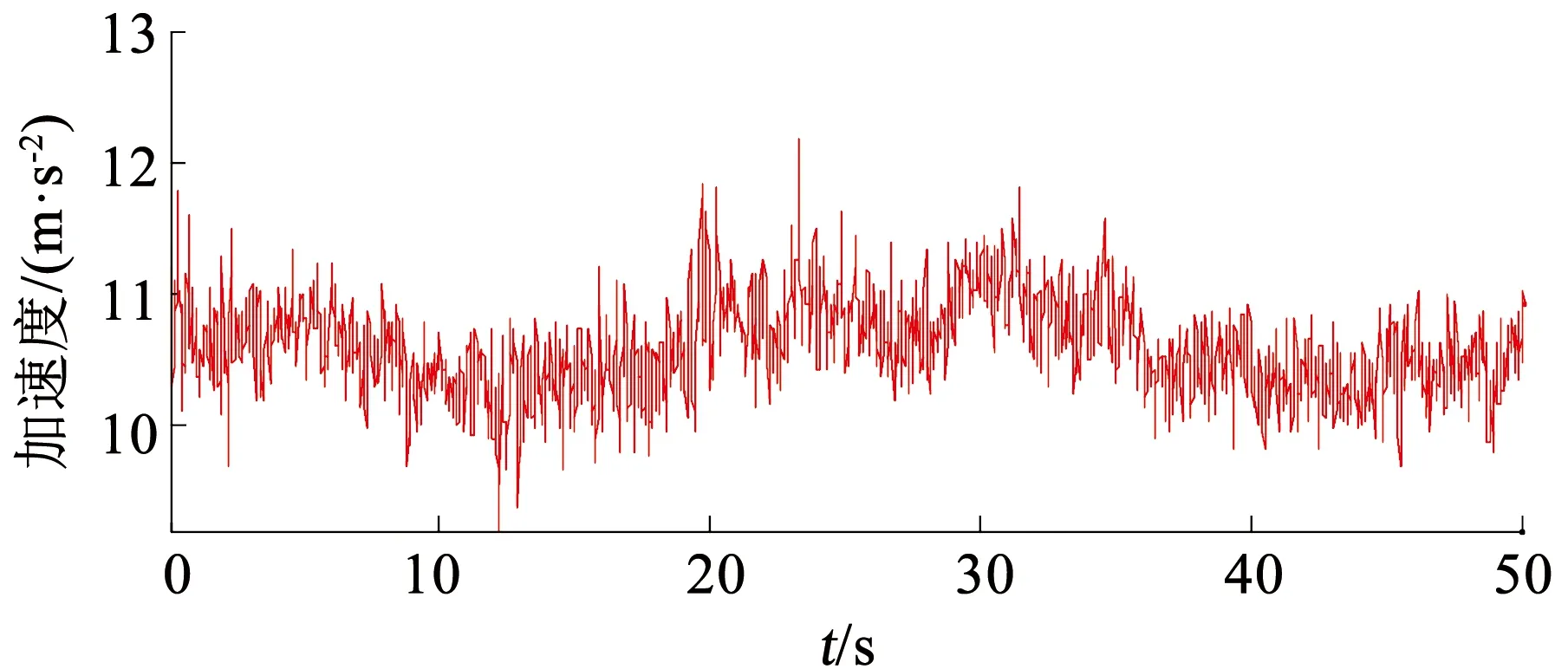
圖7 加速度計輸出模值Fig.7 Output modulus of accelerometer

圖8 姿態角誤差對比圖Fig.8 Comparison of attitude angle error
圖7中加速度計輸出模值變化區間為[9.3,12.2],即載體在該段時間內具有運動加速度。由圖8可知,在存在運動加速度干擾的情況下,考慮運動加速度的姿態估計算法的俯仰角和滾轉角的誤差值均小于1.2°,偏航角誤差值小于1.3°。原始的互補濾波算法由于運動加速度的干擾,俯仰角誤差和滾轉角誤差分別達到7.6°和4.8°。偏航角誤差達2.1°,且呈發散趨勢。基于EKF的組合導航算法受限于單點GPS速度的較差的性能,其俯仰角誤差值和滾轉角誤差值與本文所提出算法的對應的誤差值類似,但偏航角誤差值大于1.6°,遠大于本文所提出算法的偏航角誤差值。
進一步觀察表3中不同算法的姿態角誤差的統計特性,本文所設計算法姿態估計的平方絕對誤差和均方根誤差均小原始互補濾波算法和基于EKF組合導航算法所對應的平方絕對誤差和均方根誤差,即本文所設計算法姿態估計的性能優于原始互補濾波算法和基于EKF的組合導航算法,該算法能夠有效提升無人機導航系統在動態環境下姿態估計的精度。
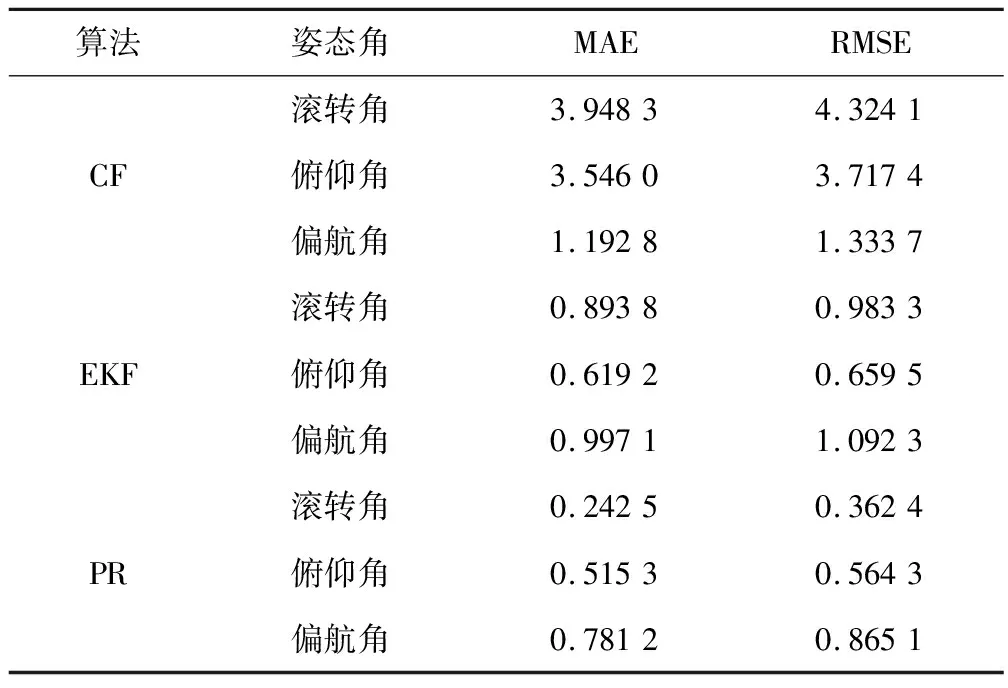
表3 姿態角誤差的統計特性對比Tab.3 Comparison of characteristics of attitude angle error (°)
4 結 論
1)動態環境下,無人機機動所產生的運動加速度和低成本傳感器固有的噪聲對導航系統姿態估計存在嚴重的干擾,針對這一問題提出了一種考慮運動加速度干擾的姿態估計算法。
2)該算法首先利用運動加速度估計模型精確估計運動加速度,避免運動加速度對姿態估計的干擾。然后構建基于互補濾波的姿態估計模型,進一步減小陀螺儀的噪聲信號對姿態估計的干擾,實現準確的姿態輸出。
3)實驗結果表明,所提出算法能夠準確估計無人機運動加速度,減弱運動加速度和傳感器噪聲對姿態估計的干擾,該算法在提高低成本無人機導航系統姿態估計的精度和抗干擾能力方面具有較高的實用價值。

