基于FPA-ELM模型的中長期徑流預測
——以雅礱江流域為例
洪 敏,艾 萍,2,岳 兆 新
(1.河海大學 水文水資源學院,江蘇 南京 210098; 2.河海大學 計算機與信息學院,江蘇 南京 211100; 3.南京工業職業技術大學 計算機與軟件學院,江蘇 南京 210023)
0 引 言
流域水文系統是一個復雜的動態系統,影響中長期徑流過程變化的水文要素具有復雜的時空變異性。目前還沒有一個通用、完善的預測模型可適用于所有情況及地區的中長期徑流預測,且預測模型中的智能算法選擇也在很大程度上影響中長期徑流預測效果。一直以來,以BP神經網絡(Backpropagation Neural Networks,BPNN)為代表的智能算法廣泛應用于徑流預測領域[1-3],但在訓練過程中,模型參數難以準確確定,因而整體預測效果欠佳。相比上述模型,極限學習機[4-5](Extreme Learning Machine,ELM)具有模型結構簡單、通用性好、計算速度快等優點,被廣泛應用于干旱、水文預報等諸多領域。但該模型的參數選取具有隨機性,導致模型的魯棒性不強,尤其是部分隱含層節點在實際應用中可能無效[6]。Yang[7]受自然界中花朵授粉行為啟發,提出了花授粉算法(Flower Pollination Algorithm,FPA)。該算法具有結構簡單、控制參數少、魯棒性強及計算效率高等優點[8]。相比于遺傳算法(Genetic Algorithm,GA)和粒子群(Particle Swarm Optimization,PSO)等生物啟發式算法,FPA不僅具有較強的收斂速度和尋優能力,而且在收斂精度和搜索能力等方面更有優勢[9]。
因此,本文提出了一種花授粉算法優化極限學習機模型的中長期徑流預測方法(FPA-ELM),并應用于雅礱江流域中長期徑流預測中。通過與BPNN、支持向量機(Support Vector Machine,SVM)、ELM和GA-ELM等數據驅動模型進行比較分析,驗證了本文所提算法具有更好的預測效果,可為基于智能算法的中長期徑流變化趨勢預測提供借鑒。
1 研究方法
本文以中長期徑流預測分析為目標,主要分為數據組織、因子篩選、預測模型構建和結果評價4個方面。數據組織主要包括流域徑流整體趨勢變化因子構造和氣候及降雨數據處理;因子篩選是通過信息熵方法計算得到影響徑流的顯著因子集合;預測模型為花授粉算法優化極限學習機模型,構建FPA-ELM模型,完成中長期徑流預測;模型評估是選用水文預報領域常用的評價指標,綜合評價預測模型的性能。
1.1 流域徑流整體趨勢變化因子構造
模型的輸入數據主要包括兩個來源:① 基于流域地形與站點空間分布的位置特征,構建能夠反映流域徑流整體趨勢變化的綜合因子;② 影響流域徑流產生的降雨數據與氣候相關數據。
依據粒計算理論,以水文站點的流域控制面積占比為權重乘以每個站點的月平均徑流量,構造流域徑流整體趨勢變化因子(Comprehensive Runoff Index,COM),用以描述流域徑流的情勢變化。流域徑流整體趨勢變化因子構造方法如下[10-11]:
(1)
(2)
式中:Wi為第i個水文站點的權重;Qi為第i個水文站點的控制面積百分比;m為流域內月均徑流一致性較好的水文站點個數;Cj為第j個月的徑流趨勢變化因子;Cij為第i個水文站點第j個月的月均徑流量。
1.2 基于信息熵的因子篩選
1.2.1偏互信息原理
當前,影響徑流過程變化的關鍵因子的篩選方法主要包括相關系數法、先驗知識法、信息熵法及主成分分析法[12-14],且每種方法都有各自適用的領域范圍。其中,偏互信息法是基于信息熵的因子篩選方法,適用于備選因子間的線性和非線性相關關系。相較于上述幾個常用的因子篩選方法,偏互信息法具有減少變量的冗余度、提高因子的篩選速度等優點,因此更適用于中長期徑流過程變化的因子選擇。
偏互信息計算方法如下:
(3)
x′=x-E[x|z]
(4)
y′=y-E[y|z]
(5)
式中:PMI為偏互信息;fX′,Y′(x′,y′)為變量X′與Y′的聯合概率密度函數;fX′(x′)為X′的邊緣概率密度函數;fY′(y′)為Y′的邊緣概率密度函數;E表示數學期望值;x表示輸入變量;y表示預測對象;z表示已入選的輸入變量集合。
偏互信息離散計算方法如下:
(6)
式中:N為離散樣本個數;i為觀測樣本編號;fX′,Y′(xi′,yi′)為(xi′,yi′)處的聯合概率密度估計;fX′(xi′)為xi′處的邊緣概率密度估計;fY′(yi′)為yi′處的邊緣概率密度估計。
1.2.2基于PMI的變量選擇步驟
當輸入變量有多個時,由于多個變量之間可能存在某種相關關系,例如X,Z為輸入變量,Y為輸出變量,則輸入變量X與Z之間可能存在相關關系,則互信息I(Y,Z)的值可能會大于實際值。因此,本文基于條件期望方法將變量Y和Z中包含的有關X信息剔除,變量間的相關度通過偏互信息PMI來度量。剔除X后,Y記為u,Z記為v,具體定義為
(7)
u=Y-mY(x)
(8)
v=Z-mZ(x)
(9)
Y和Z之間的偏互信息轉化為
PMI(Z,Y)=I(v,u)
(10)
假設C為輸入變量集,Y為輸出變量,S為預測模型的關鍵輸入變量集合,Cs為候選變量,對應PMI值最大時的輸入變量集合,那么基于PMI的變量篩選步驟如下:
(1) 初始化S,且S為空集;
(2) 如果C是空集,返回步驟(1);
(3) 計算u=Y-mY(S);
(4) 對于Cj∈C的每個元素,計算v=Cj-mCj(S);
(5) 如果I(v,u)最大時,選取候選變量Cs;
(6) 計算赤池信息準則AIC值,如果AIC值降低,則將Cs移到最優輸入變量集為S,返回步驟(2);若AIC值增大則終止篩選。
AIC計算公式如下:
(11)
式中:ui為根據已選變量計算的Y回歸殘差;p為已選變量個數;n為采樣個數。
AIC值隨著自變量的篩選不斷減小,當AIC為最小時,最優自變量集合篩選完畢。
1.3 FPA-ELM徑流預測模型構建
1.3.1極限學習機
假設任意給定N個不同樣本(Xi,ti)。其中,Xi=[xi1,xi2,…,xin]T∈Rn,ti=[ti1,ti2,…,tim]T∈Rm,目標函數定義如下[4]:
(12)
式中:N為樣本總量;g(x)為激活函數;Wi為輸入層與隱含層的權重矩陣,且Wi=[wi1,wi2,…,win]T;βi為隱含層與輸出層之間的權重矩陣,且βi=[βi1,βi2,…,βim]T;bi為第i個隱含層神經元的偏置;oj為第j個樣本的網絡輸出值;Wi·Xj為Wi和Xj的內積;C為隱含層神經元個數。
預測值與真實值誤差最小,可表示為
(13)
即存在βi,bi,Wi使得:
(14)
用矩陣表示為
Hβ=T
(15)
(16)

1.3.2結合K折交叉驗證與花授粉算法的ELM參數優化
花授粉算法(FPA)是基于花粉傳播的自然過程,依靠其他生物體的攜帶,彼此之間形成一種合作共生關系[15]。FPA由概率常數調節全局搜索和局部搜索之間的轉換,且概率常數取值范圍為0~1。FPA算法流程如圖1所示,具體算法如下:
(1) 全局搜索的數學定義為
(17)
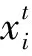
(2) 局部搜索的數學定義為
(18)

本文以上述花授粉算法為基礎,提出結合K折交叉驗證(K-fold Cross Validation,K-CV)與花授粉算法優化極限學習機模型參數的方法(算法流程如圖2所示),包括以下幾個部分:
(1) 參數初始化。假設訓練樣本為[xi,yi](xi∈Rn,n為極限學習機模型的輸入神經元數量,i=1,2,…,N,N為總樣本數量),構造極限學習機的激勵函數以及設置隱含層節點數量,其中C為隱含層節點個數,g為極限學習機模型的迭代次數。
(2) 構造極限學習機模型的適應度函數。以K-CV的均方根誤差(RMSE)作為極限學習機模型的適應度,尋找平均RMSE最小的個體。
(3) 迭代更新。計算極限學習機模型的適應度大小,并據此更新個體。
(4) 極限學習機模型最優參數生成。判斷是否達到預先設定的算法終止要求,如果達到,則獲得極限學習機模型的最優參數組合;否則,回到步驟(2)。

圖2 FPA-ELM模型流程Fig.2 Flowchart of the FPA-ELM model
1.4 評價指標
模型預測性能評價通過選用水文預報中常用的5個指標:平均絕對百分比誤差(Emape)、均方根誤差(Ermse)、確定性系數(Edc)、合格率(Eqr)及運算時間(T)等,具體計算見文獻[10]。
2 實例分析
2.1 研究區概況與數據資料
雅礱江流域位于青藏高原東部,流域地形落差大、水量豐沛,水資源豐富,因此開展中長期徑流預測具有十分重要的現實意義和應用價值。雅礱江流域及其站點分布如圖3所示。

圖3 雅礱江流域及其站點分布Fig.3 Yalong River Basin and its stations
本文的試驗數據包括前期月徑流整體趨勢變化因子、氣候、降水等624組數據,時間為1960年1月至2011年12月。具體包括兩河口、錦屏、官地和二灘等4個水文站的徑流數據、22個氣象站的降雨數據以及相關氣候數據。其中具體的氣候數據如表1所列。
2.2 流域徑流整體趨勢變化因子構造
選取兩河口、錦屏、官地和二灘4個水文站點的流域控制面積占比,根據公式(1)和(2)計算每個水文站點的權重值(見表2),再以權重值分別乘以各自站點的月平均徑流量(細粒度),最終求和得到流域徑流整體趨勢變化因子(粗粒度)構造。

表1 相關氣候數據Tab.1 Related climate data

表2 基于測站控制面積的流域徑流整體趨勢變化因子 構建權重Tab.2 Construction of weight of Comprehensive Runoff Index of watershed runoff based on the area controlled by stations
2.3 基于偏互信息法的關鍵特征因子篩選
雅礱江流域中長期徑流預測的主要特征因子包括:徑流整體趨勢變化因子fcom(fcom(t-1),…,fcom(t-11),fcom(t-12));降雨因子fr(fr(t-1),…,fr(t-11),fr(t-12));氣候因子fc1(fc1(t-1),…,fc1(t-11),fc1(t-12)),fc2(fc2(t-1),…,fc2(t-11),fc2(t-12)),…,fc21(fc21(t-1),…,fc21(t-11),fc21(t-12)),共計23×12=276個。
本文在偏互信息方法基礎上,結合了人工篩選,獲得預測模型的關鍵特征因子集,具體流程如下:
(1) 基于PMI方法計算相關性排名前20的備選因子(見表3)。

表3 基于PMI方法的備選因子相關性大小(排名前20)Tab.3 Correlation of candidate factors based on PMI method(top 20)
(2) 以上述結果為基礎,通過人工挑選方式分別從徑流整體趨勢變化因子、降雨因子和氣候因子三類對象中選取排序前5的關鍵特征因子集合,形成預測模型的最終特征因子輸入,共計13個:徑流整體趨勢變化因子fcom(t-12),fcom(t-1),fcom(t-11),fcom(t-2),fcom(t-3);降雨因子fr(t-1),fr(t-7),fr(t-12);氣候因子fc1(t-1),fc15(t-6),fc3(t-7),fc13(t-8),fc16(t-1)。
2.4 基于FPA-ELM模型的月徑流預測
2.4.1數據集劃分
基于FPA-ELM模型的月徑流預測數據集劃分為兩個部分(7折交叉驗證和模型測試)。其中,用于7-CV的數據為1960年1月至2001年12月共504組樣本數據(隨機選取6組用于訓練,余下1組用于驗證模型),測試期2002年1月至2011年12月共120組樣本數據。
2.4.2參數設置
不同算法的參數初始化設置如下:
(1) FPA:種群大小為90,最大迭代次數為600,常數P為0.8,γ為1,λ為1.5,適應度函數采用K-CV的平均RMSE,極限學習機模型的激活函數選擇“sigmoid”函數。
(2) GA:種群大小、適應度函數及ELM的激活函數類似FPA,最大遺傳代數設置為600,交叉概率為0.7,變異概率為0.01。
(3) BPNN采用7-CV方法,且結構與極限學習機模型一致,BPNN模型的訓練函數采用“tansig”函數,學習函數采用“logsig”函數,最大訓練次數設置為1 000,學習速率設置為0.1,訓練算法采用LM(Levenberg-Marquardt)算法,動量因子大小設置為0.9,模型的期望誤差設置為0.001。
(4) SVM模型采用RBF(Radial Basis Function)核函數,其中σ=0.5,懲罰參數C=1,ε=0.001。
2.4.3預測結果及對比分析
FPA-ELM與BPNN,SVM,ELM和GA-ELM等4種對比模型的交叉驗證期和測試期的性能對比如表4所列。不同模型的預測結果對比如圖4所示,預測值和觀測值及確定性系數Edc對比如圖5所示。

表4 不同模型在交叉驗證期和測試期的性能比較Tab.4 Performance comparison of different models in cross validation period and test period

圖4 不同模型的預測結果對比Fig.4 Comparison of prediction results of different models

圖5 不同模型的預測值和觀測值對比Fig.5 Comparison on observed and predicted values of different models
上述試驗結果表明:5種數據驅動預測模型均具有較好的預測效果,其中生物啟發式算法優化極限學習機模型在Emape,Ermse和Edc這幾個指標中整體上優于另外3種模型,特別是FPA-ELM模型的性能最優,驗證了本文所提算法的優越性。其中:在Emape評價指標中,FPA-ELM模型效果最好,BPNN和SVM效果較差;在Ermse評價指標中,GA-ELM和FPA-ELM模型較小,SVM模型較大;在Edc評價指標中,5種數據驅動模型的確定系數都超過了0.85,顯示了基于信息熵因子篩選方法的優勢,其中FPA-ELM模型在該項指標方面表現最佳;在Eqr評價指標中,盡管FPA-ELM模型可以應用于水文作業,但5種預測模型的整體合格率較低,其主要原因在于月徑流預測的預見期較長且影響中長期徑流預測的主要對象及其特征因子較多,導致預測的不確定性提高,因而影響整體的中長期徑流預報合格率;在運算速度評價中,FPA-ELM和GA-ELM兩種生物啟發式模型明顯優于其他3種模型,其中FPA-ELM模型表現最佳。
綜上所述,相比其他4種常用的數據驅動模型,本文所提出的花授粉算法優化極限學習機模型(FPA-ELM)在中長期徑流預測方面更有優勢。主要原因在于相較于傳統的非線性預測模型(BPNN,SVM),ELM具有模型結構簡單、通用性好、計算速度快等優點。此外,本文結合K折交叉驗證與花授粉算法,克服了傳統ELM的不足,且相比于GA算法,FPA具有較強的收斂速度和尋優能力,能夠快速搜索ELM的最優參數,因而整體預測效果較好。
3 結 論
(1) 構造了反映流域水情豐枯變化的流域徑流整體趨勢變化因子(COM),并采用偏互信息法獲得了影響中長期徑流過程變化的關鍵因子集,形成中長期徑流預測模型的關鍵特征因子輸入。
(2) 相較于BPNN,SVM,ELM和GA-ELM等數據驅動模型,結合K折交叉驗證與花授粉算法優化ELM參數構建的FPA-ELM模型,在Emape,Ermse,Edc,Eqr和運算時間等性能評價指標方面整體上優于上述4種預測模型,具有更好的預測效果,可為基于智能算法的中長期徑流預測提供借鑒。

