一種多旋翼無人機自抗擾姿態控制器

任開眾，徐 勝，蘇成悅 ，陳元電

（1.廣東工業大學信息工程學院，廣州 510006；2.廣東工業大學物理與光電工程學院，廣州 510006）

0 引言

近年來，多旋翼無人機憑借可以垂直起降、懸停和易于控制等優點，被廣泛用于航拍、測繪、農業植保、物流運輸和消防等多個領域。隨著無人機的應用場景越來越廣泛，對無人機控制的穩定性提出了更高的要求。多旋翼無人機屬于欠驅動、非線性和強耦合系統，飛行過程中容易受到風力干擾，這使得無人機姿態控制具有一定的挑戰。傳統的無人機姿態控制器是雙環串級PID，其原理簡單，易于實現，但是存在控制精度不足、調參復雜和魯棒性差的缺點，因此不同的控制策略被提了出來。

文獻［5-8］分別提出了使用非線性PID 和模糊PID 來提高無人機姿態控制的魯棒性，但仍然存在控制精度不足的缺點。文獻［9］提出了基于神經網絡的自適應滑模控制方法，計算量較大，對處理器要求高，不易于實現。文獻［10-13］均采用了自適應滑模控制策略，但是容易產生抖振現象。

自抗擾控制（active disturbance rejection control，ADRC）于1990年由韓京清研究員提出，傳統的ADRC 由二階跟蹤微分器（tracking differentiator，TD）、非線性PID 控制律（NLPID）和擴張狀態觀測器（extended state observer，ESO）組成。在ADRC 中，外擾和內擾被歸為“總擾動”。擴張狀態觀測器是ADRC 的核心部分，在ESO 中，被控對象模型被等效成串聯積分系統，總擾動被擴張成系統的一個狀態，不需要精確模型也能很好地估計出擾動來并補償掉，對噪聲抑制作用明顯，對多旋翼控制尤為適用。

文獻［16-19］都將自抗擾控制應用于四旋翼姿態控制，與PID 控制器相比，ADRC 控制器在解耦和抗干擾方面都具有良好的性能。

如圖1 所示，本文主要的創新點是在傳統ADRC的基礎上引入了一個近似模型，無人機橫滾和俯仰軸旋轉建模分別引入一階慣性模型，并在此模型基礎上根據李亞普諾夫穩定性定理設計了反步控制律來代替傳統的非線性PID 控制律。為了得到更加平滑的輸入信號的一階、二階和三階導數信號，本文采用四階線性跟蹤微分器代替傳統ADRC 的最速二階跟蹤微分器。擴張狀態觀測器同樣引入了一階慣性模型來預測被控對象的輸出，相比傳統ADRC，總擾動可以估計得更快更準。同時設計了針對參數的無人機姿態自適應調參策略，經過仿真和實際飛行驗證,此姿態控制器能保證無人機在初始參數與實際相差10 倍都不會發散，極大提升了控制器的魯棒性、調參簡易性、飛行的穩定性和安全性。

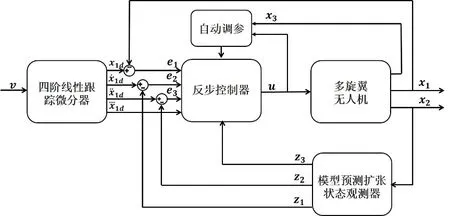
圖1 自抗擾姿態控制器

1 姿態控制建模

以X型四旋翼無人機為例子,如圖2所示。

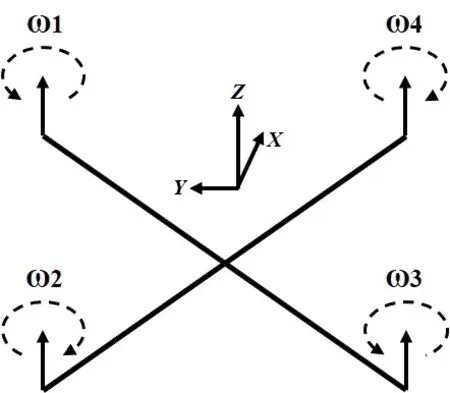
圖2 四旋翼姿態建模示意圖

假設無人機整體為一個剛體, 質量分布均勻,其姿態動力學方程可表示為：

其中:、和分別是四旋翼無人機的橫滾角、俯仰角和偏航角。l、l和l是三軸轉動慣量。τ、τ和τ為外力擾動。l為電機轉動慣量。Ω =-+-。是力臂長度。F、F和F則是電機輸出升力。

在實際應用中,對于橫滾俯仰旋轉運動，其力矩須由螺旋槳撥動空氣來產生，存在一定的延時，而偏航旋轉運動則依靠不同電機和螺旋槳自身轉速差來達到力矩輸出，故偏航旋轉模型可等效于·，俯仰和橫滾控制量到螺旋槳產生升力的過程則等效為一階慣性模型，假設電機動力參數一致，有：

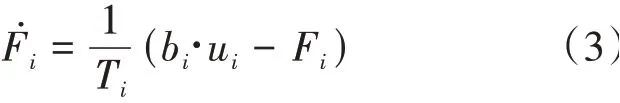
式中：可認為是螺旋槳加速的慣性時間，為增益，把式（1）中除F外的項當成未建模擾動，結合式（3）可得：

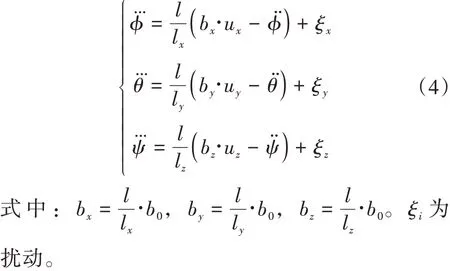
2 模型預測狀態觀測器

以X 軸為例, 選取角速度為觀測量, 根據式（4）其旋轉動力學狀態空間方程如下所示：

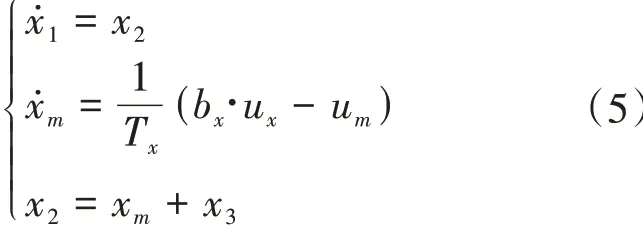
其中：、和分別是角速度、角加速度和擾動，x則是模型預測角加速度。模型預測擴張狀態觀測器設計如下：

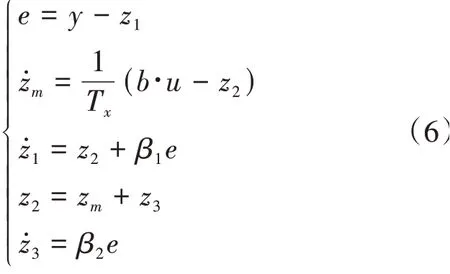
其中：、和分別是估計角速度、估計角加速度和估計擾動，z是預測角加速度，為無人機實際控制角度，和為觀測器系數。

3 四階線性跟蹤微分器

控制器帶寬有限，用來跟蹤無限帶寬的輸入信號本身不合理，并且直接對帶噪信號求導會放大噪聲而導致控制發散，因此跟蹤微分器是經典自抗擾控制中很重要的一部分。跟蹤微分器旨在獲得平滑的輸入信號及輸入信號的各階導數。如果能夠合理地提取差分信號，可以提高控制器的性能，大大簡化控制器的設計。傳統自抗擾控制采用的是二階最速微分跟蹤器，具有復雜的函數形式， 這對實際實現應用是一個挑戰。此外它僅提供一階導數信號。四階線性跟蹤微分器可以獲得更高階的導數信號用于控制律，其參數較少，易于實現，傳遞函數如式（7）所示：

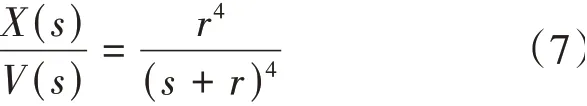
其中：為跟蹤/濾波因子，＞0。假設v() =,根據終值定理有：

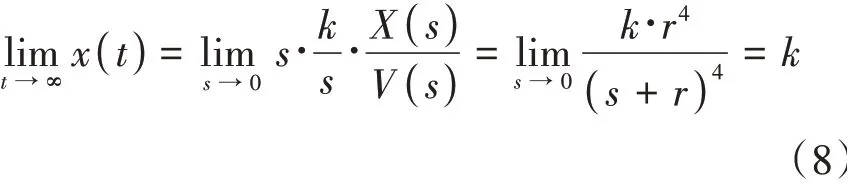
式（8）證明此跟蹤微分器的輸出最終會無誤差地收斂到輸入值,如圖3所示,其跟蹤速度由參數決定，參數越大,跟蹤越快,但是濾波性能會下降。

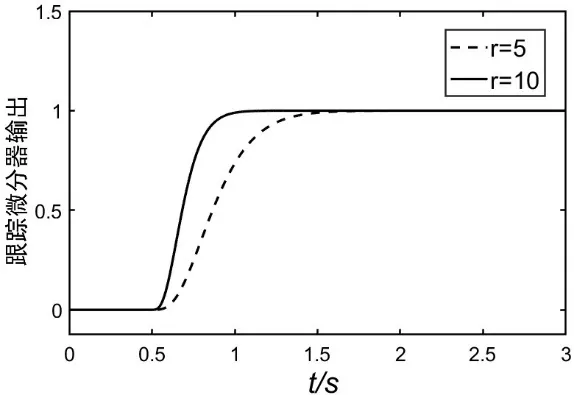
圖3 四階線性跟蹤微分器的階躍響應

此四階線性跟蹤微分器的離散形式如下所示：

式中：是輸入信號，、、、分別是跟蹤信號、跟蹤信號的一階、二階和三階導數。

4 控制律設計

選取角度為控制量,系統的狀態空間方程如式（10）所示：

其中:、和分別是角度、角速度和角加速度, ξ是系統的總擾動,包含外擾和內擾。控制器設計如下：

（1）假設目標角度為,角度誤差為,有：

定義Lyapunov 函數為：

有：

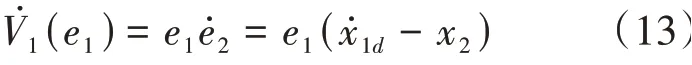
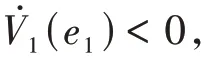
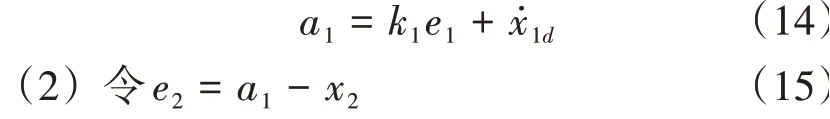
定義Lyapunov函數為：

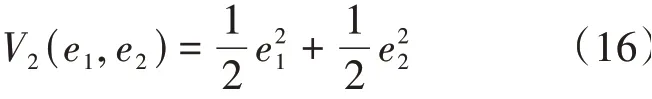
有：

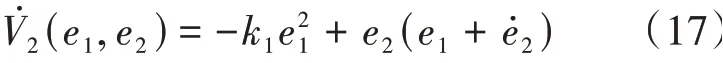
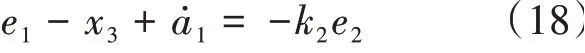
定義：

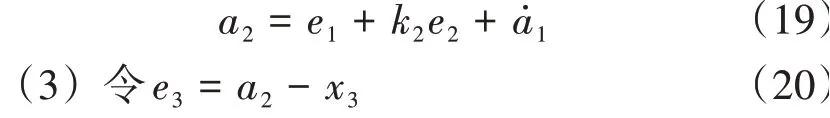
定義Lyapunov函數為：

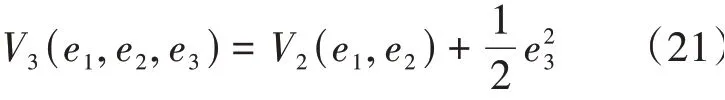
有：

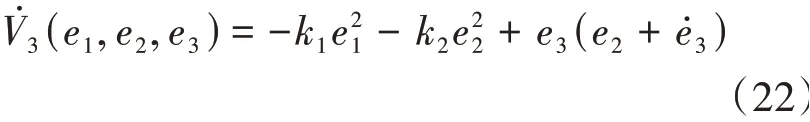
即：

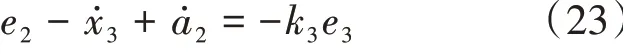
式（10）結合式（23）可得：

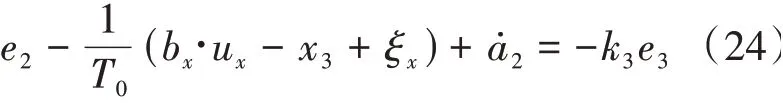
最后得到控制量輸出u為：

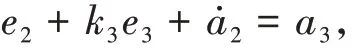
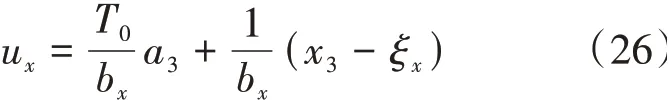
（4）反推

式（26）—式（28）即是反步姿態控制器所需的計算公式。及其各階導數由四階線性跟蹤微分器給出。

5 自適應調參策略

為解決無人機因控制參數與實際參數相差過大而導致控制發散的問題,針對參數提出一種基于批量梯度下降算法的自適應調參策略。假設無人機實際角加速度為y，控制量為u，模型預測輸出為(u)，為采樣數量選，取誤差函數()為：

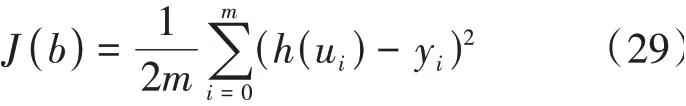
有：

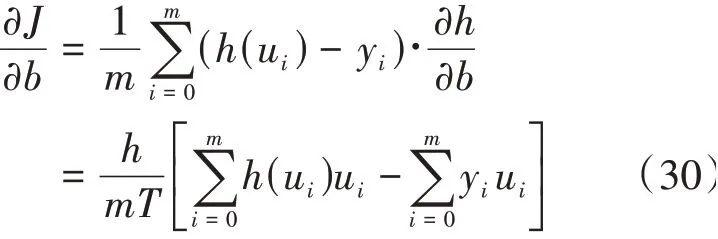
則參數：

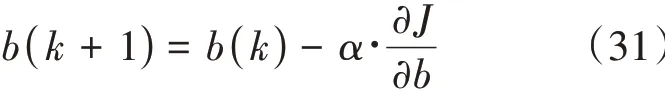
式中：為修正因子， 0＜＜1。實際應用中由于噪聲的存在，需要對u和y進行低通濾波。

6 仿真分析

本文使用Matlab 的Simulink 搭建此姿態控制器的仿真模型，結構如圖1 所示，令ESO 觀測參數=0.1，=0.001，真實姿態模型的=5.5，= 0.1，ESO 和控制的、參數為真實的模型參數，反饋增益參數= 5，= 15，=50，ESO仿真結果如下圖所示。

如圖4 和圖5 所示，和原始濾波后的數據相比，在同樣的濾波效果前提下，ESO 估計角速度和ESO 估計角加速度延時更小，極大提高了控制器的穩定性和魯棒性。擾動估計如圖6 所示， 在0.1 秒處加入階躍擾動后，傳統ESO 擾動估計并不準確，而本文的帶模型ESO 在0.15秒處即可估計出百分之八十的擾動，0.3 秒便達到了穩定狀態。

圖4 角速度對比

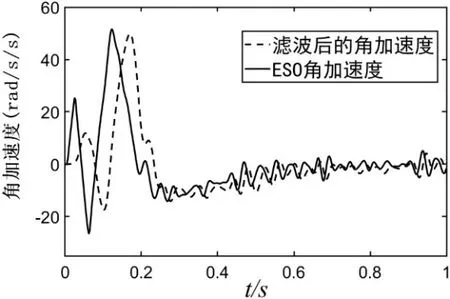
圖5 角加速度對比

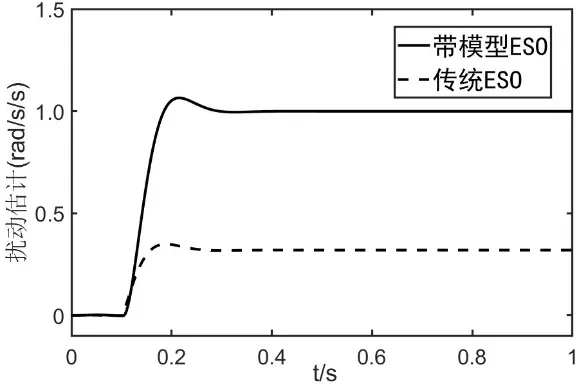
圖6 擾動估計對比

其他參數不變，令參數取值分別為24 和1.5，仿真結果如圖7 和圖8 所示，可以看到參數太大會導致角度控制超調并大幅度低頻震蕩，參數太小則會導致角度控制小幅度高頻震蕩，但都不會發散。

圖7 角度控制（b = 24，T = 0.1）

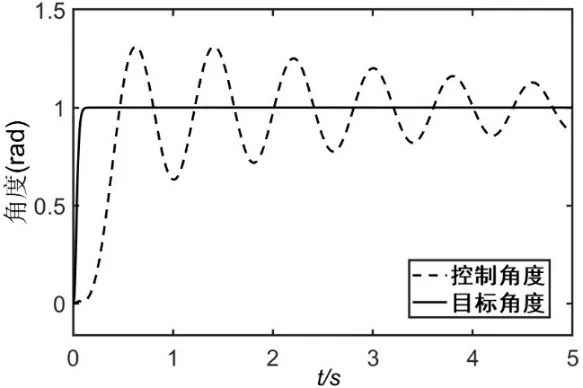
圖8 角度控制 （b = 1.5，T = 0.1）

當控制參數偏離真實參數時，角度控制也會發生震蕩，對于多旋翼無人機，實際應用中參數的范圍一般在0.05～0.2 之間，變化范圍較小，因此通過調整參數也能達到很好的控制效果，仿真結果如圖9和圖10所示。

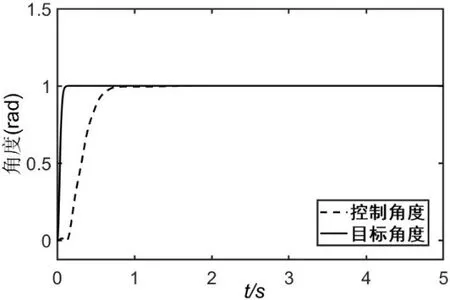
圖9 角度控制（b = 8，T = 0.2）

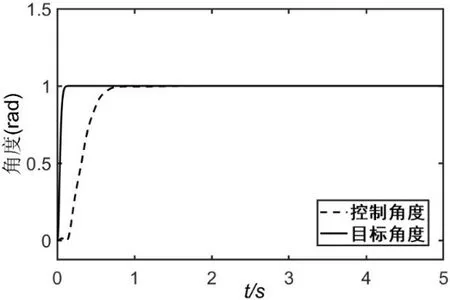
圖10 角度控制（b = 4，T = 0.05）

7 實際飛行驗證

此姿態控制算法在數十臺多旋翼無人機上進行了驗證， 包括330～1600 mm 軸距、不同動力配置的多旋翼無人機，實際測試中發現參數通常為0.1 秒左右，故只需調整參數即可， 直觀表現為參數過大無人機姿態會大幅度晃動，參數太小無人機姿態則會高頻抖動，與仿真結果一致。

圖11 測試無人機

在此控制器一般只需調整參數的前提下,為進一步提高控制器的魯棒性，引入了自適應調參策略。以330 mm 軸距的四旋翼無人機為例進行實飛測試，其真實參數和參數分別為0.1和5.5左右，設置初始參數為1和60，修正因子為0.002，參數自適應效果如圖12所示，估計參數在10秒內由60收斂到15左右，最后收斂接近于真實的參數，有效防止了控制發散。

圖12 估計b參數

8 結語

針對多旋翼無人機，本文提出了一種自適應調參的自抗擾姿態控制器。通過引入一階慣性模型，降低ESO 負擔，能夠快速估計出擾動并補償掉，結合四階線性跟蹤微分器，設計反步控制律代替傳統的非線性PID，仿真和實際飛行結果表明，對于不同軸距和動力的無人機，一般只需要調節參數即可。為了進一步提高調參的簡易性，解決因機身結構、負載和電池動力導致的參數攝動問題，控制參數與實際參數相差過大而導致的控制發散問題，提出了基于批量梯度下降的自適應調參策略，實際飛行結果證明控制參數與實際參數相差10倍都能夠迅速收斂并接近真實參數， 證明此姿態控制器具有很高的穩定性、魯棒性和實用性。