歷史大震烈度推算新方法研究*

趙懷群,陳文凱，張 燦，康燈杰

(中國地震局蘭州地震研究所，甘肅 蘭州 730000)

地震烈度指地震引起的地面震動及其影響的強弱程度[1]。歷史地震烈度的評定對地震烈度區劃、城市規劃、震災情景模擬、歷史災害研究等具有重要意義[2-3]。歷史地震的研究常關注發震構造、位置和烈度，推斷地震復發周期和影響區域，研究結果為現代震災防御提供了不可或缺的數據和技術支持。

史料記載的地震現象是評定歷史地震烈度的主要依據。收集歷史上某一地震的建筑破壞、人口傷亡、地表變化等資料，參照歷史地震烈度評定標準推斷震中烈度，根據震級和震中烈度經驗公式換算震級，然后結合史料和經驗公式對地震烈度進行評估是歷史地震烈度評定的常見流程。閔子群曾根據“新的中國地震烈度表”和“確定歷史地震烈度的補充規定”結合烈度經驗公式完成了中國歷史上64次破壞性地震的等震線編制[4]。《中國歷史強震目錄》[5]《清時期中國歷史地震圖集》[6]等權威資料中對無儀器記錄的地震也采取了這種烈度評定流程。為保持不同版本歷史地震烈度表的一致性，鄢家全等以“歷史地震烈度-震級簡表”和“歷史地震烈度表方案”為基礎，著重補充了Ⅹ～Ⅻ度標志的表述，提出了“中國歷史地震烈度表”[7]，完善了歷史地震烈度評定的指標描述。王繼等利用歷史地震等震線和歷史調查資料推斷了核動力工程廠址在歷史地震中的烈度[8]。但是，史料的數量和質量受到災區人口、經濟、受災程度等多種因素影響，一般極災區的資料最為豐富和準確，其他區域資料較少，且根據表征損害程度的文字進行烈度判斷，具有較大的主觀性。

張煒超等直接將橢圓烈度衰減關系用在了1477年銀川地震的考證研究中[9]，該方法對位置特殊、史料記載少的震例烈度評定起到了一定的參考作用，但此類經驗關系式存在明確的區域性，并受到震例選擇的影響，只適用于特定地區和震級范圍內地震烈度評估[10]。陳培善等提出采用位錯模型計算理論烈度分布，獲取的結果與調研烈度結果具有較好的一致性[11]，但模型計算過程中需要輸入較多的震源機制參數，而歷史地震往往缺乏這些參數[12]。

為避免諸如建筑設防差異、經濟條件、文化差異等人為因素帶來的地震危險性評估的不準確性，MICHETTI 等人開發了基于地震對自然環境產生影響的地震烈度表(Environmental Seismic Intensity Scale 2007, ESI-07)[13]，該表以地表破裂、構造抬升/下降、液化、滑坡、巨石的位移、海嘯、水文異常等現象評定地震烈度，為歷史地震和未來地震的危險性分析提供了標準，成為國外評定歷史地震和古地震烈度的主要方法之一。PAPATHANASSIOU等人基于該表對2014年希臘塞隆尼亞地震和1867年歷史地震的宏觀地震烈度進行了評定[14]。MAVROULIS等人利用ESI-07表完成了希臘Zakynthos島上1513年到2019年間所有破壞性地震的烈度評定工作，識別出了區域內最容易受到地質不穩定效應影響的區域[15]。該表依然以地質現象的文字描述作為烈度評定的主要依據，無法展示整個區域內的烈度分布，并且需要詳細的地質現象調研資料，同樣存在主觀判斷帶來的不準確性。

幾百年前甚至更早的地震發生時，沒有臺站和實際地表破裂量測數據。而余震區在一定程度上反映了大地震的破裂圖像[16]，強震的發震斷裂帶組合方式制約了其余震區的形狀和余震階段性的狀態[17]。因此，不少專家學者嘗試利用余震信息進行強震極災區的判定、地震烈度的評估和影響場的修正，均得到了較好的效果[18-20]。

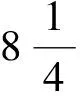
1 震例選擇與數據獲取

2 研究方法與數據處理

OHNO等人[24]提出的等效震源距物理意義明確，指從虛擬點源到某地的距離上，虛擬點提供的能量與有限大小的斷層提供的能量相同，可以將點源距離衰減關系應用在斷層附近。司宏俊[25]利用日本21次強震數據，綜合考慮不同震級、不同斷層類型和地基特點，擬合出了基于斷層最短距離和等效震源距的距離衰減式。張燦等[26]在對震災城市建筑情景模擬中，以整個馬銜山南緣斷裂帶代替地表破裂數據，結合最短斷層距模型對1125年蘭州市7級地震進行了模擬，結果表明該方法可以較好的模擬歷史地震；此外，在2021年青海瑪多7.4級地震中，利用最短斷層距模型快速獲得的地震烈度，為震后災情調查、烈度圖繪制和災害損失評估工作提供了重要的參考[27-28]。

最短斷層距模型和等效震源距模型的計算均需以震中為中心生成一定數量和大小的空間格網和格網中心點，本文三個震例設置的格網范圍均為1 000 km×1 000 km，格網單元大小為1 km×1 km，同時生成格網單元的中心點矢量文件。

2.1 最短斷層距模型

最短斷層距模型是在生成的空間格網中尋找與格網中心點三維距離最近的地表破裂點，由此計算各格網點的地震動數值。本研究采用余震點間接代替地表破裂數據和利用文獻資料繪制地表破裂數據兩種方式進行計算。公式如下：

(1)

(2)

lgPGA=0.50Mw+0.0043D-lg(R+0.0055×10(0.5Mw))-0.003R+0.61;

(3)

lgPGV=0.58Mw+0.0038D-lg(R+0.0028×10(0.5Mw))-0.002R-1.29;

(4)

lgAMP=1.83-0.66lgVS30

(5)

PGV-vS30=AMP·PGV。

(6)

其中格網點的坐標為(x1,y1)，(x2,y2)為余震震中或地表破裂數據的坐標；h為覆蓋土層的厚度(km)，取值為1，Rn為震源距離，R為斷層最短距離(km)，PGA為地震峰值加速度(cm/s2)、PGV為地震峰值速度(cm/s)，Mw為矩震級，因歷史地震震級為推斷的震級M，為方便計算，本研究直接采用M數值進行計算。D為震源深度(km)，AMP為地形放大系數，VS30為地表下30 m深度范圍內的等效剪切波速。

2.2 等效震源距模型

等效震源距模型是求解格網點與震源間的距離衰減值，因余震近似沿破裂線分布，可將每個余震震中視為一個震源進行求解。該模型可視為一個線源的烈度衰減關系，要求輸入各余震的位置坐標和釋放的相對能量值，歷史地震余震的相對能量值無法獲取，本文將其取值為1，只利用余震分布的線狀特征進行計算。其公式如下：

(7)

lgPGA=0.50Mw+0.0036D-lgR-0.003R+0.60;

(8)

lgPGV=0.58Mw+0.0031D-lgR-0.002R-1.25。

(9)

式中：R為等效震源距(km)，Rk為空間網格點距第k個余震點的距離(km)，Mk為第k個余震點釋放的相對能量值，為無量綱數值，利用公式(5)、公式(6)可計算地形對PGV的影響。

3 結果分析

3.1 余震點選擇對結果的影響

余震的震級和位置對計算結果影響較大。《中國歷史強震目錄》中記錄了郯城地震后幾次余震信息(下稱強震目錄版)，刁守中等[22]對其中7次強余震史料進行了系統的收集、整理，校訂了其基本的地震參數(下稱刁守中版)。以最短斷層距模型為例，本文對多種余震數據組合進行計算，選取的余震均沿斷層走向分布。

上述數據組合中，圖1d結果最佳。在采用最短斷層距模型計算烈度時，可優先選取的“主震+強余震”的數據組合，當強余震數據不足時，可選用主震和斷層內所有余震數據進行計算。郯城震例最佳數據組合見表1。

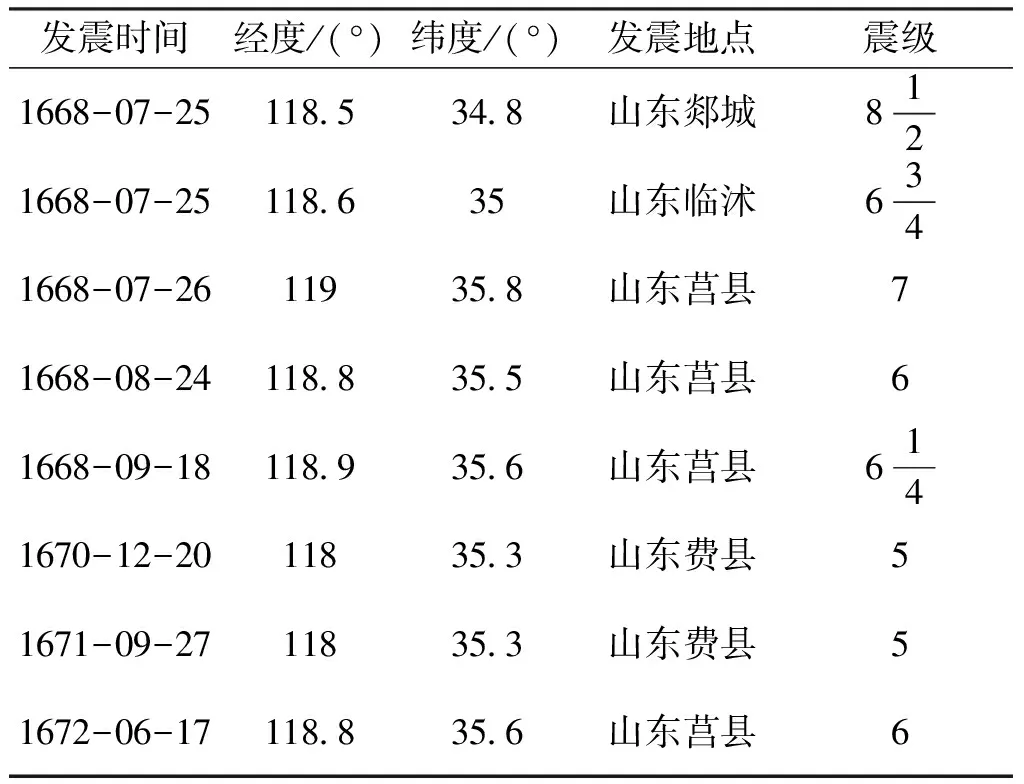
表1 郯城震例主震與刁守中版強余震

圖1 不同余震組合得到的烈度結果(審圖號：GS(2016)2556號，下同)

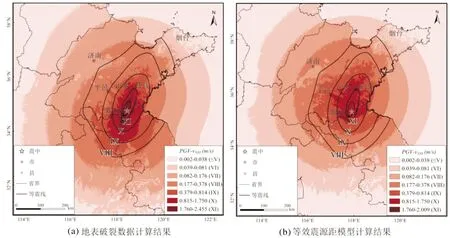
圖2 不同模型烈度結果

3.2 不同模型結果對比

為檢驗最短斷層距和等效震源距兩種衰減模型在歷史地震烈度推算中的效果，對比在最短斷層距模型中使用地表破裂線和余震點的區別，本節選取地表破裂線、刁守中版強余震和主震數據用于模型計算。

在實際應急工作中，為提高地震烈度評估速度，常在地震發生后根據區域內地表破裂經驗關系計算破裂長度，然后假設以震中為中心向兩側等長破裂進行計算。本文亦采取該方法，依據文獻中破裂數據[29]，按沿震中向兩側等長破裂的方式進行計算。圖2a中結果與等震線比較，高烈度區域(Ⅸ、Ⅹ、Ⅺ)出現向西南方向偏移的現象，但Ⅺ度范圍集中且沿斷層分布，大部分位于等震線Ⅺ度圈內，該方法計算速度快，若考慮地表破裂細節(如破裂方向、兩側長度、破裂形式等)結果應更準確，可滿足快速獲取歷史大地震烈度分布圖，且精度要求不高的需求。圖2b中，等效震源距模型計算的最高烈度(Ⅺ)集中在莒縣附近，等震線Ⅻ度圈對應結果中的Ⅹ度，各烈度結果相對等震線而言范圍略小。

最短斷層距模型與“主震+強余震”結合在歷史地震烈度推算中表現突出，圖1d最高烈度絕大部分在等震線Ⅺ度圈內，且主要集中在Ⅻ度圈內，Ⅸ度、Ⅹ度烈度范圍與等震線重合良好。因此，本文認為最短斷層距模型適合用于歷史大地震烈度推斷，且“主震+強余震+最短斷層距”方法可以滿足精度高、計算快的需求。

3.3 最佳模型結果分析

本節以《中國歷史強震目錄》中等震線為基準，對比模型結果與權威的等震線間的差異。圖3計算結果最大值(Ⅺ)范圍與等震線吻合度高，模型計算的最高值主要集中在Ⅻ度等震線內；Ⅷ、Ⅸ范圍均大于等震線，但在沿斷裂帶方向其范圍與等震線一致。此外，與高維明版本等震線對比時發現，Ⅹ度等震線的范圍和形狀與模型結果幾乎完全一致，表現了該方法對烈度區范圍推斷的可靠性。

在很多震例烈度計算中，最短斷層距模型表現出大震計算烈度小于實地調研烈度的情況，如在汶川地震的計算中，計算結果最大烈度為Ⅹ，而調研評估的最大烈度為Ⅺ，但是模型計算的范圍與實際調查烈度范圍高度一致；在2021年5月22日青海省瑪多地震中，最短斷層距模型結果也與實際烈度影響范圍高度吻合，為最終烈度圖繪制提供了參考。本文依據最新版“中國地震烈度表”對地震動參數進行分類，僅是給出數值上的烈度分布，而宏觀烈度調查時需要結合多個評價指標進行評定，特別是Ⅺ度和Ⅻ度的評定需綜合考慮房屋震害和地表震害現象。郯城震例模型結果中Ⅺ度范圍主要集中于等震線Ⅻ度圈內，本文認為在綜合考慮史料記載和地質調查資料的基礎上，該地震可能存在Ⅻ度烈度區。

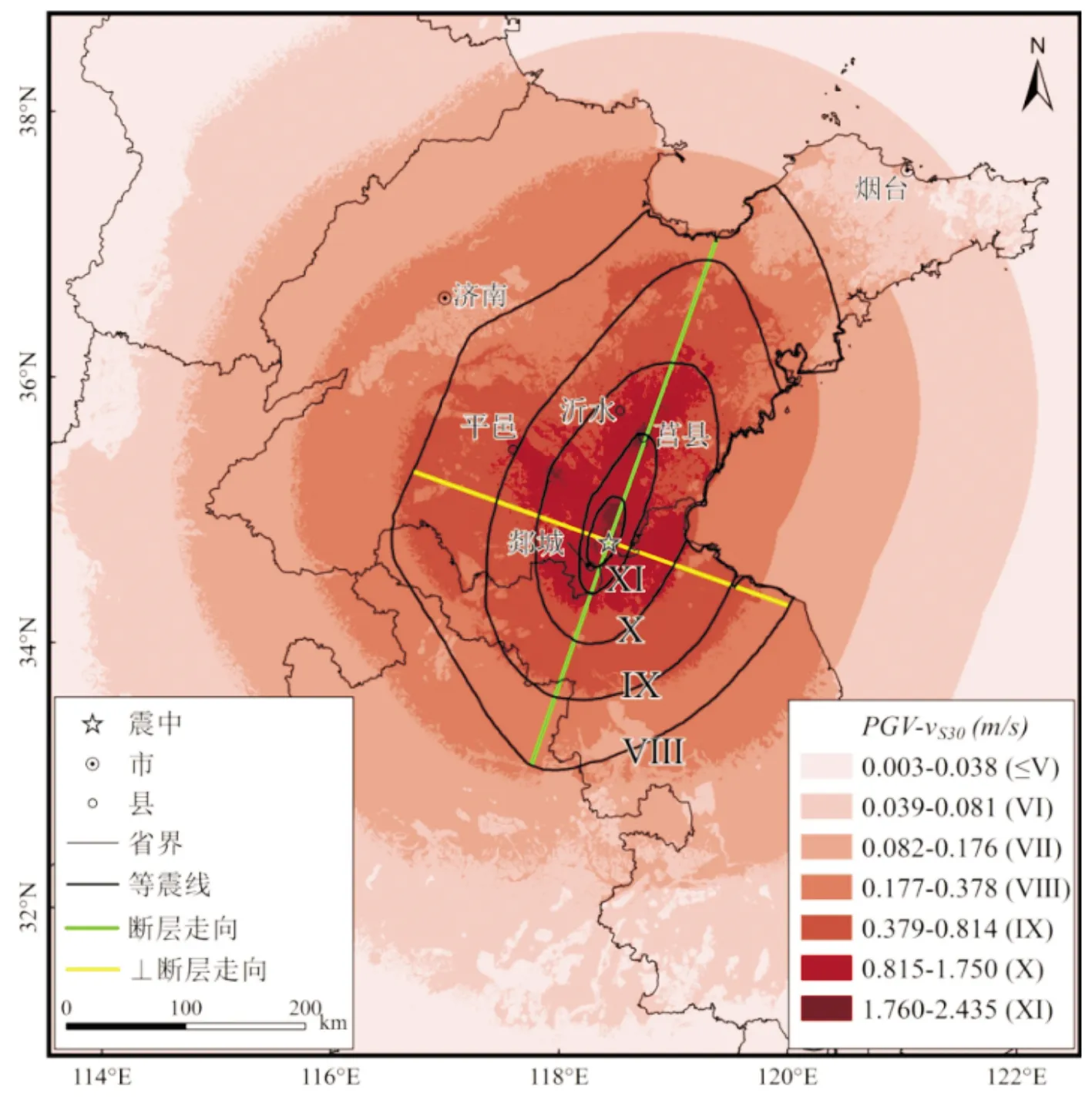
圖3 最佳模型結果

考慮地形放大效應計算的PGV-vS30結果展現了區域內地形對烈度的影響，濟南市南部山區和煙臺市大部分均為烈度異常區域，烈度值比周圍地區烈度低一度，可以為區域內的地震設防提供參考。沿圖3所示斷層走向和垂直斷層走向繪制剖面圖，結果見圖4，沿斷層走向計算結果與等震線變化趨勢總體一致，受地形影響模型結果走勢出現小距離內的變動，其最大值處對應等震線最大值，在莒縣附近也存在小范圍的高烈度區域，在垂直斷層走向，兩者的變化趨勢更相似。因此，本文認為“主震+強余震+最短斷層距”的數據方法組合是可靠的，可以為歷史地震烈度范圍和大小的評定提供參考。

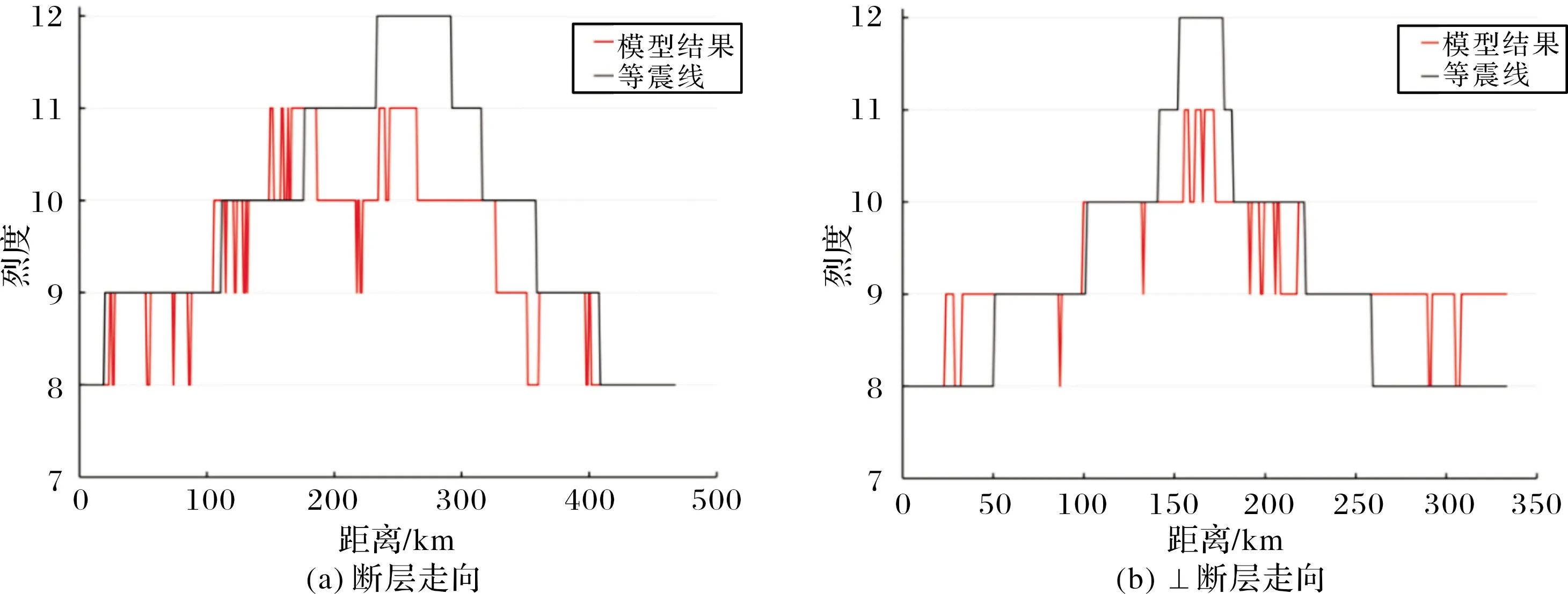
圖4 斷層走向和⊥斷層走向剖面圖

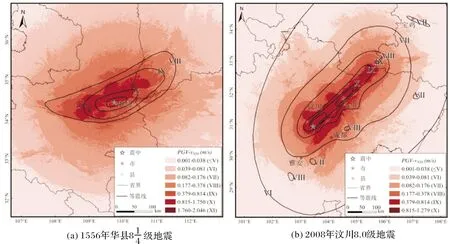
圖5 1556年陜西華縣地震和2008年汶川地震模型結果

3.4 其他震例驗證

4 結論與討論

本文討論了一種利用地震烈度衰減模型和余震數據推斷歷史大地震烈度的新方法，該方法計算簡單，僅需要歷史地震震級、位置、震源深度和余震位置信息便可計算，即使余震信息缺失，也可使用區域內經驗地表破裂公式推斷的地表破裂長度粗略評定烈度，該方法可以為歷史地震烈度范圍、震級大小的判定提供參考，在結合史料記載和地質調查資料等情況下能比較準確地判定烈度分布。模型考慮地形影響，計算結果展示了強震發生后震區內烈度的微觀差異，可以為區域內建筑設防、城市規劃、情景模擬提供新的數據參考。

最短斷層距模型適用于大地震烈度評估。文中以1668年郯城地震、1556年陜西華縣地震和2008年汶川地震為例對新方法進行討論和驗證，研究結果顯示采用“主震+強余震+最短斷層距”方法獲取的烈度圖范圍準確性較高、烈度值接近權威機構發布的烈度數值。因此，對于余震資料豐富的歷史大地震，我們建議選取沿斷層方向分布的強余震數據進行計算，并結合該震例史料和地質現象進行校正，繪制等震線圖。

強余震數據為地震烈度研究提供了比較豐富的信息，在今后的工作中還可以從以下幾個方面繼續完善該方法：校訂歷史上具有重大影響的大地震余震數據，特別是強余震震級和位置信息，進行歷史大地震強余震目錄整理；開展余震數據在現代大地震烈度評估中的應用研究；改進文中最短斷層距模型，分區域研究更精細的烈度衰減關系和VS30數據，提高不同區域內計算結果的精度等。