基于改進Apriori 算法的高校體測數據關聯分析①

蔣茜茜, 楊風暴, 楊童瑤, 張錦榮

(中北大學 信息與通信工程學院, 太原 030051)

信息社會產生的大量數據急需強有力的數據分析工具, 將數據轉換成有用的信息、知識, 因此, 數據挖掘技術[1]應運而生. 高校體測數據的關聯規則挖掘能直接反映項目集中數據的潛在關聯, 對幫助學生提高體能素質具有重要的意義.

張崇林等[2]通過體質測試數據處理方法分析, 認為體質測試數據適合進行關聯規則數據挖掘, 并且通過關聯規則數據挖掘, 發現了原知識體系利用BMI 和體脂率評價肥胖的矛盾現象, 可知Apriori 算法利用逐層迭代搜索的方法挖掘數據間的關聯關系, 是目前關聯規則應用最廣、最經典的算法. 趙常紅等[3]運用關聯規則的Apriori 算法并設置支持度、置信度, 分析男、女生的不同體測數據, 各測試指標等級數量分布情況及其之間的關聯性, 但是忽略了算法的運行效率. 劉辛等[4]提出一種基于數組的Apriori 算法, 減少了候選頻繁集冗余, 提高了Apriori 算法效率, 找出了各體測項目間的關聯關系, 但是忽略了遍歷數據庫的次數對運行效率的影響. 崔亮等[5]提出一種基于動態散列和事務壓縮的關聯規則挖掘算法, 通過估計產生候選項集的大小來動態選擇是否使用hash 技術, 并且利用事物壓縮技術刪除不包含頻繁項集的事務, 從而提高算法運行效率.

由上述文獻可知關聯規則Apriori 算法可應用于高校體測數據場景, 其弊端在于數據量增加到一定程度時算法效率低下[6]. 與崔亮等[5]提出的方法不同, 本文提出的基于事務壓縮和hash 技術的改進Apriori 算法, 無需估計產生候選項集的大小, 是根據體測數據特征有限并且長度一致的特點, 先使用散列技術壓縮要考察的候選項集, 再結合事務壓縮技術減少遍歷數據集的事務項數和長度, 將這兩種算法優勢完美結合, 從而大大提高算法的運行效率, 并且有效得到體測數據間的關聯, 能較好地預測影響學生體能素質的因素, 從而輔助指導學生的體能訓練.

1 基于事物壓縮和hash 技術的Apriori 關聯規則算法

關聯規則是描述數據事務特征屬性間的規律, 通過某些屬性來預測其他屬性的關聯. 在體測數據中, 設項集itemset={item_1,item_2, …,item_n}是高校學生體測數據特征屬性的集合,n是屬性的個數[7]. 一條學生體測數據是一個事務T, 一個事務T是一個項集, 每個事務均與一個唯一標識符Tid相聯系, 體測數據中學籍號是唯一的標識符Tid[8]. 不同學生的體測數據組成了事務集D, 它構成了關聯規則發現的事務數據庫.

用支持度和置信度衡量關聯規則的標準, 例如形如A?B的關聯規則, 體測數據屬性項A與屬性項B同時存在的概率即為該數據關聯規則的支持度Support(A?B); 體測數據屬性A存在的條件下, 屬性B也存在的概率即為體測數據關聯規則的置信度Confidence(A?B), 其分別如式(1)和式(2)表示.

1.1 Apriori 算法

Apriori 算法是利用k-項集來產生(k+1)-項集迭代的方法[9], 其操作流程如圖1, 設定最小支持度min_sup和最小置信度min_conf, 掃描整個數據庫, 統計長度為1 的每一項的個數, 篩選滿足最小支持度的項, 得到頻繁1-項集L1; 由L1自身連接生成候選2-項集C2, 得到的C2進行剪枝操作, 統計長度為2 的每一項的個數,刪除不滿足最小支持度的項, 得到頻繁2-項集L2, 如此迭代下去, 直到不能再找到頻繁k-項集[10], 最終得到頻繁項集L={L1,L2, …,Lk}.

圖1 經典Apriori 算法流程

Apriori 算法的弊端在于數據量增加到一定程度時算法效率低下, 具體表現在以下3 個方面:

1)在Lk-1與自身連接生成Ck過程中, 可能需要產生大量候選項集. 例如, 假設Lk-1中有m個k-項集,則在進行自身連接需要進行比較的時間復雜度為O(k×m2).

2) 在對Ck剪枝的過程中, 判斷Ck中任意一個k項候選集的(k-1)-項候子集是否為Lk-1的子集, 最快只需要掃描一次得出結果, 最慢需要k-1 次, 所以平均時間為|Ck|×|Lk-1|×k/2.

3)在篩選滿足最小支持度的候選項集過程中, 對Ck中的每個項進行計數, 需要掃描數據庫|Ck|次.

1.2 基于散列技術的Apriori 算法

散列技術又名hash 技術[11], 基于散列技術的Apriori算法的優勢主要體現在能將生成的Ck進行壓縮, 大大縮小了Ck占用空間. 首先, 掃描數據庫所有的事務得到C1, 篩選滿足最小支持度的候選項集得到L1; 然后利用散列技術來改進產生頻繁2-項集的方法, 具體如下: 將每條事務生成其所有的2-項集并且運用散列技術構造散列函數把它散列到相應的散列表中, 即分配到不同的桶中并計數, 而且相同的數據項被分配到同一存儲空間, 且對應著同一計數器, 只需計數加一即可,且降低了所需的存儲空間. 同樣的生成頻繁k-項集也是用相同的方法, 并且在散列表中可以篩選出容器計數小于支持度閾值的k-項集, 因此可以很好的對要檢測的k-項集執行壓縮操作.

散列技術的缺點是其運行效率依賴于事務的平均長度, 也就是說如果數據集的特征少, 平均長度短, 其運行效率就高, 反之運行效果差. 而Apriori 方法運行效率不依賴于數據集特征的長度和數量, 所以一定程度上彌補hash 技術的缺點, 兩者互補可以大大增加算法的運行效率.

1.3 基于事務壓縮技術的Apriori 算法

基于事務壓縮技術的Apriori 算法的優勢主要體現在將進一步迭代掃描的數據庫進行壓縮, 進而影響掃描事務庫的次數, 增加算法的運行效率[12]. 該技術的改進是根據經典Apriori 算法的性質, 即如果一個事務不包含任何的頻繁k-項集, 則其也不包含任何的頻繁(k+1)-項集. 因此在生成Lj(j＞k)時, 遇到上述事務時,可以加上標記或刪除, 掃描數據庫時不需要再掃描該事務, 減少掃描事務庫的次數.

1.4 基于散列技術和事務壓縮相結合的改進

根據以上了解可知, 基于散列技術的改進和基于事務壓縮技術作用于Apriori 算法過程中的不同部分,基于散列技術的改進體現在減少候選項集的規模, 并更進一步減少數據庫掃描的次數, 而事務壓縮技術能夠逐漸減小數據庫中事務的長度和規模, 都主要作用在Apriori 算法的剪枝部分[13], 并且兩者會促進對方的效果, 而不產生負面影響.

改進算法流程如算法1 所示, 根據高校體測數據的特征有限和并且長度一致的特點, 利用散列技術遍歷一次事務集, 即可生成頻繁項集L1,L2,L3, 再利用事務壓縮技術由L3生成L4, 如此迭代下去, 直到不能再找到頻繁k-項集. 因為迭代生成候選項時可能性太多,數據量大時占用內存太大, 所以不繼續使用hash 技術繼續生成L4, 而改用事務壓縮技術, 有效地避免hash技術的短板.

算法1. 改進Apriori 算法輸入: 數據庫D, 最小支持度min_sup, 最小置信度min_conf過程:1)掃描數據庫, 利用散列技術生成頻繁1-項集L1, 頻繁2-項集L2, 頻繁3-項集L3;2)通過頻繁項集Lk-1 自身連接生成Ck 候選項集, 再進行剪枝;3)利用事務壓縮技術減少掃描事務集的次數, 刪除不滿足最小支持度的項集, 生成頻繁k-項集Lk;4)對k＞3, 重復執行步驟2)和3), 判斷頻繁k-項集的長度, 如果為0,則跳出循環, 得到最終結果頻繁項集L, 否則返回步驟2);5)篩選出滿足min_sup 和min_conf 的頻繁項集即強關聯規則, 結束.輸出: 強關聯規則

2 實驗過程及分析

2.1 數據準備

以我校2016 級7 709 名大學生第一學年的體測成績為實驗對象, 從數據庫中提取與體測成績有關的數據, 如: 學籍號、性別、身高、體重、肺活量、50 m、立定跳遠、1 000 m (男生)、800 m (女生)、引體向上(男生)、仰臥起坐(女生)共11 個屬性, 表1 是以學籍號為主鍵的體測成績.

表1 學生2016 年的體測成績

2.2 數據清洗及轉換

實驗數據來源于我校體測中心, 所以得到的數據較為規范, 但是數據中存在部分學生體測成績缺項, 又考慮到部分特殊學生免測的情況, 所以要對原始數據先進行預處理, 經過數據清洗、數據轉換和數據消減,實現算法在高校學生體測中的應用.

數據清洗的實際操作主要有:

(1)針對缺項數據, 如果缺項數據較多則刪除該學生的體測成績[12]; 如果缺項較少, 則可以通過求該項目成績的平均值、眾數或者中位數填充;

(2)針對免考學生的數據, 由于各項成績為缺項,可以直接刪除, 使得清洗后的數據標準、干凈且連續.

數據轉換將不同標準的連續型數據轉換成標準相同的離散型數據, 便于后續的統一處理. 雖然體測項目間的評判標準不同, 但是都可以劃分為A、B、C、D 四個等級, 即優秀、良好、及格、不及格, 其次, 為了方便統計以及提高數據挖掘的效率, 用數字1 和2分別代替性別的男和女, 用小寫字母開頭代替各項目的名稱, 如: 肺活量用fhl 代替.

數據轉換結果如表2 所示, 經過數據清洗及轉換得到的標準數據最終有7 337 條.

表2 數據轉換結果

2.3 數據消減

數據消減是在保持數據庫的完整性的情況下, 從上述數據集中獲得精簡的數據集, 能夠保證不影響最終的算法結果. 男生和女生體測項目和評價標準有所不同, 所以本文將在數據挖掘時對男生和女生的體測成績數據分別進行處理. 數據消減就是針對數據庫中篩選出的男生、女生的體測數據, 消除與體測項目屬性無關的項, 例如學籍號, 性別.

2.4 實驗驗證

試驗環境為Intel(R) Core(TM) i5-5200U 2.20 GHz處理器, 4 GB 內存, 操作系統為Windows 10, 算法在Python 3.8 下實現.

設定min_conf= 0.9, 設置不同的最小支持度, 利用Apriori 算法以及本文提出的事務壓縮和hash 結合的算法得到的結果如表3 所示, 在相同的最小支持度下得到的關聯規則數目相同, 表示改進后的算法確保了Apriori 算法的準確性, 由此可以得到改進算法的可靠性; 隨著最小支持度的增加, 改進后的算法執行效率大大提高. 改進后的算法在保證挖掘精度的同時提高算法效率.

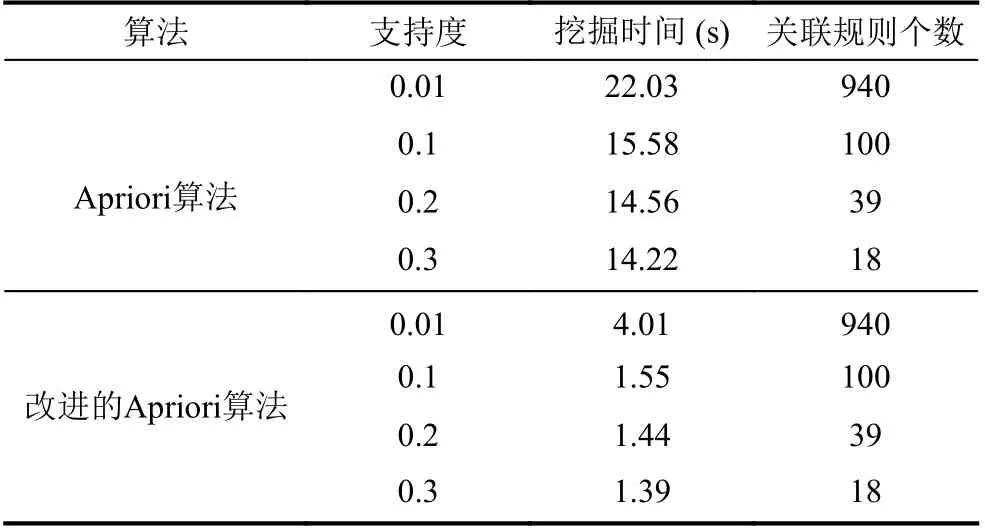
表3 兩種算法比較

為了能直觀地反映出改進后的算法運行效率更高,在設置不同最小置信度、最小支持度情況下, 將得出的實現數據進行分析對比, 結果如圖2 和圖3 所示. 圖中結果可知, 本文提出的改進算法效率明顯優于經典Apriori 算法、基于hash 的Apriori 算法以及基于事物壓縮的Apriori 算法. Apriori 算法和基于事物壓縮的Apriori 算法隨著支持度和置信度的增加執行效率比較接近, 其中基于事物壓縮的Apriori 算法效率稍高; 基于hash 改進算法相較于Apriori 算法和基于事物壓縮的Apriori 算法本身具有一定的優越性, 本文將hash技術與事務壓縮技術相結合得到了更好的效果.

圖2 不同支持度性能對比

圖3 不同置信度性能對比

2.5 結果分析

原始的體測數據經過數據預處理后得到2 266 條女生體測數據和5 071 條男生體測數據, 設置最小置信度min_conf= 0.9, 最小支持度min_sup= 0.3, 將這兩類數據分別用文中提到的4 種算法進行關聯規則挖掘,將各運行效率進行比較, 如表4 所示, 可以看出本文提出的基于事物壓縮和hash 結合的算法執行效率更高,與經典Apriori 算法執行效率相比, 女生體測數據算法執行效率提高了86.12%, 男生提高了90.63%; 與基于事物壓縮的Apriori 算法相比, 女生體測數據算法執行效率提高了80.57%, 男生提高了89.32%; 與基于hash 的Apriori 算法相比, 女生體測數據算法執行效率提高了48.1%, 男生提高了55.69%; 可見, 該4 種算法應用于男生的體測數據的執行效率比女生更高, 說明數據集量越大改善效果越明顯.

表4 4 種算法執行效率比較 (s)

表5 和表6 分別是男生和女生體測成績的關聯規則挖掘結果, 由表5 可以看出挖掘出的男生第一條關聯規則50 m:C ?ytxs:D, 支持度為72.1%, 置信度為93.5%, 說明男生50 m 成績如果是C 等級, 那么他的引體向上的成績為D 等級的可能性為93.5%, 而這種事件發生的可能性為72.1%, 可知此學生的50 m 成績可以預測其引體向上的成績, 以此類推. 可通過某學生的歷史數據來預測其他成績的及格情況, 達到預警的效果, 使該學生加強某方面的鍛煉, 進行有針對性的體能訓練, 幫助老師安排訓練計劃有著指導性的意義.

表5 關聯規則 (男生)

表6 關聯規則 (女生)

3 結論與展望

現在數據挖掘技術已經非常成熟, 然而數據挖掘和體能分析結合的應用卻很少, 本文通過對比4 種算法實現的結果和執行效率, 表明改進后的算法在高校學生體測中的應用具有一定的可靠性和有效性, 對于比較大的數據集效率改善更明顯. 并且將本文所提出的算法, 與經典Apriori 算法相比, 可知執行效率提高了85%以上, 并且挖掘出體測成績間的潛在關聯, 分析身體素質的不足之處, 對學生重視體育鍛煉, 輔導老師安排學生的訓練計劃具有指導性的意義.