低熱值氣雙層多孔介質穩燃特性數值模擬

周仁杰，張杰，王玉嬌，王銀峰

(南京工業大學能源科學與工程學院， 南京 211816)

1 研究背景

瓦斯(主要成分為CH4)作為僅次于CO2的第二大溫室氣體，排放量約占全球溫室氣體排放總量的20%。大氣中CH4的濃度遠低于CO2，但CH4溫室潛能指數是等量CO2的25倍。按照世界增溫潛勢計算，2018年煤炭、石油能源行業的CH4排放相當于1.0×1010t CO2，能源行業CH4減排對于保護環境具有重要意義。當前，低濃度(6%～30%)煤礦瓦斯的利用率僅約28 %，發展低濃度瓦斯利用技術具有重要的意義。根據氣體燃料自身的低位熱值可將氣體燃料分為高熱值氣體(>15.07 MJ/Nm3)、中熱值氣體(6.28～15.07 MJ/Nm3)和低熱值氣體(<6.28 MJ/Nm3)，其中低熱值氣體具有燃燒穩定性差、易熄滅和易吹脫等特點[1]。多孔介質燃燒技術能夠高效穩定的燃燒低熱值氣體，具有溫度分布均勻，輻射熱效率高和燃燒穩定性好等一系列優點，受到越來越多研究者的關注。

PEREIRA[2]等人研究了預混合氣體在多孔介質中燃燒和自由空間中燃燒的狀況，發現在多孔介質中燃燒擁有更高的燃燒溫度，而且燃燒溫度與修正Lewis數、當量導熱系數和孔隙率有關。XU[3]模擬了微尺度多孔介質燃燒器，通過回熱裝置設置，解決了微尺度燃燒器難以自維持火焰的難題。LIU[4]等研究表明火焰能否在多孔介質表面進行燃燒取決于瞬時氣體流速與局部火焰傳播速度之間的動態平衡關系。SONG[5]等人對甲烷在不同排列多孔介質中的燃燒進行數值模擬研究，發現多孔介質的排列方式會顯著影響火焰穩定極限。BUCKMASTER[6]等人發現氣體流量會影響火焰的穩定性與火焰面的位置。AKBARI[7]等人對多孔介質燃燒器中的預混合燃燒進行了數值研究，發現當量比增加時燃燒器的穩燃范圍擴大。

此外，雙層多孔介質結構有助于提高火焰在多孔介質中燃燒的穩定性。HSU[8]等人發現火焰可以有效穩定在兩個不同孔隙率的陶瓷塊之間或其附近。KUIKARNI[9]等人研究表明，兩段多孔燃燒器的上游部分應具有低導熱系數、低對流換熱系數、低孔隙率、短長度以及高輻射衰減系數；而下游部分應具有高導熱系數、高對流換熱系數和中等輻射衰減系數。MISHRA[10]研究了雙層多孔介質內的預混燃燒和氣固之間換熱，結果表明較小的孔特征長度意味著較高的體積對流換熱系數，在更短的時間內即可達到熱平衡。HUANG[11]等人數值模擬了低熱值氣體在填充顆粒型雙層多孔介質燃燒器中的燃燒特性，表明上游對流換熱系數對燃燒性能的影響較大。GAO[12]等人研究了沼氣在填充顆粒的雙層多孔介質燃燒器中的燃燒，發現隨著CO2含量的增加，火焰穩定極限降低。

目前對于多孔介質中的燃燒模擬，研究的對象多以純燃料為主，并且多采用規則的固體顆粒堆積而成的多孔介質燃燒器。泡沫型多孔介質作為一種重要的多孔介質，其擁有更高的比表面積與孔隙率，因此有必要對低熱值氣體在泡沫型多孔介質燃燒器中的燃燒進行模擬研究。本文基于泡沫陶瓷單位體積的表面積計算公式對其壓力降系數[13]進行修正并選擇隨溫度變化的比熱容計算公式，依據Fluent軟件建立雙層多孔介質燃燒器二維穩態雙溫數學物理模型，通過改變低熱值燃氣當量比與流量，研究其穩燃流量極限、火焰面結構及溫度分布特征，獲得低熱值氣體在雙層多孔介質交界處的穩燃特性。

2 模型建立

2.1 物理模型建立

如圖1所示建立雙層多孔介質燃燒器的物理模型，燃料采用15 % CH4和85 % N2的混合氣，燃燒器圓筒內徑為52 mm，高為105 mm，內部填充兩層多孔介質分為預熱區和燃燒區。預熱區厚度45 mm內部填充60 ppi(每英寸孔數)，碳化硅泡沫陶瓷；燃燒區厚度60 mm內部填充10 ppi，碳化硅泡沫陶瓷。燃燒器內部填充的兩種多孔介質性質參數見表1[14]。

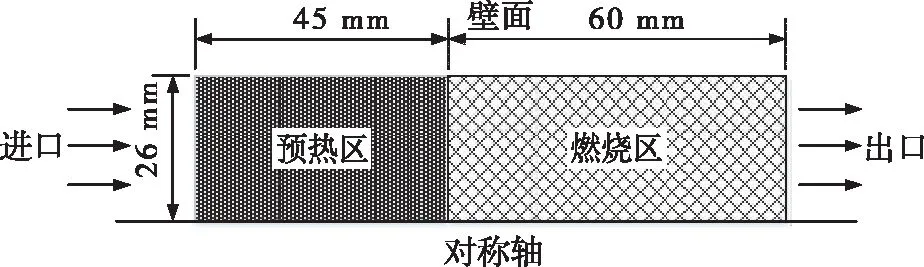
圖1 雙層多孔介質燃燒器的物理模型

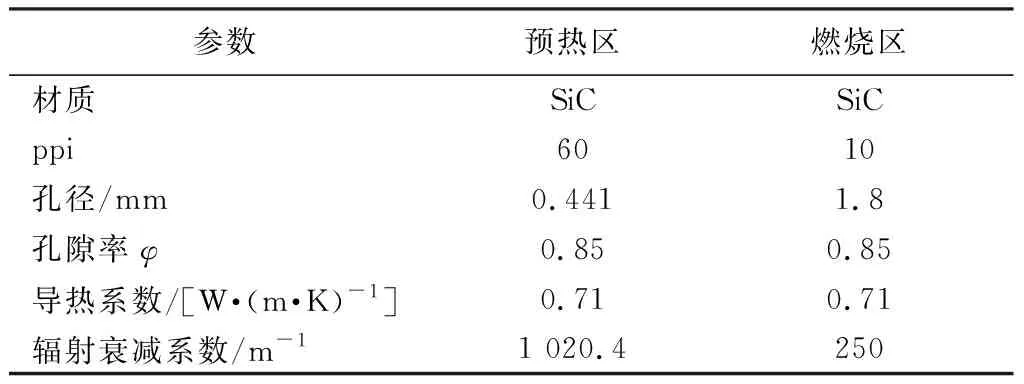
表1 多孔介質性質參數

2.2 簡化假設與控制方程

在建立數學模型時，根據實際特點進行如下假設：

1)預混氣體視為不可壓縮的理想氣體；

2)忽略氣固間輻射傳熱，多孔介質內部的固體輻射傳熱采用有效導熱近似；

3)燃燒室壁面無滑移，重力影響忽略不計；

4)多孔介質視為一種均勻的各向同性的材質，忽略多孔介質彌散效應；

5)采用甲烷-空氣兩步化學反應機理。

結合以上的基本假設，并采用體積平均法對自由空間內反應流的通用控制方程進行修改，得到多孔介質中燃燒模型的各個基本方程。

(1)連續性方程。

?·(φρgu)=0

(1)

式(1)中，φ為泡沫陶瓷多孔介質材料的孔隙率；ρg為氣體密度，kg/m3；u是氣體速度矢量，m/s。

(2)動量守恒方程。

?·(φρguu)=-φ?p+?·(φτ)+Si

(2)

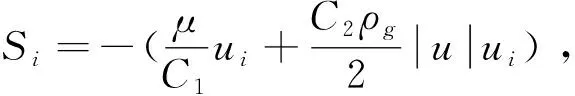
(3)

式(3)中，φ為孔隙率；Sv為泡沫陶瓷單位體積的表面積；dp表示為壓力差，Pa；L表示為長度，m；α和β值根據RICHARDSON[16]等人給出的實驗關系式確定：

(4)

(5)

式(5)中，dm為多孔介質孔徑。

(3)組分守恒方程。

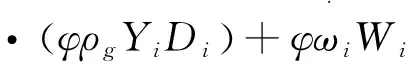
(6)

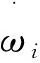
(4)能量守恒方程。

Fluent中嵌入的多孔介質燃燒模型分為熱平衡模型和非熱平衡模型，對應于單溫模型和雙溫模型。單溫模型認為燃燒時氣體溫度和固體溫度相等，處于熱平衡狀態。而雙溫模型認為預混氣體在多孔介質中燃燒時氣體燃燒和多孔介質固體間有一定的溫差。由于預混氣體在多孔介質內燃燒時氣固溫度不同，且氣固間存在強烈的對流換熱，因此需要在Fluent中啟用非熱平衡模型并對其加以修改。

1)氣體能量方程。

?·[φu(ρgCgTg+p)]=?·(λeff-g·?Tg)-

(7)

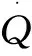
(8)

式(8)中，λg是氣體混合物的導熱系數；DT,i為熱擴散系數，根據如下經驗系數組成的關系式進行計算[18]：

DT,i=-2.59×10-7

(9)

式(9)中，hv為多孔介質固體骨架與氣體間的體積對流換熱系數，根據如下公式進行計算[19]：

Nu=CRem

(10)

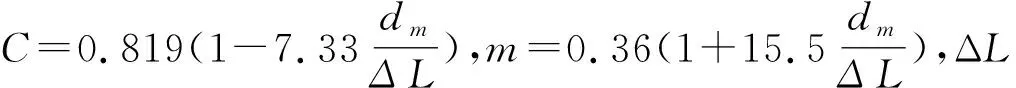
2)固體能量方程。

?·(λeff-s·?Ts)+hv(Tg-Ts)=0

(11)

式(11)中，λeff-s為固體多孔介質的有效導熱系數，λeff-s=(1-φ)λs+λrad，λs是多孔介質的導熱系數，λrad是多孔介質燃燒器內通過ROSSELAND擴散近似法得到的泡沫陶瓷的輻射換熱系數，可以通過下面表達式進行計算[20]：

(12)

式(12)中，σ為斯特藩-玻爾茲曼常數，σ=5.67×10-8W/(m2·K4)，βs為多孔介質輻射衰減系數；Ts為固體溫度，K；Cp為多孔介質固體定壓比熱容，J/(kg·K)，根據如下公式計算[21]：

Cp=25(20.558 59+64.579 62Ts,1-

Cp=25(46.902 22+5.845 968Ts,1-

(13)

(5)不可壓縮理想氣體狀態方程。

(14)

式(14)中，pop為操作壓力，pop=101 325 Pa；R為理想氣體常數，R=8.314 J/(mol·K)；Mw為氣體相對分子質量。

(6)輻射熱效率。

定義燃燒器出口輻射熱效率為燃燒器出口端的熱輻射功率與預混氣的輸入功率的比值，計算公式如下[22]：

(15)

式(15)中，分母為燃燒器熱負荷，VCH4為預混氣體中CH4流量，m3；LHV為甲烷的熱值，取為35.9 MJ/m3；Qout為燃燒器出口向外的輻射傳熱量：

(16)

式(16)中，A為燃燒器出口截面積，m2；ε為碳化硅泡沫陶瓷表面的法向發射率，取0.9；σ為玻爾茲曼常量，其值為5.67×10-8W/(m2·K4)；Ts,out為燃燒器出口端表面溫度，K；T0為環境溫度，K。

2.3 邊界條件與模型設置

入口邊界條件：

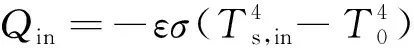
(17)

進口當量比區間0.45～0.7，當量比步長取0.05；流量區間取4.4～26.4 L/min，流量步長取2.2 L/min；當量比φ根據如下公式進行計算：

(18)

式(18)中，VCH4和Vair分別為甲烷和空氣相應的體積流量，L/min。

出口邊界條件：

(19)

假設燃燒器出口的變量梯度均為0。

壁面處邊界條件：

Qwall=-hwall(Ts,wall-T0)

(20)

假設固體壁面為無滑移邊界條件，壁面散熱系數hwall=5 W/(m2·K)。

在求解過程中，采用組分輸運的層流有限速率模型求解燃燒反應過程，使用甲烷空氣兩步反應機理；混合物的密度按不可壓縮理想氣體定律計算，比熱容按混合定律計算，動力粘度和導熱系數按各個組分的質量加權平均計算，質量擴散率和熱擴散系數按分子運動論計算；各個組分的比熱容按溫度的分段多項式進行計算，動力粘度和導熱系數按分子運動論計算；模型中求解方法采用Coupled算法，離散格式采用二階迎風格式，解的收斂程度根據控制方程殘差值來判斷，連續性方程殘差取值為10-5，其余為10-6。

3 結果與討論

3.1 穩燃范圍

當火焰面處于穩態時，火焰速度等于預混氣體在多孔介質內部的流動速度。火焰穩燃流量極限定義為在給定當量比下，多孔介質內部火焰能夠維持的最大和最小火焰速度，低于穩燃流量下限，火焰將發生回火或者熄滅，高于穩燃流量上限，將發生火焰的吹脫，圖2為不同當量比下火焰的穩燃流量極限。由圖2可以看出：預混氣體當量比小于0.5時，火焰不能夠在多孔介質中燃燒；預混氣體當量比大于0.5時，在一定的流量區間內燃燒能夠穩定在雙層多孔介質的交界面處，當流量低于穩燃的流量下限，火焰將在預熱區內燃燒或者發生熄滅，當流量高于穩燃的流量上限，火焰將被逐漸沖出多孔介質；隨著當量比的增加火焰穩燃的流量范圍也相應增加，火焰穩燃的流量上限由13.2 L/min增加到24.2 L/min；下限由8.8 L/min增加到11 L/min。原因是隨著當量比的增加，火焰的燃燒條件逐漸改善，因此火焰速度也隨之增加，火焰面呈現向上游進口方向移動的趨勢，為保持火焰面的穩定，此時需要更高的氣體流量才能夠防止火焰回火，同時由于火焰速度的增加，需要更高的氣體流量才能夠使得火焰面向下游出口方向移動，發生火焰的吹脫。此外還可以發現：當量比對火焰穩燃流量上限的影響較大，而火焰穩燃流量下限隨當量比的變化幅度相對較小。

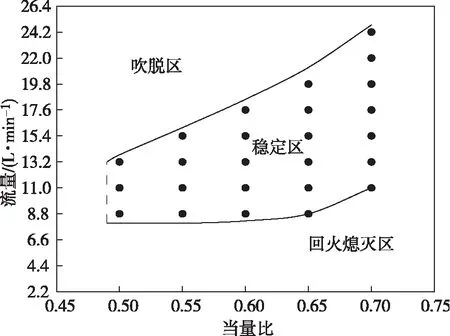
圖2 不同當量比下火焰穩燃流量極限

3.2 溫度分布特性

圖3為氣體不同當量比與流量下燃燒器內部的氣相溫度分布云圖。由圖3可以看出：三種工況下火焰面均能穩定在雙層多孔介質的交界面處，火焰面呈現為較薄的平面火焰。這是由于在預熱區輻射衰減系數較高，相對于燃燒區多孔介質導熱能力較弱，因而熱量回流能力較弱，使得火焰呈現往下游方向移動的趨勢；而在燃燒區輻射衰減系數較低，多孔介質導熱能力較強使得熱量回流能力較強，火焰面呈現往上游方向移動的趨勢，因此在兩種趨勢相互作用下火焰能夠穩定在雙層多孔介質的交界面處。此外還可以發現：當量比為0.5、流量為11 L/min和當量比為0.7、流量為24.2 L/min時，預熱區多孔介質中心溫度較低而邊緣溫度較高，當量比為0.7、流量為11 L/min，預熱區多孔介質中心溫度較高而邊緣溫度較低。這主要是由于當量比為0.7、流量為11 L/min的工況接近穩燃的流量下限，氣體被多孔介質充分預熱，即將發生火焰的回火。氣體不同當量比與流量下燃燒器沿中軸線的氣固溫度分布見圖4。

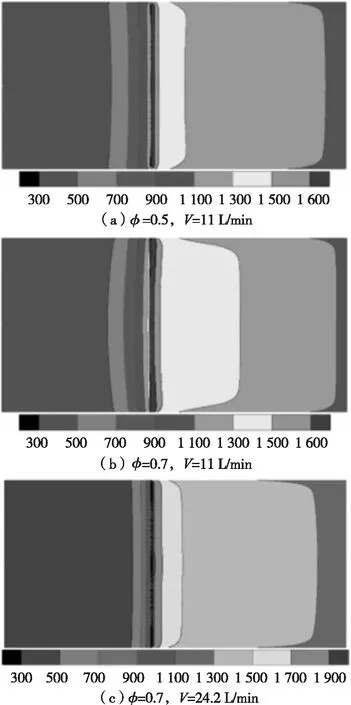
圖3 不同工況下燃燒器內部氣相溫度分布云圖

從圖4中可以看出：隨著燃燒器熱負荷的增加，使得燃燒產生的熱量不能夠及時傳遞給多孔介質，火焰面處氣固溫差逐漸由466 K增加到674 K；在燃燒區氣體溫度高于固體溫度，而在預熱區固體溫度高于氣體溫度，并且在靠近火焰面的區域多孔介質溫度梯度較大。這是由于多孔介質燃燒獨特的熱量回流機制：燃燒放出的熱量，使得火焰面后燃燒區的氣體溫度高于固體溫度，形成對高溫氣體的散熱作用，降低燃燒的峰值溫度；而又因為固體多孔材料較好的導熱能力，使得火焰面前預熱區的固體溫度高于氣體溫度，形成對低溫氣體的預熱作用，提高了氣體的火焰燃燒速度。此外還可以發現：在燃燒區沿著燃燒器軸線方向氣固溫差呈現先減小后增加的趨勢，最低可減少到8 K的溫差；在燃燒器出口由于與外界環境直接的輻射傳熱，氣體和固體溫度下降幅度增加，其中固體溫度下降幅度更大，出口處氣固溫差為73～107 K。

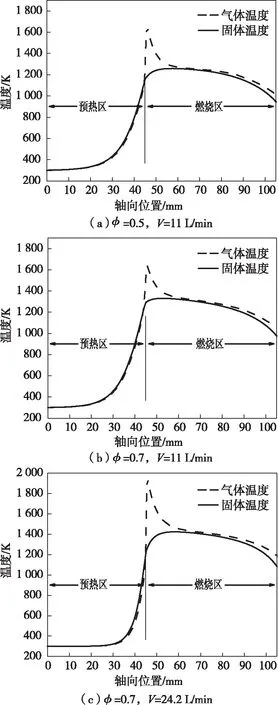
圖4 氣體不同當量比與流量下燃燒器沿中軸線的氣固溫度分布

3.3 燃燒輻射熱效率

不同當量比下燃燒器出口溫度與輻射熱效率隨氣體流量的變化關系見圖5。由圖5可以看出：隨著氣體當量比與流量的增加，燃燒器的熱輸入逐漸增加，燃燒器出口溫度由925 K升至1 085 K，但是輻射熱效率呈現逐漸下降趨勢由38.4 %降低至20.9 %，輻射熱效率最高可達38.4%。這是由于隨著燃燒器熱輸入的增加，燃燒產生的熱量不能夠及時傳遞給多孔介質，燃燒器散熱損失(排煙損失以及壁面散熱損失)所占的比例逐漸增加，使得燃燒器的熱效率逐漸降低。因此，在設計多孔介質輻射燃燒器時，合理選擇氣體流量，較低的氣體流量，擁有較高的輻射熱效率，但是輻射溫度較低；較高的氣體流量，擁有較高的輻射溫度，但是輻射熱效率偏低。

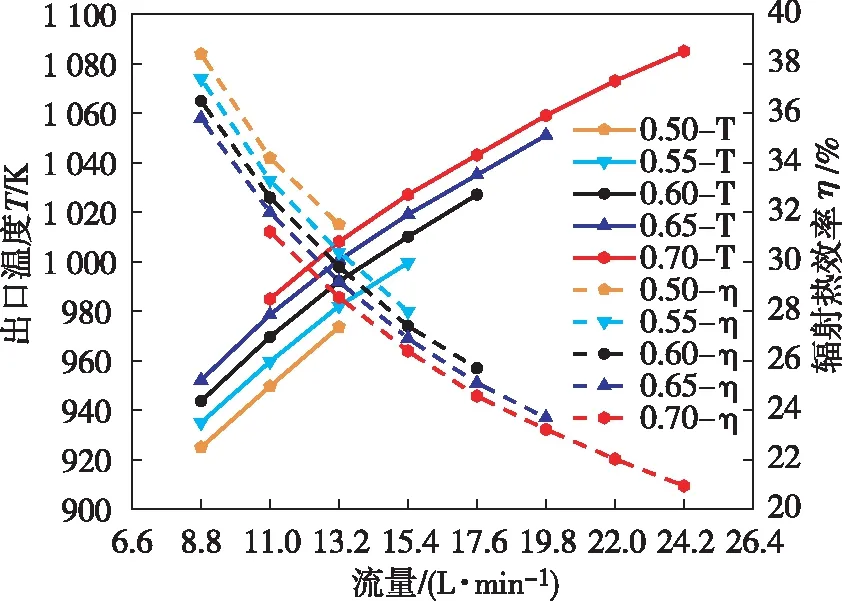
圖5 不同當量比下燃燒器出口溫度與輻射熱效率隨氣體流量的變化關系

4 結語

本文構建了適用于低熱值氣體的雙層多孔介質燃燒模型，對不同當量比與流量下的工況進行數值模擬研究，主要結論如下：

(1)當量比一定時，在一定流量范圍內燃燒能夠穩定在雙層多孔介質的交界面處，燃燒的最低當量比可達到0.5；隨著當量比的增加，火焰穩燃的流量上下限均增加，且火焰穩燃的流量區間也相應增大。

(2)當燃燒穩定在雙層多孔介質的交界面時，火焰為較薄的平面火焰；在火焰面處存在466～674 K的氣固溫差，沿著氣流方向氣固溫差呈現先減小后增加的趨勢，最低可減少到8 K的溫差，出口處氣固溫差為73～107 K。

(3)隨著氣體當量比與流量的增加，燃燒器的熱輸入逐漸增加，燃燒器出口溫度由925 K升至1 085 K，而輻射熱效率由38.4 %降至20.9 %。