基于雙層動態網絡的語言競爭微觀仿真模型
王志萍 畢貴紅 張壽明* 曾振華
1(昆明理工大學信息工程與自動化學院 云南 昆明 650500) 2(昆明理工大學電力工程學院 云南 昆明 650500) 3(中國人民銀行岳陽市中心支行 湖南 岳陽 414000)
0 引 言
目前,96%的人口使用大約4%的語言,而25%的語言使用者不到1 000人[1]。此外,語言學家估計,除非目前的趨勢發生變化,否則到本世紀末,目前所說的約6 000種語言中有90%可能會面臨瀕危甚至消亡[2]。
通過構建語言演化的模型來研究語言瀕危和調控的機理是目前常用的方法,目前研究語言演化問題計算模型主要有宏觀建模和微觀建模兩種方法。Abrams等[3]提出基于微分方程的系統動力學方程(AS模型)描述兩種語言競爭與演化問題,語言競爭模型的動力學分析認為兩種語言共存不是一種系統演化的穩定狀態。Stauffer等[4]給出了一種基于agent的微觀仿真模型(SAS模型),考慮了d維網絡上的系統演化特征,驗證了微觀仿真模型可以得到與宏觀建模方法相同的動力學特性。Castelló等[5]在Stauffer模型的基礎上進行了一定的擴展(CAS模型),模型引入雙語者agent和小世界網絡結構。研究認為小世界網絡結構和雙語者的引入并不能保證語言競爭系統中語言的多樣性,反而加速了語言單一化進程。Minett等[6]同樣給出了考慮雙語者和社會網絡的微觀AS改進模型(MWAS模型),模型中的社會網絡結構包括全連接網絡和局域世界網絡兩種,并利用語言地位作為調控政策措施來分析系統演化趨勢。曾振華等[7]在CAS模型和MWAS模型的基礎上引入語言的內部詞匯結構和社會圈子動態網絡,給出一種新的動態微觀語言競爭傳播與政策調控的社會仿真模型(ZAS模型)。研究了在不同社會開放程度等條件下語言地位作為調控政策的動力學特性。
上述這些研究使語言競爭的動力學機制越來越完善,更接近實際,但是與社會語言學家的理論研究和實際調查研究還有較大的脫節,甚至有矛盾,主要體現在以下幾個方面:(1) 社會網絡的影響。實際研究表明,強連接關系社會網絡有利于弱勢語言的保存,弱連接關系的社會網絡不利于弱勢語言的保存[8]。由于交通和通信的便利、城鎮化的加速,人們的社會網絡結構也在發生著變化,跨區域遠距離流動和通信聯系成為常態,人們的社會關系范圍擴大、強度弱化,這樣的社會網絡對語言保持提出了重要挑戰,構建的語言競爭網絡社會網絡模型應該考慮弱連接關系。(2) 語言地位和語言態度的影響。人們傾向于選擇語言地位高的語言學習,同時傾向于選擇語言交流網絡中多數人使用的語言學習。之前的研究者主要基于以上兩點來構造語言演化模型,并且大多以語言地位作為可改變的政策調控參數。近年來的研究表明,語言地位或語勢是短期內不可改變的,不適合作為可變的調控參數。陳保亞[9]認為,影響語言競爭的主要因素是語勢(即通常所指的語言地位),一種語言的語勢由該語言的使用人口數、詞匯量、擁有的文獻數量決定,所以語勢或語言地位很難在短期內改變,不能作為政策調控參數。鄧秋[10]指出語言態度是影響個人選擇語言行為的重要因素,可以通過教育等措施來改變,所以語言態度可以作為系統調控的參數。實際調研也表明,語言態度對語言保持有重要影響[11]。(3) 雙語教育的影響。雙語教育對于改善語言生態環境具有重要影響,有利于形成強有力的內部適應機制,這是改善和保護語言生態環境的最為有效措施[12]。教育是人們語言學習的三個途徑(社區、家庭或學校)之一,由于強調對強勢語言的單語教育,更加快了弱勢語言的消亡。雙語教育因素也是人們在語言保護中可以采取或改進的措施。
構建了新的社會網絡,網絡中既有社區內強連接關系,也有跨社區遠距離弱連接關系。在個體語言水平和垂直傳播模型中同時考慮了語言地位、語言態度和網絡連接關系對語言學習和遺忘的影響。增加了以教師節點與學習者節點構成的星型教學網絡來開展雙語教學。研究語言態度和雙語教學作為調控政策條件下系統的語言競爭動力學特性,即在不同政策調控下系統的長期演化趨勢。
1 已有語言競爭模型及其動力學特性
語言競爭演化系統中以強勢語言單語者比例NX、弱勢語言單語者比例NY、雙語者比例NZ為系統演化的考察變量,來分析系統長期演化的動力學特性。系統的動力學機制是指在系統初始和政策調控條件下,X、Y、Z三種語言人口比例從時間t=0到t=∞系統演化的最終狀態(包括穩定和不穩定兩種均衡點)。在系統演化過程中NX+NY+NZ=1。理論上系統最多有四個均衡點:(1,0,0)對應于系統中只有單語者X;(0,1,0)對應于系統中只有單語者Y;(0,0,1)對應于系統中只有雙語者Z;(x,y,z)對應于系統中三種語言共存或者強勢語言和雙語共存。
AS模型[3]給出了兩種語言競爭的宏觀動力學模型。模型的分析結果與實際的瀕危語言案例中數據保持一致。模型的成功推動了社會計算方法在語言競爭問題中的應用。研究得到該模型的動力學特性為:系統的演化結果有兩個穩定均衡點(1,0)、(0,1),一個不穩定均衡點(x,y),不穩定均衡點會按一定概率遷移到穩定點。所以系統的演化結果表明兩種語言共存不是一種穩定態,系統最終只有一種語言在競爭中勝出。
CAS模型[5]構建了引入雙語者和社會網絡結構的微觀agent復雜網絡仿真模型。網絡中語言者節點agent有三種可能的狀態:單語X、Y及雙語Z。模型分析結果表明:系統有兩個穩定均衡點(1,0,0)和(0,1,0),一個系統不穩定均衡點為(x,y,z);系統不穩定均衡點的位置由系統的語言地位和初始人口比例決定;雙語者和小世界網絡社會結構不能改變系統最終演化結果,系統最終仍然只有一種語言保留。
MWAS模型[6]同樣在AS模型的基礎上引入雙語者和社會網絡結構(包括全連接網絡和局域世界網絡)構建了語言競爭微觀復雜agent網絡模型,模型以語言地位作為動態調控政策分析了語言競爭系統動力學特性。研究認為在無政策調控下系統的動力學特性與CAS結果相同,通過對系統演化過程中的語言地位進行動態調控可以使系統的不穩定點改變為穩定點,實現語言共存。
ZAS模型[7]采用兩個長度為F的二進制字串表達agent的語言內部結構,并引入社會圈子網絡給出一種新的動態微觀語言競爭社會仿真模型。計算實驗表明:給出的新模型具有與MWAS模型相同的動力學特性,在合適的時間窗口對語言地位實施動態調控可以將系統不穩定均衡點轉變為穩定均衡點,實現兩種語言共存。文獻[13]在此基礎上構建了具有整數字符串結構的復雜agent網絡微觀社會仿真模型。模型計算實驗結果表明新模型與ZAS模型具有相同的動力學特性和調控機制,同時具有更豐富的表達能力。
2 新型語言競爭傳播模型
2.1 語言競爭傳播網絡
2.1.1社會圈子網絡生成原理
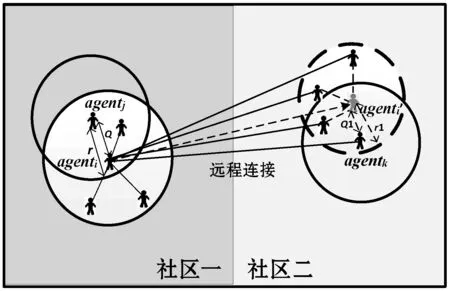
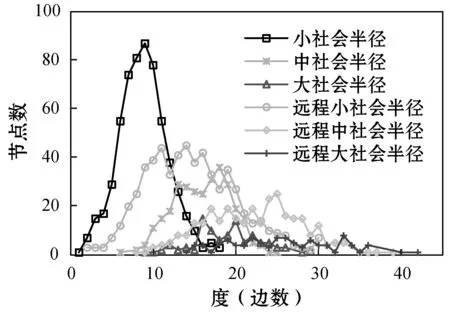
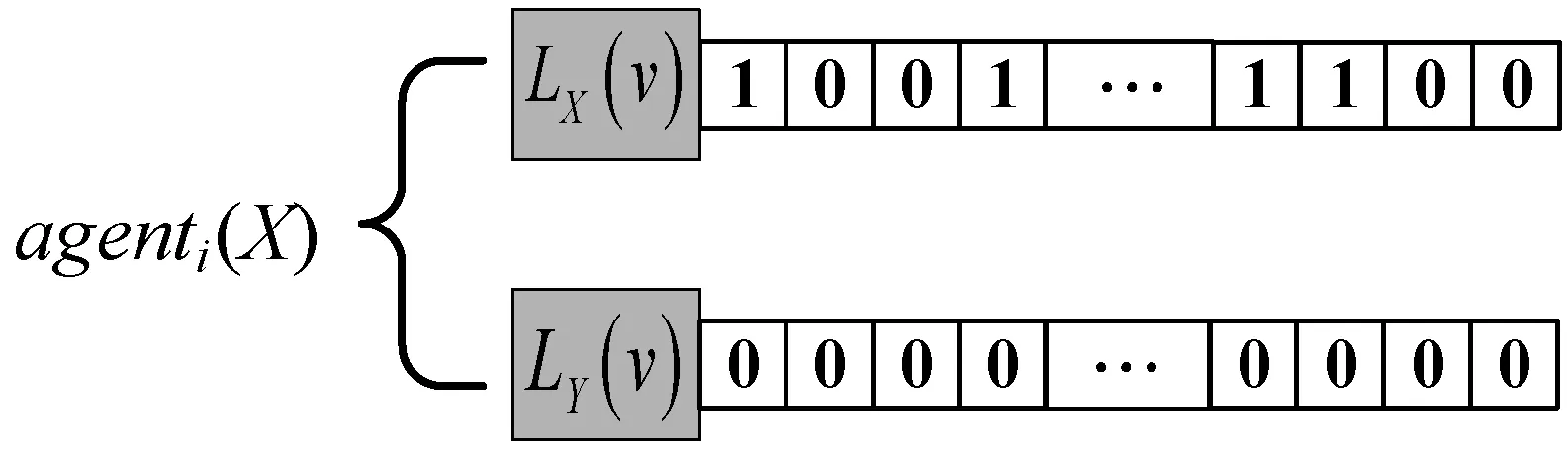
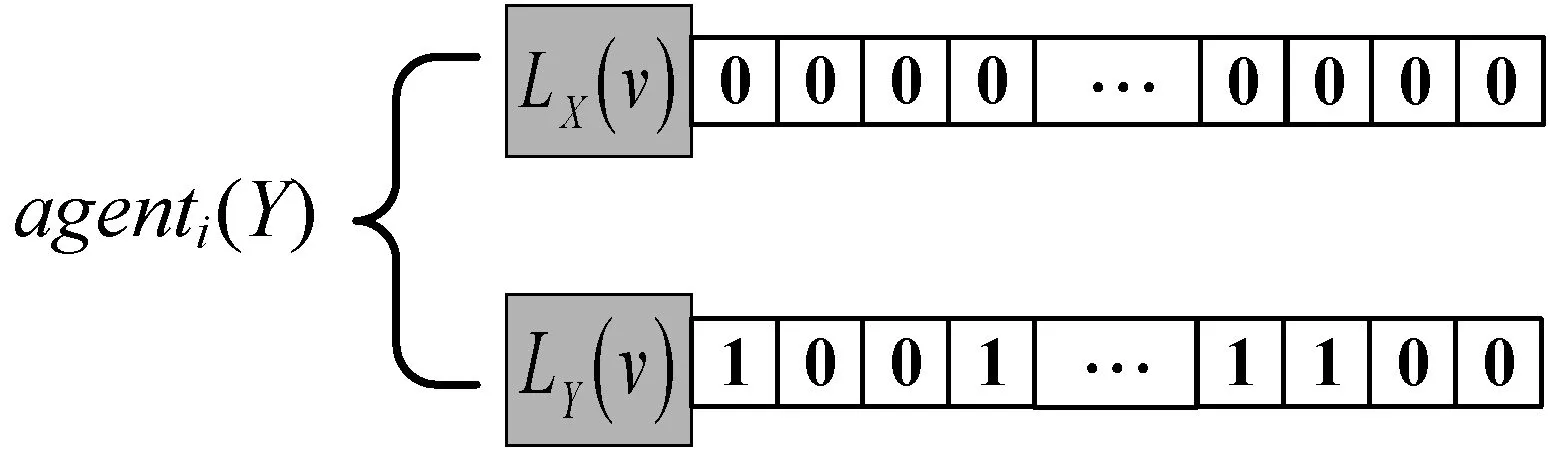
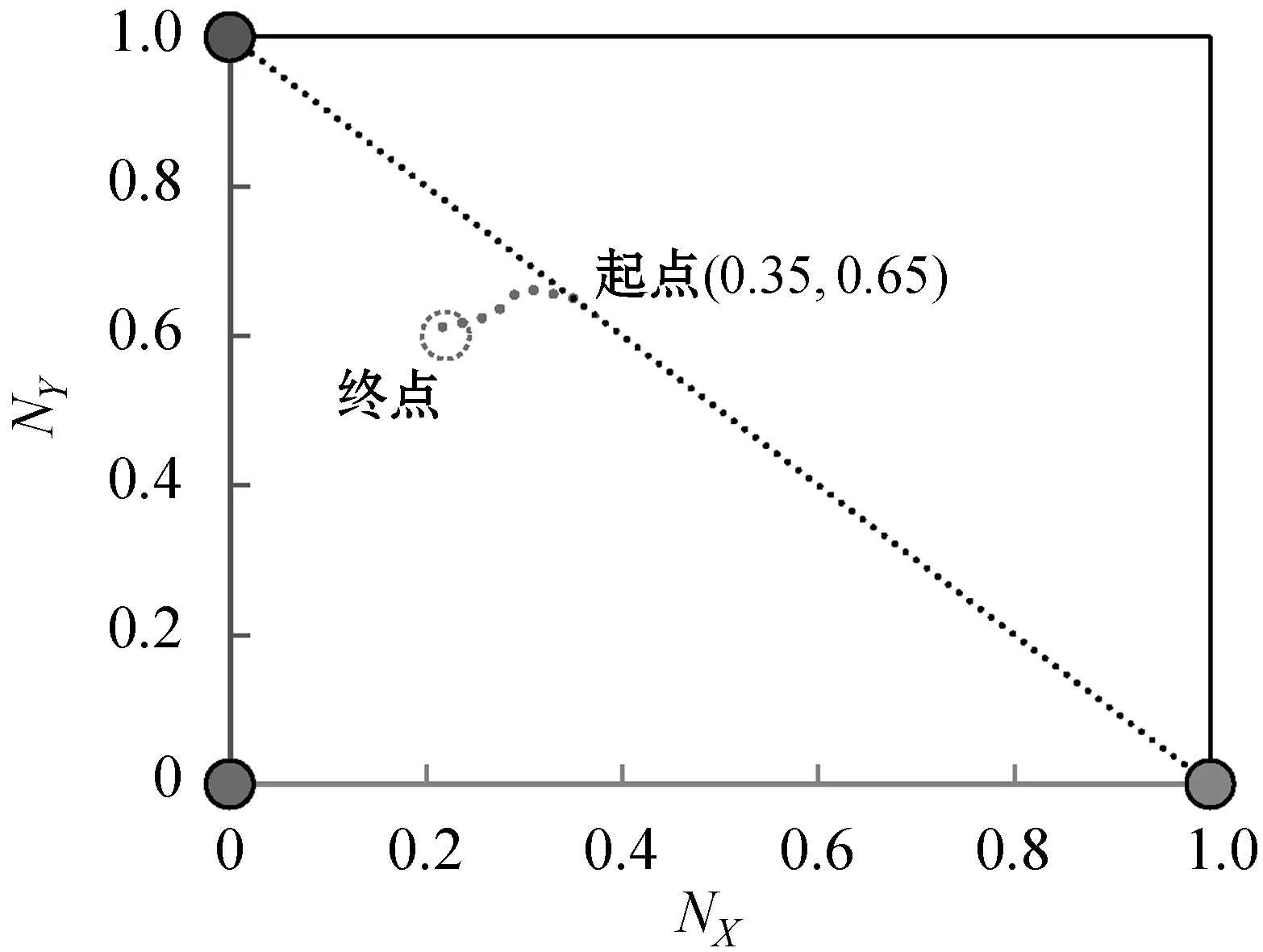
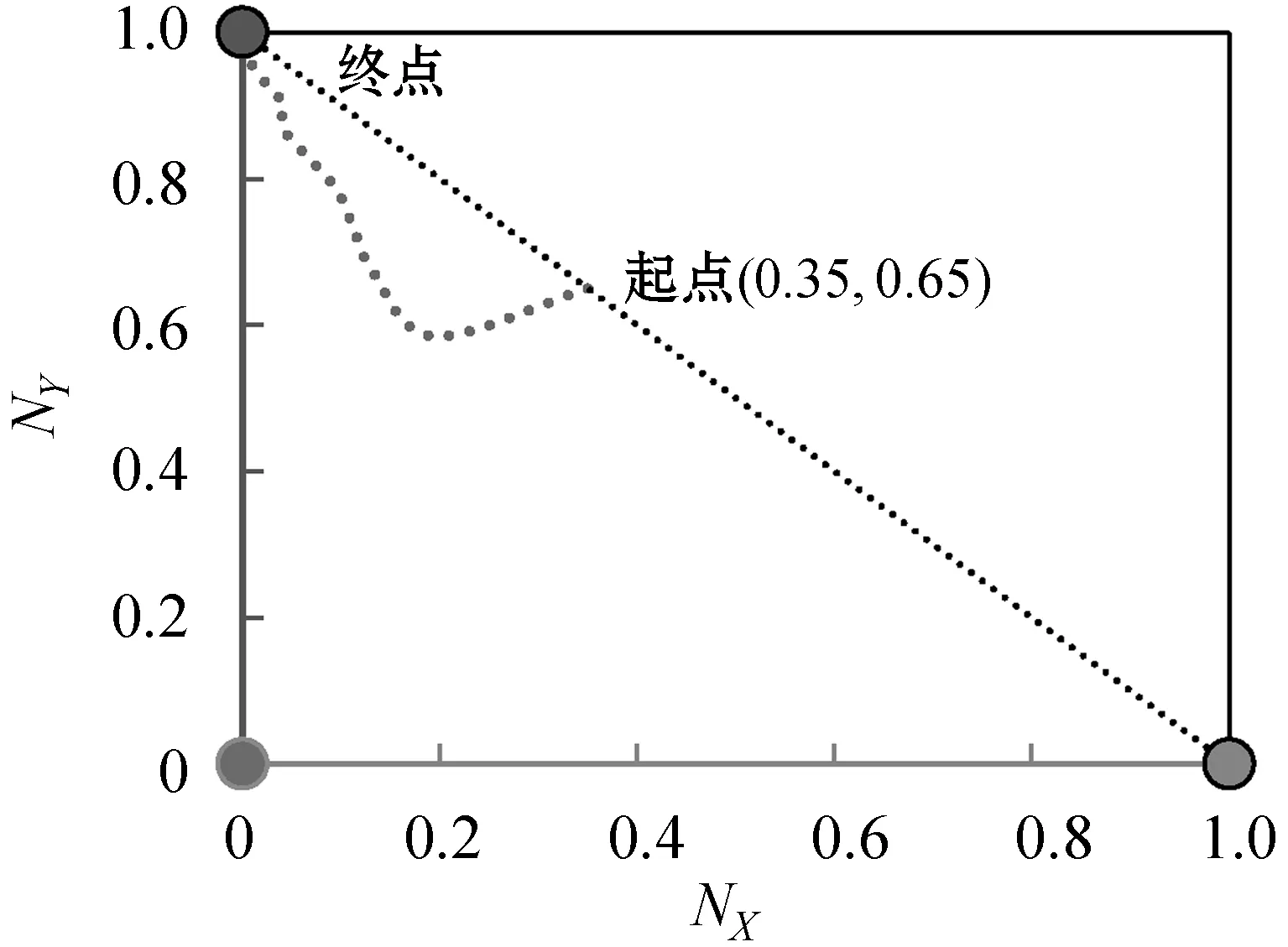
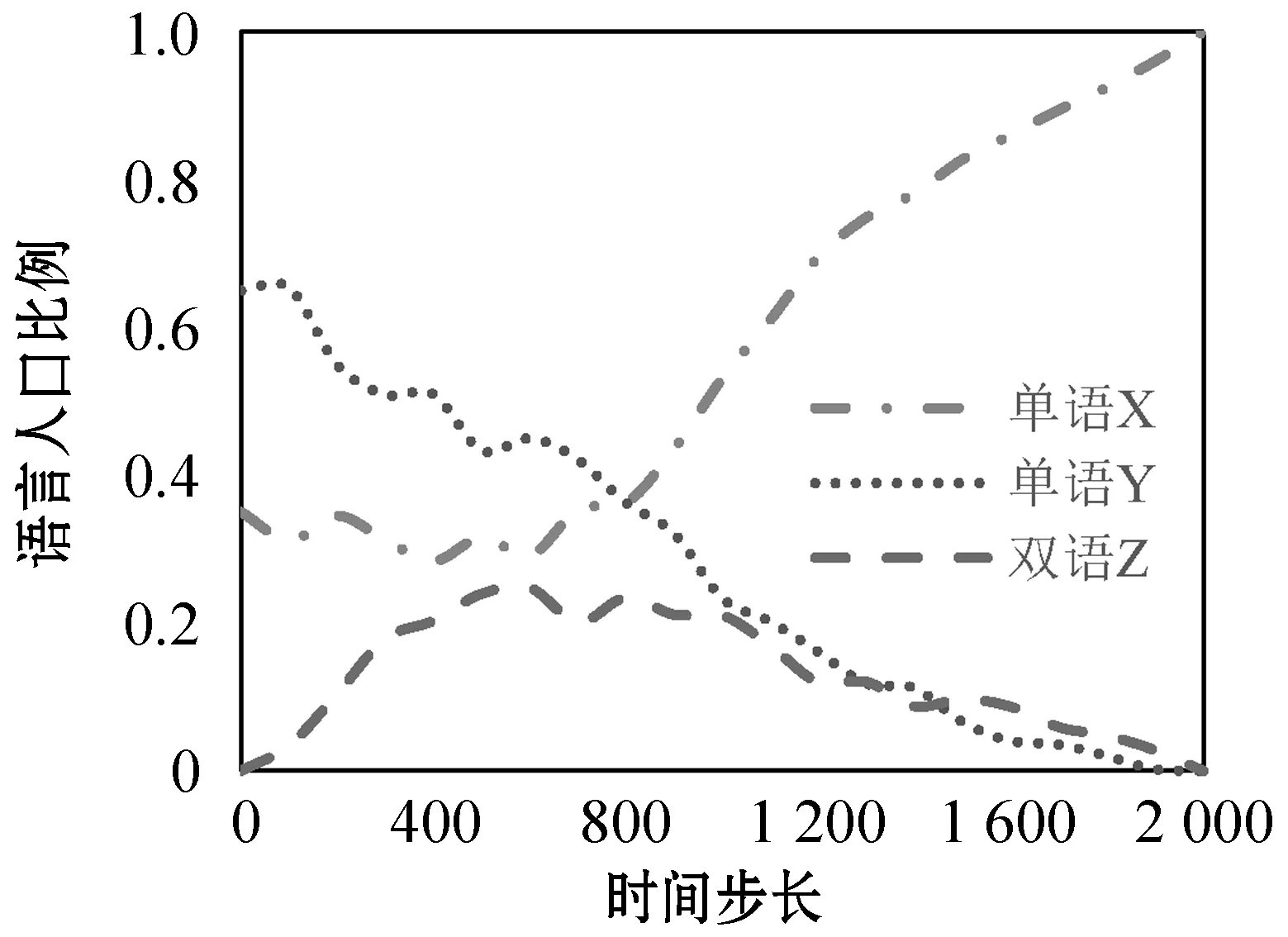
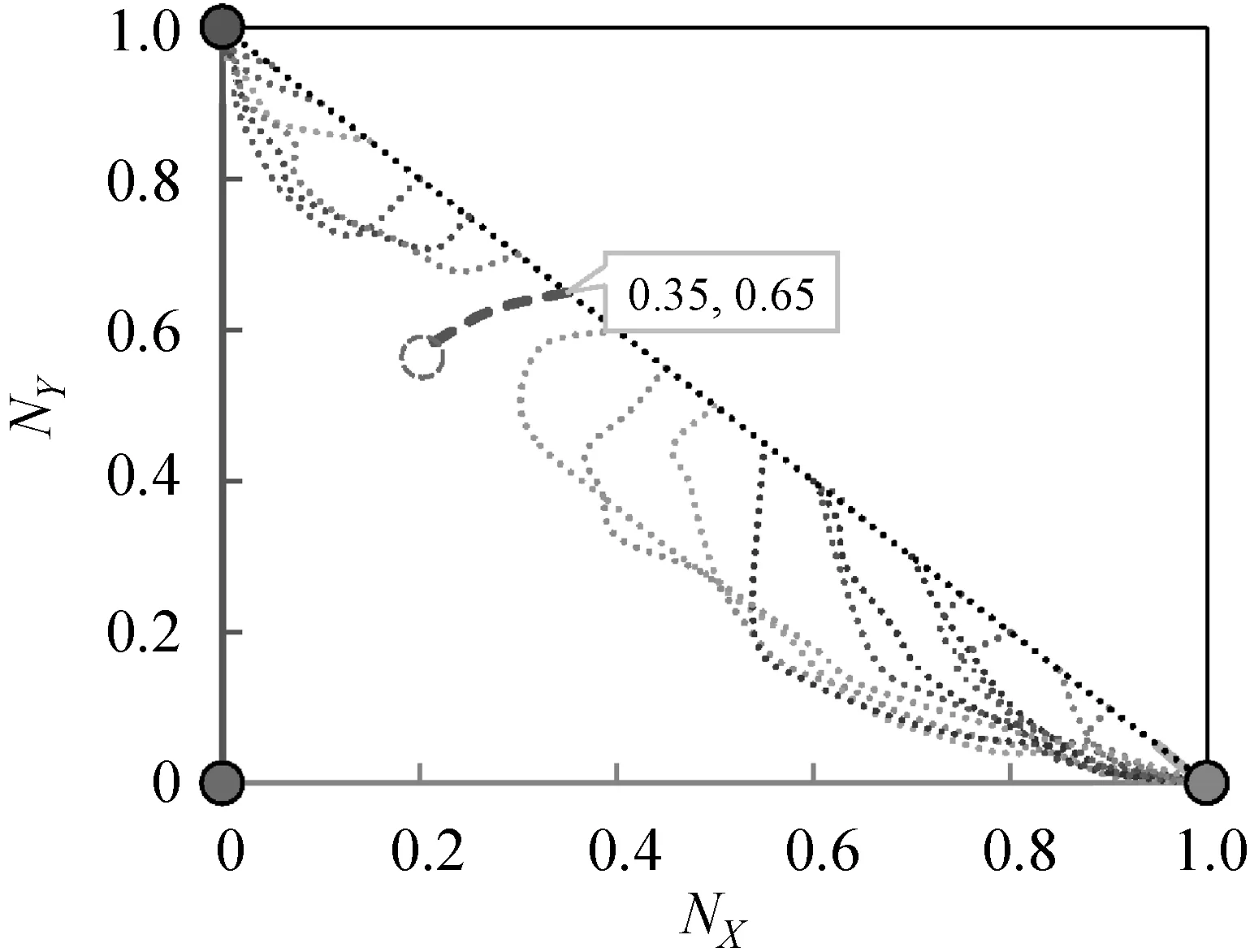
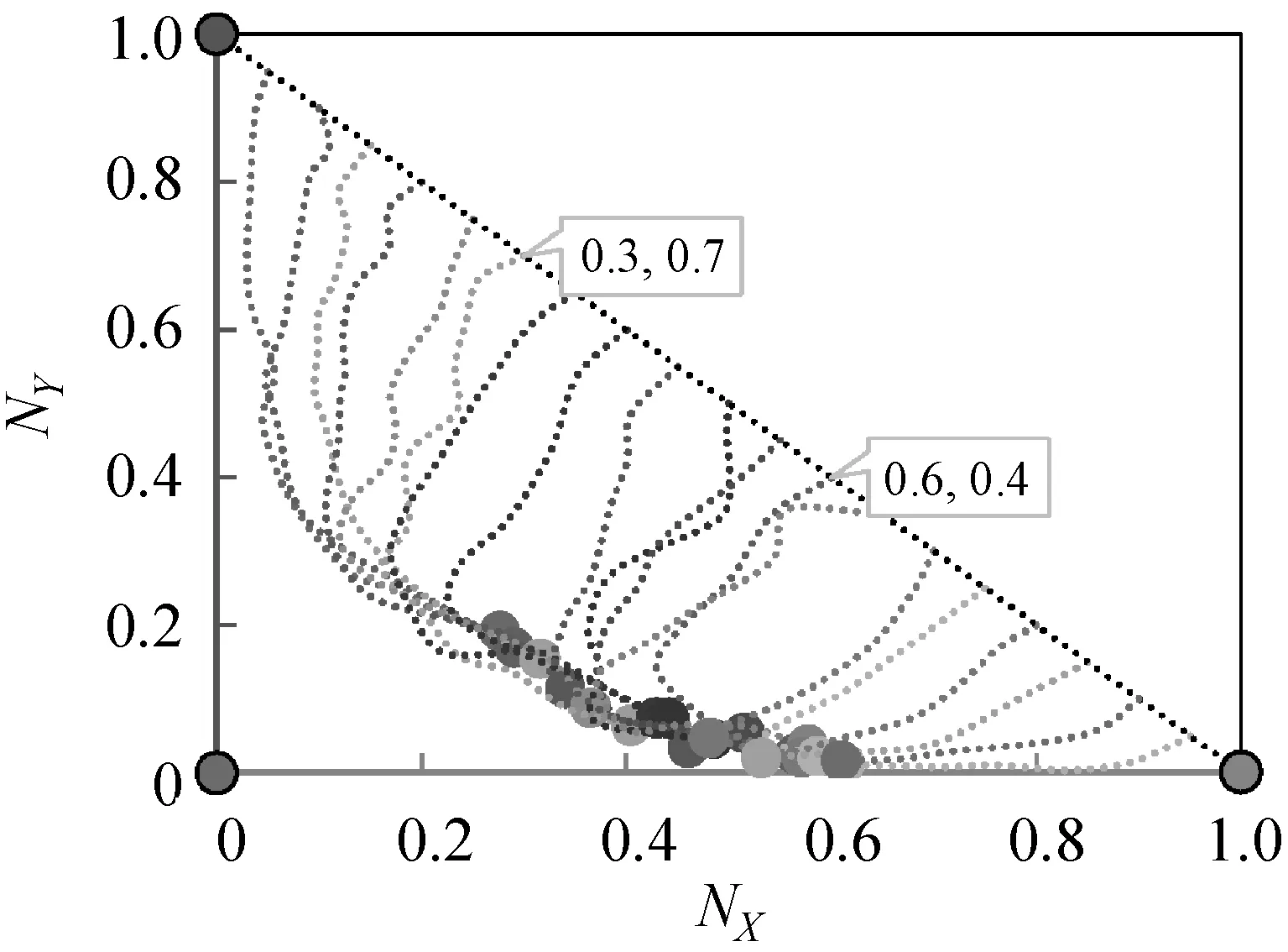
Hamill等[14]提出一種基于agent社會圈子網絡理論來構建動態社會網絡的方法。網絡中的agent賦予不同的社會半徑,以個體agent在二維平面的位置為圓心,以其社會半徑長度構成的圓作為其社會圈子。當兩個agent中心坐標點的連線的長度Q小于等于連線兩端agent較小的社會半徑r時,表示兩個個體agent都處于對方社會圈子內,互相認識,agent間將建立連接關系,否則不建立連接關系。如圖1(a)中Q>r,個體不會建立連接關系,圖1(b)中Q (a) agenti和agentj不產生聯系 (b) agenti和agentj產生聯系 (c) 多社會半徑聯系圖1 社會圈子網絡生成原理 2.1.2遠程社會網絡 圖2 遠程連接 2.1.3具有弱連接關系的社會網絡參數度量驗證 依據上述改進的社會圈子網絡生成模型如圖3(a)所示,圓形節點表示單語者X,正方形節點表示單語者Y,三角形節點代表雙語者Z,星形節點代表無語者W,“—”代表連線兩端的個體建立連接關系。擁有三種不同社會半徑的agent度分布整體都呈現出泊松分布特性,如圖3(b)所示。現實社會中,由于人的交際范圍不同,所以個體的社會圈子大小也因人而異,只有極少數人的社會圈子會很大。有遠程連接的社會圈子網絡度分布比沒有遠程連接的社會圈子網絡度分布高度更低,整體往右,說明有遠程連接的節點平均度更大,即與其相連的鄰居節點數更多,個體的平均網絡規模增大,度相對較低的個體的數量減少。聚類系數分布如圖3(c)所示,整體網絡個體聚類系數平均值在0.57左右,具有較高的聚類系數,加入遠程連接后的聚類系數分布曲線整體往左偏移,平均值聚類系數值為0.42。聚類系數是一個人的任意兩個朋友之間互為朋友可能性的定量描述,是社會網絡關系強弱的一個重要屬性。加入遠程連接的網絡比沒有加入遠程連接的網絡平均聚類系數要低,相當于弱化了朋友關系的強連接,強化了弱連接。計算出網絡沒有加入遠程連接和加入遠程連接后的Pearson系數分別為0.4和0.263,具有度度正相關特點,度度相關雖然仍為正相關,但相關度減小,表示弱連接增強。無遠程連接網絡的平均路徑為6.08,符合社會網絡平均路徑短,即六度分離原則,反映了實際人際關系社會網絡的“小世界”特性[16],加入遠程連接的網絡平均路徑為3.19,大大縮短了路徑。無遠程連接網絡的網絡密度為1.18%,具有密度低的特點,加入遠程連接,網絡密度提高1.78%,但總體而言還是很低,滿足社會網絡低密度特征。 (a) 社會圈子網絡 (b) 度分布 (c) 聚類系數圖3 社會圈子網絡及度量參數 2.1.4雙語教學星型網絡 雙語教育對于保護瀕危語言具有重要影響,為了體現此影響,在建立好的網絡中增加教師節點,設置其數量和教學半徑,使其在二維空間網格中均勻分布。教師節點的數量可以根據需要增加或者減少,通過改變教師節點的數量可以增大或減小雙語教學的力度。如圖4所示,教學半徑內所覆蓋的所有節點都和教師有教學邊相連接,表示教師所負責的教學區域,教師節點數和教師半徑配合,可以確定雙語教學的覆蓋面。 圖4 雙語教學星型網絡 2.2.1agent語言內部結構與語言類型 借鑒文獻[17]中agent的詞匯用二進制位串進行表達的方式,社會語言網絡中agent存在四種語言類型:(1) 單語者X(只掌握X一種語言):agenti(X);(2) 單語者Y(只掌握Y一種語言):agenti(Y);(3) 雙語者Z(掌握X、Y兩種語言):agenti(Z);(4) 無語者W(未掌握任何一種語言):agenti(W)。語言者擁有兩個長度為F的二進制位串LX(v)與LY(v),v∈[1,F],本文中的F設定為20。圖5中,對于agent而言,位串中的1代表相應位置的詞匯是已知的,0代表相應位置的詞匯是未知的。 (a) 單語者X (b) 單語者Y (c) 雙語者Z (d) 無語者W圖5 agent的語言內部結構 語言類型規定:(1)LX(v)中1的個數大于3并且LY(v)中1的個數小于3,規定為單語者X;(2)LX(v)中1的個數小于3并且LY(v)中1的個數大于3,規定為單語者Y;(3)LX(v)和LY(v)中1的個數都大于3時,規定為雙語者Z;(4)LX(v)和LY(v)中1的個數都小于3時,規定為無語者W,對應式(1)-式(4)。 (1) (2) (3) (4) 2.2.2考慮語言態度的語言水平傳播規則 模型中,agent間進行詞匯學習或遺忘需要滿足:(1) agent間具有圖3(a)中的邊連接關系;(2) 在(1)的前提下滿足交流率(Exchange),語言交流率是在社會網絡中有連接關系的兩個agent間進行語言交流的概率,表征agent間語言交流機會的大小。網絡中有邊連接的兩個agent節點滿足交流率時,agent個體間進行詞匯學習或遺忘。根據前人研究[3,5-6],語言學習與語言地位成正比,遺忘與語言地位成反比,在此基礎上本文引入了語言態度的影響。社會語言學表明:語言態度越積極,態度轉變為行為的可能性越高,人們傾向于以更積極的態度學習某種語言,對該種語言學習效率高,遺忘的可能性減小。所以本文近似認為語言學習獲得某一詞匯的概率與語言態度成正比,而遺忘的概率與語言態度成反比,在此基礎上給出新的水平傳播模型,如式(5)-式(12)所示。 X民族對X語言詞匯的學習及遺忘公式: PX(LX)=P×PXX×SX (5) QX(LX)=q×(1-PXX)×SY (6) X民族對Y語言詞匯的學習及遺忘公式: PX(LY)=p×PXY×SY (7) QX(LY)=q×(1-PXY)×SX (8) Y民族對X語言詞匯的學習及遺忘公式: PY(LX)=p×PYX×SX (9) QY(LX)=q×(1-PYX)×SY (10) Y民族對Y語言詞匯的學習及遺忘公式: PY(LY)=p×PYY×SY (11) QY(LY)=q×(1-PYY)×SX (12) 式中:p代表學習率(p∈[0,1]);q代表遺忘率(q∈[0,1]);SX(SX∈[0,1])和SY(SY∈[0,1])分別表示X語言和Y語言的語言地位,并且SX+SY=1;PXX代表X民族對學習X語言詞匯的態度;PXY代表X民族對學習Y語言詞匯的態度;PYX代表Y民族對學習X語言詞匯的態度;PYY代表Y民族對學習Y語言詞匯的態度。 圖6(a)為X民族對X語言詞匯的學習及遺忘過程,agenti為X民族,agentj為X民族或Y民族,個體agenti與其具有連接關系的agentj對應位置的X詞匯掌握情況不同(位串中的二進制數不同):(1) 學習:agenti中未知該詞匯(位串中的數字為0)而agentj已知(位串中的數字為1),則agenti中對應位串中的數字將以PX(LX)的概率由0變為1(式(5));(2) 遺忘:agenti中已知該詞匯(位串中的數字為1)而agentj未知(位串中的數字為0),則agenti中對應位串中的數字將以QX(LX)的概率由1變為0(式(6))。圖6(b)為X民族對Y語言詞匯的學習及遺忘過程,agenti為X民族,agentj為X民族或Y民族,個體agenti與其具有連接關系的agentj對應位置的Y詞匯掌握情況不同(位串中的二進制數不同):(1) 學習:agenti中未知該詞匯而agentj已知,則agenti中對應位串中的數字將以PX(LY)的概率由0變為1(式(7));(2)遺忘:agenti中已知該詞匯而agentj未知,則agenti中對應位串中的數字將以QX(LY)的概率由1變為0(式(8))。agenti為Y民族的詞匯學習和遺忘原理如同X民族,考慮語言態度的詞匯學習和遺忘公式見式(9)-式(12)。 (a) X民族對X詞匯的學習和遺忘過程示意圖 (b) X民族對Y詞匯的學習和遺忘過程示意圖圖6 X民族對X、Y語言詞匯學習與遺忘過程 2.2.3語言垂直傳播規則 社會人口數量的動態變化可以通過人口的出生和死亡來體現,此過程需要考慮父輩語言的遺傳以及子輩對語言的繼承,語言的垂直傳播規則可以反映這一過程。模型通過設置出生率以及死亡率來體現社會人口數量的動態變化。 CAS[5]、MWAS[6]和ZAS[7]模型中子代傳承父輩的語言規則為:父輩為單語者x(或y),則子代也只能傳承單語x(或y);當父輩為雙語者Z時,子代傳承x(或y)單語的概率受到x(或y)的語言地位以及網絡鄰域中單語者x(或y)比例的影響。我們基于新的語言競爭機制,給出改進的垂直傳播規則:(1) 個體對雙語的態度越積極,雙語遺傳給子代的概率越大;個體對雙語的態度越不積極,雙語父輩遺傳單語給子代的概率越大。(2) 個人社會網絡鄰域雙語人群越多,子代繼承雙語的可能性越大;個人社會網絡鄰域某種單語人群比例越高,子代繼承該種單語的可能性越大。(3) 父輩雙語者的語言中,某種語言地位越高,該種單語言遺傳給子代的概率越大,反之越小。 基于以上規則給出改進的垂直傳播公式,如式(13)-式(17)所示。(1)當父輩為單語者時,子代只能直接繼承父輩的單語,如式(13)和式(14)所示。(2) 父輩為雙語者,在滿足概率P(Z→Z)條件下,子代繼承父輩的雙語特性,如式(17)所示。(3) 父輩為雙語者,在不滿足P(Z→Z)概率條件下,如果滿足概率P(Z→X)時,子代僅繼承單語X;如果滿足概率P(Z→Y)時,子代僅繼承單語Y,如式(15)和式(16)所示,公式表明,雙語遺傳單語與該種語言的語言地位、人口密度和對雙語的不積極態度成正比。 P(X→X)=1 (13) P(Y→Y)=1 (14) (15) (16) P(Z→Z)=1-P(Z→X)-P(Z→Y) (17) 式中:nX代表agent社會半徑圈子內講X語言的人的個數;nY代表agent社會半徑圈子內講Y語言的人的個數;nZ代表agent社會半徑圈子內講雙語的人的個數;nS代表agent社會半徑圈子內所有人的個數;Pa代表人們對學習雙語的態度,子代繼承父代雙語的概率與Pa成正比,在這里Pa=min{PXX、PXY、PYX、PYY};(1-Pa)表示對雙語的不積極態度。 2.2.4agent雙語教學規則 語言教學發生在教師節點agent與語言學習者agent有邊連接的兩個節點之間,教學規則滿足如下: (1) 設置教學的時間間隔(teachtime=3),即一次教學與下次教學之間間隔的時間步長,教學不是每個時間步都會發生,只有處在教學步時才會進行雙語教學,反映教學分頻次。 (2) 設置的教學邊是一種單向的教學(即教師只教不學),在這里有兩種教學方式,一種是僅對教學半徑內弱勢語言所在的民族(Y)進行雙語教學;另一種是對教學半徑內的所有人進行雙語教學,不管其民族。 (3) 設置教學率(teachrate=5%),由于人們在學習過程中會出現遺忘現象,在此設置教學率來表征每次教學成功的概率。一旦滿足該概率,教師節點會將自己詞匯表中的詞匯隨機選擇一位自己已知人們未知的詞匯進行教學,人們相應未知的詞匯就會變為已知。圖7為X語言詞匯的教學過程,Y語言詞匯的教學過程與X語言相同。 圖7 X語言詞匯的教學過程 (1) 生成peoples節點并設置其屬性:創建一個250×241范圍內的二維空間網絡,在網絡中隨機生成nofArea個agents,在創建的agent中分配X單語者和Y單語者的人口比例(nofx、nofy),且nofx+nofy=1;設置單語者X的民族為X,設置單語者Y的民族為Y,設置兩種語言的語言地位,SX代表X的語言地位,SY代表Y的語言地位,且SX+SY=1;設置agents身份為people,為peoples分配社會半徑并設置三種社會半徑的人口分布比例(Spop、Mpop和Bpop)且Spop+Mpop+Bpop=1。 (2) 建立教師節點并設置其屬性:創建nofteachers個agents均勻分布在二維空間網絡中,設置其語言類型為雙語Z,并設置其身份為teacher;設置教學半徑(teachingcircle)、教學率(teachrate)、教學間隔(teachtime)的大小。 (3) agents詞匯設置:agents擁有兩個長度為20的二進制位串LX(v)與LY(v),v∈[1,20],1表示已知詞匯,0表示未知詞匯。為peoples節點每種語言分配高中低三種詞匯占比,設置單語者X的LX(v)中1的個數大約為17個的占比為h,1的個數大約為14個的占比為m,1的個數大約為10個的占比為l,LY(v)中全為0。設置單語者Y的LY(v)中1的個數大約為17個的占比為h,1的個數大約為14個的占比為m,1的個數大約為10個的占比為l,LX(v)中全為0,且h+m+l=1。設置teachers節點二進制位串LX(v) 與LY(v)中1的個數大約為19個。教師節點的語言類型和所掌握的詞匯一旦初始設置,在程序運行過程中不會發生改變。 (4) 生成社會網絡:peoples類型agent根據自身的社會半徑建立社會網絡,如圖3(a);teachers根據自身圈子大小建立星型網絡,如圖4所示。 (5) 個體語言交流:個體的語言交流首先滿足在彼此的社會半徑范圍內,其次要滿足交流率(Exchange)。當達到上述條件下,進行語言的內部詞匯交流,具體如式(5)-式(12)。 (6) 人口流動與網絡更新:設置日常移動和長距離移居比例,peoples根據此比例進行移動,移動后個體agent根據其社會半徑和社會圈子連接規則重新生成社會網絡。設置遠程連接的比例、遠程連接的社會半徑和遠程連接的時間,構建遠程社會網絡。 (7) 判斷死亡/出生人口并分配后代語言:遍歷網絡中的所有agent,當滿足出生概率時個體繁殖后代,當滿足死亡概率時個體死亡。當父輩為單語時(X或Y),子代也為同類型單語者,并繼承父輩的全部詞匯。當父輩為雙語個體Z時,并滿足雙語遺傳概率P(Z→Z)時,子代也為雙語者類型,并繼承父輩的全部詞匯;當父輩為雙語個體Z時,在不滿足雙語遺傳概率的前提下,如果滿足概率P(Z→X)時僅繼承單語X,即LX(v)中的詞匯全部繼承,LY(v)中的詞匯全為0;如果滿足概率P(Z→Y)時僅繼承單語Y,即LY(v)中的詞匯全部繼承,LX(v)中的詞匯全為0。 (8) 重構社會語言網絡:經過移動、人口出生、死亡后,利用社會圈子生成原理及其改進方法重新更新語言交流網絡,利用星型網絡原理重新生成雙語教學網絡。 (9) 雙語/單語者的判定:根據式(1)-式(4),判斷和統計agent的語言類型。 (10) 網絡的動態更新:隨著時間的增加,反復執行步驟(5)-步驟(10),直到達到預設的時間網絡停止更新。 本模型研究在混居的條件下,通過構建具有遠程連接關系社會網絡和雙語教學網絡雙層混合網絡,研究語言態度和雙語教學作為調控政策條件下系統的語言競爭演化規律。該網絡模型以NetLog[18]為平臺,主要參數的初值借鑒了文獻[5,14,19]中的設定,如表1所示。 表1 模型主要參數的初值 續表1 在文獻[3,5]中,系統演化的結果有穩定和不穩定兩種均衡點,不穩定點會隨機按一定的概率滑向穩定點。弱勢語言最終會消亡,系統不能達到共存狀態,模型用微分方程構建,其動力學特性由系統的方向圖來描述。在文獻[6]中,通過干預機制調控語言地位可以使系統的不穩點變為穩定點,強勢語言和弱勢語言在系統可以達到共存狀態。構建的語言競爭微觀模型首次利用軌跡圖分析系統解的空間狀態,認為軌跡圖與方向圖高度近似,可以用軌跡圖代替方向圖分析系統的演化特征。語言競爭演化系統中以強勢語言單語者比例NX、弱勢語言單語者比例NY、雙語者的比例NZ為系統演化的考察變量,來分析系統長期演化的動力學特性,由于系統中NZ=1-NX-NY,在此用系統的軌跡圖來描述系統的動力學機制,系統的軌跡圖是指系統中X、Y語言人口比例(NX、NY)隨時間增長演化的軌跡,如圖8所示,軌跡圖是在二維坐標中從起點到終點每個點對應系統時序演化的一個時刻。系統主要的仿真參數設置如表1所示,經過大量實驗表明,在表1初始條件下,系統大部分情形通過t=800步左右而達到穩定狀態,最長的演化情形在t=1 200步左右進入穩定狀態,即系統演化狀態不再發生改變。所以我們認為t=2 000可以近似看成系統在t=∞時的演化狀態。在系統演化過程中,存在不穩定均衡點,即在相同初始條件下,有不同的最終演化結果,如圖8所示。圖8(a)顯示了隨時間增長三種語言人口比例的演化趨勢,圖8(b)是對應于圖8(a)的軌跡圖,在這次運行中,系統迅速收斂到均衡點(x,y,z),即三種語言共存;圖8(c)顯示了與圖8(a)相同的初始條件下系統的演變,通過軌跡圖8(d)可以看到系統最終收斂到均衡點(0,1,0),即系統中只有單語者Y;圖8(e)與圖8(a)的初始條件相同,系統通過軌跡圖8(f)可以看到收斂到均衡點(1,0,0),即系統中只有單語者X。 (a) 不穩定均衡點情形一 (b) 對應于圖8(a)的系統軌跡 (c) 不穩定均衡點情形二 (d) 對應于圖8(c)的系統軌跡 (e) 不穩定均衡點情形三 (f) 對應于圖8(e)的系統軌跡圖8 系統在不穩定均衡點處的演化趨勢 經過大量的實際調研表明,我國的少數民族語言大部分存在衰退情況,部分存在瀕危現象。根據其所處地理社會環境不同,可以分為母語保持型(聚居)、母語衰退型(雜居)和母語瀕危型(高度雜居)三類。某一地區的語言使用狀況是各種因素相互作用的結果,主要影響因素除了語言地位外有居住地理環境、語言態度、社區語言環境、家庭語言環境、學校采用單語或雙語教學等。這些因素相互影響,導致不同區域的語言態勢不同。如表2所示的云南里山鄉彝族語言使用狀況顯示同時存在三種母語保持類型[11],具有廣泛的代表性。可以看出,母語保持較好的類型存在于交通偏遠、地理隔離、人口流動少的區域;而雜居和漢語包圍型雜居區域母語態勢主要以衰退和瀕危態勢為主。而隨著社會進步、交通發達,人們的社會流動和社會網絡正在發生快速變化,地球村越來越明顯,靠地理隔離實現少數民族語言保持的區域正在快速消失,更多的區域向語言衰退和瀕危態勢轉變,語言保護形勢快速惡化,尋找更有力的語言保護方案時不我待。下面將對這三種類型及其政策改進情形下的語言演化趨勢進行仿真計算實驗。 表2 云南里山鄉彝族語言的使用現狀 3.2.1仿真情形一 由于社會經濟發展不均衡,仍有部分地區交通閉塞,處于相對封閉的環境,人口分布密度較高,遠離漢文化中心,漢語文化教育處于相對落后的狀態,少數民族語言在生活領域中發揮著巨大的作用。例如表2中的第一種類型,在該情形下,漢語為強勢語言,少數民族語言(彝語)為弱勢語言;不同民族的語言態度為:彝族對母語認可度高,對漢語認可度一般,漢族對漢語的認可度高,對彝語的認可度一般;社區學校僅進行漢語單語教學。參照以上情形,主要的仿真參數設置如下:強勢語言的社會地位SX=0.6,弱勢語言的社會地位SY=0.4,強勢語言民族對母語的態度PXX=0.7,對弱勢語言的態度PXY=0.3,弱勢語言民族對強勢語言的態度PYX=0.3,對母語的態度PYY=0.7。以下將以該情形為基準分析系統解的狀態空間,以及改善語言態度和加入教師節點進行雙語教學調控后系統解狀態空間的變化。圖9(a)系統的最終狀態取決于單語者X、Y的初始比例。當單語者Y的初始占比大于等于0.7時,系統最終收斂到(0,1,0),系統中只剩弱勢語言Y,弱勢語言完全保持;當單語者Y的初始占比范圍在0.6~0.7時,系統收斂到(x,y,z),是一種三語共存狀態,但是實際中很難保持這樣的條件實現均衡穩定,是不穩定點;當單語者Y的初始比例低于0.7時,系統最終收斂到(1,0,0),只剩強勢語言X。圖9(b)為在此基礎上加入教師節點僅對弱勢語言所在的民族(Y)進行雙語教學,當單語者Y的初始人口占比大于等于0.7時,系統最終收斂到(x,y,z),NX范圍在0.22~0.55之間,NY范圍在0.05~0.25之間,是一種三語共存狀態,即以強勢語言和雙語占比為主,少量弱勢語言的共存態;當單語者Y的初始人口占比小于0.7時,系統最終收斂到NX軸上,NX范圍在0.68~1.00之間,即強勢語言X和雙語Z共存,共存狀態可以在大部分條件下實現。圖9(c)為在基準情形下加入教師節點對區域內所有人進行雙語教學,系統最終收斂到(x,y,z),NX范圍在0.3~0.6之間,NY范圍在0~0.2之間,以強勢語言和雙語占比為主,少量弱勢語言的一種共存態,弱勢語言可以很好地以雙語的形式保存下來。橫向對比,在圖9(a)中,雙語的存在是一種不穩定均衡點。在圖9(b)中,雙語幾乎全部是由弱勢語言轉化而來,雙語比例范圍在0~0.55之間,波動范圍廣。在圖9(c)中,雙語比例較圖9(b)增多,雙語比例范圍在0.40~0.54之間,波動范圍相對集中;雙語不僅僅是由弱勢語言轉化而來,強勢語言也有一部分會轉化成雙語。 (a) 基準情形 (b) 僅對弱勢語言所在的民族進行雙語教學 (c) 對區域內所有人進行雙語教學圖9 情形一下的系統軌跡 隨著社會發展,交通便利,開始重視漢文化教育,對漢語的認識普遍提高,弱勢民族對強勢語言的態度也在逐漸改善。在上述主要的仿真參數不變的情況下,僅將弱勢語言民族對強勢語言的態度PYX從0.3提高到0.7,以下以該情形為基準分析系統解的空間狀態,以及改善語言態度和加入教師節點進行雙語教學調控后系統解空間狀態的變化。從圖10(a)中可以看出無論單語者X和單語者Y的初始人口占比是多少,經過2 000步,系統最終都收斂到(1,0,0),只剩強勢語言X,并且隨著單語者X的初始占比越大,到達最后的平衡態所需要的時間就會越短。與圖9(a)相比,系統在演化過程中出現更多的雙語者Z,弱勢語言Y不能保持。圖10(b)為在此基礎上加入教師節點僅對弱勢語言所在的民族(Y)進行雙語教學,系統最終幾乎都收斂到NX軸上,NX范圍在0.39~1.00之間,即強勢語言X和雙語Z共存。與圖9(b)相比,無論單語者X和單語者Y的初始人口占比多少,弱勢語言Y最終都會消亡;隨著單語者X的占比越大,系統最終共存態中雙語者Z的占比就會越小,弱勢語言很難保留下來。圖10(c)為在基準情形下加入教師節點對區域內所有人進行雙語教學,系統最終收斂到(x,y,z),NX范圍在0.32~0.54之間,NY范圍在0~0.05之間,以強勢語言和雙語為主,少量弱勢語言的一種共存態。與圖9(c)相比,弱勢語言民族對強勢語言的認可度提高,系統最終狀態的動態變化范圍變小。 (a) 提高PYX (b) 僅對弱勢語言所在的民族進行雙語教學 (c) 對區域內所有人進行雙語教學圖10 情形一下改變態度之后系統的軌跡 3.2.2仿真情形二 當今社會經濟發展迅速、交通發達、人口流動大、漢文化滲透較快,大部分少數民族地區以漢語為主,本民族語言趨向消亡,該種現象越來越普遍。例如表2中的第二種類型和第三種類型,在該情形下,漢語為強勢語言,少數民族語言(如:彝語)為弱勢語言,不同民族的語言態度為:彝語對母語認可度低,對漢語認可度高,漢語對漢語的認可度高,對彝語的認可度低,社區學校僅進行漢語單語教學。主要的仿真參數設置如下:強勢語言民族對母語的態度PXX=0.7,對弱勢語言的態度PXY=0.3,弱勢語言民族對強勢語言的態度PYX=0.7,對母語的態度PYY=0.3。以下將以該情形為基準分析系統解的空間狀態,以及改善語言態度和加入教師節點進行雙語教學調控后系統解空間狀態的變化。從圖11(a)中可以看出無論單語者X和單語者Y的初始人口占比是多少,經過2 000步,系統最終都收斂到(1,0,0),只剩強勢語言X,并且隨著單語者X的初始占比越大,到達最后的平衡態所需要的時間就會越短;圖11(b)為在此基礎上加入教師節點僅對弱勢語言民族(Y)進行雙語教學,系統最終都收斂到NX軸上,NX范圍在0.6~1.0之間,即強勢語言X和雙語Z的一種共存態,共存態中單語者X的占比遠高于雙語者Z的占比,并且隨著單語者X的占比越大,系統最終共存態中雙語者Z的占比就會越小;圖11(c)為在基準情形下加入教師節點對區域內所有人進行雙語教學,系統最終收斂到NX軸上,NX范圍在0.54~0.72之間,即強勢語言X和雙語Z的一種共存態,共存態中強勢語言的占比更高。橫向對比,在圖11(a)中,在演化的過程中會出現雙語,但系統最終的狀態是強勢語言勝出,雙語不能長時間存在。在圖11(b)中,雙語大部分是由弱勢語言轉化而來,少部分是由強勢語言轉化而來,雙語比例范圍在0~0.4之間,波動范圍相對較廣。在圖11(c)中,雙語比例較圖11(b)增多,雙語比例范圍在0.40~0.54之間,波動范圍相對集中,雙語是由弱勢語言和強勢語言共同轉化而來。 (a) 基準情形 (b) 僅對弱勢語言所在的民族進行雙語教學 (c) 對區域內所有人進行雙語教學圖11 情形二下的系統軌跡 現實生活中仍存在一些特例,強勢語言和弱勢語言之間相互兼用,形成一個語言和諧的社會,這種兼用不是來自法律法規的要求,而是來自生活的需要,屬于“自然兼用型”,這樣的語言社會,雙方對兩種語言的態度都很積極。在上述主要的仿真參數不變的情況下,僅將強勢語言民族對弱勢語言的態度PXY從0.3提高到0.7,弱勢語言民族對強勢語言的態度PYX從0.3提高到0.7,其他仿真參數不變。以下將以該情形為基準分析系統解的空間狀態,以及改善語言態度和加入教師節點進行雙語教學調控后系統解空間狀態的變化。從圖12(a)中可以看出,當單語者Y的比例大于等于0.8時,系統收斂到(x,y,z),即強勢語言和雙語的一種共存態;NX范圍在0.08~0.27之間,NY范圍在0.06~0.16之間,是一種三語共存狀態,即以雙語占比為主,少量單語的共存態;當單語者Y的比例小于0.8時,系統最終收斂到NX軸上,NX范圍在0.29~1.00之間。與圖11(a)相比,系統不再是強勢語言X勝出,在單語者Y占比高的情況下,弱勢語言Y可以轉化為雙語很好地保存下來。隨著單語者X的占比越大,系統最終共存態中雙語者Z的占比就會越小。圖12(b)為在此基礎上加入教師節點僅對弱勢語言民族(Y)進行雙語教學,系統最終收斂到NX軸上,NX范圍在0~1之間,即強勢語言X和雙語Z的一種共存態,動態變化范圍很大。與圖11(b)相比,共存態中不再是單語者X的占比更高,在大多數情況下,共存態中雙語者Z的占比更高。圖12(c)為在基準情形下加入教師節點對區域內所有人進行雙語教學,無論單語者X和單語者Y的初始人口占比是多少,系統最終收斂到NX軸上,NX范圍在0.07~0.17之間,NX值很小,NY幾乎為0。與圖11(c)相比,系統最終講單語的人很少,幾乎達到了一個全民雙語的狀態,弱勢語言Y可以很好地保存下來。 (a) 同時提高PXY和PYX (b) 僅對弱勢語言所在的民族進行雙語教學 (c) 對區域內所有人進行雙語教學圖12 語言和諧下系統的軌跡 前面研究了系統不同初始條件下動力學特性,即系統的演化趨勢,本節研究動態調控措施對正在演化的系統動力學特性的影響。動態調控是指系統在某個初始條件下的演化過程中,在某個時刻開始對系統進行政策調控干預,即從該時刻改變系統某些參數的值看政策調控干預對系統演化趨勢的影響。在這里我們對設定初始條件下的系統演化過程的弱勢語言的比例(包括雙語者)進行監控,當該區域的弱勢語言人口比例低于設定的閾值時,啟動政策調控,然后觀察政策調控對系統演化的影響。 通過對上述模型參數的分析,改變民族對語言的態度和加入教師節點進行雙語教學,可以明顯地改變系統的演化態勢,變不穩定均衡點為穩定均衡點,實現弱勢語言保持。為了驗證此模型的有效性,以圖11(a)為基準進行分析,探討在NX=0.5、NY=0.5的初始人口占比的條件下,弱勢語言者和雙語者兩者的比例低于30%時(大約360步的時候)進行調控來看系統未來演化趨勢的變化,尋求合適的調控時機和力度來阻止弱勢語言的消亡。(1) 如圖13所示,僅改變一個態度(PYY從0.3變為0.7)和改變兩個態度(PXY從0.3變為0.7,PYY從0.3變為0.7),調控后比調控前在弱勢語言滅亡的時間上進行了延長,圖14(a)為無調控的平均詞匯量,圖14(b)為僅改變一個態度的平均詞匯量,詞匯演化的趨勢幾乎沒有太大的變化,速度會變慢,改變兩個態度的平均詞匯量與圖14(b)非常類似,在此沒給出。實驗表明,當弱勢語言有瀕危跡象的時候再去改變對弱勢語言的態度只能延緩弱勢語言的滅亡,而不能扭轉其滅亡的結局。(2) 在改變態度的基礎上加入教師節點(教學率為5%(Y)),僅對Y民族的群體進行雙語教學,在2 000步時,單語者Y和雙語者Z的總比例達到了32.94%,幾乎都是由Y民族的人轉化而來。圖14(c)中,Y民族的Y詞匯平均個數為4.01個,數量很低,只能適用于一些簡單的交流場合,X民族的Y詞匯平均個數幾乎為0。如果教師節點是對區域內的所有人進行雙語教學(教學率為5%(S)),單語者Y和雙語者Z的總比例達到了58.88%,數量上面有了明顯的提高。圖14(d)中,X民族Y詞匯的平均個數增加到了2.79個,Y民族Y詞匯平均個數為4.69,變化不大。(3)將教學率提高到15%,僅對Y民族的人進行雙語教學(教學率為15%(Y)),單語者Y和雙語者Z的總比例為53.56%。圖14(e)中,Y民族Y詞匯的平均個數為8.48個,X民族Y詞匯的平均個數為1.39個,當教師節點對區域內所有人進行雙語教學(教學率為15%(S)),單語者Y和雙語者Z的總比例為84.37%,幾乎相當于全民雙語,與教學率為5%相比,詞匯的平均個數也有了很大的改善,Y民族Y詞匯的平均個數為9.62個,X民族Y詞匯的平均個數為7.03個。綜上所述,該模型可以讓語言人口比例和平均詞匯量保持在比較理想的狀態,改變語言未來的演化趨勢,使弱勢語言能夠以雙語的形式保存下來。 圖13 不同調控政策下單語者Y和雙語者Z總人口比例的變化 (a) 無調控平均詞匯量 (b) 僅改變一個態度的平均詞匯量 (c) 教學率為5%(Y)的平均詞匯量 (d) 教學率為5%(S)的平均詞匯量 (e) 教學率為15%(Y)的平均詞匯量 (f) 教學率為15%(S)的平均詞匯量圖14 平均詞匯量 本文引入虛擬鏡像概念構建了新的社會網絡,網絡既有社區內強連接關系也有跨社區遠程弱連接關系。增加了教師節點與學習者節點構成的星型教學網絡,教師agent可以對網絡中學習者agent實施雙語教學。以二進制字串代表agent的內部詞匯結構,給出改進的agent語言水平傳播和垂直傳播公式,傳播公式綜合考慮了語言態度、語言地位和網絡連接關系類型,構建了語言水平、垂直傳播網絡和語言教學網絡組成的二層語言競爭動態社會網絡微觀仿真模型。模型研究語言態度和雙語教學作為調控政策條件下系統的語言競爭動力學特性,重點分析當代社會網絡條件下典型弱勢語言生存環境情形下系統的演化趨勢,以及改變語言態度和加入教師節點進行調控后系統演化趨勢的改變。大量的仿真實驗表明:在社會網絡遠程弱連接增強的趨勢背景下,即使是弱勢語言人口占絕對優勢,也很難避免弱勢語言消亡的趨勢;社區保護弱勢語言要提高全民對弱勢語言和雙語的態度,同時在社區構建雙語價值社會,實施全民雙語教育可以引導系統向穩定的全民雙語型演化。而這些政策及其組合已經被社會語言學研究證明是行之有效的,本文的仿真模型解釋和驗證了政策的作用機制和有效性。但模型的許多方面仍需改善,沒能將語言水平考慮在內,每個人的語言態度因語言水平而異,未來的研究將在此基礎上進一步改進模型以便更加切合實際社會。

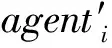



2.2 新型agent微觀模型





2.3 語言競爭agent網絡演化模擬模型
3 模型計算實驗


3.1 軌跡圖與系統演化狀態



3.2 不同條件下仿真實驗











3.3 動態調控仿真實驗







4 結 語

