改進自適應抗差容積卡爾曼濾波多源室內定位

李 鵬，榮冬成，向宇翔，凌智琛，夏 珺

(湘潭大學自動化與電子信息學院，湖南湘潭 411100)

0 引言

在組合導航系統中，高精度的濾波算法對導航定位的解算精度具有重要的影響。擴展卡爾曼濾波(Extended Kalman Filter，EKF)雖然可以用于非線性系統濾波，但是其線性化環節會引入高截斷誤差，且Jacobi矩陣的計算會增加運算的難度，在實際工程應用中效果不佳。無跡卡爾曼濾波(Unscented Kalman Filter，UKF)克服了EKF的局限性，基于無味變換(Unscented Transformation， UT)構建了一系列Sigma點，以逼近狀態向量的后驗概率密度函數，實現簡單且精度遠高于EKF；但是UKF在系統狀態量發生突變的情況下魯棒性較差，其精度容易受到影響。容積卡爾曼濾波(Cubature Kalman Filter，CKF)利用三階球面徑向容積準則，對概率密度函數進行近似，相較于以上的濾波方法，CKF的精度和穩定性都有所提高，為解決非線性和噪聲不確定問題提供了一個新的起點。

以上方法均為非線性系統濾波常用的方法，但普遍存在跟蹤能力不強和自適應能力差的問題。在系統受到觀測值異常或者狀態量突變的影響時，濾波器容易產生精度下降的問題，甚至出現濾波發散的情況。文獻[6]提出了自適應CKF方法，能夠有效增強系統的跟蹤能力，系統的觀測值異常或狀態量突變問題也得到了很好地解決。文獻[8]提出了一種抗差方法，能夠有效減弱波動較大的數據對于濾波器穩定性的影響。

針對濾波跟蹤能力不強和自適應能力差的問題，提出了一種改進自適應抗差CKF算法，在自適應修正的基礎上使用抗差方法可以更好地減弱異常觀測值的影響，結合奇異值分解(Singular Value Decomposition，SVD)方法，可以使得濾波器更好地運行，改善了濾波效果，提高了濾波器的穩定性。

1 系統狀態方程和觀測方程

1.1 超寬帶測量方程

超寬帶(Ultra-Wide Band，UWB)測量方程可表示為

=()+

(1)

其中，=[,,…,]；=[,,]；(·)為觀測方程；=[,1,…,,]是零均值高斯測量誤差噪聲，其協方差矩陣為。

1.2 慣性導航系統測量方程

慣性導航系統(Inertial Navigation System，INS)測量模型，通過慣性測量單元(Interial Measurement Unit, IMU)傳感器的測量角速度和測量加速度獲取目標位姿信息，測量模型如下

=()+

(2)

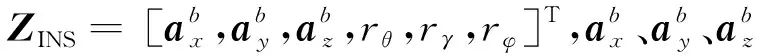
1.3 UWB/INS融合定位方程

非線性系統模型如下

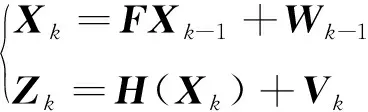
(3)

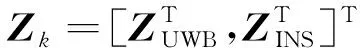
2 改進自適應抗差CKF算法

2.1 新息自適應修正

新息是實際值與量測預測值之差，能比較直觀地反映出預測值偏離實際狀態的趨勢與程度。新息一般用于對系統進行判定，并決定是否需要修正以及如何修正。

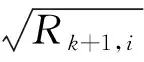
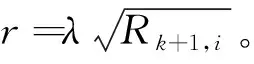
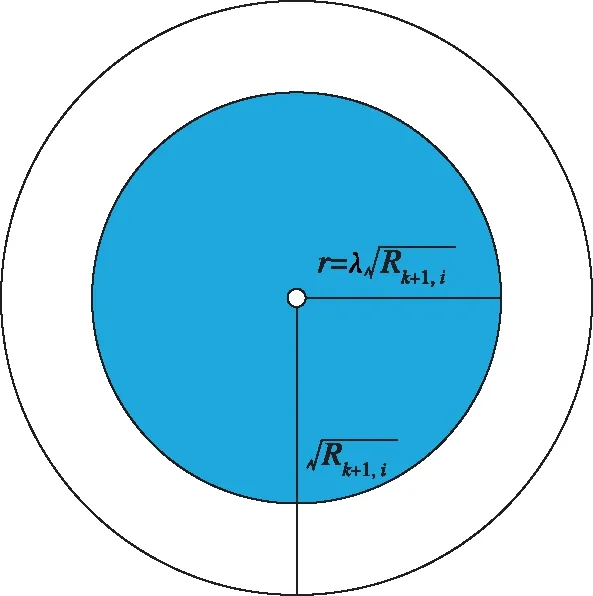
圖1 自適應修正判決門限

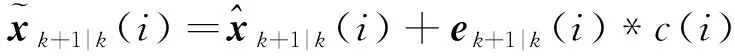
(4)

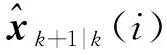
修正系數()的選取需要遵循適度修正原則，避免過度修正。主要考慮兩方面：一是修正系數與系統量測精度有關；二是與新息+1的維度有關。如新息中包含位置信息，位置信息對應的修正系數()可以選取稍大一些，不應超過0.01;速度的修正可以通過位置變化傳遞，則可以選取稍小些。

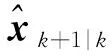
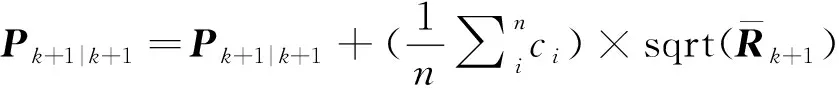
(5)

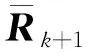
當新息小于判決門限時，則系統不要修正，按照CKF程序正常濾波即可。

2.2 抗差因子

在自適應修正的基礎上，引入抗差因子，減小異常觀測值對CKF過程的干擾。當觀測信息精度很高時，需加大觀測值在狀態估計中的權值；反之，當觀測信息誤差偏大時，需降低觀測值在狀態估計中的權重。

在系統得到新息之后，將新息進行標準化得到抗差

=,+1,+1

(6)

其中，,+1為新息的第個分量；,+1為其標準差。

類似IGGIII等價權函數模型，對觀測抗差值進行分類，分為3個等級進行篩選，分別對應三種不同的抗差因子

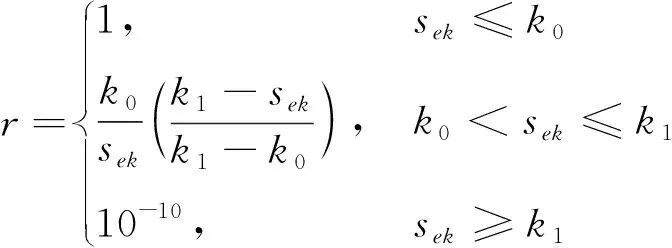
(7)

式中：、為常值，通常選取=15～20，=30～85；為標準化抗差。需要注意的是，抗差因子不能設置為0，否則可能會影響觀測向量協方差矩陣的迭代更新。

根據觀測抗差值引入抗差因子，對觀測噪聲協方差陣進行修正，即

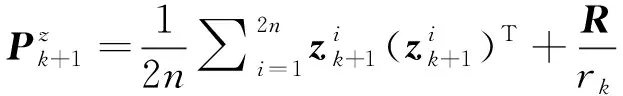
(8)

2.3 SVD

為了避免CKF算法中由于Cholesky分解導致的系統狀態協方差矩陣出現非正定的現象，可以采用SVD方式代替傳統的Cholesky分解。

SVD方法，定義如下：

假定∈×(≥)，則矩陣的SVD可以表示為

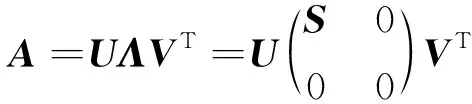
(9)

式中，∈×；∈×；∈×；=diag(,,…,)，≥≥…≥≥0。的列向量為矩陣的左奇異向量，的列向量為矩陣的右奇異向量。

2.4 改進的自適應抗差CKF算法

改進自適應抗差CKF算法步驟如下：

1)狀態參數初始化

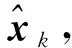
2)計算容積點

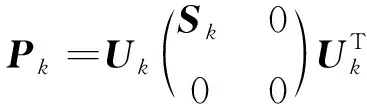
(10)

式中，為狀態量的維數，為容積點集，如下所示

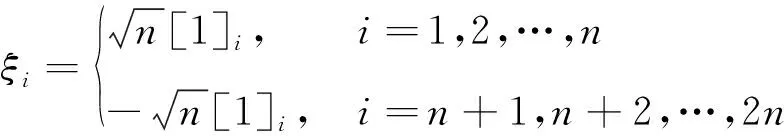
(11)

式中，[1]代表單位矩陣。

3)傳播容積點

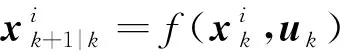
(12)

4)計算狀態量預測值及誤差協方差預測值

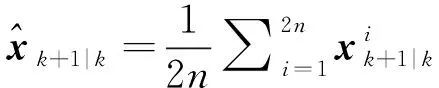
(13)

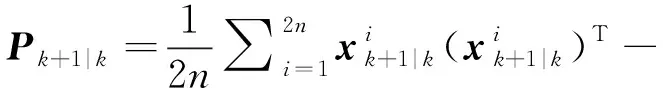
(14)

5)計算容積點

(15)

6)傳播容積點

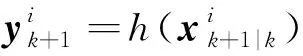
(16)

其中，為系統測量函數。

7)計算測量預測值

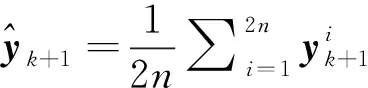
(17)

8)計算新息

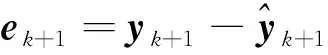
(18)

9)比較新息中的對應變量與門限值，進行狀態預測值修正

|+1|>

(19)

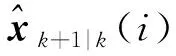
10)計算觀測預測協方差

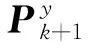
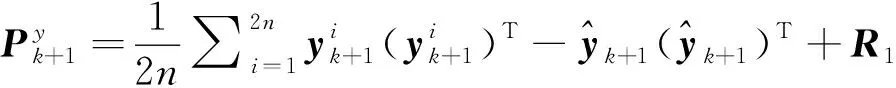
(20)

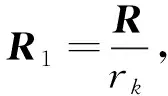
11)計算互協方差

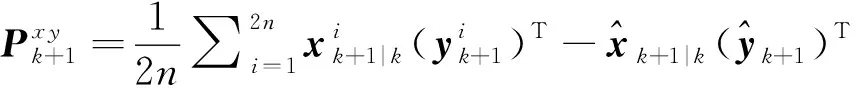
(21)

12)計算增益更新、狀態量、誤差協方差

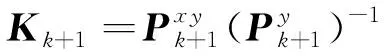
(22)

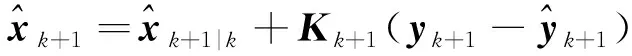
(23)

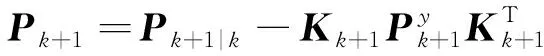
(24)

13)若式(4)執行，則需要根據式(5)估計誤差協方差陣進行補償；若不執行，則跳過式(5)。

3 實驗分析

本文設計了基于UWB與INS的融合定位仿真實驗，對自適應抗差CKF融合算法的魯棒性能進行評估。硬件由DWM1000模塊與IMU傳感器ADIS16465組成。實驗場地如圖2(a)所示。

在實驗環境中，4個基站高度相同均為2.05m。基站坐標為(3,0,2.05)，基站坐標為(3,3.9,2.05)，基站坐標為(0,3.9,2.05)，基站坐標為(0,0,2.05)，單位為m。UWB標簽與INS實際運動軌跡如圖2(b)所示，運行軌跡中設有障礙物，目的是有效驗證非視距處的UWB解算誤差情況。為了驗證算法的有效性，采用MATLAB進行仿真分析。

(a)

如圖3所示，在仿真過程中，UWB受到障礙物以及實際環境中噪聲干擾的影響，其結果在障礙物附近和起點處數據穩定性較差，整體穩定性較低。

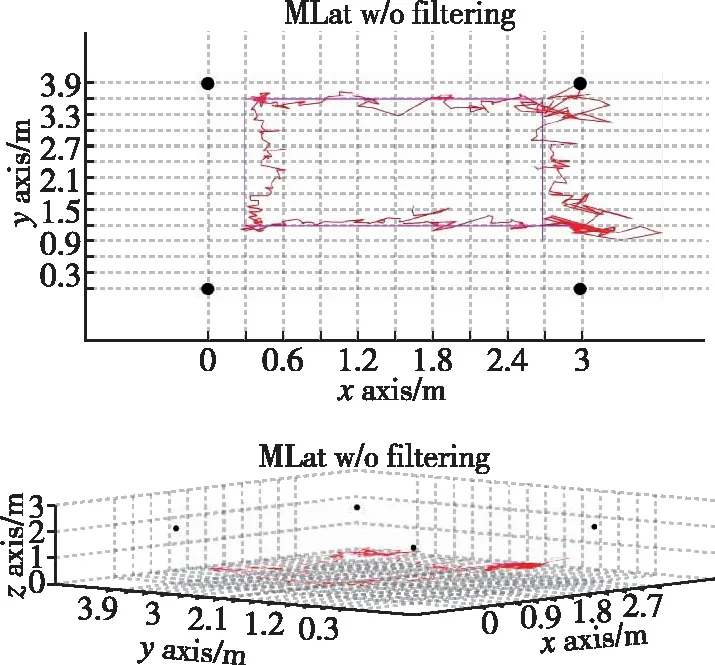
圖3 UWB定位結果

如圖4所示，將UWB與INS進行松耦合，結合改進自適應抗差CKF算法進行定位，在起點與障礙物處定位軌跡更加平滑、更接近實際運動軌跡。由此可以得出，該方法狀態估計更穩定，系統魯棒性更好。

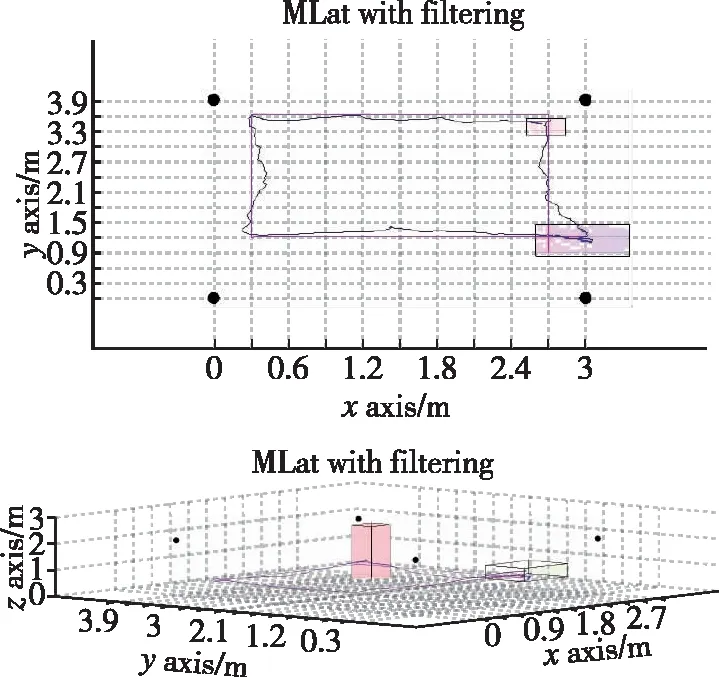
圖4 UWB/INS融合定位結果

同一場景下，對原始數據分別用EKF和CKF算法進行數據融合，并與改進自適應抗差CKF數據融合誤差情況進行對比。傳統EKF與CKF均降低了原始數據的整體誤差，平滑了誤差毛刺，提升了系統穩定性。如圖5所示，改進自適應抗差CKF算法與傳統EKF和CKF相比,進一步降低了系統整體誤差值，系統在0～100s和150～300s區間內效果最明顯。改進自適應抗差CKF與其他幾種濾波方法相比，精度更優，系統穩定性更好。

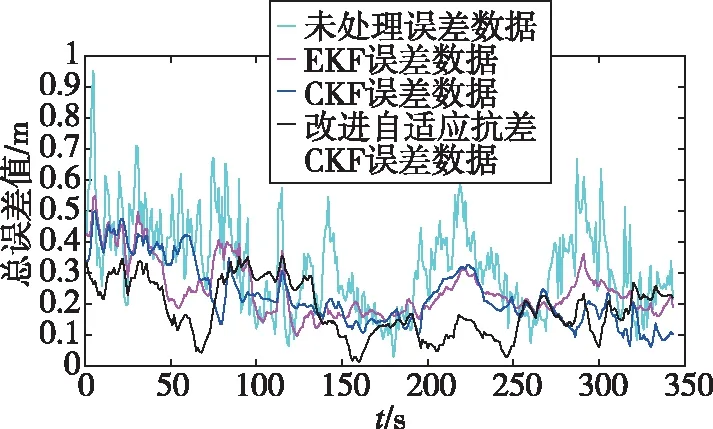
圖5 不同濾波方法數據融合誤差對比

各個濾波算法誤差數值分析如表1所示。可以看到，傳統CKF相較于EKF均值誤差降低了2.0451cm，而改進的方法較EKF均值誤差降低了6.8326cm。在此基礎上，所提方法最大誤差值相較于其他方法均有明顯降低，在系統出現異常時，減少了數值波動，進一步提升了系統穩定性。

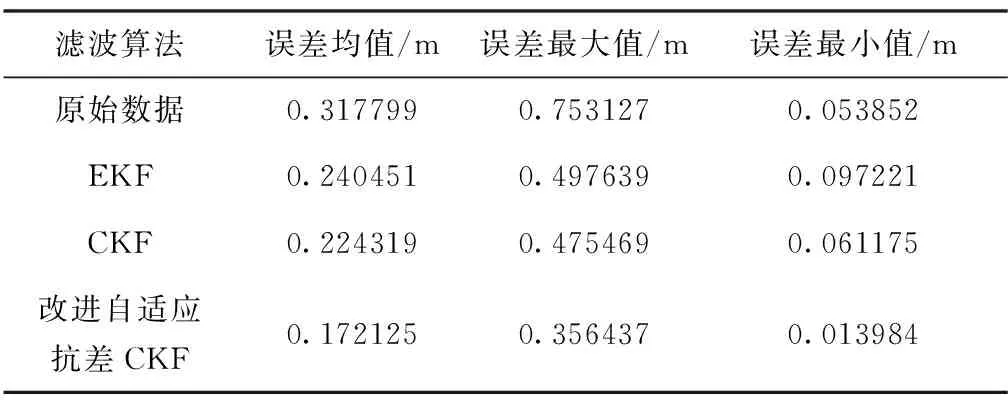
表1 不同濾波方法誤差數值情況對比表

4 結論

本文針對容積卡爾曼濾波在多源融合定位中存在跟蹤能力和自適應能力差的問題，采用改進的自適應抗差CKF算法進行仿真分析，并得到以下結論：

1)仿真結果表明，該算法能夠保持較高的濾波精度和數值穩定性。

2)改進的自適應抗差CKF算法相較于傳統EKF算法平均誤差降低了28.42%；相較于傳統CKF算法平均誤差降低了23.268%。加入的自適應修正和抗差因子減小了異常觀測值對傳統CKF的干擾，在障礙物附近處定位結果良好；用SVD代替CKF中的Cholesky分解，有效地提高了系統數值計算穩定性，增強了在粗差干擾下的魯棒性。因此，改進的自適應抗差CKF算法提高了多源融合定位精度。