基于知識“臨界點”培養數學結構化思維

林平芬（福建省龍巖市蓮東小學）

“臨界點”是物理學名詞，指物體由一種狀態變成另一種狀態前，應具備的條件。例如：水→冰→水蒸氣，因為能量不同而出現了相的改變，相的改變代表界的不同，這時，我們稱它為臨界了，而臨界時的值則稱為臨界點，后來人們用以形容事態發展的待變狀態。那么，我常想：在數學中，是否存在待變狀態，也就是“臨界點”呢？《基于核心素養的小學數學結構化思維培養》課題開展研究后，我發現“臨界點”在數學知識體系中不僅無處不在，還蘊含著豐富內涵，具有特殊性，只不過在教學中往往被忽略而已。

多年的教學實踐中，我從“臨界點”出發，引導學生去認識它，尋找它，理解它，運用它，從而引導學生逐步走向結構化思維的探索之路。

一、認識“界”，感受“界”之特殊

何為數學知識領域里的“臨界點”呢？我以下列說明：

張奠宙先生說：“首先要給出0，再談正負數。”把這句話轉化為數學符號語言：正數→0→負數，以“0”為界，就形成了一個數域的結構，如果放到數軸上，結構就一目了然了。（如圖一）

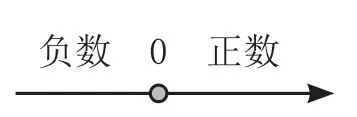
圖一

以“0”為界，形成數域結構后，我們再來解讀教材就更能理解編者的設計意圖了。人教版六年級下冊“認識負數”這單元，共有3個例題，例1以溫度引入課題，0°C表示淡水開始結冰的溫度，是零上溫度與零下溫度的分界點，這是自然意義規定的相反量；還有一種人為規定的分界，如教材中的例2、例3：例2從存折分析，收入為正，支出為負；例3以大樹為界，向東為正，向西為負；除此以外，如，以海平面為界（記作0），比海平面高記為正數，比海平面低記為負數；以商場為例，盈利為正、虧損為負；以產品質量標準如薯片200克為界（記作0），超出部分為正，不足部分為負，以北京時間為界（記作0），比它早為正，比它遲記為負……但無論是自然規定還是人為規定，正負數的分界點為0是無可厚非的。自然意義規定的“0”（如氣溫），學生是有體驗的，固定的、比較容易理解；而人為規定的“0”是變化的，學生的體驗不足，難度就增加了。但如果明確了“0”這個分界點的重要性，確定了0，再來談正負數，難度就降低了。

這樣，學生就能較好地認識“界”的真正內涵，并感受其特殊必性，從而形成數域結構，促進結構化思維的形成。

二、尋找“界”，發現“界”之所在

學生認識了“界”之后，在學習過程中，我們應該引導學生尋找更多的“臨界點”，并自主建構各種數學知識結構體系，努力促進學生結構化思維的形成。我是從以下三方面引領學生尋找“臨界點”的：

（一）從特殊點入手尋找

“特殊點”之所以特殊，就在于它的與眾不同。如“0”。我們知道，以“0”為界，可以區分正負，以“0”為界，點上“小數點”，還能把一個小數分成了整數部分、小數點和小數部分。0就是一個特殊點；還有“1”，以“1”為界，可以區分真假分數，比1大的分數，即分子比分母小的分數叫作真分數，比1大或等于1的分數，即分子比分母大或分子與分母相等的分數叫作假分數。以“1”為界，一個數，乘1，就得原數；一個數乘比1大的數，積就比原數大；一個數乘比1小的數，積就比原數小。同理，以“1”為界，一個數除以1，除以比1大的數、除以比1小的數，商也有一定的規律。以90°為界，可以對角進行分類：小于90°的是銳角、等于90°的是直角，大于90°小于180°的是鈍角，等于180度的是平角，等于360°的是周角，大于180°而小于360°的是優角……像這樣，數學知識領域里的特殊點比比皆是，在日常的數學學習中，我們如果能引導學生隨時關注各種“臨界點”，并迅速建立起各種知識結構，便能很好地掌握數學知識的本質特征，培養學生的結構化思維能力。

（二）從對比入手尋找

“臨界點”的核心特征是“相變”，那么，教師就應該引導學生觀察“相變”的過程，并對變化前后的數量關系、空間形式進行對比，便可尋找到“臨界點”之所在。“十進制”計數法是目前世界通用的計數法，1，2，3，4，5，6，7，8，9，當數到9時，再添上1就是10，數的表征從一位數變成了兩位數，即數由一個數字轉變為兩個數字組合而成。“10”就是一位數變為兩位數的分界點，這個特殊性如何引導學生發現并感知呢？教材里用數小棒的活動，1根、2根、…9根，當數到9根時，再添上一根是10根，把它們捆成一捆，課堂教學實踐中，教師需要引導學生思考：“為什么要捆成一捆呢？”“這一捆小棒可以表示什么？還可以表示什么呢？”學生操作時，10根“捆”成一捆的操作就賦予了“1個十”和“10個一”的含義，數出10根，捆成一捆，再拆開來，數一數，再捆成一捆，這樣反復操作，引導學生充分感知10個一等于1個十，1個十等于10個一，建構了“十進制”計數法的模型，為后續十位上的滿十進一、百位上的滿十進一、千位上的滿十進一……提供了有力的經驗，學生自然就能遷移應用。從“10”這個特殊的數字出發，感受十進制的進位“臨界點”的特殊性，是對后續學習“數與代數”領域知識具有深遠影響的關鍵生長點。

（三）從運動入手尋找

在《三角形》單元教學中，我在學生認識三角形并學會了分類后，設計了運用幾何畫板，讓學生在方格圖中通過運動，感受三角形頂點平移引起角的大小變化、引起三角形分類的變化、引起三角形高的位置的改變的探究。以直角形為界，我先固定了一個銳角三角形和一個直角三角形，再讓鈍角三角形隨著頂點D運動起來，截圖如下（圖二）：

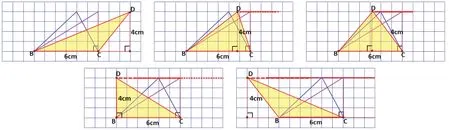
圖二

當鈍角三角形的頂點D平移運動起來后，我提出了三個問題：

鈍角三角形的頂點D平移運動時，什么變了，什么不變？

什么時候會變成直角三角形呢？以直角三角形為界，當點D走到哪兒時，變成銳角三角形？走到哪兒時又變成了鈍角三角形呢？

你還有什么發現嗎？

在討論第1個問題時，有的學生認為鈍角三角形的頂點D平移運動時，三角形的底邊不變，頂點D的位置變了，另外兩條邊的位置與大小隨之改變，所以三角形的角度、形狀都變了，有時是鈍角三角形，有時是直角三角形，有時是銳角三角形。

在討論第2個問題時，有的學生直觀指出，當三角形的高DB與邊DC重合時，就是直角三角形，只有這兩種情況。

當點D在底邊BC的正上方之間時，也就是高在三角形內，是銳角三角形；當D點移到線段BC的上方外時，這個三角形就變成了鈍角三角形。

在討論第3個問題“你還有什么發現？”時，學生說，在方格圖里，我可以清楚看見三角形的底不變，高的長度也不變，形狀不斷變化。

運用幾何畫板讓圖形運動起來，或旋轉，或平移，以問題驅動學生觀察、思考、分析，讓學生能直觀地看明白，以直角三角形的直角邊為界，頂點處在不同的位置，三角形的類型就不同，特別是鈍角三角形，頂點離底邊越遠，高就離底邊越遠，鈍角就越大，形狀變化就越大，同時，學生經歷了“三角形等積變形”的形成過程，明確了直角三角形是形變的“臨界點”之所在，從而便自主地建構起知識結構，培養了學生的結構化思維。

像這樣在運動中尋找“臨界點”的方法，在“圖形與幾何”領域的教學中常常適用。如：兩條直線在同一平面內的位置關系：相交與垂直，運用幾何畫板，在運動中可以使學生深度理解，在同一平面內，垂直是兩條直線相交的一種特殊情況，以它為界，其余的相交都不會成直角，只能稱為相交；角的分類也可以，在運動中，以直角為“臨界點”，可以迅速幫助學生建立角的類別知識結構。像這樣的例子還有很多，在運動國尋找“臨界點”，不僅可以幫助學生建構“圖形與幾何”領域的知識結構，更有利于培養學生的空間觀念。

三、理解界，明晰界之關聯

建立了界以后，理解界之關聯是需要老師下大功夫的。如何理解界之關聯呢？數形結合與問題驅動乃是良策。

（一）以表助解，界中晰聯

數學家華羅庚說：“數形結合百般好，隔離分家萬事休。”無論是“數與代數”領域，還是“圖形與幾何”領域，均可應用數形結合思想，用畫圖、列表等方式，幫助學生理解“臨界點”，明確界之關聯。

以人教版五年級上冊“質數與合數”為例：質數的概念是一個數，如果只有1和它本身兩個因數，這樣的數就叫作質數；合數的概念是一個數，如果除了1和它本身還有別的因數，這樣的數叫作合數。那么根據這兩個概念，一個數所含的因數數量是判斷一個數是質數還是合數的要點，它們的分界點就在2個因數上。為了方便理解，我們可以做成下面的表格（如圖三）：

圖三

通過上面的列表分析，可以清晰地看出整數1為什么既不是質數，也不是合數，因為它的因數數量最特別，只有1個。而質數是兩個，合數的因數數量是2個以上，即3個、4個、5個……通過列表，可以使學生更為清晰地理解質數與合數的界在何處，是怎樣建立的，這樣的方式形成的數的分類結構是有框架的，有源可溯，有據可依的，用這樣的方式建立的概念模型是關聯的，牢不可破的。

（二）以形助解，融中建聯

除了列表之外，數形結合的強大力量是人盡皆知的，我們要想盡辦法，將它融入課堂教學中。以人教版四年級上冊“角的度量”為例，我畫出這樣一條線段（如圖四）：

圖四

你認為上圖中的（ ）點可能是（ ）角，大約是（ ）°，理由是：（ ）。

這樣的設計，把角的分類知識放到線段上，在0o~360o之間，設置不同的點，將數與形結合，引導學生說理，培養學生的數感與量感，滲透了數形結合、化曲為直的數學思想。其中B點表示的約是90°，是直角，它是一個“分界點”，具有參照作用。

理解界，以列表、數形結合等方式分析“界”與“界”之間的關聯，明確“界”形成的原因，有助于結構的形成，促進學生結構化思維的培養。

四、運用“界”，實施“界”之本質

學生建立起“臨界點”的概念后，就需要有意識地引導他們運用這一知識本質特征去解決問題。如在《三角形》單元教學中，學生運用幾何畫板建立了“三角形的等積變形”模型后，明確了三角形分類的“臨界點”后，我設計了這樣一道選擇題：

如右圖（圖五），平行四邊形內有一個三角形ABC，已知它的面積是18平方分米，那么陰影部分的面積是（ ）平方分米。

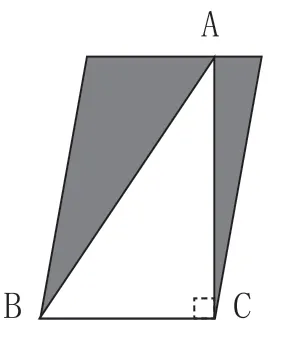
圖五

此題只給了一個信息：三角形的面積是18平方分米，要求的是陰影部分的面積是多少平方分米？而陰影部分是由兩個三角形組成的，它們的底和高的大小均未知，所以感覺本題有一定的難度。但在我執教的《三角形面積的再認識》一課中，因為學生在圖形的“運動”中建立了關于“臨界點”的知識結構，有近60%的學生馬上給出了答案為C。他們的想法如圖六所示，將三角形ABC的頂點A沿著平行四邊形的上邊平移，移至對角的位置，這時三角形ABC的面積就是平行四邊形的一半，也與原來的面積相等（同底等高），所以陰影部分的面積就是三角形ABC的面積。

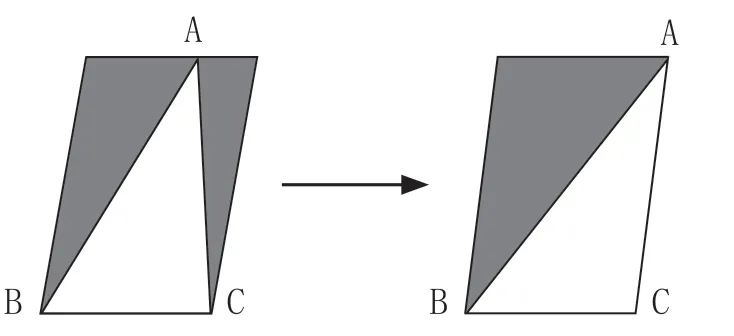
圖六

又如，在五年級上冊《異分母分數的加減法》一課中，我出了這樣一道單項選擇題：

下列各式中，（ ）的和大于1。

由此可見，一旦學生認識了“臨界點”，形成了尋找“臨界點”的習慣，知識結構的形成就水到渠成了。當他們在學習中遇到困難時，就能自主探索，自覺實踐，形成運用“臨界點”來解決問題的思考方式，日積夜累，長此以往，他們就逐漸從“臨界點”走向了結構化思維。