三關(guān)節(jié)位姿約束單驅(qū)動(dòng)非圓齒輪五桿手指機(jī)構(gòu)研究

葉 軍 陳建能 喻陳楠 沈姍姍 薛明瑞 葉志超

(1.浙江工業(yè)職業(yè)技術(shù)學(xué)院機(jī)電工程學(xué)院， 紹興 312000; 2.浙江理工大學(xué)機(jī)械與自動(dòng)控制學(xué)院， 杭州 310018)

0 引言

仿生手指機(jī)構(gòu)是拾取機(jī)器人和人體假手的重要組成部分，并廣泛地運(yùn)用于生產(chǎn)和生活實(shí)踐中。為了適應(yīng)不同的需求，學(xué)者們?cè)O(shè)計(jì)了多種構(gòu)型和驅(qū)動(dòng)方式的仿生手指機(jī)構(gòu)[1-3]。由于手指關(guān)節(jié)數(shù)量、緊湊性等限制，仿生手指各關(guān)節(jié)無(wú)法進(jìn)行單獨(dú)驅(qū)動(dòng)，為此欠驅(qū)動(dòng)機(jī)構(gòu)和單驅(qū)動(dòng)機(jī)構(gòu)常常被用于設(shè)計(jì)仿生手指機(jī)構(gòu)。李小彭等[4]基于變胞原理提出了一種欠驅(qū)動(dòng)仿生手，3個(gè)關(guān)節(jié)可以實(shí)現(xiàn)2種不同的工作模式。劉今越等[5]提出了一種關(guān)節(jié)可鎖緊的單腱欠驅(qū)動(dòng)機(jī)構(gòu)，并完成手指?jìng)鲃?dòng)機(jī)構(gòu)和腱繩張緊機(jī)構(gòu)的設(shè)計(jì)。SUN等[6]通過(guò)齒輪、桿組和彈簧組成一個(gè)欠驅(qū)動(dòng)手指機(jī)構(gòu)，能夠較好地完成耦合和自適應(yīng)抓取物體。欠驅(qū)動(dòng)手指機(jī)構(gòu)多采用腱繩驅(qū)動(dòng)方式[7]，使得手指機(jī)構(gòu)的承載能力、穩(wěn)定性和精度等都有所降低。

傳統(tǒng)單驅(qū)動(dòng)機(jī)構(gòu)具有承載能力高、精度好、控制簡(jiǎn)單等特點(diǎn)，近幾年越來(lái)越多學(xué)者將其運(yùn)用于手指機(jī)構(gòu)設(shè)計(jì)中。BATALLER等[8]采用八桿機(jī)構(gòu)設(shè)計(jì)了手指外骨骼機(jī)構(gòu)，并將其用于手指康復(fù)訓(xùn)練中。JANG等[9]采用可堆疊的雙四桿機(jī)構(gòu)設(shè)計(jì)了單驅(qū)動(dòng)的仿生食指機(jī)構(gòu)并進(jìn)行了運(yùn)動(dòng)學(xué)分析。LIU等[10]采用五桿周轉(zhuǎn)機(jī)構(gòu)設(shè)計(jì)了具有高承載能力的仿生手指機(jī)構(gòu)并進(jìn)行了相關(guān)試驗(yàn)。GUI[11]提出了基于肢體運(yùn)動(dòng)識(shí)別的單驅(qū)動(dòng)八桿機(jī)構(gòu)設(shè)計(jì)方法，并將其用于手指機(jī)構(gòu)設(shè)計(jì)中。韓建友等[12-13]提出了基于解域綜合的單驅(qū)動(dòng)平面六桿和八桿手指機(jī)構(gòu)設(shè)計(jì)方法，并依據(jù)力傳遞性能選取了最佳參數(shù)。然而現(xiàn)有傳統(tǒng)單驅(qū)動(dòng)多桿手指機(jī)構(gòu)的結(jié)構(gòu)緊湊性不夠，同時(shí)大多數(shù)機(jī)構(gòu)無(wú)法實(shí)現(xiàn)人類(lèi)手指關(guān)節(jié)運(yùn)動(dòng)中的位置和姿態(tài)(以下稱(chēng)位姿)要求。

針對(duì)上述分析的問(wèn)題，本文提出一種基于三關(guān)節(jié)位姿約束的單驅(qū)動(dòng)非圓齒輪五桿手指機(jī)構(gòu)設(shè)計(jì)方法，以期使得仿手指機(jī)構(gòu)更好地實(shí)現(xiàn)人類(lèi)手指在運(yùn)動(dòng)中的位姿要求。

1 單驅(qū)動(dòng)非圓齒輪五桿手指機(jī)構(gòu)組成和求解思路

圖1為單驅(qū)動(dòng)非圓齒輪五桿手指機(jī)構(gòu)，由一對(duì)非圓齒輪副和五桿機(jī)構(gòu)組成。其中，非圓齒輪1為固定中心輪，非圓齒輪2中心安裝于鉸鏈點(diǎn)A處，并與桿AB保持固定聯(lián)結(jié)，五桿機(jī)構(gòu)OABCD通過(guò)鉸鏈點(diǎn)O安裝于機(jī)架上。該機(jī)構(gòu)原理為：驅(qū)動(dòng)桿OD在普通電機(jī)驅(qū)動(dòng)下相對(duì)于機(jī)架轉(zhuǎn)動(dòng)，從而驅(qū)動(dòng)非圓齒輪2繞著非圓齒輪1做行星運(yùn)動(dòng)，并進(jìn)一步帶動(dòng)連桿AB做平面運(yùn)動(dòng)，最終實(shí)現(xiàn)整體機(jī)構(gòu)進(jìn)行平面仿手指運(yùn)動(dòng)。相比較于圖2所示的六桿手指機(jī)構(gòu)，該機(jī)構(gòu)采用齒輪機(jī)構(gòu)具有更好的緊湊性和傳力性，同時(shí)非圓齒輪副傳動(dòng)的多樣性賦予了該機(jī)構(gòu)更高的設(shè)計(jì)靈活性。最佳仿生手指機(jī)構(gòu)能夠完全實(shí)現(xiàn)人類(lèi)的手指運(yùn)動(dòng)位置和姿態(tài)要求，為此本文中以三關(guān)節(jié)位姿為約束，建立非圓齒輪五桿機(jī)構(gòu)運(yùn)動(dòng)綜合方法，最大限度地實(shí)現(xiàn)人類(lèi)手指運(yùn)動(dòng)中的位置和姿態(tài)要求。

圖1 單驅(qū)動(dòng)非圓齒輪五桿手指機(jī)構(gòu)組成Fig.1 Composition of 1-DOF non-circular gear five bar finger mechanism1、2.非圓齒輪副 3.驅(qū)動(dòng)桿OD 4.連桿AB 5.末端桿BP 6.連桿DC

圖2 六桿手指機(jī)構(gòu)組成Fig.2 Composition of six bar finger mechanism1.連架桿O1E 2.驅(qū)動(dòng)桿OD 3.連桿AC 4.連桿AB 5.末端桿BP 6.連桿DC

本文單驅(qū)動(dòng)非圓齒輪五桿手指機(jī)構(gòu)求解思路為：首先選取三關(guān)節(jié)的若干個(gè)位姿作為初始約束條件，如圖3a所示。以給定的三關(guān)節(jié)位姿為約束，求解滿(mǎn)足約束條件要求的鉸鏈點(diǎn)A和B參數(shù)，得到一個(gè)五桿機(jī)構(gòu)，如圖3b所示。最后，根據(jù)驅(qū)動(dòng)桿OD和連桿AB的轉(zhuǎn)角關(guān)系，求解滿(mǎn)足給定三關(guān)節(jié)位姿要求的非圓齒輪副，得到單驅(qū)動(dòng)非圓齒輪五桿手指機(jī)構(gòu)，如圖3c所示。

圖3 單驅(qū)動(dòng)非圓齒輪五桿手指機(jī)構(gòu)求解思路Fig.3 Solution idea of 1-DOF non-circular gear five bar finger mechanism1、2.非圓齒輪 3.驅(qū)動(dòng)桿OD 4.連桿AB 5.未端桿BP 6.連桿DC

2 三關(guān)節(jié)位姿約束的非圓齒輪五桿機(jī)構(gòu)設(shè)計(jì)方法

2.1 三關(guān)節(jié)位姿約束的運(yùn)動(dòng)映射建立

圖4 五桿機(jī)構(gòu)示意圖Fig.4 Schematic of five bar mechanism

圖4為五桿機(jī)構(gòu)示意圖，在鉸鏈點(diǎn)O建立動(dòng)坐標(biāo)系X2UY2并隨著驅(qū)動(dòng)桿OD運(yùn)動(dòng)而運(yùn)動(dòng)，在五桿機(jī)構(gòu)的位姿點(diǎn)P上建立動(dòng)坐標(biāo)系X3EY3并隨著連桿CP運(yùn)動(dòng)。當(dāng)給定三關(guān)節(jié)的若干位姿為約束條件時(shí)，即已知五桿機(jī)構(gòu)桿OD、DC、CP長(zhǎng)度以及若干個(gè)運(yùn)動(dòng)位姿，只需求解出鉸鏈點(diǎn)A和B坐標(biāo)位置就可得到滿(mǎn)足三關(guān)節(jié)位姿約束的五桿機(jī)構(gòu)。

通過(guò)三關(guān)節(jié)約束位姿條件可知鉸鏈點(diǎn)O的安裝位置O(a,b)、第一桿OD的轉(zhuǎn)角φ1(逆時(shí)針為正)、末端位置點(diǎn)P(g,h)以及方位角φ2，為此第一坐標(biāo)系X1OY1下位姿點(diǎn)P(g,h)在第二坐標(biāo)系X2UY2中點(diǎn)P(e,f)表示為

(1)

其中

υ=φ1-φ2

j1=(g-a)cosφ1-(b-h)sinφ1
j2=(h-b)cosφ1+(a-g)sinφ1

由圖4可知，鉸鏈點(diǎn)D和A在動(dòng)坐標(biāo)系X2UY2為定點(diǎn)，因此在動(dòng)坐標(biāo)系X2UY2下，該五桿機(jī)構(gòu)就等效為圖5所示的四桿機(jī)構(gòu)。因此，在已知若干三關(guān)節(jié)(即桿OD、DC和CP三關(guān)節(jié))位姿時(shí)，求解五桿機(jī)構(gòu)未知鉸鏈點(diǎn)A和B的問(wèn)題，可通過(guò)式(1)轉(zhuǎn)換成為已知桿DC和桿CP若干位姿的2R桿組運(yùn)動(dòng)綜合求解問(wèn)題。

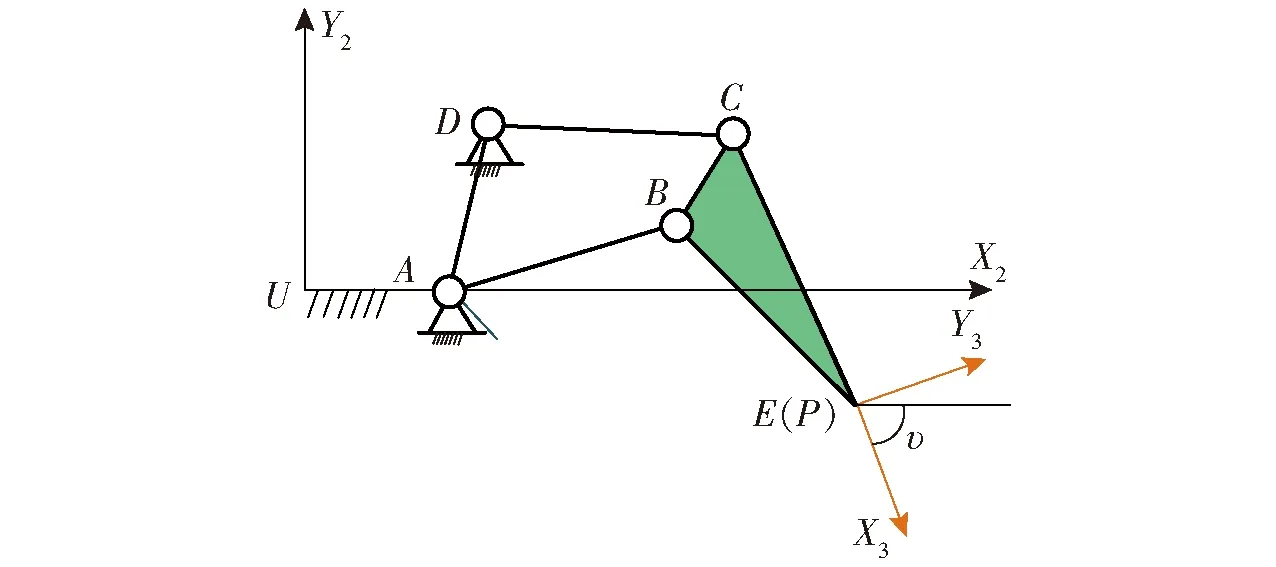
圖5 在動(dòng)坐標(biāo)系X2UY2中的四桿機(jī)構(gòu)Fig.5 Four bar mechanism in dynamic coordinate system X2UY2

根據(jù)剛體運(yùn)動(dòng)學(xué)映射相關(guān)理論[14-15]，第二坐標(biāo)系X2UY2下的末端位姿點(diǎn)P(e，f，v)可采用齊次坐標(biāo)(Z1，Z2，Z3，Z4)進(jìn)行表達(dá)，具體為

(2)

由于動(dòng)坐標(biāo)系X3EY3建立在位姿點(diǎn)P上并隨桿CP運(yùn)動(dòng)，那么五桿機(jī)構(gòu)中的坐標(biāo)點(diǎn)B在動(dòng)坐標(biāo)系X3EY3下為定點(diǎn)B(x,y)，在第二坐標(biāo)系X2UY2下點(diǎn)B坐標(biāo)(XB，YB)可以表示為

(3)

即

(4)

2.2 五桿機(jī)構(gòu)運(yùn)動(dòng)綜合求解

由圖5可知，在第二坐標(biāo)系X2UY2下點(diǎn)B(XB，YB)被約束在以點(diǎn)A為圓心、桿AB為半徑的圓周上，為此點(diǎn)B的平面運(yùn)動(dòng)軌跡可以表示為

(5)

其中a0、a1、a2、a3為圓的參數(shù)，a0≠0。

將式(5)用動(dòng)坐標(biāo)系X3EY3下的定點(diǎn)B(x,y)進(jìn)行表示，即將式(4)代入式(5)可得

(6)

式(6)中，令p1=2a0，p2=-2a0x，p3=-2a0y，p4=2a1，p5=2a2，p6=2(a2x-a1y)，p7=-(a1x+a2y)，p8=0.5(a3+a0x2+a0y2)，通過(guò)公式整理可得

(7)

通過(guò)幾何關(guān)系可以求解動(dòng)坐標(biāo)系X3EY3下的定點(diǎn)B(x,y)為

(8)

并可通過(guò)式(3)得到第二坐標(biāo)系X2UY2下坐標(biāo)點(diǎn)B(XB，YB)。

通過(guò)式(5)中圓心點(diǎn)的求解，得到第二坐標(biāo)系X2UY2下坐標(biāo)點(diǎn)A(XA，YA)為

(9)

2R桿組夾角為

(10)

式中φ1——第二坐標(biāo)系下第二桿AB和水平線(xiàn)之間的夾角

φ2——第二坐標(biāo)系下第三桿BC和水平線(xiàn)之間的夾角

由式(8)、(9)可知，只要求解出pi(i=1,2，…，8)可最終得到滿(mǎn)足三關(guān)節(jié)約束的五桿機(jī)構(gòu)參數(shù)。當(dāng)給定n組三關(guān)節(jié)位姿約束條件，最終通過(guò)式(6)得到一個(gè)過(guò)約束的線(xiàn)性方程組

(11)

其中

對(duì)于一個(gè)過(guò)約束線(xiàn)性方程組，主要采用方法有QR分解法、高斯消元法以及奇異值分解法(SVD)等數(shù)學(xué)方法。為了求解最小二乘法意義上的一般解空間，本文采用奇異值分解法求解線(xiàn)性方程組，滿(mǎn)足式(7)所示的附加約束條件的特定值。由于pMTMp=0，該線(xiàn)性方程組求解問(wèn)題變?yōu)榍蠼釳TM的特征向量V的問(wèn)題。根據(jù)奇異值分解過(guò)程，將求解出MTM的單位特征向量按特征值由小到大排列為v1,v2,…,v8。設(shè)α,β,γ,…,δ為若干系數(shù)，則一般解空間為

p=αv1+βv2+γv3+…+δv8

(12)

為了求解第二坐標(biāo)系X2UY2下的桿AB，至少要選取3個(gè)單位特征向量，式(7)的兩個(gè)約束條件(方程組)才有解。對(duì)于過(guò)約束的方程組(即存在4組約束條件以上)，必然存在著誤差，而特征值反映了誤差，為此本文選取4個(gè)最小的單位特征向量，組成解空間為

q=αv1+βv2+γv3+κv4

(13)

將式(12)代入到式(7)中進(jìn)行求解時(shí)，需要對(duì)其中的一個(gè)參數(shù)進(jìn)行賦值處理，即

κ=cotω(ω∈(0,π))

(14)

通過(guò)上述的計(jì)算過(guò)程，可以得到第二坐標(biāo)系X2UY2下桿AB的鉸鏈點(diǎn)A和B曲線(xiàn)，再通過(guò)式(1)求解在第一坐標(biāo)系X1OY1下的鉸鏈點(diǎn)A和B曲線(xiàn)，如圖6所示。在曲線(xiàn)上選取對(duì)應(yīng)點(diǎn)得到鉸鏈點(diǎn)A和B的坐標(biāo)值，并以第一個(gè)位置點(diǎn)機(jī)構(gòu)參數(shù)為五桿機(jī)構(gòu)的最終參數(shù)。

圖6 五桿機(jī)構(gòu)鉸鏈點(diǎn)A和B曲線(xiàn)示意圖Fig.6 Schematic of hinge points A and B curves of five bar mechanism

當(dāng)三關(guān)節(jié)位姿約束條件大于4組時(shí)，所求的五桿機(jī)構(gòu)無(wú)法精確實(shí)現(xiàn)所有位姿點(diǎn)，存在著一定誤差。在第二坐標(biāo)系X2UY2下，誤差出現(xiàn)在桿AB和BP求解過(guò)程中，而位姿點(diǎn)P在三關(guān)節(jié)位姿約束時(shí)的位置為

(15)

式中l(wèi)AB——桿AB的長(zhǎng)度lBP——桿BP的長(zhǎng)度

該五桿機(jī)構(gòu)誤差是實(shí)際位姿點(diǎn)位置與目標(biāo)位置點(diǎn)之間的誤差，為此各點(diǎn)誤差和平均誤差為

(16)

式中L1i——各點(diǎn)誤差em——平均誤差

2.3 位姿約束要求的非圓齒輪模型建立

由圖1和圖3可知，單驅(qū)動(dòng)非圓齒輪五桿機(jī)構(gòu)是由非圓齒輪配合完成具體的平面運(yùn)動(dòng)，因此需要設(shè)計(jì)滿(mǎn)足三關(guān)節(jié)位姿約束的非圓齒輪副。由于非圓齒輪單方向轉(zhuǎn)動(dòng)，需要先判定與齒輪旋轉(zhuǎn)相關(guān)兩桿是否符合齒輪傳動(dòng)要求。由于三關(guān)節(jié)位姿約束條件是給定的，桿OA的轉(zhuǎn)動(dòng)方向已知，需判定桿AB相對(duì)于桿OA的順序缺陷，即判定坐標(biāo)系X2UY2中式(10)中所得轉(zhuǎn)角φ1是否滿(mǎn)足轉(zhuǎn)動(dòng)順序和方向。順序缺陷的判定方法即為判別轉(zhuǎn)角φ1是否按從小到大進(jìn)行排列。

由具體結(jié)構(gòu)可知，非圓齒輪副的作用是實(shí)現(xiàn)連桿OA和連桿AB之間的轉(zhuǎn)角關(guān)系，為此需構(gòu)造兩桿之間的傳動(dòng)關(guān)系。根據(jù)2.2節(jié)的五桿機(jī)構(gòu)運(yùn)動(dòng)綜合求解，可以得到坐標(biāo)系X1O1Y1中若干個(gè)桿OA轉(zhuǎn)角θ1i(i=0,1,…,n)和桿AB轉(zhuǎn)角θ2i，所構(gòu)造的兩桿傳動(dòng)關(guān)系必須經(jīng)過(guò)這些對(duì)應(yīng)點(diǎn)，本文通過(guò)三次樣條曲線(xiàn)進(jìn)行插值擬合構(gòu)造兩桿轉(zhuǎn)角關(guān)系為

θ2=G(θ1)

(17)

具體的過(guò)程詳見(jiàn)文獻(xiàn)[16]。

根據(jù)上述所得轉(zhuǎn)角關(guān)系曲線(xiàn)，可以計(jì)算得到非圓齒輪副傳動(dòng)比為

(18)

為此，在已知桿OA長(zhǎng)度為2a和非圓齒輪傳動(dòng)比函數(shù)時(shí)，根據(jù)非圓齒輪傳動(dòng)原理，主動(dòng)齒輪、從動(dòng)齒輪的節(jié)曲線(xiàn)方程為[17-19]

(19)

3 單驅(qū)動(dòng)非圓齒輪五桿手指機(jī)構(gòu)的IO方程

建立單驅(qū)動(dòng)非圓齒輪五桿手指機(jī)構(gòu)的IO方程，便于研究該機(jī)構(gòu)末端連桿的軌跡和姿態(tài)，分析手指機(jī)構(gòu)的運(yùn)動(dòng)學(xué)特性。

圖7為單驅(qū)動(dòng)非圓齒輪五桿手指機(jī)構(gòu)運(yùn)動(dòng)簡(jiǎn)圖。設(shè)桿OA與水平夾角為ψ1，桿AD與桿AB夾角為ψ2，桿AD與桿DC夾角為ψ3。

圖7 單驅(qū)動(dòng)非圓齒輪五桿機(jī)構(gòu)的運(yùn)動(dòng)簡(jiǎn)圖Fig.7 Kinematic diagram of 1-DOF non-circular gear five bar finger mechanism

由上述的單驅(qū)動(dòng)非圓齒輪五桿機(jī)構(gòu)綜合，可以得到該機(jī)構(gòu)的具體結(jié)構(gòu)參數(shù)以及初始條件。設(shè)co、ca、cb、cc、cd、cp分別是鉸鏈點(diǎn)O、A、B、C、D以及末端點(diǎn)P的坐標(biāo)。當(dāng)該機(jī)構(gòu)的輸入轉(zhuǎn)角為ψ1時(shí)，可以得到鉸鏈點(diǎn)A和D的坐標(biāo)為

(20)

式中l(wèi)OA——桿OA長(zhǎng)度lOD——桿OD長(zhǎng)度

η1——固定夾角∠DOA

而根據(jù)非圓齒輪傳動(dòng)原理和式(17)可知

ψ2-ψ20=G(ψ1-ψ10)

(21)

式中ψ10、ψ20——初始安裝角度

在圖7中四桿機(jī)構(gòu)ABCD的任意一個(gè)位姿，都可通過(guò)Freudenstein方程將四桿機(jī)構(gòu)ABCD中的輸入與輸出之間寫(xiě)成無(wú)量綱形式[20]

k1-k2cosψ2-k3cosψ3+
cosψ3sinψ2-cosψ2sinψ3=0

(22)

其中

(23)

式中k1、k2、k3——參數(shù)

計(jì)算得到ψ3，由此可以計(jì)算得到鉸鏈點(diǎn)C和B坐標(biāo)為

(24)

其中

為此，最終位姿點(diǎn)P的坐標(biāo)為

cp=cc+R(η2)2lCP

(25)

其中

式中η2——固定夾角∠PCB

根據(jù)上述過(guò)程，可以建立輸入桿OA轉(zhuǎn)角與位姿點(diǎn)P之間的IO方程。

4 設(shè)計(jì)實(shí)例與試驗(yàn)

根據(jù)相關(guān)文獻(xiàn)中的人體手指長(zhǎng)度，選擇約50百分位手指尺寸作為樣本，具體如表1所示。以掌指關(guān)節(jié)為原點(diǎn)并通過(guò)試驗(yàn)數(shù)據(jù)得到手指在平面內(nèi)運(yùn)動(dòng)軌跡，從中取整并提取了5個(gè)三關(guān)節(jié)處轉(zhuǎn)角值(表2)，末端位姿點(diǎn)可由此轉(zhuǎn)角和手指尺寸計(jì)算得到。該手指機(jī)構(gòu)是以第一桿轉(zhuǎn)角、末端位姿點(diǎn)、安裝原點(diǎn)為初始條件，構(gòu)建滿(mǎn)足三關(guān)節(jié)位姿約束的五桿機(jī)構(gòu)，然后求解滿(mǎn)足約束要求的非圓齒輪副。

表1 人體手指長(zhǎng)度選取Tab.1 Selection of human finger length

表2 三關(guān)節(jié)的5個(gè)轉(zhuǎn)動(dòng)角Tab.2 Five rotation angle of three finger joints (°)

首先將5個(gè)末端位姿點(diǎn)通過(guò)式(1)轉(zhuǎn)換為動(dòng)坐標(biāo)X2UY2下的坐標(biāo)點(diǎn)，構(gòu)建求解鉸鏈點(diǎn)A和B的系數(shù)矩陣，并由矩陣奇異值分解方法得到如表3所示特征值，并根據(jù)2.2節(jié)最終求解出鉸鏈點(diǎn)A和B曲線(xiàn)，如圖8所示。

表3 給定的5個(gè)位姿點(diǎn)的特征值Tab.3 Eigenvalues of five position and pose points

為了得到合適的手指桿機(jī)構(gòu)結(jié)構(gòu)參數(shù)，將鉸鏈點(diǎn)A的選取限定在一定的范圍之內(nèi)(xA∈[12 mm,25 mm]，yA∈[-10 mm，8 mm])，并限定40 mm≤lAB≤50 mm，10 mm≤lBC≤20 m。在限定范圍內(nèi)，通過(guò)順序缺陷、桿長(zhǎng)判定等其他約束條件得到最終可行解域，如圖9所示。

圖9 鉸鏈點(diǎn)A和鉸鏈點(diǎn)B的可行解域Fig.9 Feasible solution domain of hinge points A and B

選取鉸鏈點(diǎn)A為(15.13，-1.21)mm，鉸鏈點(diǎn)B為(60.47,13.69)mm，計(jì)算得到連桿OA和連桿AB的轉(zhuǎn)角，再由三次樣條曲線(xiàn)構(gòu)建非圓齒輪副的傳動(dòng)比曲線(xiàn)，如圖10所示。通過(guò)連桿OA長(zhǎng)度以及傳動(dòng)比曲線(xiàn)，計(jì)算得到非圓齒輪節(jié)曲線(xiàn)并構(gòu)造齒輪輪廓，如圖11所示。根據(jù)上文中單驅(qū)動(dòng)非圓齒輪五桿手指機(jī)構(gòu)的IO方程，運(yùn)用Matlab軟件進(jìn)行編程計(jì)算得到圖12 所示的手指機(jī)構(gòu)位姿點(diǎn)P運(yùn)動(dòng)軌跡，其中該機(jī)構(gòu)位姿點(diǎn)位置誤差為0.236 mm，無(wú)姿態(tài)誤差。

圖10 非圓齒輪副的傳動(dòng)比Fig.10 Transmission ratio of non-circular gear pair

圖11 非圓齒輪副齒廓Fig.11 Tooth profile of non-circular gear pair

圖12 手指機(jī)構(gòu)的末端運(yùn)動(dòng)軌跡Fig.12 End motion trajectory of finger mechanism

根據(jù)上述機(jī)構(gòu)尺寸參數(shù)，采用Creo軟件建立三維模型，得到如圖13所示的手指機(jī)構(gòu)三維模型。

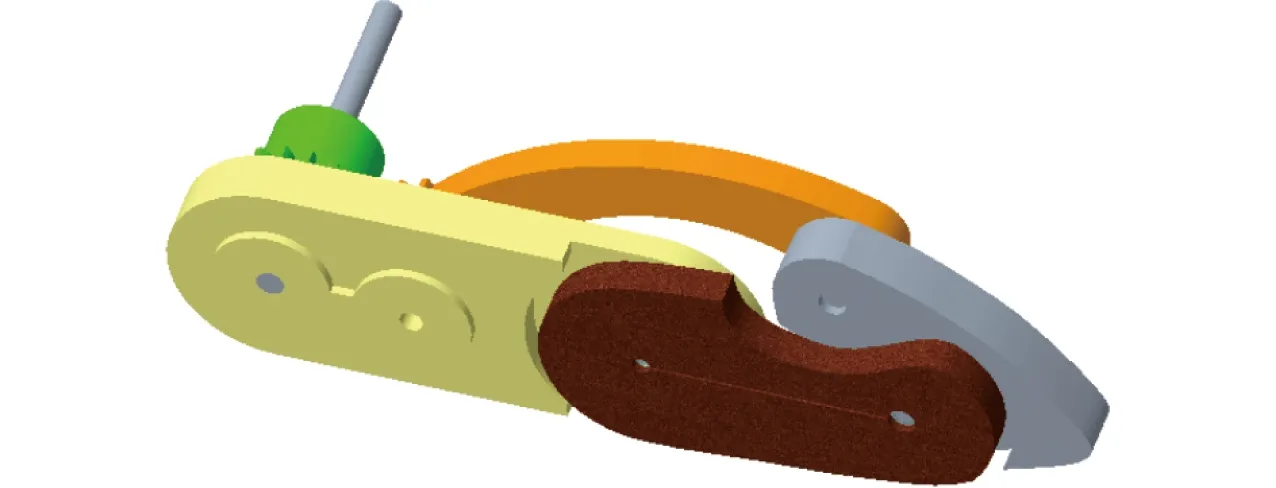
圖13 新型手指機(jī)構(gòu)的三維模型Fig.13 3D model of new finger mechanism

為了進(jìn)一步驗(yàn)證本文設(shè)計(jì)方法的正確性和可行性，通過(guò)光敏樹(shù)脂光固化成型工藝得到了手指機(jī)構(gòu)樣機(jī)并建立了試驗(yàn)平臺(tái)，然后在運(yùn)動(dòng)過(guò)程中采集手指機(jī)構(gòu)末端點(diǎn)運(yùn)動(dòng)過(guò)程的8個(gè)位置點(diǎn)的坐標(biāo)和角度(包括給定5位姿點(diǎn)處)。圖14為手指機(jī)構(gòu)在給定的5個(gè)位姿點(diǎn)處的狀態(tài)，表4為5位姿點(diǎn)處的平均誤差。

圖14 手指機(jī)構(gòu)的5位置及其軌跡Fig.14 Five position points and their trajectories of new finger mechanism

通過(guò)5次手指運(yùn)動(dòng)試驗(yàn)采集數(shù)據(jù)求取平均值得到具體數(shù)據(jù)，并以此數(shù)據(jù)采用Matlab進(jìn)行多項(xiàng)式擬合最終得到手指機(jī)構(gòu)的實(shí)際軌跡，如圖15所示。

試驗(yàn)結(jié)果表明，所設(shè)計(jì)的手指機(jī)構(gòu)可以很好地

表4 手指機(jī)構(gòu)的誤差Tab.4 Error of new finger mechanism

圖15 手指機(jī)構(gòu)的實(shí)際和理論軌跡對(duì)比Fig.15 Comparison of actual and theoretical trajectories of new finger mechanism

滿(mǎn)足三關(guān)節(jié)位姿約束要求，理論和實(shí)際末端運(yùn)動(dòng)曲線(xiàn)大致相同。其手指末端的最大位置誤差為1.1 mm，最大姿態(tài)誤差為1.2°，其主要由手指關(guān)節(jié)的制造、裝配誤差所引起。

5 結(jié)論

(1)通過(guò)運(yùn)動(dòng)學(xué)映射理論以及SVD分解方法求解了三關(guān)節(jié)約束的五桿機(jī)構(gòu)鉸鏈點(diǎn)A和B曲線(xiàn)，并結(jié)合非圓齒輪傳動(dòng)理論進(jìn)行了手指機(jī)構(gòu)運(yùn)動(dòng)綜合。根據(jù)手指樣機(jī)驗(yàn)證了該理論的正確性和可行性。

(2)建立了單驅(qū)動(dòng)非圓齒輪五桿手指機(jī)構(gòu)的IO方程，并通過(guò)Matlab程序求解出理論軌跡。樣機(jī)手指機(jī)構(gòu)的末端的最大位置誤差為1.1 mm，最大姿態(tài)誤差為1.2°，其理論和實(shí)際的末端運(yùn)動(dòng)曲線(xiàn)大致相同，驗(yàn)證了本文所提出的設(shè)計(jì)方法。

(3)所求解的鉸鏈點(diǎn)曲線(xiàn)能滿(mǎn)足所提出的三關(guān)節(jié)位姿約束要求，可根據(jù)實(shí)際仿生手指的設(shè)計(jì)目標(biāo)和用途，選取合適機(jī)構(gòu)參數(shù)，滿(mǎn)足不同設(shè)計(jì)要求并為進(jìn)一步的手指機(jī)構(gòu)結(jié)構(gòu)優(yōu)化提供基礎(chǔ)。