藥學類專業開設多變量解析課程的可行性研究

布 仁，蓮 花，蘇日娜，牧 丹，白文明

（內蒙古醫科大學藥學院，內蒙古 呼和浩特 010010）

隨著時代的發展、科技的進步，時代賦予醫藥工作者以更高的要求，醫藥工作者應以更快的速度提供更好的藥物，這就要求醫藥工作者必須有更為扎實的基礎知識、更加過硬的基本素養技能。藥學相關工作具有實踐性、技能性、綜合性等，該專業學生應具備扎實的藥學相關專業知識。醫藥學本科院校設置的藥學類專業包含藥學、藥物制劑、臨床藥學等多個專業[1]，其開設的核心課程有藥物制劑、藥理學、藥物化學、藥物分析、醫藥數理統計等課程。大四學年設置的畢業專題研究既是本科階段所學各類知識的綜合應用訓練，也是完成學校各項科研任務的重要支撐。藥學類專業涉及的畢業研究課題大多是以測量數據為基礎的實驗研究，隨著現代儀器測試技術的飛速發展，采集數據的分辨率、維度及范圍都得到了提高和擴展，即數據變量增多、數據量發生爆炸式增大，所以如何對多變量大數據進行處理和分析已成為實驗研究面臨的重要課題。但是，現階段國內各院校設置的藥學類專業并未開設專門面向實驗測試數據解析的獨立課程，數據解析方法的學習更多依靠自學。如前所述，隨著實驗數據量和數據結構的變化，簡單的數據處理方法有時無法達到數據解析的目的，有效的數據解析常需要結合復雜的數學算法、統計學原理及計算機技術，所以數據解析技能的培養不能僅僅依靠學生的自學，非常有必要開設專門課程，系統、全面地學習相關算法、原理及數據解析特點等。

多變量解析是指對多變量數據進行數學、統計學分析的方法總稱。多變量數據解析方法種類繁多，根據分析對象數據的類型（形式）和分析目的等，解析方法也不盡相同。選擇合適的數據解析方法，正確完成數據分析是確保課題研究順利進行的重要前提。本文結合授課群體的專業特點、實際需求及數據解析目的，研究討論了藥學類專業開設多變量解析課程的可行性，為多變量解析課程的開設提供理論依據及參考。

1 實驗數據解析的必要性

實驗研究的分析對象多為復雜體系，現代分析測試技術通過增加數據采集點、通道數及維度等方式顯著提高了采集數據對目標屬性的解釋能力，即增加了實驗數據包含的有效信息。與此同時，實驗數據的結構變得更加復雜，數據解析的難度隨之增大。現階段，藥學類專業開設的數據解析相關的課程有高等數學、線性代數及統計學等，但都側重于數學原理的講授，缺乏對實際實驗數據的解析案例，學生雖然掌握了一些數學基礎知識，但是遇到解析具體實驗數據時，往往會出現無從下手的狀況。實驗數據解析，究其本質是尋找自變量與因變量之間相關關系的過程。通過實驗獲得的結果，從理論上都可以歸屬為自變量，可以是數值變量，也可以是分類變量[2]。而因變量是由自變量的變動引起的結果，在課題研究中因變量往往被設定為與研究目的直接相關聯的具體變量，與自變量相同，類型有數值變量和分類變量兩種。實驗數據中不僅包含與目標屬性相關的有效信息，同時還含有大量無效信息，如由于儀器噪音、測量條件的變化引起的背景干擾、與目標屬性無關的共存物質的響應及樣品物理化學狀態的差異引起的干擾響應等。由于數據采集過程中無法對上述類型的無效信息進行過濾，所以由各類測試技術采集得到的是同時包含了有效信息和無效信息的混合數據。在實驗研究過程中，有效地分離數據包含的無效信息和有效信息、降低無效信息的干擾及消除變量間的共線性等問題是現代科學研究共同面臨的課題。將數學和統計學的方法應用于實驗數據的解析過程，即多變量解析，是解決實驗研究中各種問題的有效手段。

醫藥學高等院校作為培養醫藥專業人才的陣地，本科階段的課程體系應根據專業發展的新特點和新需求進行合理調整，以求培養出適應新時代要求的合格專業人才。所以，在藥學類專業的課程體系中增設多變量解析課程完全符合專業發展的特點和需求，對提高人才層次、社會適應度及專業技能等方面有重要的現實意義。

2 多變量解析課程的授課特點

探究實驗結果與影響實驗結果的因素之間的關系是實驗研究的最終目的。作為解析手段，我們可以逐一討論各個因素（變量）與結果之間的關系，這種手法被稱為單變量解析。當然，單一的因素可能無法充分解釋結果，所以必須把所有因素都考慮進去，用這些因素綜合解釋結果。但是，往往各個因素之間又存在一定的相關，關系會變得非常復雜。因此，對各個因素進行逐一討論后，綜合解析的手法不僅費時費力，且當因素數目增多時，這種綜合解析本身就變得非常困難。所以需要一種能夠將相互關聯的因素（即實驗數據）所具有的特征進行匯總，并根據目的進行合成的技術，該技術稱之為多變量解析。隨著計算機的普及和軟件技術的迅速發展，多變量解析法在包括自然科學和人文科學在內的各個領域得到了廣泛應用。作為以實驗研究為主體的相關工作人員而言，掌握多變量解析方法是必備的實踐技能之一。根據現有理論統計，多變量解析方法有上百種，想要對所有內容進行充分理解，必須具備非常高階的數學知識。而對于除少數統計學專家之外的大部分人而言，只要具備清楚理解多變量解析的目的，在可能的范圍之內掌握幾種具有代表性的解析方法，對解析結果進行正確解釋的能力即可。

如前所述，多變量解析法的種類繁多，如果不對其進行歸類區分的話，很容易帶來混淆概念，混用亂用的現象。根據各類解析手法的特點總結出的分類結果[2]見圖1。

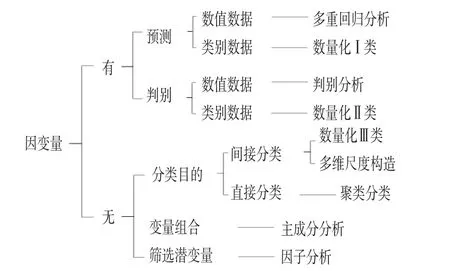
圖1 多變量解析手法的分類樹形圖

3 課程內容的選擇

如前所述，多變量解析方法種類繁多，將所有解析方法全部進行講解對于單一的一門課程而言，任務過重，負擔太大，幾乎不可能完成。根據數據結構特點和解析目的不同，多變量解析方法在不同領域中的具體應用存在很大差異。筆者試圖從藥學類專業的學科特點出發，從眾多解析法中精煉出部分具有代表性的多變量解析方法，通過對其方法內容、目的、適用范圍及結果解釋邏輯等進行講解，使學生系統地掌握常用的多變量解析方法，并能自主地將所學方法適用于多變量數據的解析。

藥學類專業常用的多變量解析法有聚類分析、主成分分析（PCA）、因子分析、多元回歸分析、判別分析、K近鄰分析、數量化分析、主成分回歸分析、偏最小二乘（PLS）回歸分析等。該課程將以定性分析和定量分析領域常用的聚類分析、主成分分析、PLS回歸分析為主線，對多變量解析法進行講解。

3.1 聚類分析

聚類分析是指在對已知樣品和未知樣品不進行區分的前提下，利用n維坐標（每個樣品有n個測量值）內的所有樣品間的歐幾里得距離的長短對樣品進行分組的方法[3]。該方法可以得出已知樣品的分散程度、未知樣品在各個已知樣品組的歸屬和未知樣品在所歸屬的已知樣品組內與哪個已知樣品最相似等信息，且當未知樣品不歸屬任何已知樣品組時，仍可以將這種無歸屬的情況進行明確的判別。

在進行聚類分析前可以通過PCA對所有用于聚類的樣品進行奇異值分析，進而去除奇異樣品。為了讓聚類分析的結果易于理解，利用樹狀圖表示樣品間的關系。樹狀圖的橫軸表示的是由歐幾里得距離確定的相似度，縱軸為樣品編號。

3.2 主成分分析

主成分分析是指在盡量不丟失原有信息的前提下，將已知樣品和未知樣品的測量值構成的矩陣進行降維的方法[4]。該方法由一系列步驟構成，首先是將所有樣品按測量項目進行排列，得到行數等于樣品數、列數等于測量項目數的矩陣數據。其次，將上述矩陣投影到與測量項目數相等的多維坐標系中（一個點即一個樣品），并且按照最大限度提取所有樣品各個測量項目反映的共同信息的方式繪制新坐標軸，該坐標軸稱之為第一主成分。而第一主成分無法全部描述所有的原有信息，所以用相同的方法對剩余信息繪制第二條坐標軸，稱之為第二主成分，且該坐標軸應正交于第一主成分，即第二主成分反映的信息與第一主成分反映的信息間完全不相關。依上述方法還可以得到更多的主成分，直至原有的信息全部被提取出來為止。在主成分分析中，將樣品在上述新的坐標軸即主成分上的投影稱之為該樣品在該主成分上的得點（score）。

在定性分析過程中，以主成分為坐標軸，基于主成分得點用二維或三維圖表示樣品分布狀況的做法即為主成分分析法。另外，還可以通過對主成分得點和樣品含量數據進行多元回歸的方式進行定量分析，該方法稱之為主成分回歸分析法。

3.3 PLS回歸分析

基于多元回歸的定量分析受到自變量間存在的多重共線性的影響，其預測精度將大大降低。主成分回歸分析雖然解決了自變量間存在的多重共線性問題，但是主成分提取過程中未考慮自變量與因變量間的關系，所以回歸精度仍然可能不足。為了提高回歸分析的預測精度，提出了PLS回歸分析[5]。對實驗數據進行PLS回歸分析時，首先需要在保證潛變量與因變量間的協方差最大，且潛變量間完全不相關的條件下提取潛變量。再基于部分潛變量和因變量進行多元回歸分析，即得到預測因變量數據的數學模型。當然，建立定量預測模型的過程當中還必須考慮構造模型的潛變量數、有效變量的選擇及模型的評價等相關問題，一并將在課程內容當中予以體現。

本課程內容除了上述3種多變量解析方法外，還將包含與這三類方法相似、相關的其他多變量解析內容。例如，與聚類分析法相關的判別分析、數值化分析，與主成分分析法相關的因子分析、獨立成分分析，與PLS分析相關的PLS-DA分析、正交PLS分析等方法[6-9]都將是本課程的講授內容。

4 結語

隨著計算機和各種統計軟件的普及，多變量解析法已然成為實驗研究數據分析不可或缺的重要工具。但是，大部分相關人員未上過系統的多變量解析課程，對解析法的理解不全面，常出現解析法的不當應用等情況。常出現的不當應用有模型的不適用、有效變量的選擇錯誤、研究目的和解析方法不匹配、統計鑒定的混用和亂用等。所以作為培養專業人才基地的高等院校，應根據自身專業的學科特點開設多變量解析相關的課程，以培養出符合時代發展要求，具有合格的數據處理、分析能力的人才。