中間支撐剛度對雙跨梁屈曲穩定性的影響

毛曉曄， 邵志華， 舒 送， 范 鑫,3， 丁 虎， 陳立群

(1.上海大學 力學與工程科學學院 上海市應用數學和力學研究所，上海 200444；2.中國人民解放軍第5720工廠，安徽 蕪湖 241007；3.中國科學技術大學 精密機械與精密儀器系，合肥 230026)

管路系統是保障飛機飛行安全的最重要系統之一，其振動問題在使役過程中十分突出。飛機管路系統經常發生各種類型的故障，主要表現為管路系統振動故障，影響飛行安全，造成嚴重損失[1-2]。Gao等[3]綜述了2020年以前關于飛機管道故障以及減振的相關研究進展：根據美國統計，燃油、空氣和液壓管路系統的故障占飛機部件故障總數的50%～60%；據俄羅斯統計，燃油、潤滑油和液壓系統故障也占飛機故障總數的50%以上；近年來，我國飛機液壓管路系統也發生了多起振動故障，這些問題一直困擾著飛機設計者。

關于飛機液壓管路建模方法已有大批學者展開了廣泛研究，常見的管道模型大致分為三種[4]，分別是Euler-Bernoulli模型[5]，Timoshenko模型[6-7]以及殼模型[8-9]。基于這些模型，可以研究管道的受迫激勵[10-11]，參激共振[12-13]等動力學響應問題。這些管道模型理論研究表明：對于短粗管道，必須使用Timoshenko模型描述管道動力學；對于大管徑薄壁管道，則必須使用殼模型；而對于長徑比較大的細長管道，則一般使用Euler-Bernoulli模型進行分析。不管哪種模型，在軸向流速達到臨界值后，管道的直線平衡位形會失穩發生分岔現象[14-15]。在屈曲狀態下，管道會變為本質非線性，并且會產生雙穩態勢阱間跳躍的劇烈振動[16-17]。而這種流速改變結構本征特性的現象已經被美國航空航天局NASA實驗驗證[18]。工程中，除了流速會引起管道屈曲，管道上存在的壓力也會改變結構本征特性。例如環境溫度升高造成管道熱膨脹而產生軸向壓力，安裝操作中施加的旋緊壓力以及管道尺寸偏差帶來的壓力等，這些壓力都可能導致管道產生屈曲，因此對于管道的壓力不容忽視。

以上研究都是基于單跨管道進行的，在很多實際工況下，較長的管道需要在中部安裝卡箍或夾具，這些往往都是彈性約束，建模時可以簡化成具有一定剛度的彈簧[19-21]。例如，Gao等[22]提出了一種針對飛機長距離多支承液壓管路振動分析的模型, 通過引入人工彈簧模擬邊界條件，提出了一種有效的管道模型簡化求解方法，而且研究結果表明，該方法能夠顯著降低計算成本，且具有足夠的計算精度；而趙小穎等[23]在建模時直接將彈性支承力用Delta函數表示在結構控制方程中。不過，他們對于多跨結構的屈曲以及屈曲穩定性并未討論。

本文僅考慮壓力對管道屈曲的影響，并且低速流體對結構本征特性的影響并不顯著，因此建模過程中暫時忽略流體作用，將管道簡化為帶中間彈性約束的梁模型。以分段以及整體兩種方式，建立結構橫向振動控制方程。通過對比兩種模型，證實整體梁模型的精確性。在此基礎上進一步分析了雙跨梁的靜力學屈曲分岔現象，并得到了彈性約束對結構屈曲臨界狀態的影響作用。

1 數學模型

對于雙跨梁，有兩種建模方式。由于梁是一個連續體，可以將中間支撐所帶來的約束力作為梁上的集中力考慮；同時，也可以將梁分為兩段考慮，將中間支撐約束作為邊界考慮。第一種方法所建立的模型簡潔，用集中力表達支撐約束；第二種方法所建立的模型精細，用邊界連續性條件表達梁的整體性。考慮到計算簡潔，本工作將使用第一種模型進行分析計算，用第二種模型驗證第一種模型的精確性。

1.1 整體梁建模

整體梁分析模型，如圖1所示。靜態梁兩端鉸支點的距離為L，中間位置有一剛度為k的彈性支撐。梁的材料密度為ρ，橫截面積為A，楊氏模量為E，橫截面關于中性層的截面慣性矩記為I。梁受到軸向壓力P，建立該梁的面內振動模型，令梁上任意處的橫向位移記為w(x,t)，軸向位移記為u(x,t)。

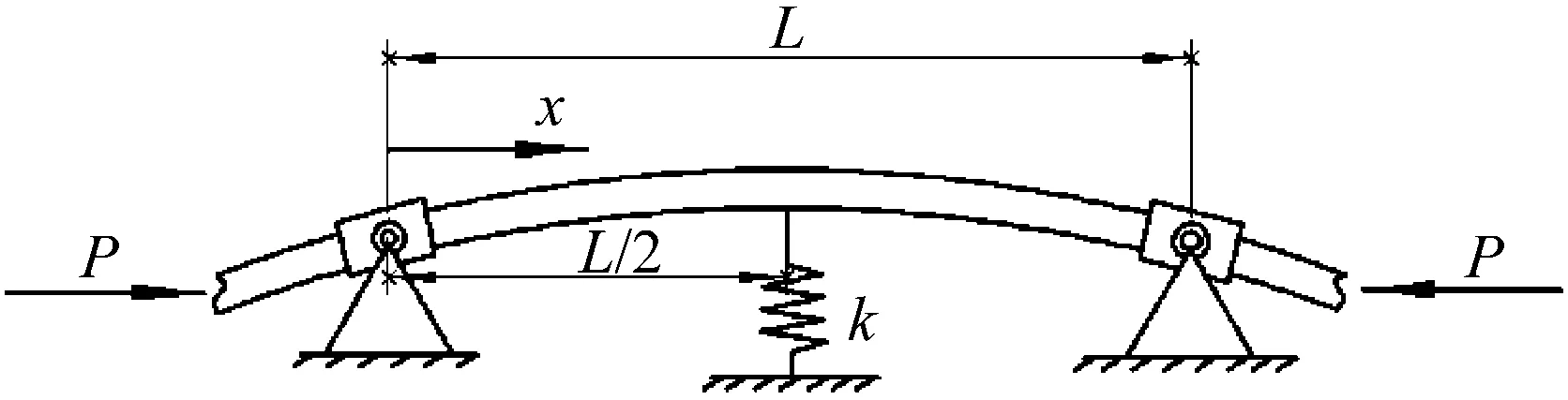
圖1 整體梁分析模型示意圖Fig.1 Schematic diagram of the continuous beam model

根據能量法建立運動方程。其中，T為梁的動能，U1為梁的勢能，U2為中間支撐彈簧勢能。則系統動能、勢能積分表達式分別為

(1)

式中：δ表示狄拉克函數；下標中量符號之前的逗號表示該量符號的偏導數；動能表達式包含梁縱向運動和橫向運動的動能。梁的勢能U1中，第一項是由中性面拉伸產生的勢能，第二項是彎曲所產生的勢能，第三項是與軸向壓力P有關的拉壓勢能。

將式(1)代入Hamilton變分原理

(2)

式中,ζ表示指定時間間隔內的變化量。

結合縱向位移遠小于橫向位移，可降維得到考慮幾何非線性的梁的積分-偏微分控制方程

(3)

以及對應的邊界條件

w(0,t)=w(L,t)=0,

w,xx(0,t)=w,xx(L,t)=0

(4)

忽略非線性項可得派生系統為

(5)

由于該模型受簡支邊界條件約束，可以假設上述方程的解為

(6)

代入控制方程得到

(7)

記式(7)等號左邊為Gn(x,t)，則n階Galerkin截斷可寫為

(8)

以此得到n個含有未知數qi(t)的常微分方程組，再令其中

qi(t)=Qieiωt，i=1,2,…,n

(9)

化簡后可得到方程組矩陣為

(H+K)Q=0

(10)

式中：H表示n階對角矩陣；K為n階剛度矩陣；Q為n階列向量。

(11)

(12)

(13)

(14)

若使式(10)有非零解，則系數矩陣H+K行列式值必然等于0。代入模型參數，對于給定的軸向壓力P和約束剛度k，即可得到相對應的頻率ω。

1.2 分段梁建模

雙跨耦合模型，如圖2所示。

圖2 雙跨耦合模型示意圖Fig.2 Schematic diagram of the double-span beam model

考慮到雙跨梁為對稱結構，可選取一側用能量法進行建模。一邊鉸支、一邊彈性約束的復雜邊界梁對應的動能、勢能為

(15)

根據Hamilton變分原理得到的復雜邊界約束梁的控制方程為

(16)

忽略其中的非線性項，得到派生方程

ρAwn,tt+EIwn,xxxx+Pwn,xx=0,n=1,2

(17)

記左邊梁為1，右邊梁為2，則w1表示1梁的橫向位移，w2表示2梁的橫向位移，兩者控制方程相同。

兩段梁對應的邊界條件和耦合連續條件為

w1,xx(0,t)=0,w1(0,t)=0,

(18)

通過分離變量法，設控制方程的解為

wn(x,t)=φn(x)eiωt,n=1,2

(19)

將其代入控制方程得到

EIφn(x),xxxx-ρAω2φn(x)+Pφn(x),xx=0

n=1,2

(20)

設上述4階常微分方程的解為

φn(x)=Aneλ1x+Bneλ2x+Cneλ3x+Dneλ4x

n=1,2

(21)

其中參數λ1,2,3,4為

(22)

將控制方程的解代入邊界條件和連續條件，可以化簡得到

MNT=0

(23)

式中:M為8階系數矩陣;N為8階列向量。

N=[A1B1C1D1A2B2C2D2]

(24)

其中

(25)

若方程有非零解則需要使系數矩陣M行列式為0，由此得到關于剛度k，壓力P以及頻率ω的關系式。給定中間約束剛度k，便可得到固有頻率ω隨軸向壓力的變化。

3 模型驗證

由式(18)可見，分段梁模型在中間支撐處可以嚴格表達剪力的突變，因此該模型精度更高。不過，該模型涉及到非齊次邊值問題，動力學響應求解復雜。而整體梁模型雖然不能嚴格表達中間支撐處的剪力突變，但是合理的截斷階數將會使該模型足夠接近真實條件。這里將從固有頻率的角度，對整體梁模型進行驗證，模型參數如表1所示。

表1 模型材料尺寸參數Tab.1 Parameters of the beam

整體梁在計算固有頻率時采用了Galerkin截斷，首先有必要討論其自身截斷收斂性，再將收斂的結果與分段梁得到的結果進行對比驗證。圖3展示了4階和6階截斷條件下，不同中間支撐剛度所對應的固有頻率隨軸力的變化，可見在所關注剛度范圍內，4階截斷已經具備較高的收斂性。

圖3 整體梁模型的截斷收斂性Fig.3 The truncation convergence of the continuous beam model

在整體梁自身截斷收斂性得到驗證后，圖4(a)～(d)對比分段梁模型和4階截斷整體梁模型所得到的不同剛度條件下，前4階固有頻率與軸力之間的關系。觀察到雖然兩種建模方式不同，但是兩種模型得到的頻率幾乎完全擬合，這說明收斂的整體梁模型具有合理的精度表達中間支撐剛度所引起的梁固有特性的改變。

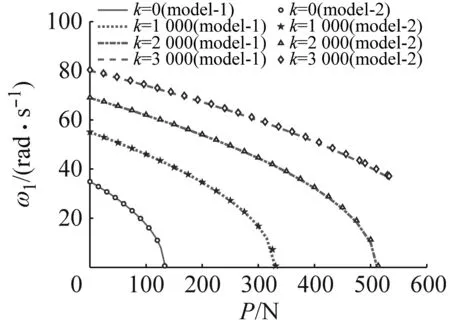
(a) ω1隨軸力的變化

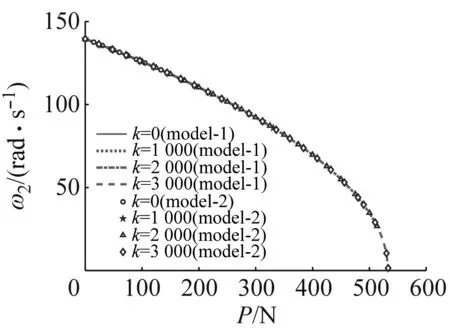
(b) ω2隨軸力的變化

(c) ω3隨軸力的變化

(d) ω4隨軸力的變化

(e) Pcr隨支撐剛度的變化圖4 兩種梁模型的對比驗證Fig.4 Comparison and verification of the two beam models

當軸力足夠大時，固有頻率會變為0，此時發生屈曲失穩。圖4(e)則對比了兩種模型分析得到的臨界軸力，可見中間約束剛度的增加首先會提高臨界狀態對應的屈曲力，但是當剛度達到一定大小以后，這種對臨界軸力的放大作用消失，最終收斂于半長簡支梁的臨界屈曲壓力。

由于已經驗證了4階截斷整體梁模型的收斂性和精度，可以在4階截斷基礎上推導出一階屈曲軸力為

(26)

當彈簧約束剛度為0時，可退化得到壓桿的Euler定理Pcr=π2EI/L2；而當約束剛度足夠大時，一階臨界壓力為Pcr=4π2EI/L2。

2 屈曲位形

如果梁所受軸向壓力超過臨界屈曲值，就會發生屈曲失穩，表現為直線平衡位形失去穩定，固有頻率變為0。在非線性項的作用下，梁會出現曲線平衡位形，也叫非平凡靜平衡位形。第1章已經驗證了整體梁模型的精確性，由于計算簡潔，本章將以該模型為基礎，計算不同中間支撐剛度下，雙跨梁的屈曲位形變化。

由于位形函數只與空間坐標有關，因此忽略控制方程中顯含時間的項與激振力項，整理可得位形滿足的方程為

(27)

以及對應的邊值條件

(28)

(29)

分別取n=4，6進行截斷，將式(29)代入式(27)中，方程兩端同時乘以權函數sin(jπx/L)，并對x進行從0～L的積分，得到關于系數Bk(k=1…n)的n階方程組。為了便于不同剛度下的對比，選取軸向力P=101%Pcr，剛度和對應壓力值的選取參數如表2所示，模型其他參數值見表1。

表2 模型彈性支承剛度和對應的壓力值Tab.2 The bearing stiffness and the pressure

聯立n個截斷方程，計算參數B1～Bn的取值，便可得到不同剛度、不同截斷階數所對應的屈曲位形系數。

2.1 截斷收斂性隨支撐剛度的變化

第一章已經通過對比驗證得到，在自身收斂的條件下，整體梁模型可以擁有合理的精度近似描述中間支撐剛度引起的剪力突變。因此，在計算屈曲位形時，依然必須對截斷的收斂性進行判定。然而，由于式(27)中非線性項的存在，過大的收斂階數下，軟件直接計算位形系數會變得非常困難。不過，考慮到屈曲位形的解必然存在，高階截斷也僅僅是對低階截斷的修正，于是考慮利用4階截斷的位形系數作為迭代初值，使用牛頓迭代法，進行高階截斷位形系數的計算。

記截斷后得到的n個關于位形系數B=(B1,B2,…,Bn)T的多元非線性代數方程為F=(f1,f2,…,fn)T，寫為矩陣形式

F(B)=0

(30)

代入牛頓迭代公式，則有

B(k+1)=B(k)-J[F(B(k))]-1F(B(k)),

k=1,2,…,n

(31)

其中J[F(B(k))]-1是式(30)的Jacobian矩陣的逆矩陣，記

(32)

當滿足ε<1×10-10時，輸出結果B，計算流程如圖5所示。

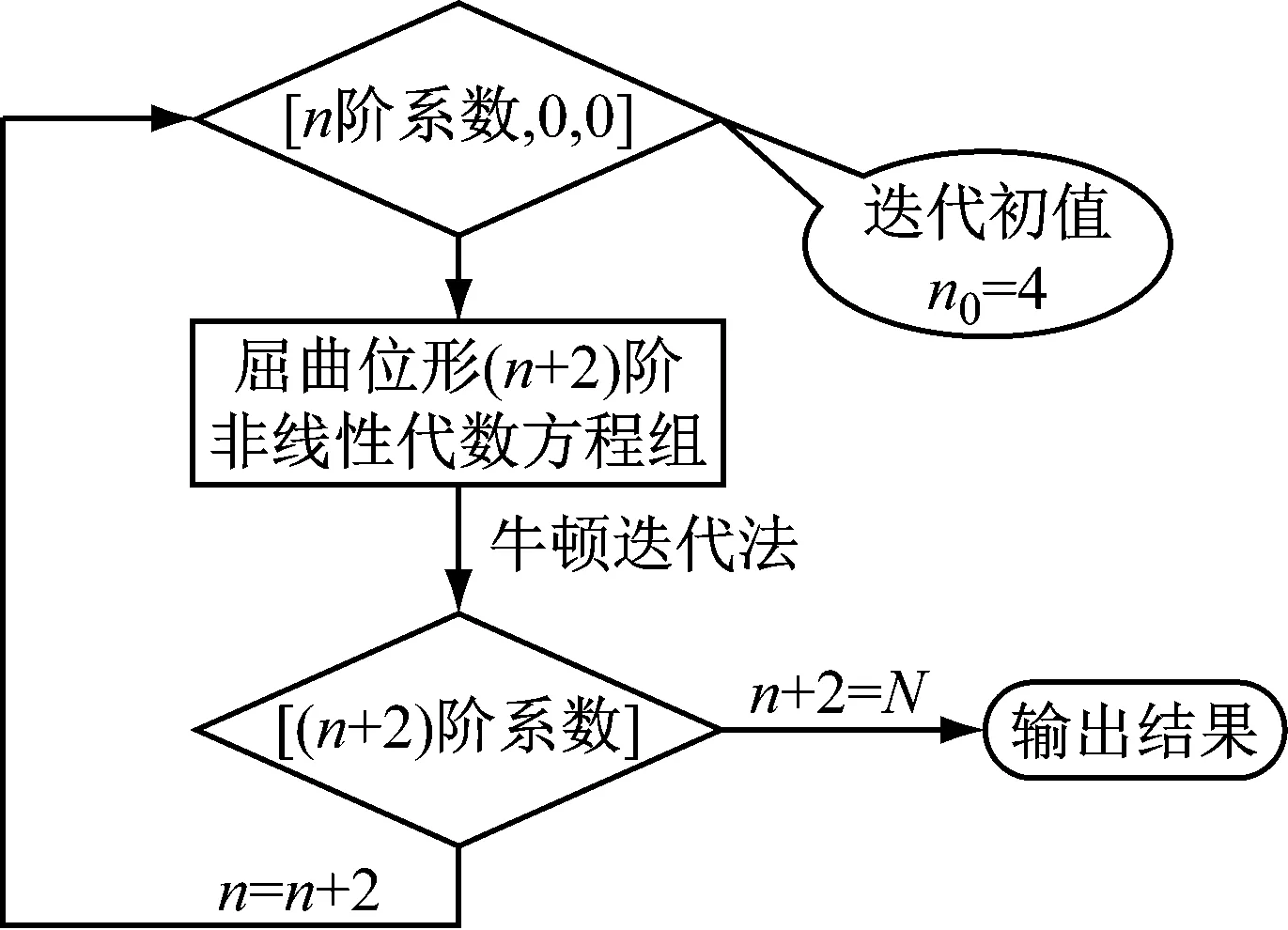
圖5 高階屈曲位形系數計算流程圖Fig.5 Flow chart for calculating higher order flexural configuration coefficients

從4階截斷求得的屈曲位形開始計算,系數如表3所示。可見對于一階屈曲位形，僅有奇數階模態上存在非0系數；而對于二階屈曲位形，僅二階模態上存在非0系數。4階截斷所得到的前兩階屈曲位形如圖6所示，每階屈曲位形都存在對稱的兩組解，為圖形清晰，后續屈曲位形圖形僅畫出其中一組結果。

(b) 第二階正負屈曲位形圖6 4階截斷處理不同剛度作用下前兩階臨界屈曲位形Fig.6 The first and the second order critical buckling configuration with different stiffness under the fourth order truncation treatment

表3 前兩階屈曲位形系數(截斷階數n=4)Tab.3 Coefficients of the first and the second order buckling configurations (truncation order n=4)

除4階截斷求得的一階正位形的位形系數B1～B4，其他系數初值均取0，以此作為初值。利用上述迭代方法，可以得到不同剛度、不同截斷階數下的位形系數，得到的位形曲線如圖7所示。可以看到，剛度k=1 000時，12階截斷可滿足其收斂性；剛度k=2 000時，16階截斷可滿足位形收斂性。可見，對于一階屈曲位形，約束剛度越大，對收斂階數的要求會越高。

(a) k=0

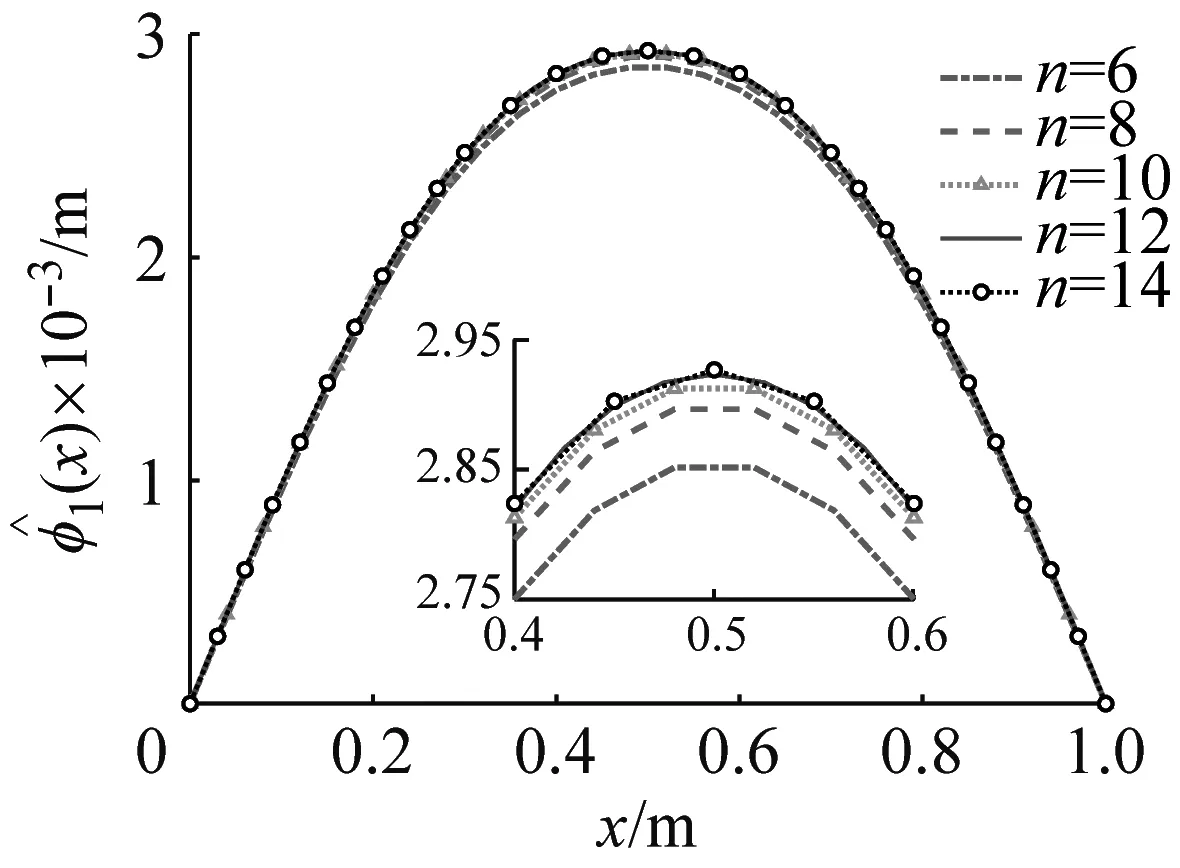
(b) k=1 000 N/m

(c) k=2 000 N/m圖7 不同截斷階數下第一階屈曲位形Fig.7 Comparison of the first order buckling configurations under different truncation orders

同樣，取4階截斷求得的二階位形系數中的一組作為初值，其他系數初值也依然設置為0，經迭代后，得到不同剛度系數、不同截斷階數下的二階位形系數，如圖8所示。顯然，二階屈曲位形上，截斷的收斂性不受中間剛度變化的影響。并且，即便使用更高的截斷階數，二階位形系數中也僅二階模態系數不為0，即二階屈曲位形僅需二階模態即可嚴格表達。

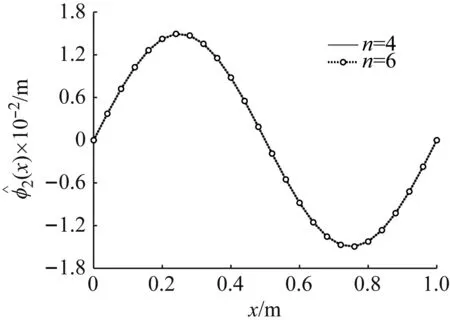
(a) k=0

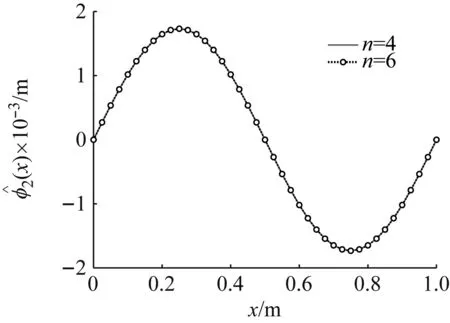
b) k=3 000 N/m圖8 不同截斷階數下第二階屈曲位形對比Fig.8 Comparison of the second order buckling configuration under different truncation orders

2.2 屈曲位形隨支撐剛度的變化

圖9將不同剛度下收斂的屈曲位形進行對比，可以看到，剛度對前兩階的屈曲位形影響都很大。隨著剛度增加，二階位形會受到彈性約束而減小，一階屈曲位形會變大。特別對于一階屈曲位形，隨著約束剛度的增加，原本只有一階系數項非0的屈曲位形，逐漸受到三階系數項的作用而遠離半周期正弦函數，而且剛度越大，這種改變越明顯。而剛度在達到3 000 N/m時，一階屈曲位形產生本質性改變，表現出反曲現象。這需要對位形的穩定性進行分析，以厘清這些復雜現象的真實性。

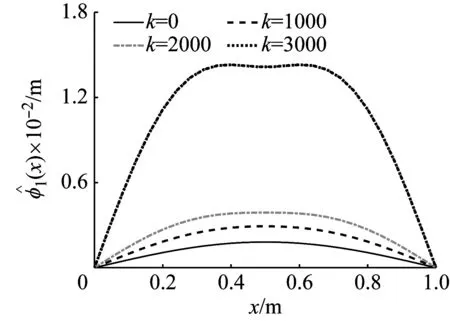
(a) 第一階正屈曲位形

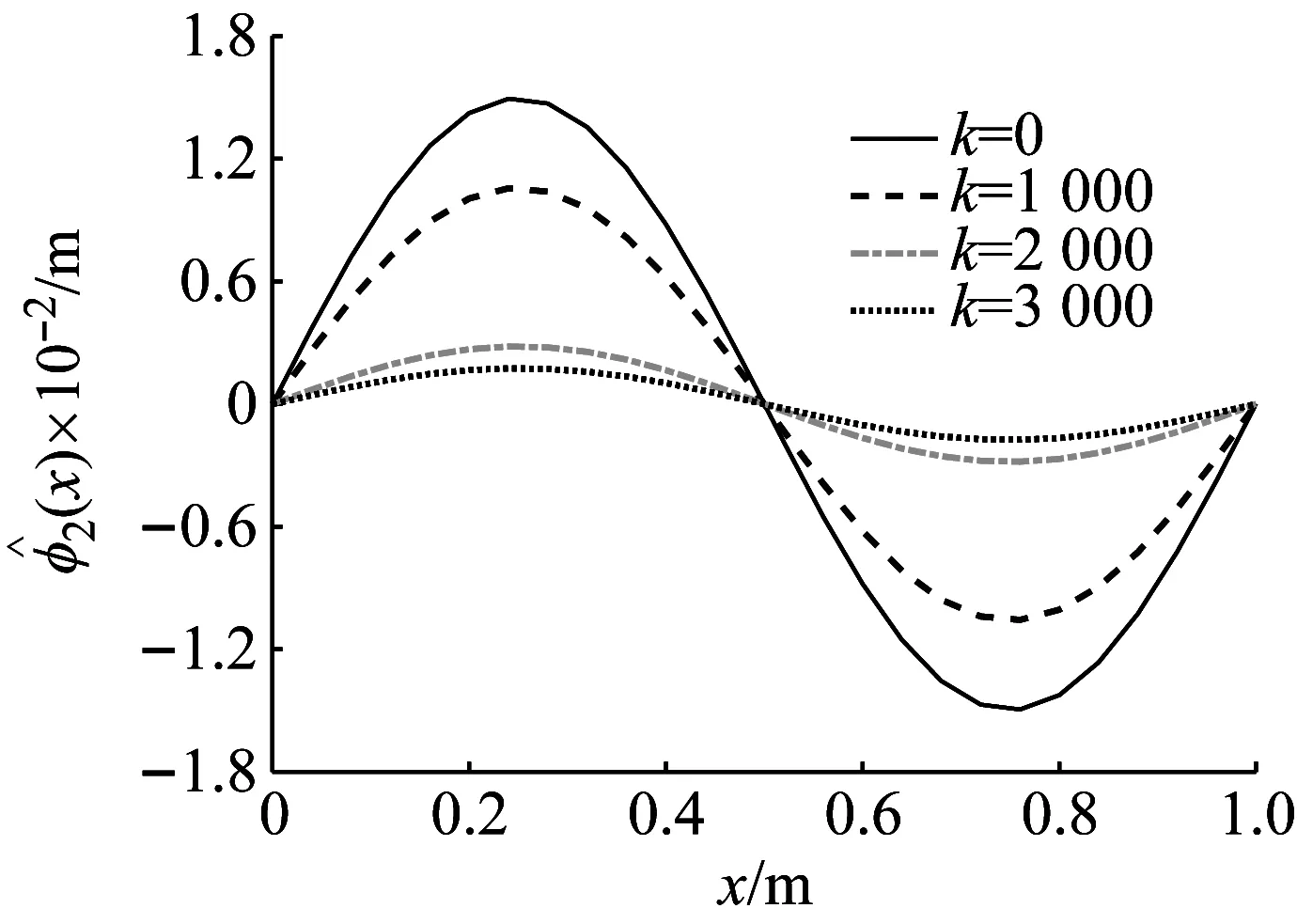
(b) 第二階正屈曲位形圖9 不同剛度作用下前兩階收斂屈曲位形對比Fig.9 Comparison of the first and second order convergent buckling configuration under different stiffness

3 位形穩定性分析

第二章對屈曲位形的計算中，不同支撐剛度條件下都會出現多組屈曲位形系數的實數解，不過它們并不一定都是穩定的，本章將對前兩階屈曲位形的穩定性進行討論。以收斂的截斷階數，計算屈曲位形穩定性隨中間支撐剛度的變化。

3.1 穩定性的數學判斷

為進一步研究屈曲穩態構型周圍的振動特性，首先作如下坐標變換

(33)

將式(33)代入控制方程(3)，并結合屈曲平衡方程(27)，得到關于v(x,t)的非平凡位形基礎上的振動控制方程

(34)

(35)

選取符合邊界條件的多自由度橫向位移表達式

(36)

將式(36)代入式(35)，兩端同乘以sin(jπx/L)并進行對應收斂階數的截斷，得到非平凡位形上的n階未擾系統方程組

(37)

將式(37)改寫為

(38)

其中

y=q

(39)

進而求得該系統的2n階Jocabian矩陣

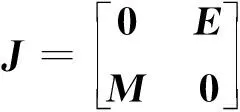
(40)

式中：E為n階單位矩陣；M為系數矩陣，是關于參數P，k，E，L，I，ρ以及B1～Bn的n階對稱矩陣。

根據λE-J得到矩陣J的特征方程，以及對應的平衡點系數，解出特征值λn。利用常微分方程平衡點穩定性知識可知，當該平衡點的一系列特征值中存在正實部時，平衡點不穩定。

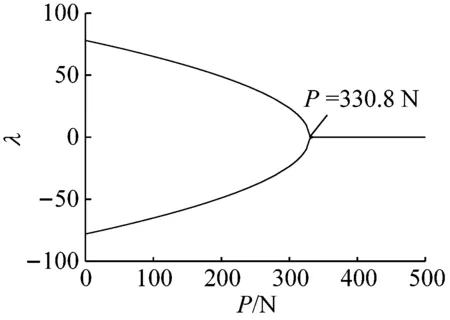
圖10、圖11以及圖12分別給出了中間支撐剛度為1 000 N/m、3 000 N/m以及100 000 N/m時平凡位形以及前兩階非平凡位形的特征值穩定性分析。從圖10可以看出，隨著軸力的增加，平凡位形在超過臨界軸力后失穩，而一階非平凡位形變得穩定；與此同時，二階非平凡位形特征值雖然會產生變化，但正實部一直存在，即在中間支撐剛度為1 000 N/m時，二階非平凡位形一直是不穩定的。

(a) 直線位形穩定性

(b) 一階非平凡位形穩定性

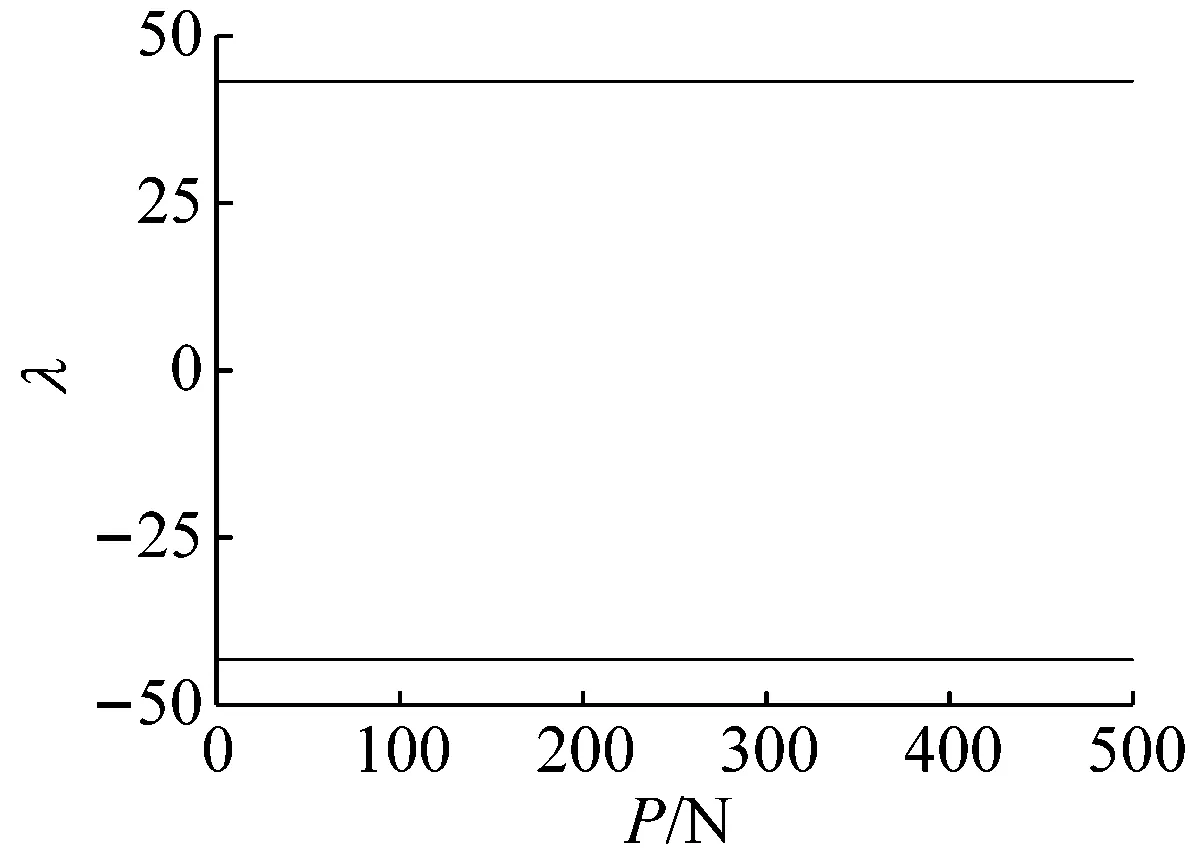
(c) 二階非平凡位形穩定性圖10 k=1 000 N/m時位形穩定性隨軸力的變化Fig.10 Stability of the configuration solutions changing with the axial force while the bearing stiffness is 1 000 N/m

(a) 直線位形穩定性

(b) 一階非平凡位形穩定性

(c) 二階非平凡位形穩定性圖11 k=3 000 N/m時位形穩定性隨軸力的變化Fig.11 Stability of the configuration solutions changing with the axial force while the bearing stiffness is 3 000 N/m

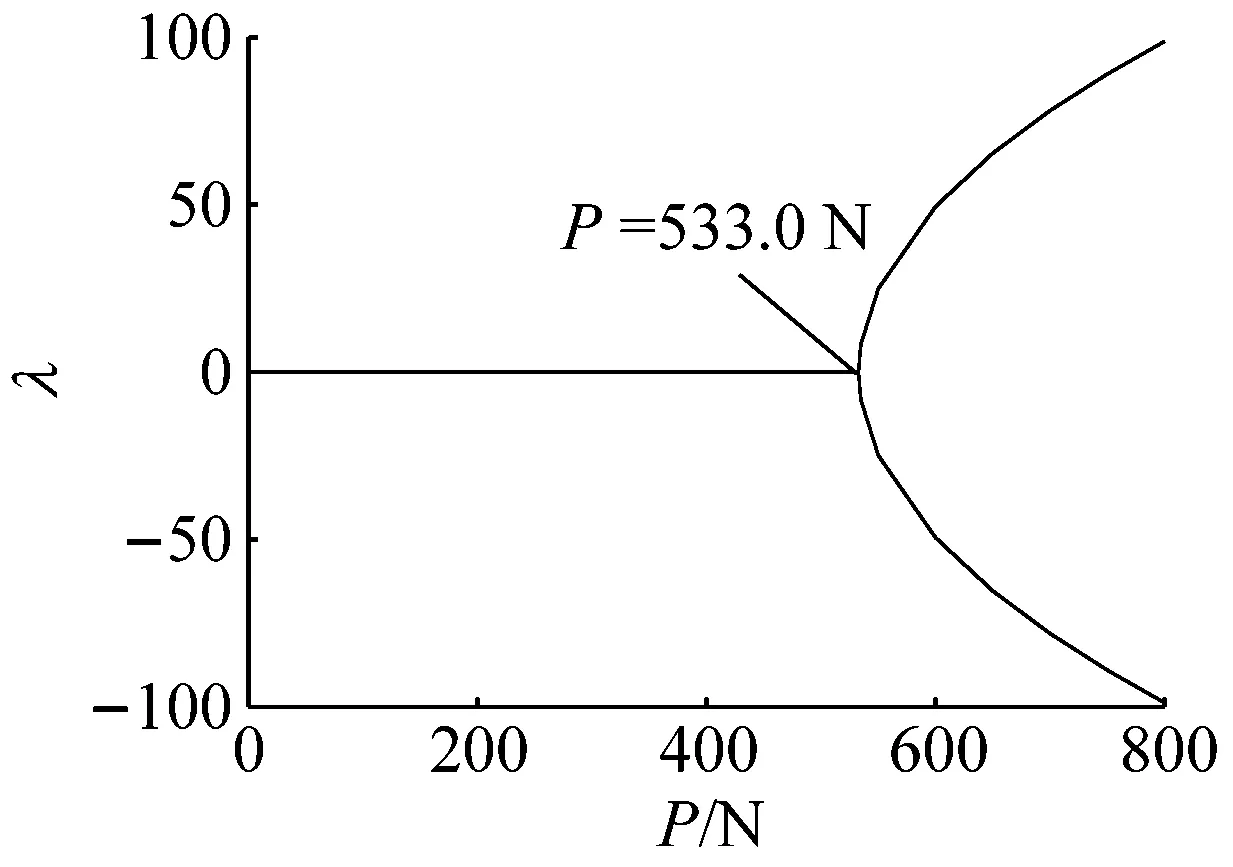
(a) 直線位形穩定性

(b) 一階非平凡位形穩定性

(c) 二階非平凡位形穩定性圖12 k=100 000 N/m時位形穩定性隨軸力的變化Fig.12 Stability of the configuration solutions changing with the axial force while the bearing stiffness is 100 000 N/m

從圖11可以看出，當中間支撐剛度較大時，平凡位形在超過臨界軸力后變得不穩定，而二階非平凡位形變得穩定。此時，雖然一階非平凡位形特征值產生變化，但是正實部一直存在，一階非平凡位形不穩定。

從圖12可以看出，當中間剛度近似于無窮大以后，位形的穩定性情況與剛度達到3 000 N/m時變化相同，屈曲以后從直線位形直接過渡到二階非平凡靜平衡位形達到穩定，說明此時穩定性不再隨剛度產生變化。

由以上對比可以得知，雖然非平凡位形有高階多解，但是給定軸向壓力和約束剛度下能夠滿足穩定的位形有且僅有只有一組(非平凡位形上下對稱，意義相同)。剛度較小時，壓力達到臨界值會由穩定的直線位形叉形分岔到穩定的一階非平凡位形。而在剛度較大時，臨界壓力作用下會使梁由直線位形直接分岔至穩

定的二階非平凡位形；而發生這一轉換的剛度臨界值即為式(26)推導得到的k=45EIπ4/28L3，代入參數后，此模型下的數值約是k=2 113 N/m。

3.2 一階非平凡位形穩定性的物理解釋

對于不同支撐剛度條件下，一階非平凡位形的穩定性可以從物理角度進行解釋。對一階非平凡位形函數求二階導，即可得到屈曲位形的曲率表達式。如圖13所示，剛度為0、1 000 N/m以及2 000 N/m時，其曲率在整個梁上任一點均是同號的。但是剛度達到3 000 N/m時，中間位置曲率出現異號。從不同支撐剛度下一階非平凡位形曲率的變化可以判斷，當中點處曲率等于0時，所對應的支撐剛度為臨界剛度。超過該剛度后，一階非平凡位形失穩，而平凡位形會直接分岔至二階非平凡位形。

圖13 不同剛度下一階非平凡位形的二階導數Fig.13 Second derivatives of the first-order nontrivial configurations with different bearing stiffness

4 結 論

以上工作通過兩種建模方式得到了帶中間彈性支撐的軸向受壓雙跨梁的運動控制方程，并在連續梁模型的基礎上，對中間支撐剛度的影響進行了詳細研究，得到以下結論：

(1) 連續梁模型的模態雖然處處連續可導，但經過足夠多的模態疊加，連續梁模型可以以合理的精度描述中間支撐處的剪力突變。

(2) 一階屈曲位形隨支撐剛度的增加遠離半周期正弦函數，并且需要使用更高階截斷才能使用連續梁模型得到收斂的屈曲位形。當中間支撐剛度超過臨界值后，一階屈曲位形失穩，物理表現為屈曲位形曲率出現異號。

(3) 二階屈曲位形截斷收斂性不受中間支撐剛度影響，僅使用單周期正弦函數即可精確描述二階屈曲位形。而當支撐剛度超過臨界值后，二階屈曲位形變得穩定，此時中間彈性支撐等同于節點。