一種異型沉箱浮游穩定性高效計算方法

馬 勇，方 波，譚彬政

（中交第四航務工程勘察設計院有限公司，廣東廣州 510290）

引言

國外某港口升級擴建項目，工程內容為新建一座15 萬t 級的現代化集裝箱碼頭和一座5 萬t 級的滾裝碼頭，碼頭結構采用傳統的重力式沉箱方案，標準沉箱為規則的矩形截面，但因在集裝箱碼頭與滾裝碼頭交接處，碼頭岸線存在約124°的夾角，為保證碼頭岸線的平順銜接，需在岸線相接位置設置一組橫截面不對稱的異型沉箱，其結構尺寸如圖1所示。

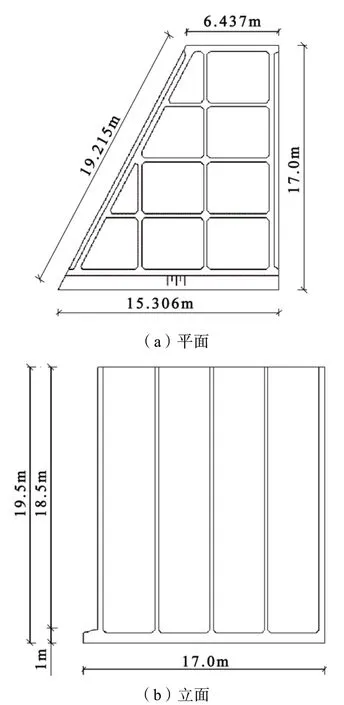
圖1 異型沉箱示意

對于橫截面不對稱的異型沉箱，若采用傳統的方法計算其浮游穩定性，計算過程繁瑣，且很難求解準確的計算結果[1]。為了解決這一難題，通過分析研究，提出了一套基于AutoCAD 和Excel 的高效求解方法，主要求解步驟如下：

1）基于材料力學的轉軸公式和慣性矩圓理論聯立求解得到不對稱截面的最小慣性矩及相應的形心軸；

2）利用AutoCAD 建模準確計算沉箱的幾何屬性；

3）根據沉箱浮游穩定的計算原理，結合已求得的沉箱幾何屬性，聯立相關數據的約束方程；

4）利用Excel 規劃求解功能求解上述約束方程；

5）求得各箱格內所需加注壓載水高度，即求解完成。

通過工程實踐驗證，該方法的理論計算結果與工程實際結果基本一致，有效解決了異型沉箱浮游穩定性計算的難題。

1 沉箱浮游穩定性的計算原理

在沉箱下潛、拖運、安裝過程中，為保證作業安全，需對沉箱的浮游穩定性進行驗算，并應滿足以下兩個條件[2-3]：

條件一：沉箱自身呈水平狀態，即沉箱頂面與水平面之間的夾角為0°，這要求沉箱的重心和浮心必須在同一條垂線上，重力和浮力對沉箱水平截面中的任一軸取矩均相等，滿足以下公式：

式中：

G為沉箱和壓載物的總自重（kN）；

a為重心到計算軸的水平距離（m）；

F為沉箱所受浮力（kN）；

b為浮心到計算軸的水平距離（m）。

通常情況下，沉箱在沒有壓載的情況，難以滿足上述條件，需通過壓載物將沉箱調平。

條件二：按照規范要求確定合適的沉箱定傾高度[4]：

1）對于短距離浮運工況（同一港區或30 n mile以內的運程），m≥0.2 m;

2）對于遠距離浮運工況（夜間航行或30 n mile以上的運程），固體物壓載，m≥0.3 m；液體壓載，m≥0.4 m。

定傾高度的計算公式如下[4]：

式中：

m為沉箱定傾高度（m）；

ρ為沉箱定傾半徑（m）；

a為沉箱重心到浮心的距離（m）。

沉箱定傾半徑按照如下公式計算[4]：

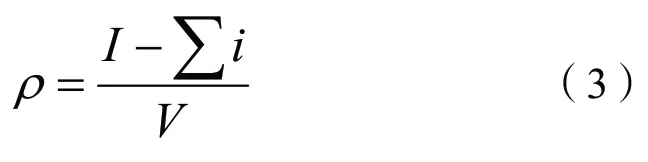
式中：

Ρ為沉箱定傾半徑（m）；

I為沉箱浸水面對應斷面對其截面形心軸的慣性矩（m4）；

i為第i箱格內壓載物的水平面對其指定截面形心軸（平行于沉箱的計算形心軸）的慣性矩（m4）。

V為沉箱的排水量（m3）。

由公式（1）、（2）和（3）可以看出，要計算沉箱的浮游穩定性，需要計算出沉箱的諸多幾何屬性參數，如沉箱的體積、重心、水平截面的面積及形心、各箱格的面積及形心，以及最小的定傾半徑等，其中，計算沉箱的最小定傾半徑，需找出沉箱浸水面對應斷面對其截面形心軸的最小慣性矩和對應的截面形心軸位置（即為沉箱浮游時的轉動軸），以及各箱格截面對其指定截面形心軸（平行于沉箱的計算形心軸）的慣性矩。

對于常規的矩形沉箱，上述各參數的計算較為簡單，簡單的手算即可得出，其水平截面最小慣性矩對應平行于長邊的形心軸。但是對于異型沉箱，若采用手算方法計算上述各參數，計算過程相當繁瑣，但采用AutoCAD 建立三維模型，則可方便快捷地解決該問題。

2 求解截面的最小慣性矩

2.1 轉軸公式

對于任意截面，當坐標系發生旋轉時，各坐標系下的截面慣性矩和慣性積之間存在一定的相關性，材料力學中稱之為轉軸公式[5]，具體如下：

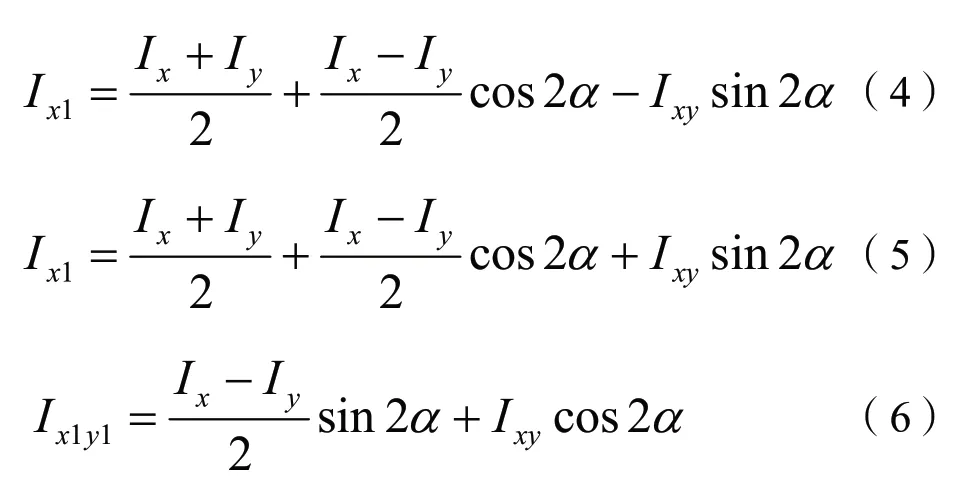
式中：

Ix、Iy、Ixy分別為對于截面內任意一個坐標系xOy，該截面對應坐標軸x，y的慣性矩和慣性積；

Ix1、I1y、Ix1y1分別為對于坐標系xOy 繞其原點O 逆時針旋轉α角得到的新坐標系x1Oy1，該截面對應新坐標軸x1，y1的慣性矩和慣性積。

2.2 慣性矩圓

聯立公式（4）、（6）及（5）、（6），可分別得到：

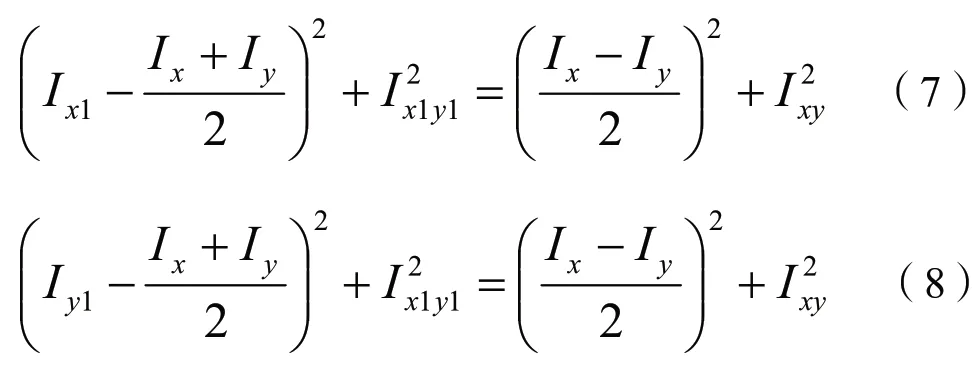
可以看出上式符合圓的解析表達式。對于截面內任一坐標系xOy，該截面對應坐標軸x，y的慣性矩和慣性積分別為Ix、Iy和Ixy，分別以慣性矩、對應的慣性積為橫、縱坐標，以（，0）為圓心、半徑，得到的圓形可稱為慣性矩圓，如圖2 所示。由公式(7)和(8)可知，慣性矩圓中任一直徑的兩個端點均對應一組在新坐標系（由原坐標系xOy 繞其原點O 旋轉所得）下的慣性矩和慣性積。

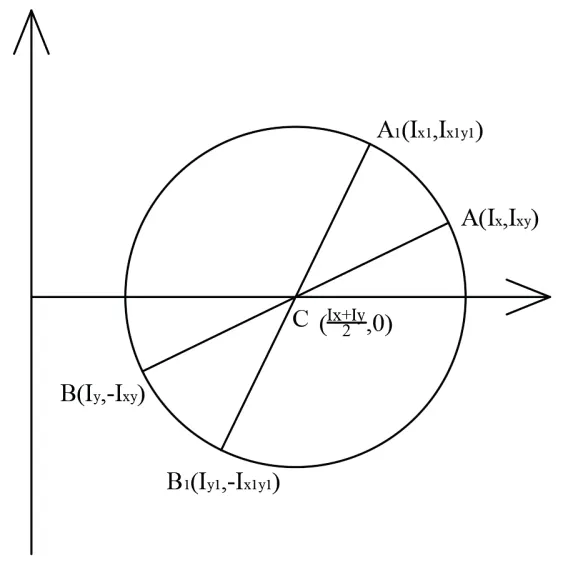
圖2 慣性矩圓

2.3 慣性矩和慣性積在慣性矩圓上的相互關系

在慣性矩圓中，假定已知坐標系xOy 下對應坐標軸x，y的慣性矩（Ix、Iy）和慣性積（Ixy）對應的直徑AB 與橫坐標軸之間的夾角為2α0，將直徑AB 逆時針旋轉2α角，可得一條新的直徑EF，其對應的端點坐標分別為點E（）、F，如圖3 所示。

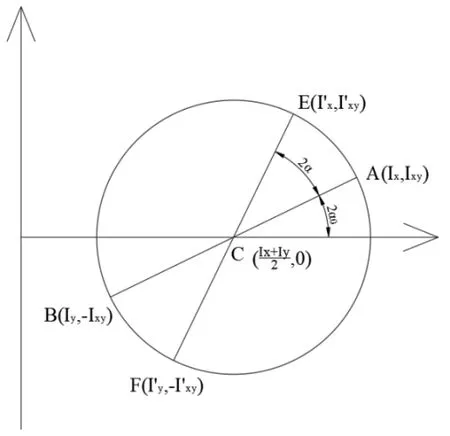
圖3 慣性矩圓中慣性矩（積）間的關系示意

根據圖3 得：

對比公式（4）、（5）和（6）可得：

根據上述分析可得，在慣性矩圓上，由已知坐標系xOy 下對應坐標軸x，y的慣性矩（Ix、Iy）和慣性積（Ixy）繪制一條直徑，將其繞慣性矩圓的圓心C 點逆時針旋轉角度2α，所得新直徑的兩個端點坐標即為截面對于原坐標系xOy 繞O 點逆時針旋轉α 角所得新坐標系x1Oy1的慣性矩和慣性積。

2.4 利用慣性矩圓求解截面最小慣性矩

觀察慣性矩圓可以看出，其水平直徑對應的慣性矩一個最小、一個最大。根據上一節的分析可知，此時對應的坐標系x’Oy’可由已知坐標系xOy 繞O點順時針旋轉角度a0得到，a0可由以下公式計算：

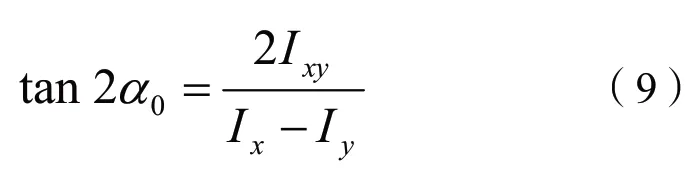
由此，可以得出對于截面內通過點O 的所有坐標系，截面在坐標系x’Oy’下的慣性矩和為大小極值，其數值可由以下公式求得：

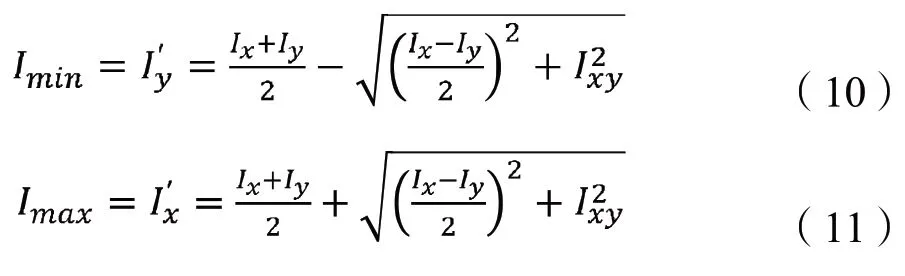
根據慣性矩的平行軸定理可知，對于截面內所有相互平行的坐標軸，截面對形心軸的慣性矩為最小。結合上述分析，如將坐標系xOy 的原點O 建立在截面形心上，則可通過公式(10)計算出截面的最小慣性矩。

2.5 非對稱截面沉箱浮游穩定的計算步驟

基于上述理論分析，下文將介紹依托項目中計算橫截面不對稱的異型沉箱浮游穩定的具體步驟。

1）繪制異型沉箱的水平截面A1（由外輪廓線生成），利用AutoCAD 中的查詢功能（命令Massprop）讀取截面A1 的形心，在截面A1 內以其為原點建立任意坐標系x0Oy0，如圖4，同時讀取截面A1 在坐標系x0Oy0下對應坐標軸x0和y0的慣性矩和慣性積、以及截面面積A[6]。

圖4 截面A1 內任意坐標系x0Oy0

2）利用公式（9）計算截面A1 的最小慣性矩所對應的坐標軸位置，由坐標系x0Oy0繞坐標原點O 順時針旋轉角度a0可得，從而建立新的坐標系xOy，如圖5 所示。

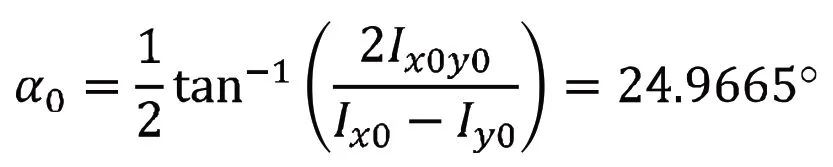
圖5 截面A1 的最小慣性矩對應的坐標系xOy

3）利用公式（10）計算截面A1 的最小慣性矩。

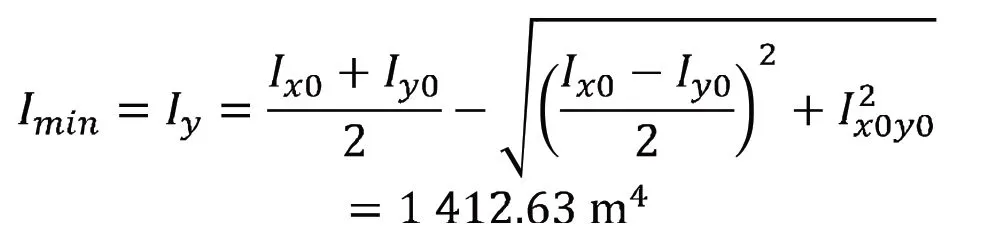
4）在截面 A1 中繪制各箱格的水平截面C1-C10，如圖6 所示。先在CAD 中讀取截面C1-C10 在新建坐標系xOy 下的形心位置（xi，yi）以及其對于y軸的慣性矩，然后利用平行軸公式求解各截面對于其自身平行于y軸的形心軸的慣性矩（Ii）。

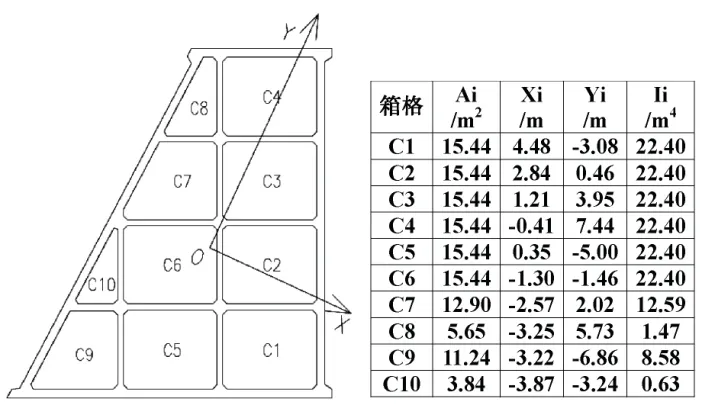
圖6 各箱格在坐標系xOy 中的位置及幾何參數

5）建立沉箱的三維模型[6]，在沉箱頂面以其截面形心為原點建立三維坐標系xyz，其中x軸和y軸的方向與第2 步中新建坐標系xOy 的坐標軸方向一致，z軸為沉箱高度方向，向上為正。在AutoCAD 中利用查詢功能（命令Massprop）可快速讀取沉箱的體積和重心位置等幾何屬性參數。

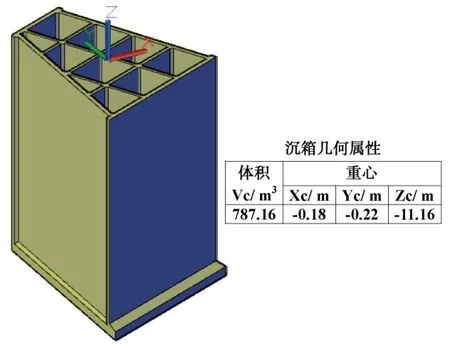
圖7 沉箱的三維模型及幾何屬性

6）假定各箱格內的壓載水高度為hi，采用Excel建立各數據間的相關性方程[7]，具體如下公式（12）～（16）。本文所研究的異型沉箱，扣除前趾和側趾，其在豎直方向上為等截面結構，因前趾和側趾的體積相對較小，其對浮心位置的影響可忽略不計，因此，可認為沉箱在水平狀態下的浮心在浸水面上的投影與浸水面的形心重合[8]，即在坐標系xyz中，浮心的x、y坐標值均為0。

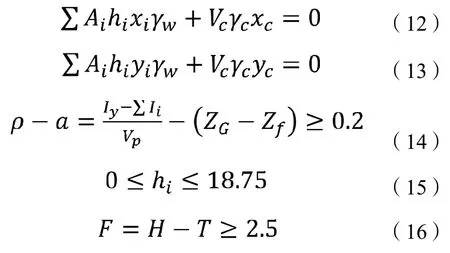
式中：

VP為沉箱加壓載水后的排水體積（m3），

ZG為沉箱加壓載水后，其重心在z軸上的坐標值，

Zf為沉箱加壓載水后，其浮心在z軸上的坐標值，

H為沉箱高度（m）；

T為沉箱加壓載水的吃水（m），

F為沉箱浮運時的干舷高度（m），對于本次計算的異型沉箱，依據規范[4]計算，干舷高度應不小于2.5 m。

對于沉箱內隔板，浮運期間的水頭差是其承受的主要荷載，因此在確定箱格內壓載水高度時需控制相鄰箱格間的水位差，以保證內隔板的結構安全。

將公式（12）～（16）作為約束條件，hi作為求解變量，各相鄰箱格間的水位差最小為設置目標，利用Excel 自帶的規劃求解功能，即可快速求出滿足條件的hi值，本項目的結果如表1。

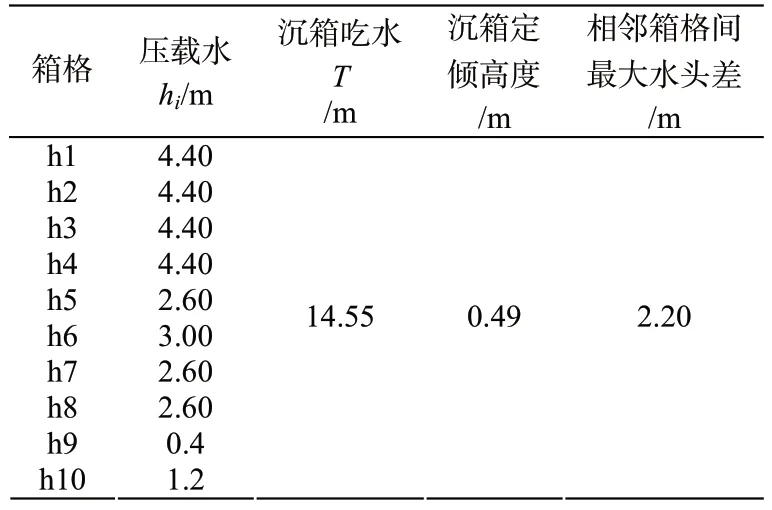
表1 計算所得浮游穩定性參數

本項目參照上述數據進行了兩個異型沉箱的浮運施工，各箱格壓載水高度的理論計算值與現場實施數值基本一致，兩個沉箱均順利完成浮運安裝。

3 結語

對于異型沉箱，因水平截面的非對稱，其幾何屬性的計算較為繁瑣，難以采用手算的方法快速求解，這也異型沉箱浮游穩定計算的難題。在依托項目中，通過理論分析，并借助相關工具，提出了一種簡便高效的解決方法：先利用轉軸公式和慣性矩圓的相關理論，求解截面的最小慣性矩及對應的形心軸；再采用AutoCAD 建模求解異型沉箱的幾何屬性；最后，運用Excel 的規劃求解功能進行數據相關性分析，求解各箱格內所需的壓載水高度。上述方法可高效快捷地解決異型沉箱浮游穩定計算的難題，希望可為類似工程提供借鑒，推進沉箱結構在水運行業的進一步發展應用。