基于遺傳算法優化PID的電磁制熱系統溫度控制方法＊

徐逸揚，潘兆一，李錦鍵

（1.蘭州理工大學電氣工程與信息工程學院，甘肅 蘭州 730050；2.甘肅新農生態能源環保科技有限公司，甘肅 臨洮 730500）

作為一項新型加熱技術，電磁制熱憑借著加熱速度快、熱量利用效率高、安全環保、使用壽命長等優點，現已在農業、工業以及日常生活等多個領域中得到廣泛應用［1］。

常見的電能取暖方式主要有電阻式制熱取暖和電磁制熱取暖。其中，電阻式制熱取暖是利用電流流過導體的焦耳效應產生熱能實現取暖；電磁制熱是利用交變磁場，在鐵質金屬內部形成渦流進而產生熱能實現取暖。但電阻式制熱取暖存在能量損耗大、速度慢、不安全等明顯缺點［2］。相同條件下，電磁制熱取暖的加熱效率可達90%以上，預熱時間相較于傳統電加熱可縮短60%以上［3］。并且電磁制熱取暖具有壽命長、安全可靠等優點。故電磁制熱取暖更優。

目前，許多領域對加熱對象的溫度控制精度要求較高，因此對提高電磁制熱過程中溫度控制的研究具有十分重要的意義。文獻［4］將PID控制與模糊控制理論結合在一起，實現了參數的在線自整定。文獻［5］比較了PID控制與fuzzy－PID控制在穩態誤差、調節時間等方面的特點，通過仿真對比可知，fuzzy－PID控制能夠加快升溫速率，減小系統的超調量，且有更為優良的控制精度。以上文獻均采用模糊控制優化PID參數，有效地控制電磁制熱系統溫度，但沒有結合人工智能算法優化PID參數。

本文從溫度控制策略入手，提出遺傳算法優化增量式PID的電磁制熱溫度控制方法，使得電磁制熱系統加熱速度更快、加熱效果更為均勻，為電磁制熱系統溫度控制技術能夠應用在更廣泛的行業提供實驗分析和參考。

1 電磁制熱溫度控制系統建模

電磁制熱控制系統是由控制器、電磁制熱電源、感應加熱線圈、被加熱層合板及紅外溫度傳感器組成，圖1為電磁制熱控制系統的各個環節的組成模式。

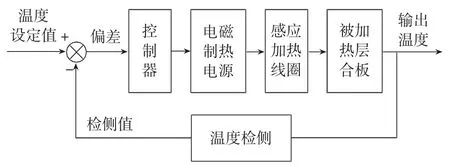
圖1 電磁制熱溫度控制系統

1.1 電磁制熱系統各環節傳遞函數

1.1.1 電磁制熱電源環節傳遞函數

電磁制熱電源的主電路由整流電路和逆變電路構成，如圖2所示。

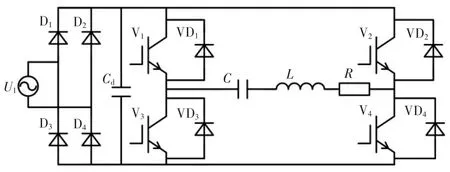
圖2 電磁制熱電源主電路

整流電路的作用是將單相工頻電流整成脈動直流，為逆變電路提供穩定的輸入；再通過逆變電路輸出端為電磁制熱控制系統提供穩定的電源。電磁制熱電源主電路中的逆變環節可以等效成一個增益環節，輸入為直流母線電壓U，輸出為逆變后輸出的有功功率P，在忽略電源擾動的情況下，P的大小與U成正比，其傳遞函數可簡化為：

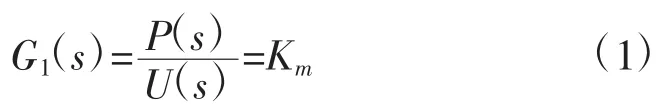
式中，Km為增益。

1.1.2 感應加熱線圈環節傳遞函數

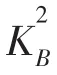
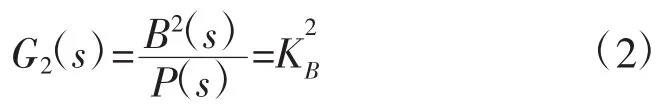
1.1.3 層合板導熱環節的傳遞函數

分析電磁制熱在單位時間內所產生的熱量、材料的密度以及比熱容等物理特性之間的關系，并結合熱力學可得到層合板導熱環節的傳遞函數［7］：

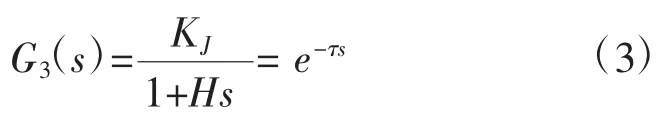
式中，KJ為層合板導熱環節增益；H為電磁制熱時間常數；層合板導熱環節在電磁制熱控制系統中存在滯后特性，所以在當前環節中加入延遲環節e－τs。

1.2 電磁制熱系統溫度控制的傳遞函數

綜上分析電磁制熱系統的電源環節、感應加熱線圈環節及層合板導熱環節，得到電磁制熱系統溫度控制框圖如圖3所示。

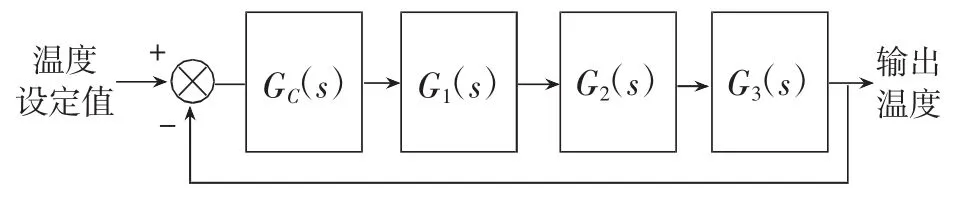
圖3 電磁制熱系統溫度控制框圖

其中：

（1）GC（s）為控制器環節的傳遞函數；

（2）G1（s）為電源環節的傳遞函數；

（3）G2（s）為感應加熱線圈環節的比例系數；

（4）G3（s）為復合材料層合板導熱環節的傳遞函數；

由以上分析可知，感應加熱控制系統的開環傳遞函數為：

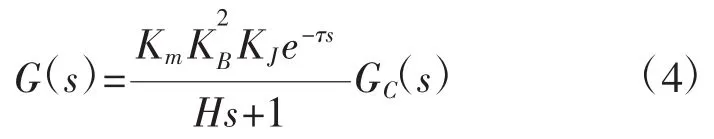
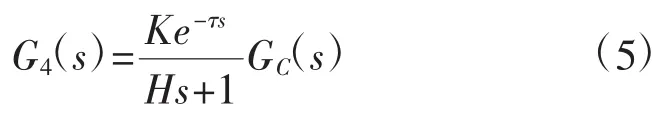
2 電磁制熱溫度控制算法實現

2.1 增量式PID算法簡介

在電磁制熱控制過程中采用增量式PID算法來實現溫度控制，主要為三個參數：比例增益KP、積分時間Ti、微分時間Td。其計算過程如式（6）所示：

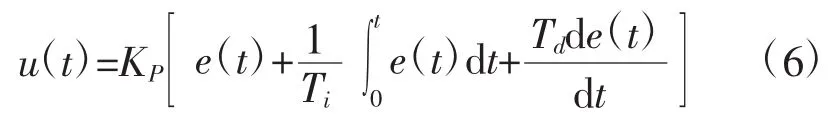
式中，u（t）為控制量；KP為比例控制環節系數；e（t）為系統偏差，e（t）＝yS（t）－yR（t），其中yS（t）為系統設定值，yR（t）為實際測量值；Ti為積分時間環節系數；Td為微分時間環節系數。

將式（6）中u（t）轉化為離散形式u（k），經過整理后，可將第i次采樣時刻控制量的增量Δu表示如下：

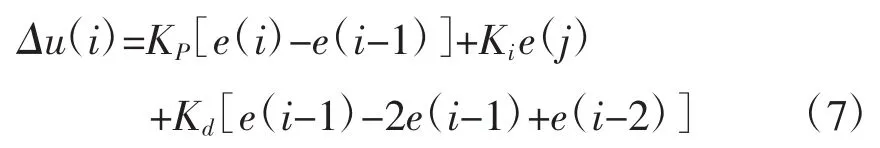
2.2 遺傳算法優化增量式PID

遺傳算法是一種基于生物界進化理論和生物遺傳機制的隨機搜索算法。本文采用遺傳算法優化增量式PID算法中的參數，并應用于電磁制熱系統，以實現對溫度更為有效地控制。

遺傳算法優化增量式PID算法是利用遺傳算法對增量式PID的各個控制參數（Kp，Ti，Td）進行尋優，得到性能指標 J＝g（Kp，Ti，Td）的最優結果。實現遺傳算法優化PID參數需要完成以下四個方面的工作：

（1）參數確定

根據溫度控制的特性，確定參數 Kp，Ti，Td的大概范圍，然后根據參數的精度以及實際情況的要求，對參數進行編碼，并設定遺傳算法的各種初始參數。

（2）選取初始種群

隨機生成初始種群，并產生一定數量的隨機數，設定種群規模。

（3）選取適應度函數

以溫度超調量、溫度調節時間和動態溫度偏差等指標來判斷PID參數是否為最佳。選用式（8）作為優化目標函數［8］：

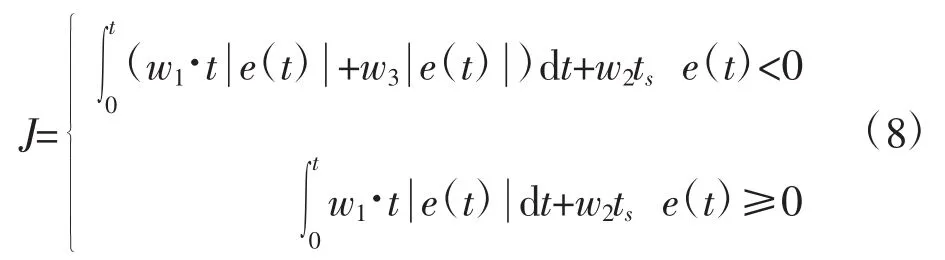
式中，w1，w2，w3為加權系數，且有w3?w1；ts為系統調節時間。

遺傳算法的適應度函數由目標優化函數轉換得到，目標優化函數J值越小，控制系統的質量就越好。故適應度函數為：

（4）種群的復制、交叉與變異

在一個舊種群中選擇生命力強的個體產生新種群的過程稱為復制。本文使用適應度比例選擇法進行復制運算，若某個體的適應度為Fi，則其被選中的概率 Pi為［9］：

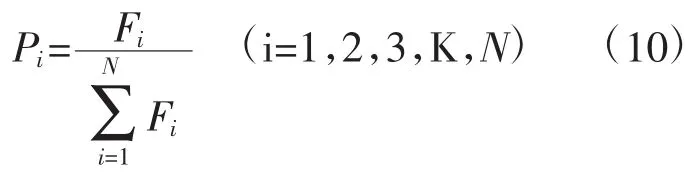
復制運算結束后，由交叉運算和變異運算得到下一代種群，其中，交叉算子概率為Pc，變異算子概率為Pm。在進化后期，為保護已有的優良個體，采取Pc、Pm自適應調整方法［10］，在一定程度上保護了進化后期的最優個體，又降低了局部收斂的可能性。Pc和Pm的動態調整公式為［11］：

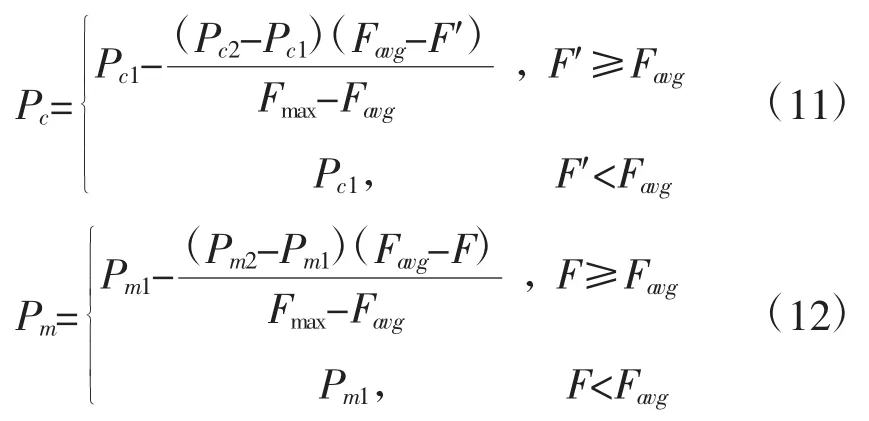
式中，算子概率 Pc1，Pc2，Pm2∈（0，1）；Favg為個體適應度平均值；Fmax為個體適應度最大值；F′為進行交叉的個體中適應度函數值的較大值；F為待變異的個體適應度函數值。

2.3 算法實施的具體流程

遺傳算法優化增量式PID的具體流程如下所示。

（1）設置種群規模M，總進化代數G；設置參數Pc1，Pc2，Pm2，Pm2，w1，w2，w3；初始化進化代數D＝0；

（2）定義參數KP、Ti、Td的范圍，并對KP、Ti、Td進行編碼；

（3）隨機生成規模為M的初始種群；

（4）計算其目標函數優化值以及各個體的適應度；

（5）進行選擇與復制；計算交叉概率，進行交叉運算；計算變異概率，進行變異運算；

（6）進化代數D＝D＋1，得到新種群P（T）；

（7）判斷D是否小于G，若為是，則重復（4）到（6）；若為否，則解碼并輸出最優解。

3 仿真分析

在溫度控制中，輸入變量為溫度偏差，通過對控制器參數進行調整，達到調節電源占空比的目標，進而改變電源輸出功率，最終完成對電磁制熱系統的溫度控制。在控制系統穩定時，功率調節變化較小，且溫度變化較快，一般情況下系統的延時時間為0.5秒。設置加熱最高溫度為45℃，且未加入PID環節，僅在系統中形成閉環控制時，電磁制熱系統升溫曲線仿真結果如圖4所示。

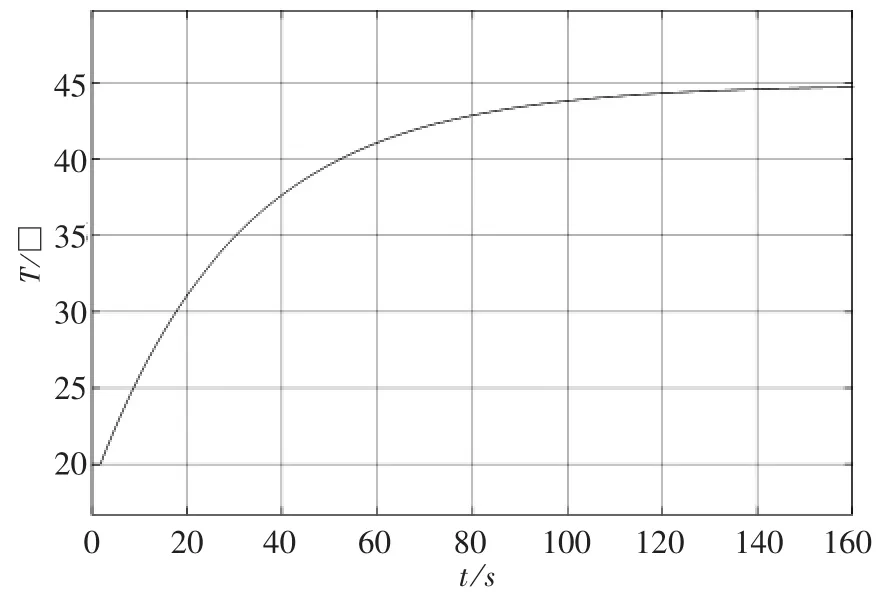
圖4 無PID控制器的電磁制熱系統升溫曲線圖

當電磁制熱系統中采用增量式PID控制時，根據增量式PID控制算法，選取參數為KP＝12.5，Ti＝0.5，Td＝0.1，其升溫曲線仿真結果如圖5所示。

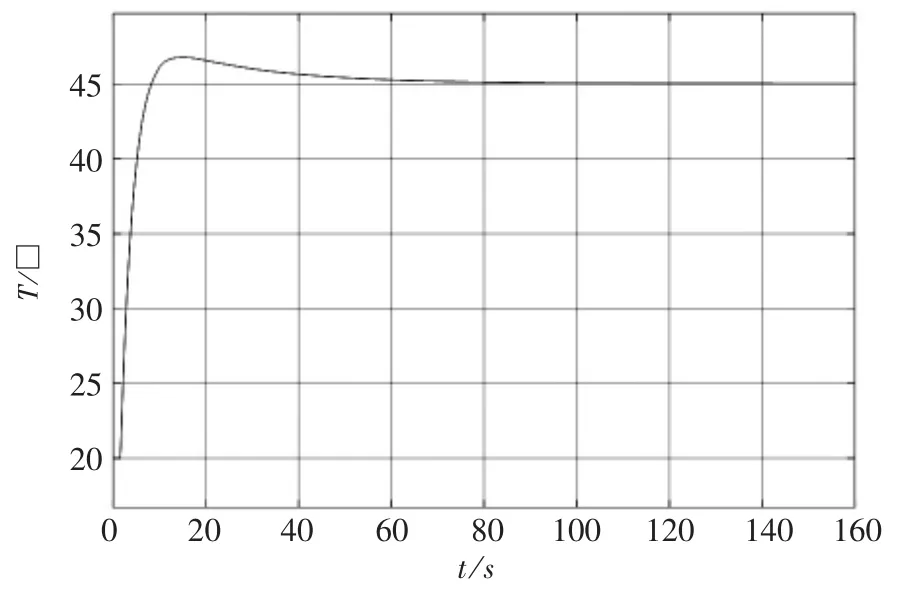
圖5 加入PID后的電磁制熱系統升溫曲線圖

對比圖4和圖5可知：未加入PID環節時，電磁制熱系統溫度雖然在逐步上升，但溫度上升速率較小，進入穩態所需的調節時間較長；加入PID環節后，電磁制熱系統的溫度上升速率顯著提升，且達到穩態溫度所需的調節時間大幅度縮短。

為驗證改進遺傳算法優化PID參數控制策略的優越性，設定總進化代數G＝500，定義參數范圍：KP∈［0，50］；Ti，Td∈［0，3］；經過復制、交叉與變異，在輸出最優結果后進行溫度響應速度模擬測試。

采用遺傳算法優化后，將PID控制器的參數調整為 KP＝40，Ti＝2.5，Td＝0.1，對電磁制熱系統進行仿真，得到升溫曲線，并與圖5的升溫曲線進行對比，得到如圖6所示的升溫曲線對比圖。其中，曲線①為采用遺傳算法優化PID參數前的升溫曲線，曲線②為采用遺傳算法優化PID參數后的升溫曲線。

由圖6可知，采用遺傳算法優化PID參數之后，溫度上升速率得到進一步提升，在達到設定溫度后，會產生一個小范圍的超調量，超調量為4.4%，調節時間為40s。進入穩態后，穩態誤差很小，且穩態溫度基本趨于設定值，上升時間為tr＝4s。由以上仿真結果可知：采用遺傳算法優化增量式PID的溫度控制方法既降低了升溫過程中的超調量，同時又保證了溫度的控制精度。

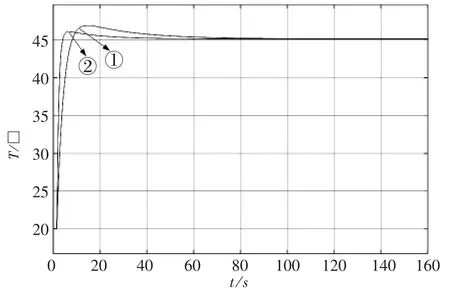
圖6 優化PID參數前后電磁制熱系統升溫曲線

4 結論

本文通過對電磁制熱系統的數學模型進行分析，建立了溫度控制傳遞函數，使用增量式PID算法來實現控制系統的溫度閉環控制，并采用遺傳算法實現對PID參數優化。通過仿真驗證表明：相較于傳統PID算法，采用遺傳算法改進增量式PID后，電磁制熱系統的升溫速率明顯加快、超調量明顯減小、制熱溫度很快進入穩態且穩態誤差很小，穩態溫度基本趨于設定值；采用遺傳算法改進增量式PID實現了對電磁制熱系統的溫度有效控制，在保證電磁制熱系統穩定工作的情況下，能夠準確控制加熱溫度。