注重過程探究 構建有效課堂

文/洪建章

引言

學生學習知識，從理解到掌握再到應用需要一個過程。知識自身也有一個發生、發展和應用的過程。因此，教師不僅要明確知識生成的過程，還要明確教材中練習設置的變化和延伸過程，為學生提供獨立探索的機會。筆者認為，在數學課堂教學中應注重過程探究，使學生對數學產生興趣，激發學生學習的積極性，培養學生掌握知識、運用知識的態度和能力，構建高效的數學課堂。

一、注重知識形成過程探究

問題驅動指引貫穿了學生的數學學習過程。序列問題有助于引導學生了解知識的來龍去脈，經歷知識的發展過程，從而形成對概念、原理等的深刻理解。對過程中蘊含的數學思想的體會與感悟，有助于發展學生的問題意識、探索精神。學生在學習中不僅要知道知識“是什么”，更要清楚“為什么”和“怎么樣”。其中，了解“為什么”和“怎么樣”就體現了對知識邏輯形式的探究。經過這種過程性的探究，學生能夠逐漸明了知識涉及的思維結構和思維方法，將客觀的符號知識內化為個人的認知結構，實現“轉知成智”。在教學中，教師要精心設計探究過程，體現知識的形成過程，讓學生深入理解知識，在運用知識時得心應手，使數學課堂教學更加有效。

例如，在“有理數的乘方”一節中，乘方的意義及求有理數的正整數指數冪是重點和難點，正確理解底數、指數和冪的概念，是正確運算解答乘方的關鍵。對此，筆者在教學過程中設計了三組問題，由淺入深，讓學生通過比較、辨析來理解概念，真正體會冪的運算由來，注重知識的形成過程，真正理解冪的概念。

問題1：把下列各式用乘方的形式表示。

（1）2×2×2×2×2×2=____；

問題2：

（1）在94中，底數是____，指數是____，表示的意義是____________________________；

（2）在（-5）3中，底數是____，指數是____，表示的意義是____________________________。

問題3：53與35的意義相同嗎？與的意義相同嗎？為什么？

注重知識形成的過程，一方面是新課中的知識形成過程，要理解知識的來龍去脈；另一方面是知識體系形成的過程，要理解知識間的區別與聯系[1]。學生在理解的基礎上才能形成結構化的知識，在綜合背景的問題中，才能選擇和調用相應的知識，這樣的數學課堂教學才會更高效。

二、注重解題過程探究

數學習題中有很多極具教學價值的問題，在教學中教師不能僅僅就題論題，給出結果或答案即可，而應充分挖掘題目中的豐富內涵。深度教學要注重學生在教學過程中的切身體會、感受與經驗，豐富學生的過程體驗。這是深度教學的要求，也是對學生學習過程性的回應。因此，教師在教學中應盡量讓學生參與到解題過程探究中，讓學生真正體會習題中包含的知識，快樂地探究學習，使學生不斷完善知識結構和認知結構，培養學生舉一反三、觸類旁通的能力[2]。

以“實際問題與二次函數”這一節的一道習題為例：已知飛機著陸后滑行的距離s（單位：m）關于滑行的時間t（單位：s）的函數解析式是s=60t-1.5t2，求飛機著陸后滑行多遠才能停下來？在講解此習題時，筆者設計了如下的探究過程。

甲同學：準備一架模型飛機，用教室地板當跑道，演示飛機滑行的過程。

乙同學：在黑板上，先建立直角坐標系，t軸表示時間，s軸表示飛機滑行的距離。隨著甲同學的演示過程，在直角坐標系中把圖像畫出來，如圖1所示。

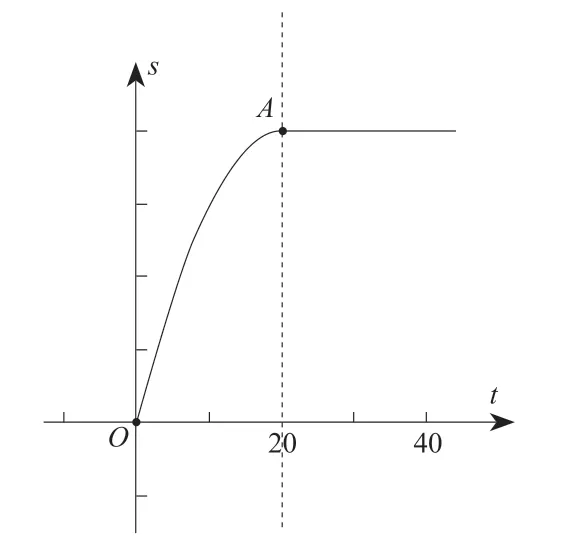
圖1

在這樣的探究過程中，學生真正理解了隨著時間t的增加，飛機滑行的距離s從只有增加不會減少到最終不變的事實，明白了點A的含義，體會了二次函數與實際問題的聯系，達到了對知識的真正理解和應用。

又如，地面上一個小球被推開后開始滑行，滑行的距離s與時間t的函數關系如圖2 中的拋物線所示（A是拋物線的頂點），則下列說法正確的是（ ）。

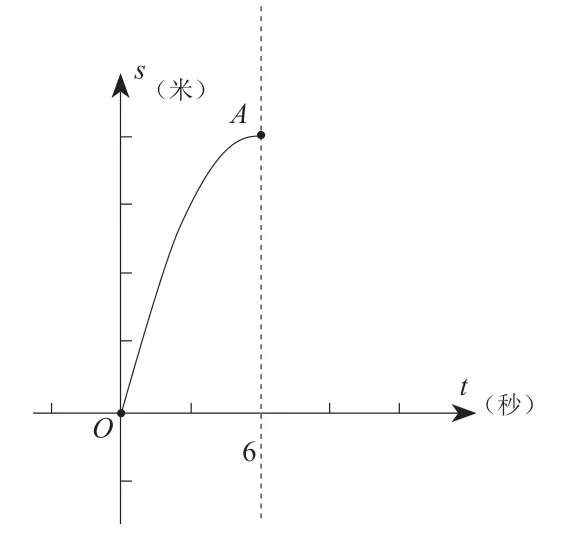
圖2

A.小球滑行6 秒停止

B.小球滑行12 秒停止

C.小球滑行6 秒回到起點

D.小球滑行12 秒回到起點

三、注重知識的重現過程探究

《義務教育數學課程標準（2022年版）》指出，課程內容不僅包括數學的結果，還包括數學結果的形成過程和蘊含的思想方法。對此，教師要重視學生的參與過程，重視知識的重現過程。

例如，在“點和圓的位置關系”這一節中，教師在講解如何確定外接圓的圓心時，可設計如下問題：

問題1：給出一個圓形（大于半圓）紙片，如何確定圓心，并把殘缺的部分補完整？方法1：在紙上用折疊法嘗試，確定圓心，補完圖形，如圖3所示。方法2：利用三角板中的直角及圓周角的性質，如圖4所示。

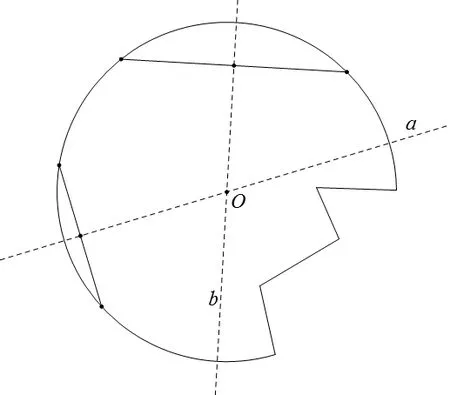
圖3

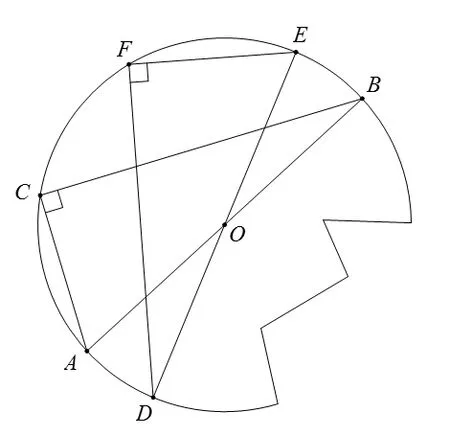
圖4

問題2：撕碎圓形紙片，給碎片定圓心。教師將圓形紙片當著學生的面撕碎(可多撕幾下)，為學生設置一個新的情景：如何確定一塊碎片所在圓的圓心呢？

學生可以利用“過不在同一條直線上的三個點確定一個圓”，即利用外心的性質作圓，找出圓心，補完圖形（如圖5）。

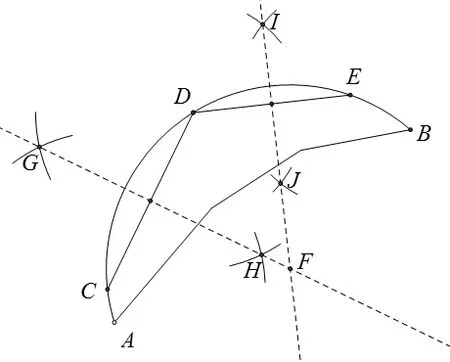
圖5

知識的再現過程有助于學生了解所學知識從何而來、解決何種問題、怎么解決，在有限的時間內探究知識[3]。這樣學生不是被動地接受知識，而是主動獲取知識，獲得真正意義上的學習能力。同時，整個課時也收到了良好的教學效果。可見，有了學生的參與，再現知識過程的探究，課堂教學才會生機勃勃，學生才會成為課堂學習的主體。

四、注重思維過程探究

完整的思維過程包括審題、解題、反思。教師要創造機會讓學生經歷完整的思維過程，讓學生理解數學思維方法、解決問題的策略。教師的主導作用應該體現在選擇好的題目、設計好的問題，以及提煉可推廣的方法、策略或技巧[4]。

以下面一題為例：“若拋物線y=x2+bx（b＞2）上存在關于直線成軸對稱的兩個點，則b的取值范圍是________。”此題考查二次函數與不等式二次函數與一元二次方程的關系、軸對稱的性質、因式分解等知識點。對此，教師可以設計如下探究過程：

問題1：如果點A、點B是關于直線成軸對稱的兩個點，它們有什么特點？（引導學生根據性質設點A（m，n）、點B（n，m））

問題2：點A、點B與拋物線y=x2+bx有什么關系？（引導學生利用待定系數法解決，思路進一步打開）

由（1）-（2）：得n= -b-1-m

代入（1）：得到關于m的一元二次方程：

m2+（b+1）m+（b+1）=0

問題3：存在性與一元二次方程的根有什么關系？（引導學生與一元二次方程根的判別式聯系起來，思路更近一步，慢慢感覺豁然開朗）

Δ=（b+1）2-4（b+1）＞0

即：b2-2b-3＞0

問題4：想一想二次函數圖像與不等式的關系。

此時，令p=b2-2b-3。教師引導學生畫出圖像（如圖6）。

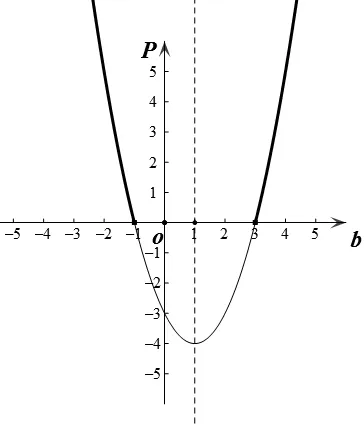
圖6

∵b2-2b-3＞0（即p＞0）

∴b＜-1 或b＞3

又∵b＞2

∴b＞3

注重思維過程探究，可以讓學生真正經歷完整的思維過程，使學生參與審題、析題、解題的探究過程，有利于學生理解數學思維方法，利用數學思想方法找到解決實際問題的策略、技巧，使學習更有效。

結語

正如布魯納所說，“探索是教學的生命線”，這條生命線就是一個個大大小小的過程的集合。在數學課堂教學中，教師要注重知識形成過程探究，注重解題過程探究，注重知識的重現過程探究，注重思維過程探究，使學生更深入地理解知識、掌握知識，真正學會解決問題的方法。