基于進化博弈論的產業創新網絡中非核心企業演化機制研究

于東平，張 慧，胡 鑒，張俊婕

（云南財經大學國際工商學院，昆明 650221）

一、引言

網絡化是當今許多產業尤其是新興產業創新發展的一個重要趨向。所謂創新網絡化，是指企業通過與其他組織、機構或個人建立合作關系以實現其創新目的的一種形式（Fitiar 和Rodriguez-Pose，2013）。由于創新網絡化的發展，一個行業中的企業有了核心與非核心之分。所謂核心企業，是指在某個產業創新網絡中占據引領地位的企業。此類企業往往規模較大，擁有同行企業難以模仿的核心技術（鄧峰，2015），因而是該產業創新的引領者；相比之下，非核心企業因缺乏核心技術，行業影響力較弱，是該行業創新的追隨者或參與者。然而盡管如此，非核心企業的存在卻不容小覷，甚至直接影響著創新網絡的生命力（王偉光等，2017）。更值得關注的是，相較于一般中小企業低迷的創新意愿（何玉潤等，2015）而言，產業創新網絡中的非核心企業，則因網絡中較多的創新資源和較低的創新風險（樊霞等，2010），往往表現出更為活躍的創新行為，甚至可能逆襲成產業內的主導企業（毛蘊詩和鄭奇志，2016），從而為我國諸多中小企業的轉型升級提供了可見的創造性戰略路徑。

適者生存，而非強者生存。在開放式創新背景下，企業間的競爭關系已逐漸轉向競合共贏的博弈關系，從而致使處于創新弱勢地位的非核心企業更加依賴于其所處的創新網絡。創新網絡作為一種組織形式，其本質是聯網行為（Kratzer et al，2005），一般由節點、聯結、資源三要素構成（胡海波等，2020）。考慮到創新網絡節點（創新主體）、聯結（各創新主體間關系）這兩核心要素對網中非核心企業作用結果的權變性，作為產業創新網絡中的非核心企業，有必要諳熟自身所處的創新網絡節點特征及聯結態勢，并據此動態選擇適合自身的創新策略，以期獲得更為突出的網絡創新績效。

然而遺憾的是，以往研究更為關注網絡中核心企業相關研究命題，對網絡中非核心企業的發展問題則關注較少（王偉光等，2017）；即使存在少量的相關研究（張新，2003；Tomlinson 和Fai，2013；張鐘元和李騰，2019），也更傾向于主觀的、思辨的（Hu，2014；Yam et al，2011）、靜態的（戚湧等，2013；吳潔等，2019）剖析，缺乏較為客觀的、推理的、動態的系統性刻畫與仿真過程。

為解密“產業創新網絡背景下非核心企業創新策略選擇”這一實踐黑箱現象，本文嘗試性應用進化博弈論、系統動力學等理論方法，對產業創新網絡中企業之間的互動關系進行刻畫與仿真，并最終給出網中非核心企業創新策略的演化過程。具體而言，本文首先嘗試性運用進化博弈論模型，刻畫出產業創新網絡中非核心企業與核心企業之間的演化歷程，進而求解出非核心企業的演化路徑及進化博弈后的穩定狀態；其次，利用系統動力學Vensim PLE 軟件對產業創新網絡中非核心企業進化博弈過程進行仿真模擬，并找出顯著影響進化穩定結果的關鍵要素；最后，結合上述結果給予相關建議。

二、產業創新網絡中非核心企業與核心企業進化博弈模型構建

由于與一般博弈論（汪旭暉和任曉雪，2020）相比，進化博弈論以有限理性為基礎，以群體（而非個體）為研究對象（Friedman，1998），以持續性博弈為演化依據（付晶等，2018），更符合現實經濟生活中的博弈情形，故而本文將采用進化博弈論對產業創新網絡中非核心企業與核心企業的博弈過程進行刻畫。

（一）基本假設

（1）博弈主體。該進化博弈模型共涉及兩類博弈主體，即產業創新網絡中的非核心企業與核心企業。核心企業處于主導地位，規模大、實力雄厚，并擁有較多的創新技術；非核心企業處于追隨地位，規模小、實力弱，擁有極少量創新技術，但可影響產業創新網絡整體績效。二者均為有限理性的個體，在進行博弈時擁有多種策略選擇的機會。在產業創新網絡中進行初期博弈時，核心企業與非核心企業各自的策略選擇并不一定最優，后期可通過不斷試錯與學習，博弈各方最終均會穩定于某一相對最優策略上。

（2）博弈策略。考慮到產業創新網絡中非核心企業實力較弱，尚不具備突破式或顛覆式創新的能力，故而本文借鑒Zhou et al（2017）的研究成果，認為產業創新網絡中企業可選擇邊際性創新和適應性創新兩種策略。所謂邊際性創新，是以現有技術為基礎，對產品的特征、功能等方面進行微小的改造（Yuan et al，2009）；所謂適應性創新，是為適應消費者行為偏好、政治制度、市場結構、技術水平等環境的變化，通過不斷吸收、整合企業內外部資源，進而改進或創造新的產品（Zhou et al，2017）。非核心企業可通過選擇強創意弱研發、弱創意弱研發等適應性創新策略獲得競爭優勢（徐雨森和徐娜娜，2016）。博弈雙方可依據現有資源和前一輪博弈結果不斷調整博弈策略。

（3）適應度。所謂適應度，原指群體內某種基因存活并遺傳給下一代的相對能力（黃凱南和喬元波，2018），本文特指產業創新網絡中博弈主體的生存和發展能力。博弈主體所獲得的博弈策略收益越高，其所得到的適應度則越大，其所獲得的生存與發展機會則越大。對于產業創新網絡中的非核心企業而言，一方面，其必須具備一定的適應度，才能存活于產業創新網絡；另一方面，產業創新網絡本身的權變性及網中強勢創新主體（核心企業）創新策略的選擇性，均會干擾其適應度。

（二）符號說明

（1）基礎收益。由于非核心企業與核心企業均隸屬于產業創新網絡，所以無論兩者選擇何種創新策略，均會獲得一定的基礎收益。但考慮到兩者在產業創新網絡中地位的差異性，其所獲得的基礎收益應有所差異。故設非核心企業和核心企業選擇任一創新策略的基礎收益分別為U和R。顯然，U ＜R。

（2）創新成本。所謂創新成本，是指概念提出、產品研發、投產銷售等產品創新全過程所產生的一切費用（杜傳忠等，2017），具體包括基礎能力、投入成本和產出成本（由雷和王偉光，2017）。其中，基礎能力是指企業自身的自主研發能力、技術水平、知識吸收等（由雷和王偉光，2017）；投入成本是指企業進行創新活動時所投入的財力和人力成本；產出成本則指新產品投放所需的營銷成本及管理成本（徐立平等，2015）。由于邊際性創新策略僅是在現有技術基礎上進行微小改進，創新成本較小，可忽略不計。因此此處僅需設非核心企業和核心企業選擇適應性創新策略時所產生的創新成本，分別記為P1和P2。顯然，P1＞P2。

（3）創新收益。所謂創新收益，是指因創新而獲得超出創新成本的收益（Pavlou 和Sawy，2011）。設非核心企業和核心企業選擇邊際性創新策略獲得的創新收益分別為M1和M2，顯然M1＜M2；設非核心企業和核心企業選擇適應性創新策略獲得的創新收益分別為W1和W2，顯然W1＜W2。與此同時，考慮到對于同一創新主體而言，其選擇適應性創新策略所獲得的創新收益，通常大于其選擇邊際性創新策略所獲得的創新收益（Narula，2004）。因此可知M1＜W1，M2＜W2；又考慮到創新主體在選擇適應性創新策略時，其所獲得的創新收益常大于其創新成本（Narula，2004）。因此W1＞P1＞0，W2＞P2＞0。

（4）創新沖突損失。考慮到產業創新網絡中的非核心企業與核心企業同時選擇某一相同創新策略時，雙方會因創新相似而產生創新沖突，進而損失一定的創新收益（周珊珊和孫玥佳，2019），故而此處設非核心企業和核心企業因同時選擇適應性創新策略而造成的創新沖突損失分別為V1和V2，顯然V1≥0、V2≥0；由于邊際性創新所實施的創新活動較少，故而本文認為非核心企業與核心企業因同時選擇邊際性創新策略所產生的創新沖突微乎其微，可記為0。

（5）創新概率。設非核心企業選擇適應性創新策略的概率為x，則其選擇邊際性創新策略的概率為1-x。設核心企業選擇適應性創新策略的概率為y，則其選擇邊際性創新策略的概率為1-y。顯然，0 ≤x≤1，0 ≤y≤1 。

（三）模型構建

結合上述假設條件，當產業創新網絡中非核心企業與核心企業進行博弈時，可產生如下四種博弈方式。

（1）當非核心企業和核心企業同時選擇適應性創新策略時，非核心企業和核心企業因此獲得的適應度分別為U+W1-P1-V1和R+W2-P2-V2。

（2）當非核心企業選擇邊際性創新策略、核心企業選擇適應性創新策略時，非核心企業和核心企業因此獲得的適應度分別為U和R+W2-P2。

（3）當非核心企業選擇適應性創新策略、核心企業選擇邊際性創新策略時，非核心企業和核心企業因此獲得的適應度分別為U+W1-P1和R。

（4）當非核心企業和核心企業同時選擇邊際性創新策略時，非核心企業和核心企業因此獲得的適應度分別為U+M1和R+M2。

基于以上分析，本文最終構建了見表1 的產業創新網絡中非核心企業與核心企業的博弈支付矩陣。

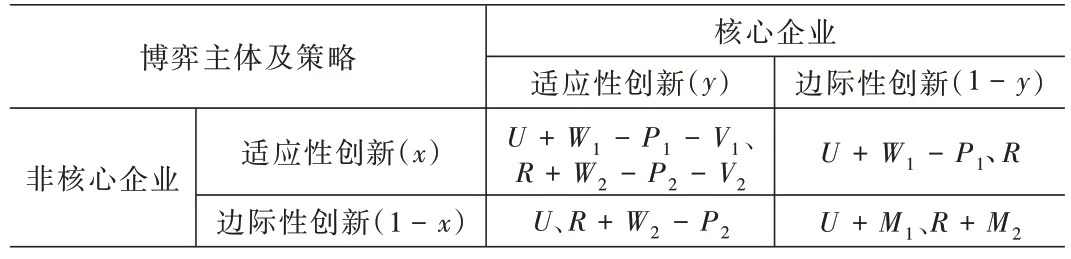
表1 產業創新網絡中非核心企業與核心企業的博弈支付矩陣

三、產業創新網絡中非核心企業與核心企業進化博弈模型分析

（一）博弈主體行為分析

根據表1 中的博弈支付矩陣可得：

非核心企業采取適應性創新策略的適應度為

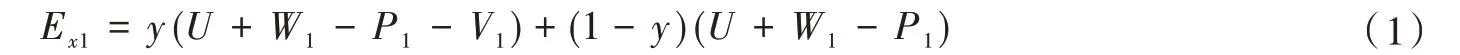
非核心企業采取邊際性創新策略的適應度為

因此，非核心企業在現有策略組合下的平均適應度為

為進一步探究產業創新網絡中非核心企業創新策略選擇的時變性，本文借鑒Bach et al（2006）的研究成果，構建出如式（4）所示的非核心企業復制動態方程式：

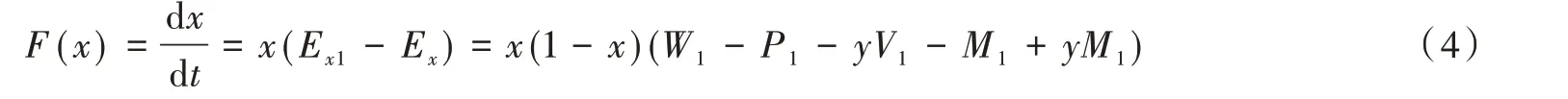
依據進化博弈的進化穩定策略性質（Friedman，1998）可知，只有當F(x)=0，F′(x)＜0 時，非核心企業才處于進化穩定狀態。其中，F′(x) 為復制動態方程F(x)的偏導方程，具體表達式為

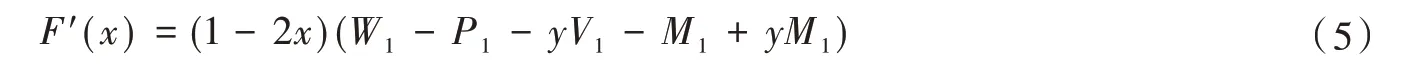
針對非核心企業的復制動態方程F(x)，可進行如下分析：

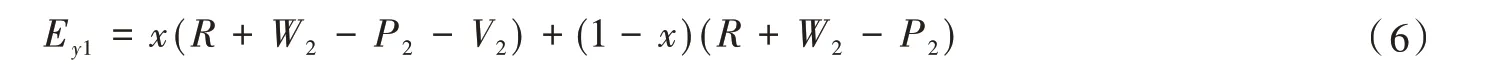
核心企業采取邊際性創新策略的適應度為

因而，核心企業在現有策略組合下的平均適應度為

據此，可以列出如式（9）所示的核心企業的復制動態方程式：

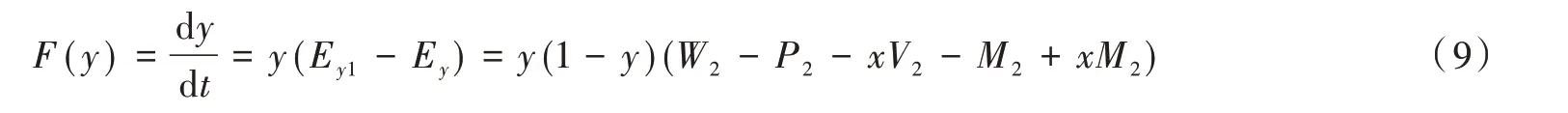
復制動態方程F(y)的偏導方程F′(y)為

針對核心企業復制動態方程F(y)，可進行如下分析：

（二）進化博弈穩定策略分析

為分析出產業創新網絡中創新主體間博弈系統的進化穩定策略，首先令F(x)=0，F(y)=0，計算出產業創新網絡博弈系統的平衡點；其次，借鑒Luthie et al（2005）的研究做法，構建出產業創新網絡中創新主體間進化博弈模型的復制動態雅克比矩陣J；最后，計算出各平衡點的行列式值［記為det(J)］和跡值［記為tr(J)］，并根據Friedman（1998）所提出的進化穩定策略（evolutionary stable strategy，ESS）判斷標準［平衡點的det(J)＞0 且tr(J)＜0］，判定各平衡點是否屬于ESS。其中，產業創新網絡中創新主體間進化博弈模型的復制動態雅克比矩陣J為

利用雅克比矩陣對所計算出的五個平衡點［分別為A（0，1）、B（1，1）、C（1，0）、D（x*，y*）、O（0，0），其中進行局部穩定性分析可知（具體結果見表2），A點（非核心企業選擇邊際性創新而核心企業選擇適應性創新）及C點（非核心企業選擇適應性創新而核心企業選擇邊際性創新）均為進化穩定策略；B點（非核心企業和核心企業均選擇適應性創新策略）及O點（非核心企業和核心企業均選擇邊際性創新策略）均為不穩定的平衡點；D點為鞍點。

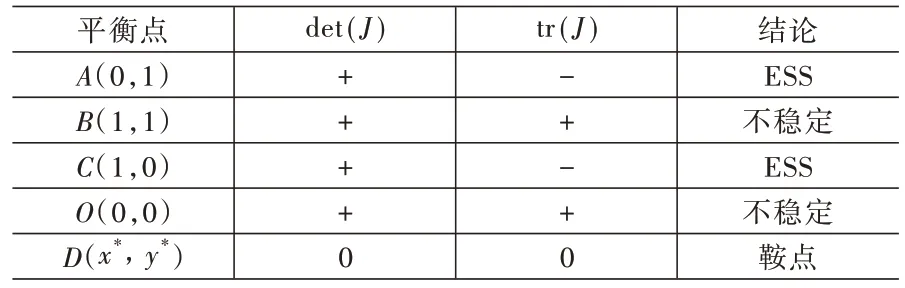
表2 博弈均衡點分析

現以非核心企業選擇適應性創新策略的概率x為橫坐標，以核心企業選擇適應性創新策略的概率y為縱坐標，最終可構建出如圖1 所示的兩者間的進化博弈動態演化圖。

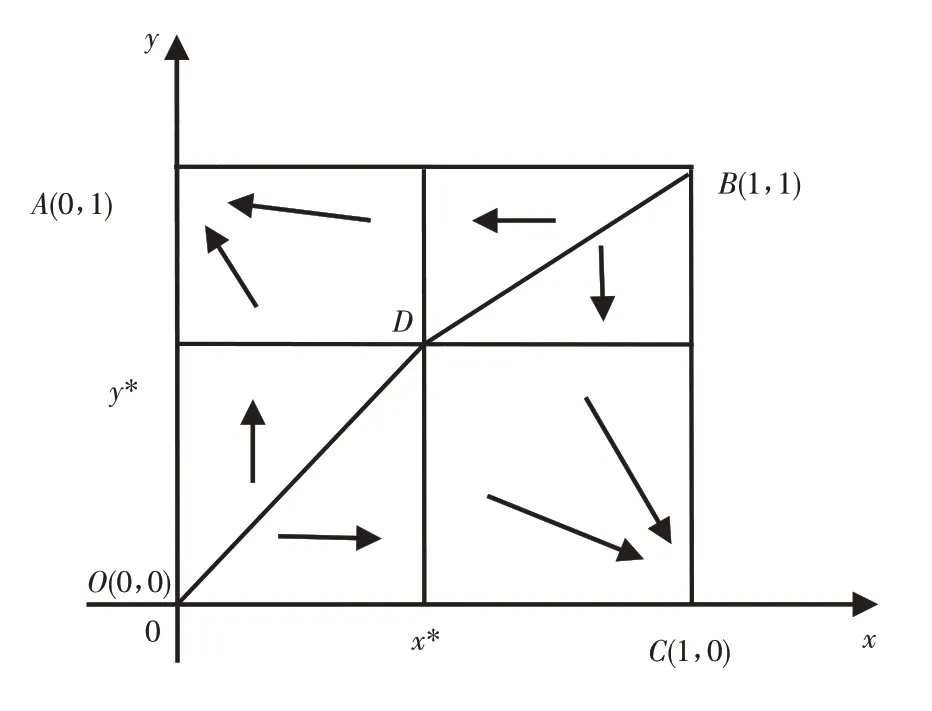
圖1 非核心企業與核心企業進化博弈動態演化圖

由圖1 可知，創新策略的初始被選概率，決定了產業創新網絡中非核心企業和核心企業進化博弈最終收斂的穩定狀態。更為確切地說，若初始點（x，y）位于圖形BDOA范圍內，則博弈將最終收斂于A點；若初始點（x，y）位于圖形BCOD范圍內，則博弈將最終收斂于C點。因此，若圖形BDOA的面積得以擴大，即選擇適應性創新策略的核心企業增加，選擇適應性創新的非核心企業數量減少，最終則會導致核心企業群實力越來越強，非核心企業群則相對更加弱小。為避免實力差距所導致的各種經濟風險（鄭燁和吳建南，2017），應盡可能增加圖形BCOD的面積，也即增加選擇適應性創新策略的非核心企業的數量。考慮到圖1 中的A、B、C、O均為固定點，故而圖形BCOD的面積大小僅取決于D點的位置。故而，當D點向左上方移動時，BCOD的面積才會增大。也就是說，為保持產業創新網絡的均衡發展，必須提高非核心企業選擇適應性創新策略的創新收益W1，減少其選擇適應性創新策略的創新成本P1和創新沖突損失V1。

四、產業創新網絡中非核心企業與核心企業進化博弈的模擬

考慮到系統動力學（system dynamics，SD）在推演不完全信息系統時的理論優勢（鄧建高等，2020）及其在刻畫創新博弈行為時的方法優勢（鄭彤彤和謝科范，2015），將應用其對產業創新網絡中非核心企業與核心企業創新策略選擇的博弈過程進行仿真模擬，具體如圖2 所示。其中，涉及2 個水平變量（非核心企業選擇適應性創新策略的概率x，核心企業選擇適應性創新策略的概率y）、2 個速率變量［流速F(x)、流速F(y)］、4 個輔助變量（分別為非核心企業選擇適應性創新策略和邊際性創新策略的適應度Ex1和Ex2，核心企業選擇適應性創新策略和邊際性創新策略的適應度Ey1和Ey2）及10 個常量（分別為非核心企業和核心企業創新的基礎收益U和R，適應性創新收益W1和W2，適應性創新成本P1和P2，創新沖突收益損失V1和V2，邊際性創新收益M1和M2）。

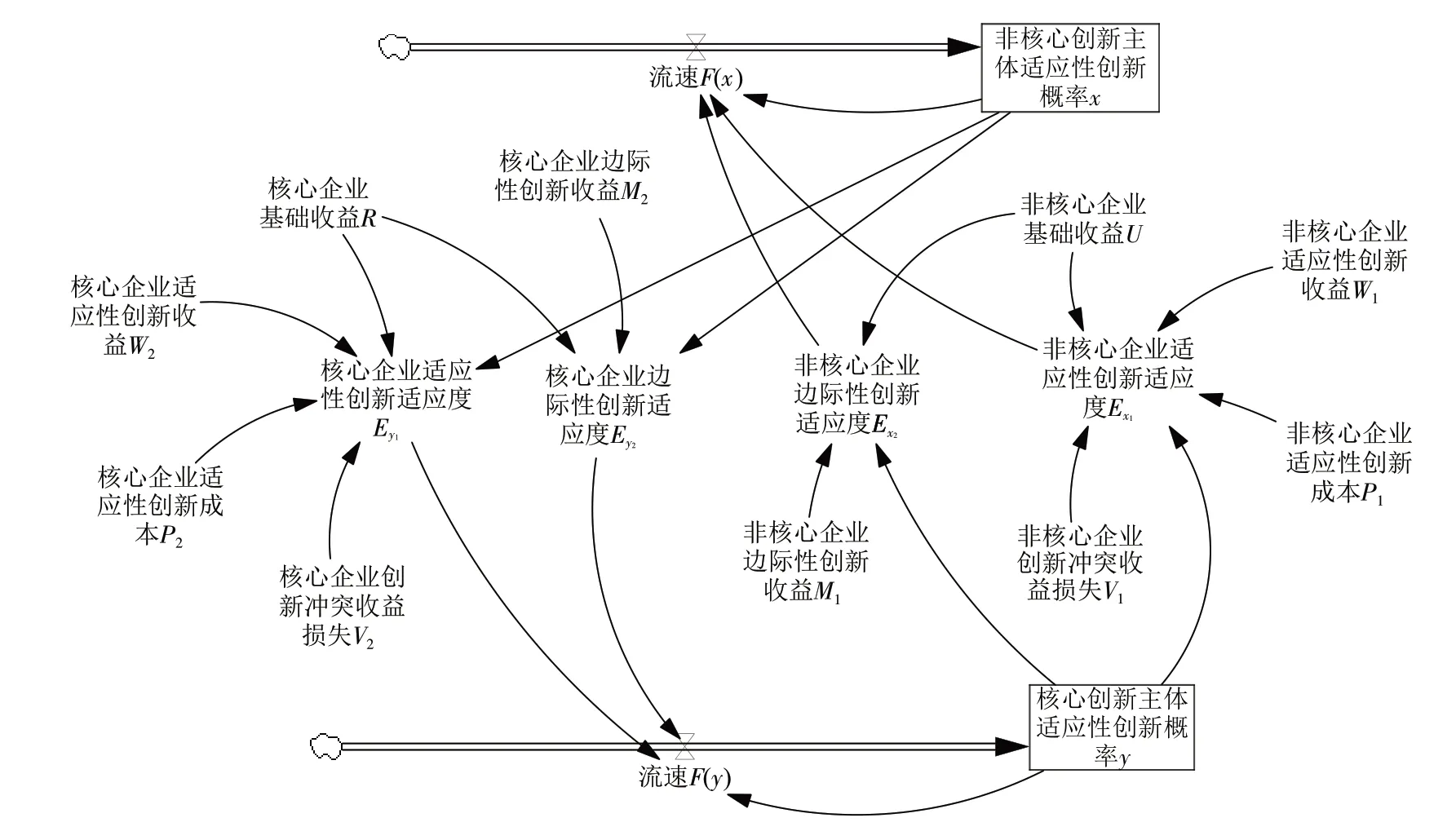
圖2 產業創新網絡中非核心企業與核心企業SD 仿真演化模型

結合前文所推演的博弈過程及已有文獻中的初始值設定方法（具體賦值情況見表3），借鑒流率基本入樹建模法（冷碧濱等，2017）對產業創新網絡中非核心企業與核心企業的博弈過程進行仿真（具體如圖3所示）。設定仿真模型初始時間為0，結束時間為30，時間單位為年。

表3 仿真模型的變量初始值

（一）產業創新網絡系統動態仿真

由圖3 可知，在短期內非核心企業選擇適應性創新的概率從初始值0.5 迅速上升至最高點（0.7 左右），后快速下降至0，并從第6 年開始一直保持在0 的狀態；而核心企業選擇適應性創新策略的概率則由初始點0.5急劇上升至1，后一直保持在1。針對這一現象可能的解釋是，考慮到適應性創新策略收益性較高，故而在初次博弈時非核心企業與核心企業均傾向于選擇此創新策略，進而表現出短期內此策略選擇概率迅速升高的表象。然而數次博弈后，非核心企業逐漸發現其選擇適應性創新策略的收益小于其選擇邊際性創新收益策略的收益，故而隨后逐漸轉向選擇邊際性創新策略。然而，與非核心企業相反的是，核心企業在前期的多次博弈中，明顯感知到選擇適應性創新策略時的良好收益，故而后期會逐漸固定在此策略上。

通過計算可得，D點的坐標為。將D點帶入圖1 所示的進化博弈動態演化圖中可知，初始點（0.5，0.5）位于BCOD范圍內。結合前文的ESS 分析結果可知，產業創新網絡系統理應最終收斂于C點（非核心企業選擇適應性創新，而核心企業選擇邊際性創新），這恰好與圖3 所示的演化結果相悖。為解釋其原因，應用系統動力學軟件，最終給出了如圖4 所示的理論與實際演化差異圖。從中可以看出，實際演化中的ODB為一條平滑向上的曲線，初始點（0.5，0.5）位于BAOD范圍內（而非理論上認為的BCOD范圍內），故而最終收斂于A點（而非理論上認為的C點）。

圖3 初始狀態下非核心企業與核心企業適應性創新概率演化圖

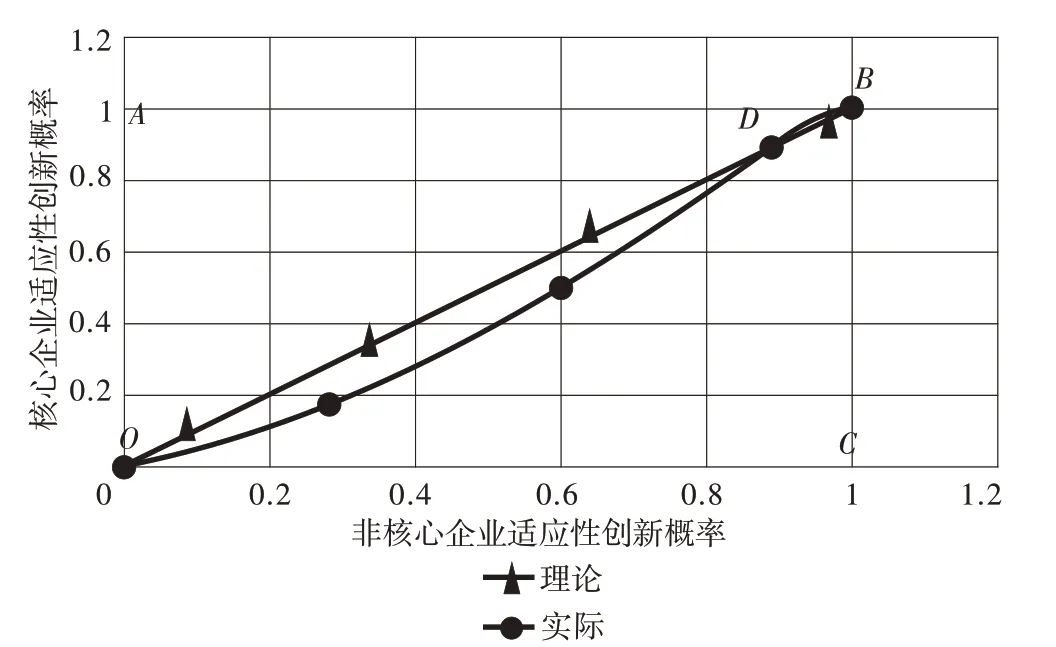
圖4 理論較實際演化差異圖

（二）策略被選初始概率對演化結果的影響分析

為判別策略被選初始概率對產業創新網絡系統演化結果的差異性影響，嘗試性對兩種情況下的系統演化結果進行比較，最終得到了圖5～圖8 所示的演化路徑圖。

情況一：保持核心企業適應性創新策略被選概率y初始值0.5 不變，判斷非核心企業適應性創新策略被選概率x初始值對系統演化結果的影響。

如圖5 和圖6 所示，當x的初始值分別為0.1、0.3、0.5（分別對應x-Current1、x-Current2、Current）時，概率x則表現出先短暫上升后下降，最終穩定于0 的演化趨勢，而概率y則表現出先急速上升，后收斂于1 的演化趨勢，并且x初始值越小，y的收斂速度越快；當x的初始值分別為0.7、0.9（分別對應x-Current3、x-Current4）時，概率x則表現出先迅速上升后穩定于1 的演變趨勢，而概率y則表現出先上升后急劇下降，最終穩定于0 的演變趨勢，并且x初始值越大，y的收斂速度越快。綜上可知，非核心企業選擇適應性創新策略的概率對系統演化結果影響較大。更為確切地說，當x＞0.5 時，系統演化結果將最終穩定在非核心企業選擇適應性創新而核心企業選擇邊際性創新的狀態；當x≤0.5 時，系統將最終穩定在非核心企業選擇邊際性創新而核心企業選擇適應性創新的狀態。

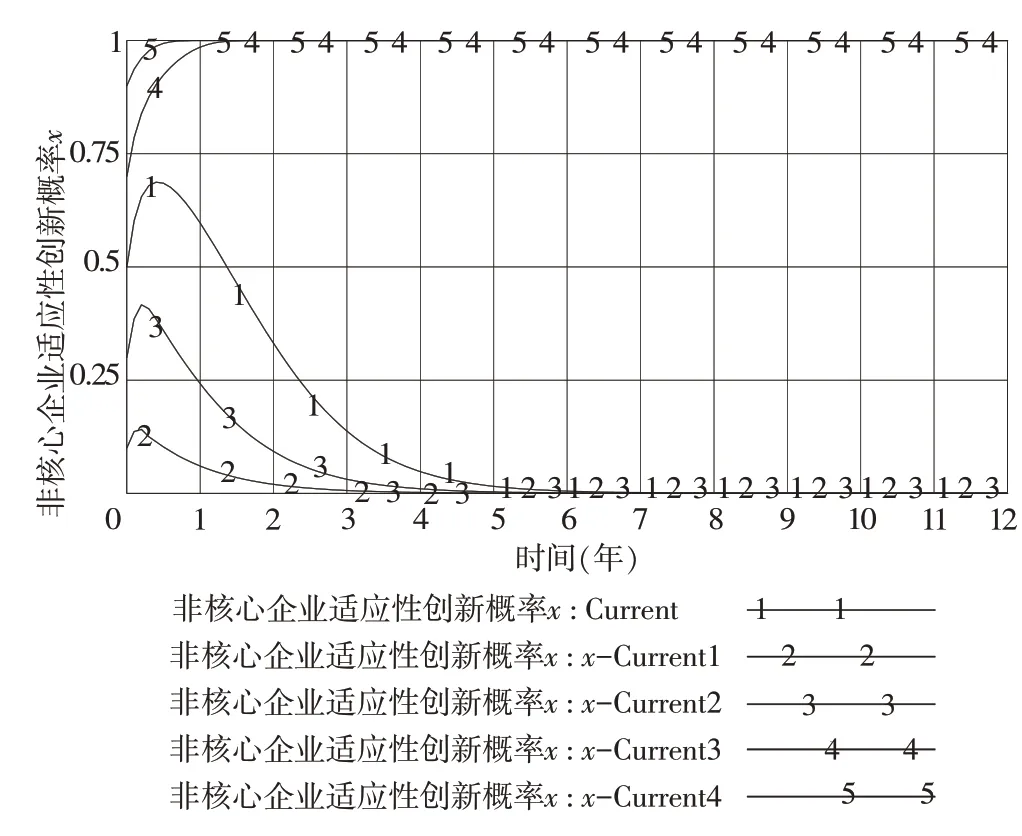
圖5 x 初始值的變化對概率x 的演變影響

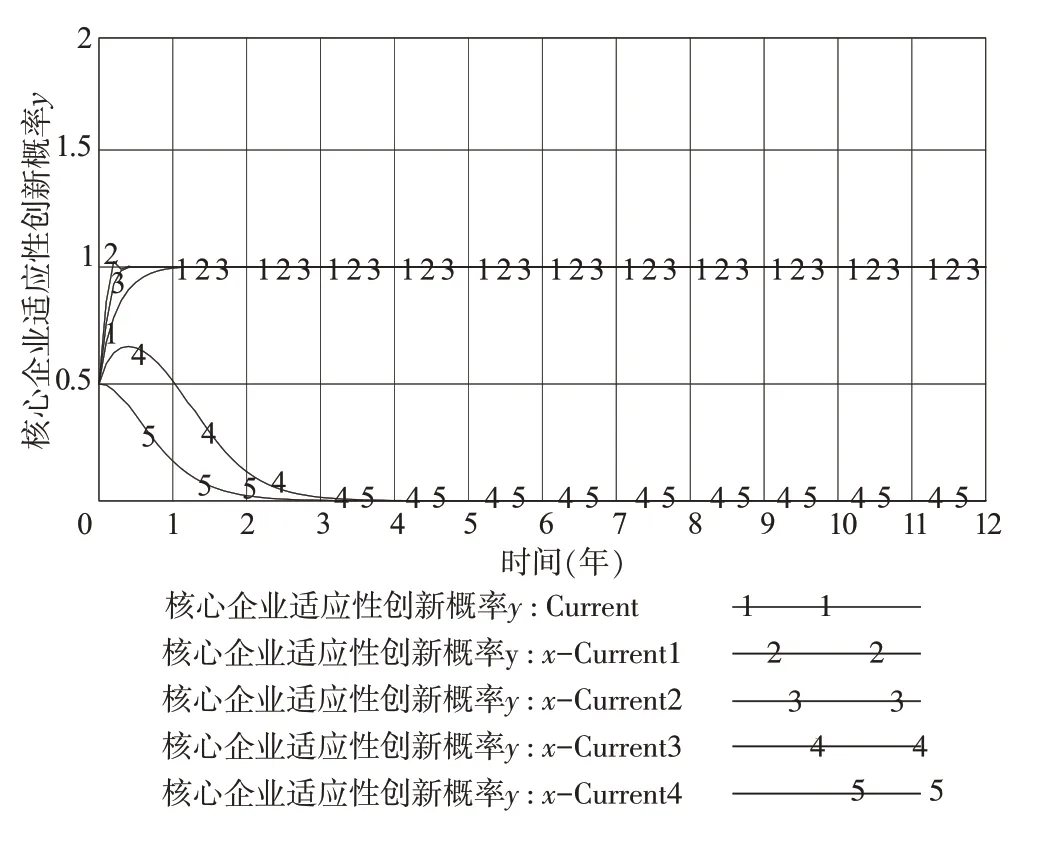
圖6 x 初始值的變化對概率y 的演變影響

情況二：保持非核心企業適應性創新策略被選概率x初始值0.5 不變，判斷核心企業適應性創新策略被選概率y初始值對系統演化結果的影響。

如圖7 和圖8 所示，當y的初始值分別為0.1、0.3（對應y-Current1、y-Current2）時，概率x則表現出急劇上升后穩定于1 的狀態，而概率y則表現出先上升后驟降至0 并保持穩定的狀態；當y的初始值分別為0.5、0.7、0.9（對應Current、y-Current3、y-Current4）時，概率x則表現出先上升后驟降至0 并保持穩定的狀態，而概率y則表現出急劇上升后穩定于1 的狀態，并且y值越大，x的收斂速度則越快。綜上可知，核心企業選擇適應性創新策略的概率初始值對博弈系統進化結果影響顯著，即當y≥0.5 時，系統演化結果將最終穩定在核心企業選擇適應性創新而非核心企業選擇邊際性創新的狀態；而當y ＜0.5 時，系統將最終穩定在核心企業選擇邊際性創新而非核心企業選擇適應性創新的狀態。

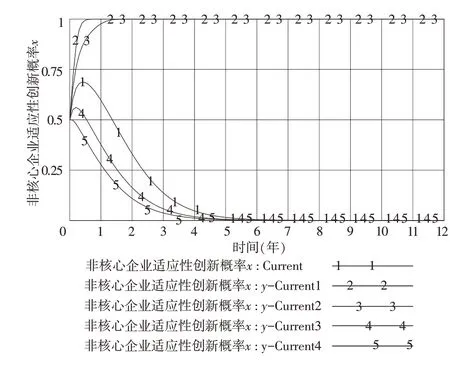
圖7 y 初始值的變化對概率x 的演變影響

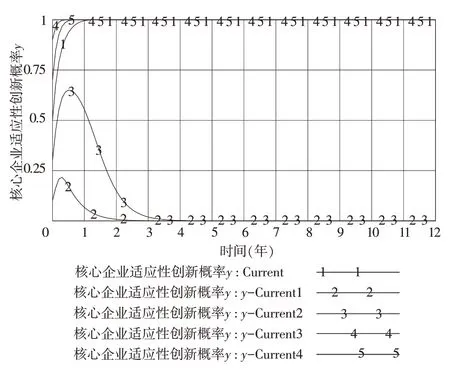
圖8 y 初始值的變化對概率y 的演變影響

結合上述兩種情況可知，產業創新網絡中非核心企業與核心企業進化博弈的穩定策略為（適應性創新，邊際性創新）或（邊際性創新，適應性創新）。具體而言，當初始點為（x≤0.5，y=0.5）或（x=0.5，y≥0.5）時，由于其均位于圖形BDOA范圍內。因此系統最終將穩定在非核心企業選擇邊際性創新而核心企業選擇適應性創新的狀態，并且x值越小、y值越大，系統收斂的速度則越快；當初始點為（x＞0.5，y=0.5）或（x=0.5，y ＜0.5）時，由于其均落在圖形BCOD范圍內。因此系統最終將收斂于非核心企業選擇適應性創新而核心企業選擇邊際性創新的狀態，并且x值越大、y值越小，系統收斂速度則越快。

（三）敏感性分析

為判斷產業創新網絡中非核心企業演化結果的敏感性，將分別調整適應性創新收益、適應性創新成本及創新沖突損失這三個變量的取值，以觀察其對演化結果的影響程度。

圖9 展示了不同創新收益W1水平下非核心企業選擇適應性創新策略概率x的敏感性。其中，曲線Current 表示創新收益為初始狀態（W1=28）時概率x的演化結果，曲線Current1 表示創新收益減1（W1=27）時概率x的演化結果，曲線Current2 表示創新收益增1（W1=29）時概率x的演化結果，曲線Current3 表示創新收益增2（W1=30）時概率x的演化結果。與曲線Current 對比可知，當創新收益微減時，非核心企業選擇適應性創新策略的概率x將以更快的速度收斂于0（非核心企業最終收斂于選擇邊際性創新策略），而當創新收益增1 時，非核心企業選擇適應性創新策略的概率x則將以較快速度收斂于1，而當創新收益增2 時，非核心企業選擇適應性創新策略的概率x則將以更快速度收斂于1。由此可知，非核心企業選擇適應性創新策略的決策受創新收益的影響較為敏感。當創新收益降低時，非核心企業將最終收斂于選擇邊際性創新策略；但只要創新收益有所提升，非核心企業則將快速選擇適應性創新策略。

圖9 創新收益變動對概率x 的敏感性

圖10 則給出了不同創新成本取值（分別賦值為7.8、8.8、9.8、10.8，對應于曲線Current2、Current1、Current、Current3）時非核心企業適應性創新策略被選概率x的演化路徑。由圖10 可知，與初始狀態（創新成本為9.8時）相比，創新成本每減少1，非核心企業選擇適應性創新策略的概率x則以更快速度收斂于1；然而，當創新成本增加1 時，非核心企業選擇適應性創新策略的概率x則以較快速度收斂于0，并最終穩定在邊際性創新策略的狀態。由此可知，創新成本的變動對非核心企業選擇適應性創新策略的決策影響也較為顯著。當創新成本降低時，非核心企業將以較快速度收斂于選擇適應性創新策略；但只要創新成本有所上漲，非核心企業則將快速收斂于選擇邊際性創新策略。

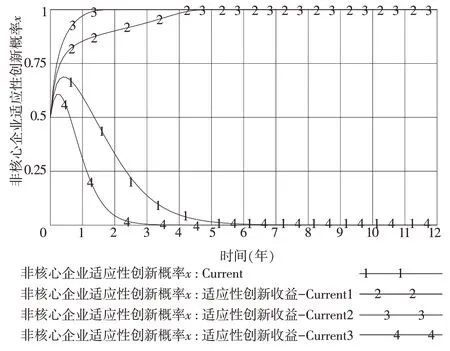
圖10 創新成本變動對概率x 的敏感性

圖11 則展示了不同創新沖突損失取值（分別為17.3、18.3、19.3、20.3，對應曲線Current3、Current2、Current、Current1）下非核心企業選擇適應性創新策略概率x的演化趨勢。由圖11 可知，與初始狀態（創新沖突損失為19.3 時）相比，當創新沖突損失增加1時，非核心企業選擇適應性創新策略的概率x將以較快速度聚斂于0；而當創新沖突損失值逐漸縮減時，非核心企業選擇適應性創新策略的概率x收斂于1的速度則將大大加快。由此可知，非核心企業選擇適應性創新策略的決策行為也受創新沖突損失影響。當創新沖突損失有所增加時，非核心企業則將快速收斂于選擇邊際性創新策略；但只有當創新沖突損失減少至足夠多時，非核心企業才會最終收斂于適應性創新策略。

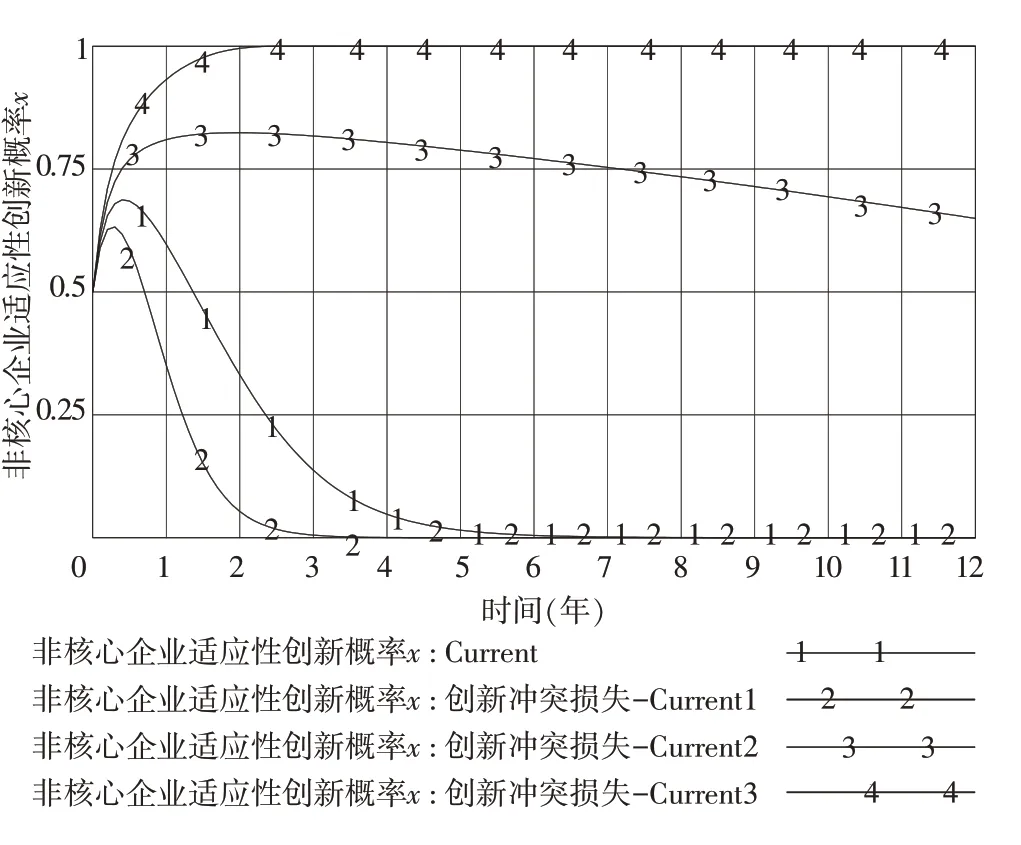
圖11 創新沖突損失變動對概率x 的敏感性

五、結論與討論

（一）研究結論

為解密“產業創新網絡背景下非核心企業創新策略選擇”這一實踐黑箱現象，嘗試性應用了進化博弈論、系統動力學等理論方法，對產業創新網絡中非核心企業與核心企業之間創新策略選擇的博弈過程進行了刻畫與仿真，并最終得出了如下結論：

第一，選擇不同于彼此的創新策略，是產業創新網絡中非核心企業與核心企業進化博弈的穩定策略。通過對比A、B、C、D、O五個平衡點可知，僅A點（核心企業選擇適應性創新、非核心企業選擇邊際性創新）和C點（核心企業選擇邊際性創新、非核心企業選擇適應性創新）為進化穩定策略，即雙方需選擇不同于彼此的創新策略，才能實現產業創新網絡的均衡發展。

第二，各創新主體選擇創新策略的初始概率，將直接決定產業創新網絡進化博弈結果。如前所述，當非核心企業和核心企業選擇適應性創新策略的初始概率（x，y）位于圖形BCOD內時，則系統最終將收斂于非核心企業選擇適應性創新而核心企業選擇邊際性創新的狀態；而當初始概率（x，y）位于圖形BDOA內時，則系統最終收斂于非核心企業選擇邊際性創新而核心企業選擇適應性創新的狀態。

第三，創新收益、創新成本及創新沖突損失的變動，均會顯著干擾非核心企業適應性創新策略的選擇。敏感性分析結果顯示，創新收益、創新成本和創新沖突損失的變動，均對產業創新網絡中非核心企業選擇適應性創新策略的概率x具有顯著影響。

（二）創新點

圍繞“產業創新網絡背景下非核心企業創新策略選擇”這一切入點，應用進化博弈論、系統動力學等方法，以期剖析其在與核心企業進化博弈中的創新策略動態選擇過程，其創新點主要體現在選題視角的新穎性上。盡管近年來學者們已逐漸認知到創新網絡化現象的存在及其價值，并紛紛圍繞創新網絡的整體特征刻畫、網內核心企業的識別、評價及優勢等內容開展了大量的研究工作，但對網內非核心企業及其相關發展問題缺乏系統性關注。緊扣這一特殊群體，分析其在與網內核心企業進化博弈中的創新策略動態選擇過程，以期為我國諸多中小企業的轉型升級提供創造性戰略路徑。

（三）研究啟示

一是積極發揮市場及政府調節作用，引導非核心企業選擇合適的創新策略。如前所述，產業創新網絡中非核心企業與核心企業之間的進化博弈結果將最終收斂于雙方選擇不同于彼此的創新策略。為此，為促進產業創新網絡和諧、健康、持續發展，還應充分發揮市場及政府部門的調節作用，適時引導網中企業的創新策略選擇行為。當網中核心企業適應性創新積極性不高，產出能力不足時，可適當采用稅收優惠政策、創新激勵制度、技術扶持政策等手段，激勵網中非核心企業適時開展適應性創新行為；而當網中核心企業適應性創新氛圍活躍，產出較高時，則可適當引導非核心企業選擇邊際性創新策略，以合理規避創新沖突損失，并為后續博弈儲備力量。

二是集多方力量，切實加強非核心企業適應性創新能力建設工作。如前所述，非核心企業選擇適應性創新的決策行為受創新收益、創新成本及創新沖突損失顯著影響，這一定程度上反映出非核心企業選擇適應性創新策略的步伐并不堅定，易受外界因素干擾，也從另一側面映射出其尚未成熟的適應性創新能力。故而，政府部門應集結多方力量，切實有效地加強網中非核心企業適應性創新能力建設工作。具體而言，除給予必要的財務、技術等扶持性政策外，政府部門還應對部分典型非核心企業進行實地調研，切實了解其發展困境，并可集結網中核心企業、社會組織等多方力量及時開展更具針對性的幫扶工作。

（四）研究展望

為深入挖掘出產業創新網絡中非核心企業的生存之道，以便為諸多中小企業創新轉型提供路徑參考，結合進化博弈論和系統動力學相關知識，系統刻畫并仿真了產業創新網絡背景下非核心企業與核心企業互動下的創新策略進化博弈過程。當然，仍存在以下不足，望后期能進一步探討：一是研究內容上并未考慮多元化網絡情境對非核心企業創新策略選擇的權變影響。由于非核心企業的創新策略選擇一定程度上也受制于產業創新網絡系統本身狀態特征的動態變化，因此后期可嘗試性探討非核心企業在與多元網絡情境互動下的創新策略權變選擇機制。二是研究方法上側重于模擬仿真，欠缺實證研究或案例研究結果的互證。為刻畫非核心企業與核心企業的進化博弈過程，采用了進化博弈論及系統動力學相關知識，但仍缺乏更有力的實踐資料進行互證。為此，后期可增加規范式實證研究或扎根式案例研究，從而充分夯實所研內容的科學性。