探析極值點偏移證明問題的解決方法

山東濱州市無棣縣第二高級中學（251900） 徐景超

所謂極值點偏移，指的是連續函數f(x) 在(x1,x2)(f(x1)=f(x2)為前提)上的極值點左右增減速度不同導致極值點x0≠的情況出現。與其有關的問題主要有，一是與極值點偏移的不等式證明問題，二是極值點偏移對應的極值差范圍的求解。這些問題與函數單調性、極值和最值等知識點都有密切的聯系。其中，有關極值點偏移證明問題更為常見。掌握這類問題的解決方法，有助于學生開拓思路，有效破解難度較大的函數問題。

一、對稱變換

采用對稱變換方法解決有關極值點偏移證明問題，關鍵在于把問題中的兩個變量對稱分布在不等號的兩邊，進一步構造函數把問題轉化為函數最值問題。如求證x1+x2＞2x0，可構造函數g(x)=f(x0+x)-f(x0-x) 或g(x)=f(x)-f(2x0-x) 等 對稱形式，探究g(x) 的單調性，進而把問題轉化為極值點之間的關系。具體解題步驟如例1所示。

［例1］已知函數f(x)=-x+(x+2)lnx(x∈R)，且函數f(x)圖像在A(x1,f(x1))、B(x2,f(x2)) (x1＜x2)兩個不同點處的切線互相平行，求證x1+x2＞4。

分析：對問題中所給“不同點處切線互相平行”進行分析可得，該兩點處對應導數相等。問題所求證的不等式中含有兩個變量，即x1、x2，因此需要對不等式進行變形，使兩個變量對稱分布在不等號的兩邊，即x1＞4-x2，構造函數g(x1)-g(4-x2)，并探究其單調性，從而證明x1+x2＞4成立。

證明：∵f(x)=-x+(x+2)lnx(x∈R)，

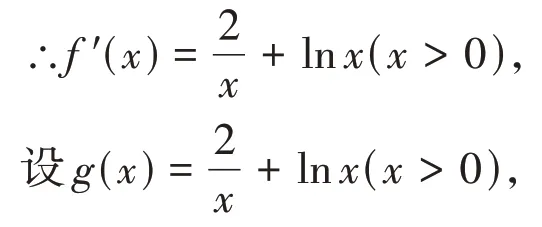
由題意“函數f(x) 的圖像在A(x1，f(x1))、B(x2，f(x2)) (x1＜x2)兩個不同點處切線互相平行”可得，f′(x1)=f′(x2)，即g(x1)=g(x2)，

∵g′(x)=-∴g(x)在(0,2) 上單調遞減，在(2,+∞)上單調遞增，

∵g(x1)=g(x2)，∴必 有0 ＜x1＜x2＜2，4-x1＞2，

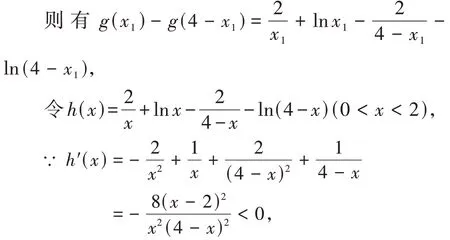
∴h(x)在(0,2)上為減函數，h(x)＞0，

∴g(x1)-g(4-x1)＞0，即g(x1)＞g(4-x1)，g(x2)＞g(4-x1)，

∵g(x)在(2,+∞)上單調遞增，∴x2＞4-x1，即x1+x2＞4。

評析：對稱變換是解決極值點偏移證明問題的常見方法之一。不同的不等式證明有著不同的變換形式，類似x1±x2＞2x0形式的證明，可通過加減使其對稱，而類似x1·x2＞2x0形式的證明，往往通過乘除變換得到對稱形式。

二、消參減元

消參減元主要是建立參數和極值點的聯系等式，通過消去參數或減少變量個數對問題進行求解。解決極值點偏移證明問題時，首先令函數的導函數f′(x0)=0，根據f′(x0)=0 找到并建立極值點與方程系數的關系，再利用作差的形式消去參數或減少變量個數，如f(x)=axb+m（a、b為常數，m為參數）可以轉化為f(x1)-f(x2)消去參數m再求解；其次根據消參后的式子構造對應的函數；最后探究所構造的函數的單調性、極值、最值等，從而解決問題。具體解題步驟如例2所示。

［例2］已知函數f(x)=x2+2x-2 lnx，若方程f(x)=x2+2m有兩個不相等的實數根x1，x2，求實數m的取值范圍并證明：x1x2＜1。

證明：由題意可得方程f(x)=x2+2m等價于x-lnx-m=0，

令g(x)=x-lnx-m(x＞0)，則g′(x)=1-當x∈(0,1) 時，g′(x)＜0，g(x)單調遞減；當x∈(1,+∞)時，g′(x) ＞0，g(x)單調遞增，所以g(x)min=g(1)=1-m。

若方程f(x)=x2+2m有兩個不相等的實根，則有g(x)min＜0，即m＞1，

當m＞1 時，0 ＜e-m＜1 ＜em，g(e-m)=e-m＞0，g(em)=em-2m，

令h(x)=ex-2x(x) ＞1，則h′(x)=ex-2 ＞0，h(x)在(1,+∞)上是增函數，h(x) ＞e-2 ＞0，∴g(em)=em-2m＞0，即m的取值范圍為(1,+∞)，

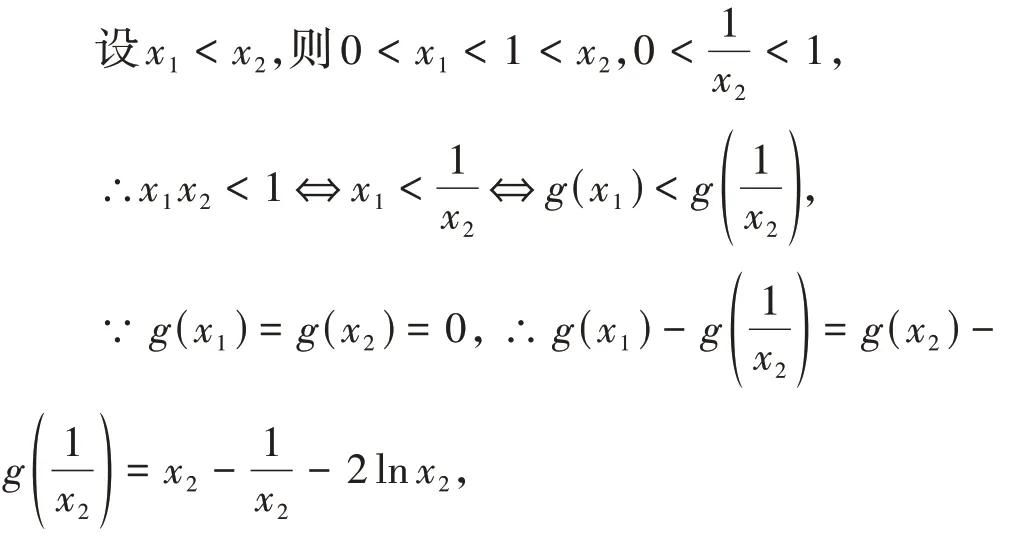
三、比值換元

運用比值換元法解決極值點偏移證明問題，關鍵在于用兩極值點之比替換問題中的變量x1，x2。解題時通常把極值點之比看作新變量t，把問題轉化成關于t的函數問題，進而對有關t的函數進行分析，解決問題。具體解題步驟如例3所示。

［例3］已知函數f(x)=ex-ax有兩個零點分別為x1，x2，若a∈(e,+∞)，求證：x1+x2＞2。

分析：首先作差把函數f(x)=ex-ax兩個零點對應等式中的參數消去，可得=ax2；其次根據得到的式子找到x1與x2之間的聯系，不難得到x2-x1=lnx2-lnx1；最后引入新變量t=，把證明x1+x2＞2 轉化為關于t的函數問題，對函數h(t)=lnt-進行探究。

證明：由f(x)=ex-ax，得f′(x)=ex-a，

∵a∈(e,+∞)，∴f(x)在(0,1)和(1,3a)上各有一個零點，

設0 ＜x1＜x2，

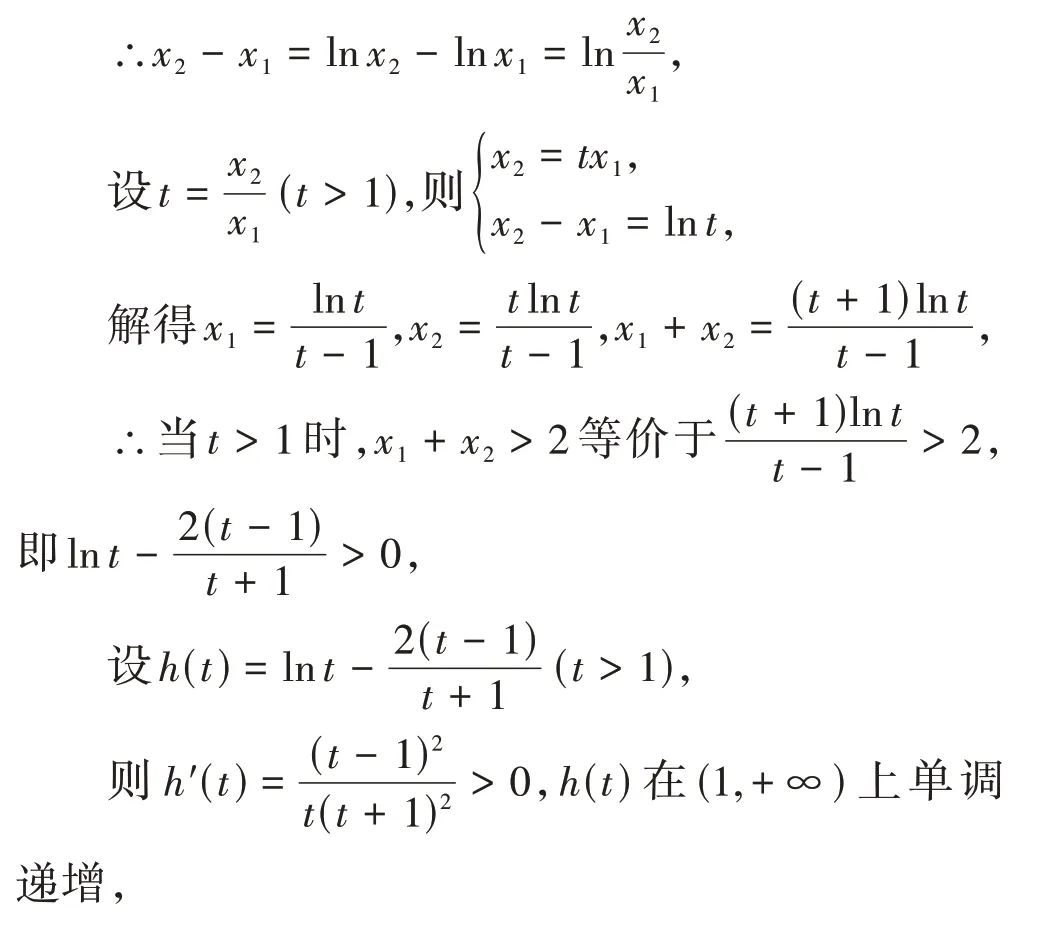
∴h(t) ＞h(1)=0，即lnt-

∴x1+x2＞2。

評析：通過上述問題及解題過程，不難發現通過x2-x1=lnx2-lnx1引入變量t=是解題的關鍵，也是解題的難點所在。運用比值換元法解題，最終也是消去參數，減少變量個數，與其他方法殊途同歸，都使問題更加直觀簡潔。

四、利用單調性

利用單調性解決極值點偏移證明問題，著重于用“當導函數f′(x) ＞0 時函數f(x)單調遞增”和“當f′(x) ＜0 時函數f(x)單調遞減”來將自變量的大小關系轉變為函數的大小關系。解題時通常利用上述轉化而來的函數大小關系構造新的函數，進而求解新函數的導數，確定新函數的單調性及其在取值范圍內的最大值或最小值。具體解題步驟如例4所示。

［例4］已知函數f(x)=xe-x（x∈R），如果x1≠x2，且有f(x1)=f(x2)，證明：x1+x2＞2。

分析：因為f′(x)=所以當x＜1 時有f′(x) ＞0，函數f(x)=xe-x單調遞增；當x＞1 時有f′(x) ＜0，函數f(x)=xe-x單調遞減。要證明x1+x2＞2，即證明x2＜2-x1，直接令x1＜1 ＜x2，得到2-x1＞1，此時x2和2-x1都在函數f(x)的單調遞減區間中，因此只需要證明f(x2)＜f(2-x1)即可。根據已知條件f(x1)=f(x2)可知，只需要證明f(x1)＜f(2-x1)，通過構造函數F(x)=f(x)-f(2-x)(x＜1)，F′(x)=f′(x)-f′(2-x)=(1-e2x-2)，再分析當x＜1時對應的F(x)的導函數F′(x)的情況，即可得到f(x1)＜f(2-x1)，由此證明x1+x2＞2。

證明：已知函數f(x)=xe-x，則其導函數為f′(x)=當x＜1 時有f′(x) ＞0，函數f(x)單調遞增；當x＞1 時有f′(x) ＜0，函數f(x)單調遞減。要想證明x1+x2＞2，即證明x2＜2-x1，所以直接假設x1＜1 ＜x2，即2-x1＞1，此時x2和2-x1都在函數f(x)的單調遞減區間中，所以只需要證明f(x2)＜f(2-x1)。

∵f(x1)=f(x2)，

∴只需證明f(x1)＜f(2-x1)即可，

令F(x)=f(x)-f(2-x)(x＜1)，

則F′(x)=f′(x)-f′(2-x)=

∵x＜1，

∴2x-2 ＜0，等價于e2x-2＜1，

∴F′(x) ＞0，

因此，當x＜1時，函數F(x)單調遞增，

又∵F(1)=0，

∴f(x) ＜f(2-x)(x＜1)，即f(x1)＜f(2-x1)，

即證x1+x2＞2成立。

評析：求解這類問題，首先分析原函數的單調性，然后進行合理分析并反推，將自變量的大小關系用函數的大小關系表示出來，再根據得到的函數大小關系構造新的函數，最后對新函數進行求導，利用新函數的單調性及其在取值范圍內的最大值或最小值求證即可。

綜上可知，對稱變換、消參減元、比值換元以及利用單調性等方法都能夠有效解決極值點偏移證明問題。在教學中，教學應善于引導學生發現試題的命題規律，熟悉并掌握解答問題的方法，從而提升學生的解題效率和解題能力，培養學生的數學學科核心素養。