基于神經網絡算法的發射場坪承載能力預測方法

勵明君， 姜毅， 馬立琦， 潘霄

(北京理工大學 宇航學院， 北京 100081)

0 引言

導彈機動發射可以在不同陣地之間快速機動，且轉移路線靈活多變，是未來陸基導彈武器的重點發展方向之一。為保證導彈發射的安全性，同時提高戰時快速機動和快速響應能力，在發射前對場坪的承載能力進行快速預測，確保發射場坪在發射階段能夠提供穩定持續的支撐能力，具有重要的戰略意義。

發射過程中，支腿在起豎和發射階段對發射場坪均有不可忽視的沖擊效應。國內外學者對此進行了廣泛研究。姚曉光等基于轉動運動函數和轉動微分方程，建立了起豎機構在導彈起豎過程中的力學模型并通過仿真分析進行了驗證。周曉和等以導彈發射場坪為研究對象，建立了其塑性損傷動態本構，發現在導彈發射階段場坪于發射筒底部處有沉降最大響應；Ren等使用Drucker-Prager/Creep蠕變模型對混凝土發射場坪進行彈塑性分析，結果表明場坪在發射載荷作用中心點具有最大位移響應。發射場坪是包含面層、基層、底基層和土基層的復雜層狀體系，結構層的厚度、彈性模量、泊松比和材料的種類、溫度、含水量等均成為影響發射場坪承載能力的重要因素。程洪杰等提出了一種發射場坪承載強度的判斷方法，以支腿對地最大載荷狀態作為強度評估的重要依據，并在發射場坪承載力計算模式的基礎上分析了內聚力、內摩擦角、覆層厚度等多種影響因素的敏感性。袁成林圍繞某型冷發射裝備，對多種典型公路結構進行歸納分析，構建發射場坪動力學模型，研究了對路面動力學響應特性影響較大的影響因子的發展規律。

目前，發射場坪的動力學響應研究方法主要為顯示動態計算。然而，戰時狀態下，發射場坪的選擇具有隨機性和未知性，相關結構參數以及特種車輛在不同狀態下的對地載荷難以預測。同時，發射場坪的仿真模型建模難度大，耗費時間長。因此，在滿足精度和可靠性的前提下，為保證發射方式的快速響應和快速反擊能力，有必要在發射前對場坪的支撐強度進行快速準確預測，縮短準備時間。當前，深度學習技術飛速發展，被應用在不同領域，有效解決了許多難題。國內外學者利用機器學習技術建立了近似模型，重點關注對已知發射場坪承載能力的影響因素進行敏感度評估，但是在對未知參數的發射場坪承載能力預測方面存在一定的局限性。

本文引入發射場坪參數敏感度對拉丁超立方試驗設計方法進行優化，構建更好地描述樣本特征的數據集，節省計算資源；使用3種不同的神經網絡回歸預測算法，分別按照圖1所示流程圖建立發射場坪承載能力預測近似模型，并通過誤差分析、方差分析和殘差分析分別對比討論了近似模型在起豎和發射載荷下的優劣；提出一種根據含未知結構參數的發射場坪在起豎載荷下的動力學響應，預測該場坪在發射載荷下承載能力的預測算法，并對預測算法在測試數據集的表現進行分析，驗證了其有效性。

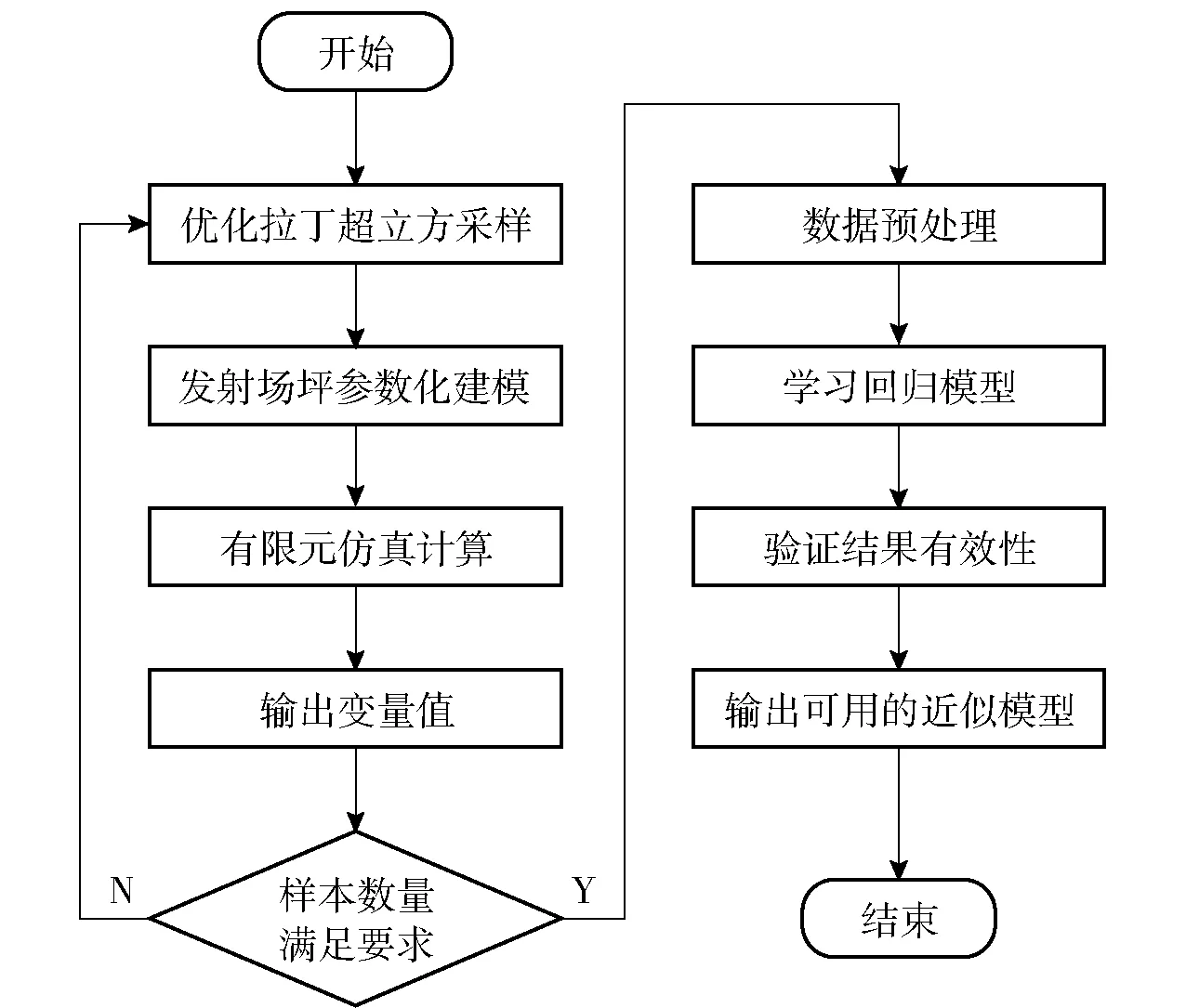
圖1 近似模型建立過程流程Fig.1 Flow chart of establishing an approximate model

1 發射場坪承載特性近似模型

以典型剛性混凝土發射場坪為研究對象，將其看作從上至下依次由面層、基層、底基層和土基組成的層狀體系并進行一定簡化。假設各層結構均完整、均勻、連續，考慮面層混凝土損傷塑性模型和土基的破壞模型；各結構層之間完全連續。將圓形支腿以及發射筒底座均看作剛體，對場坪的載荷假定為圓形均勻垂直分布。本文重點關注場坪在起豎和發射載荷下的法向位移，典型場坪結構及相關材料如圖2所示。圖2中，為坐標原點，為典型場坪結構切面的極坐標系，、、分別為混凝土面層、基層和底基層的厚度，、、、分別為混凝土面層、基層、底基層、土基層的彈性模量，、、、分別為混凝土面層、基層、底基層、土基層的泊松比，()為作用在場坪表面的圓形均布載荷。

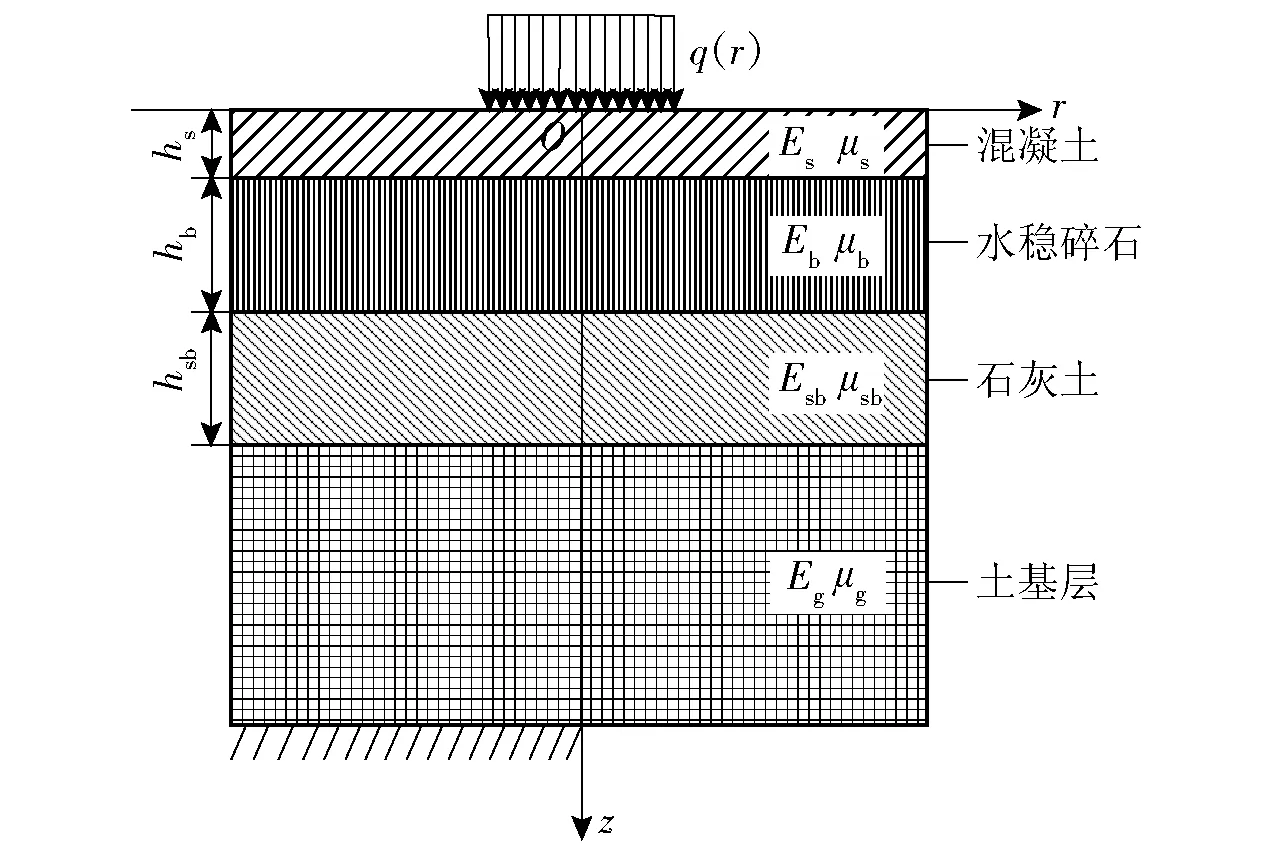
圖2 典型場坪結構示意圖Fig.2 Structural diagram of typical launching site

1.1 優化拉丁超立方采樣

近似模型的訓練數據特征參數包括面層厚度和彈性模量、基層厚度和彈性模量、底基層彈性模量、土基彈性模量等。根據現有的研究結果可知，不同結構參數對場坪承載能力的影響敏感度不同，相同結構參數在不同取值范圍內敏感度也各異。其中，面層厚度和土基彈性模量的影響最大，總體趨勢為取值越小，敏感度越小。拉丁超立方采樣方法根據樣本個數將累計概率分布曲線均勻分層，每層隨機抽取一個值作為樣本，抽樣不替換，導致當采樣點個數相同時，在敏感度小的參數取值區間內描述性好，而在敏感度大的參數取值區間內描述性差。因此對上述采樣方法進行優化，對參數所在值域區間的敏感度曲線()，從取值下限到取值上限進行積分，積分值記為，如(1)式：

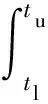
(1)

設樣本分層層數為，對任意分層區間[,+1]，=1,2,…,,使其滿足

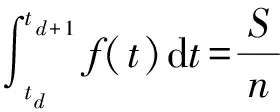
(2)

事實上，=，=，利用牛頓- 萊布尼茨公式對(=2,3,…,-1)依次求解，即可得到考慮參數敏感度的非均勻分層區間，并在區間內隨機抽取一個樣本。此優化方法使分層在敏感度大的區域密集，在敏感度小的區域稀疏。圖3為考慮某參數敏感度曲線的分層策略示意圖。

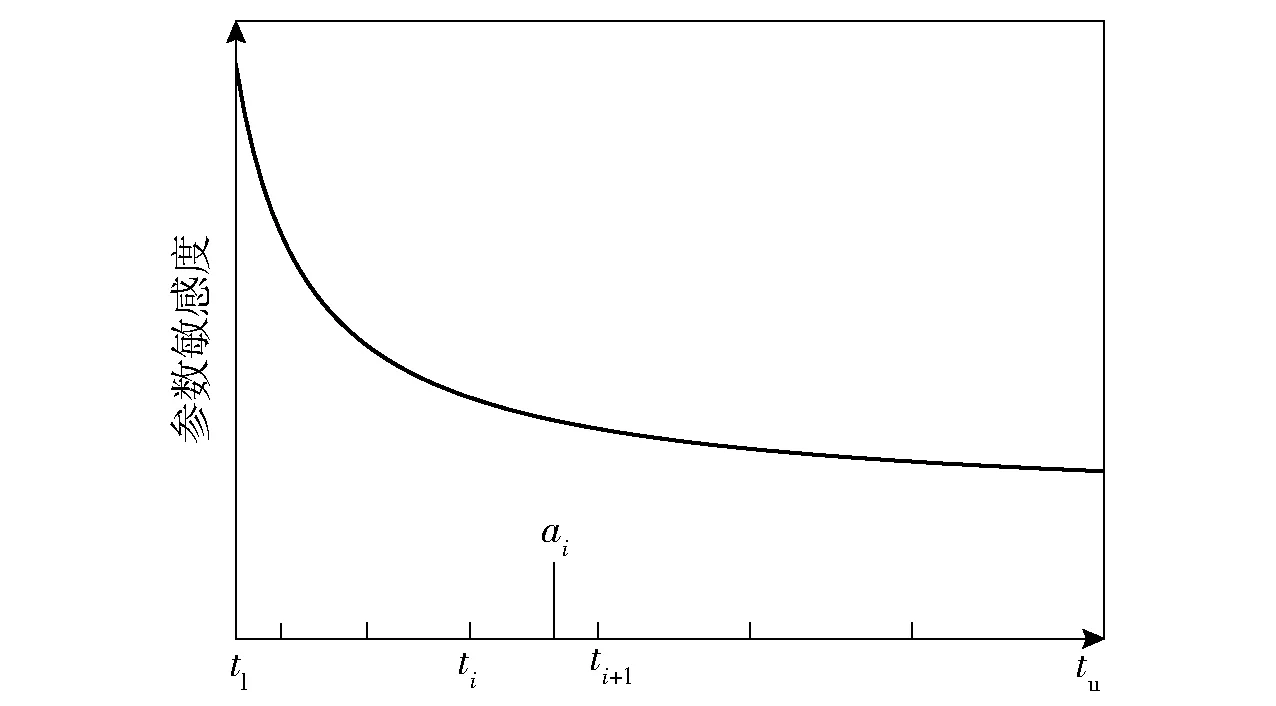
圖3 考慮參數敏感度分層Fig.3 Stratification considering parameter sensitivity

以面層厚度和土基彈性模量為例，假設面層厚度和土基彈性模量的取值區間均為[0 MPa，150 MPa]，樣本數量為30，分別使用經典拉丁超立方試驗方法和優化拉丁超立方試驗方法進行采樣，結果如圖4、圖5所示。從圖4、圖5中可以看出，經典拉丁超立方采樣點具有更優的均勻性，但基于參數敏感度曲線的優化拉丁超立方采樣在面層厚度和土基彈性模量較小的區域內采樣更為密集，能夠更好地描述輸入數據在特征空間的分布。

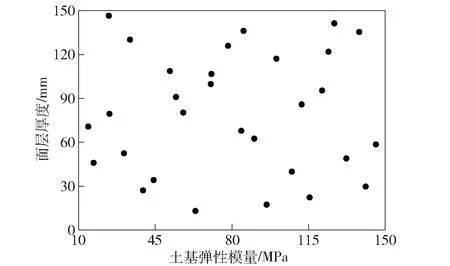
圖4 經典拉丁超立方采樣示意圖Fig.4 Classical Latin hypercube sampling

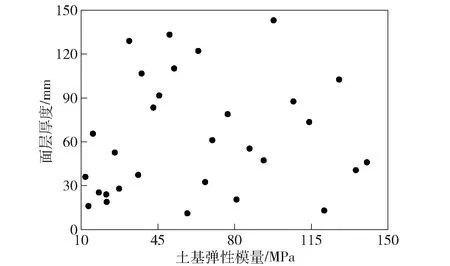
圖5 優化拉丁超立方采樣示意圖Fig.5 Optimized Latin hypercube sampling

1.2 有限元數值模型

分別建立發射場坪在起豎和發射載荷下的有限元模型，并根據優化拉丁超立方采樣結果進行參數化計算。

1.2.1 勻速起豎過程場坪受力曲線

根據文獻[11]，起豎油缸對發射筒的推力僅與發射箱的起豎規律()有關。本文以勻速起豎為例，計算得到無量綱化前、后支腿對場坪表面的支承力隨起豎角度的變化曲線，如圖6所示。

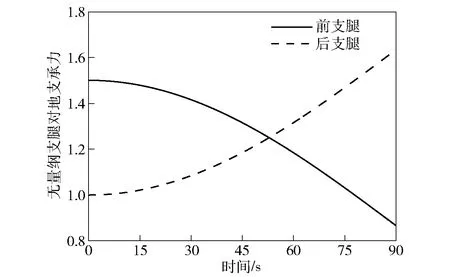
圖6 前、后支腿對地支承力隨起豎角度變化曲線Fig.6 Curves of the supporting forces of front and rear supporting plates changing with the hoisting angle

1.2.2 發射過程場坪受力曲線

本文重點關注發射狀態時，發射筒底座處場坪的最大彎沉值，忽略支腿與發射筒底部之間的相互影響。

圖7為某彈射裝置對發射場坪的沖擊力變化示意圖。圖7中為發射時間，為沖擊力，為沖擊力在發射過程中的最大值。

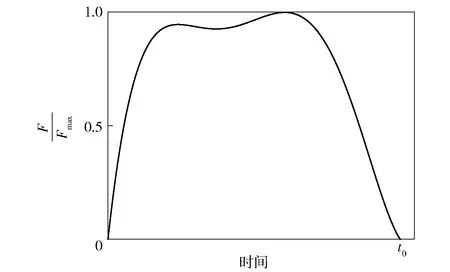
圖7 某發射裝置的沖擊力曲線Fig.7 Impact force curve of ejection device

1.2.3 場坪有限元數值模型

以某典型場坪為研究對象，考慮瀝青混凝土的材料非線性，引入塑性損傷模型，其膨脹角為30°，偏心率為0.1，并采用基于高斯積分方法的經典損傷理論法求解混凝土受壓和受拉損傷因子，在無可靠試驗驗證的情況下，該求解方法是可用于計算的。同時考慮土基的Drucker Prager破壞模型，內摩擦角為25°，膨脹角為20°，屈服應力比為0.95。其余各層材料以線彈性本構關系處理，建立發射場坪的有限元仿真模型。在建模過程中，忽略溫度、含水量和結構孔隙對材料特性的影響；相鄰結構層之間完全接觸，力學特性連續；距離載荷作用中心足夠遠處的應力為0 MPa，應變均0；考慮場坪各結構層的初始地應力，忽略加載時前后支腿與發射筒底座的相互影響。仿真計算的初始時刻，場坪處于考慮自重的應力平衡狀態。

建模過程中發射車支腿對地載荷為半徑0.5 m的圓形載荷，發射筒底座對地載荷為半徑0.9 m的圓形載荷，場坪尺寸為12 m×12 m×18 m。為減少計算量，考慮到發射場坪結構和激勵載荷均為軸對稱，建立場坪的四分之一有限元仿真模型。模型的約束為：對稱面約束法向平移運動及繞軸、軸的轉動，對稱面約束法向平移運動及繞軸、軸的轉動，其余兩個側面設置自由約束，土基底面設置固定端約束。場坪有限元仿真模型如圖8所示。

圖8 發射場坪有限元仿真模型Fig.8 Finite element simulation model of launching site

1.2.4 神經網絡算法近似模型

采用3種不同的神經網絡算法模型，分別是線性多元回歸模型、反向傳播(BP)神經網絡模型和徑向基函數(RBF)神經網絡模型，將場坪結構參數取樣結果作為特征輸入，以場坪在對應載荷下的最大彎沉值為輸出，基于樣本集的迭代計算得到各模型的回歸系數或連接權值等參數，最終建立發射場坪承載能力快速評估的近似模型。

1.2.5 線性多元回歸模型

本文在研究過程中發現，部分參數如面層厚度、基層厚度等對場坪彎沉值的影響趨于線性規律。假定特征參數的影響程度相互獨立，考慮利用線性多元回歸模型。

線性多元回歸模型中預測變量與特征參數之間的函數關系為

=++…++…++

(3)

式中：為樣本總量；為預測變量；為樣本真實值；為偏回歸系數；為誤差項。本文中由場坪各結構層參數和對應的場坪下沉量最大值組成樣本空間，通過最小二乘法進行參數估計，得到和的具體值，建立場坪承載能力的線性多元回歸模型。

126 BP神經網絡模型

BP神經網絡模型包含輸入層、中間隱含層和輸出層。圖9給出了一個由個輸入神經元、個輸出神經元以及個隱層神經元組成的多層前饋網絡結構拓撲圖。設為第個樣本的真實輸出值，給定訓練集={(,),(,),…,(,)},∈，∈，即輸入參數由個屬性描述，輸出維實值向量。隱含層包含個神經元，為第(=1,2,…,)個輸入層神經元和第(=1,2,…,)個隱含層神經元之間的連接權值，為第個隱含層神經元與第(=1,2,…,)個輸出層神經元之間的連接權值，為第個隱含層神經元的輸出值。模型訓練前對連接權值進行隨機初始化，在迭代過程中采用廣義的感知學習規則對參數在每一輪中進行更新估計。任意參數的更新估計式為

←+Δ

(4)

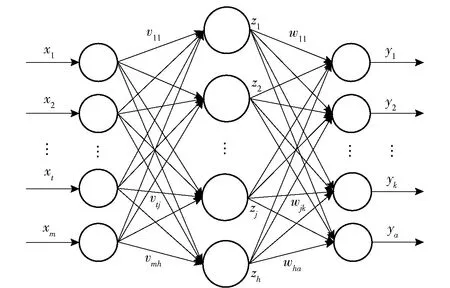
圖9 BP神經網絡結構拓撲圖Fig.9 Topology graph of back propagation neural networks

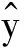
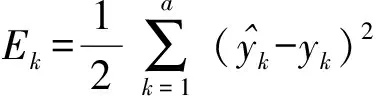
(5)

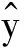
通過誤差Δ的反向傳播，根據(4)式對權值及閾值參數進行迭代。Δ與學習率、激活函數的性質以及上一輪迭代的均方誤差有關。

本文建立了含3層隱含層的BP神經網絡近似模型，神經元個數分別為20、40和30。學習率的初始值設定為0001，采用ReLU激活函數。Adam算法的參數設置：=09,=0999,=10，其中，為一次估計指數衰減率，為二次估計指數衰減率，參數防止算法運行過程中出現0。

127 RBF神經網絡模型

RBF神經網絡是一種單隱層前饋神經網絡。當隱層神經元足夠多時，RBF神經網絡能以任意精度逼近任意連續函數。它的隱層神經元激活函數為沿徑向對稱的標量函數，即RBF。輸出層是對隱層神經元的線性組合。設輸入為維向量，輸出為實值，則RBF神經網絡可表示為

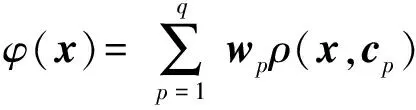
(6)

式中：為隱層神經元個數；和分別為第個隱層神經元對應的中心和權重；(,)為樣本到數據中心之間歐氏距離的單調函數。本文所用的高斯RBF函數如(7)式所示，算法內核類型為RBF。

(,)=e-‖-‖

(7)

128 發射場坪近似模型的建立

根據圖1，將場坪每個結構層的厚度、彈性模量和泊松比均作為輸入參數，根據表1中各參數的取值范圍及敏感度曲線，應用優化拉丁超立方試驗設計方法采樣，隨機設定220種場坪結構。通過有限元仿真計算，得到對應工況載荷作用中心處的最大彎沉值，與場坪結構層的的力學參數共同構建訓練數據集。利用上述3種回歸算法進行迭代優化，建立發射場坪承載特性近似模型，預測某未知場坪在相應載荷下的最大彎沉值。

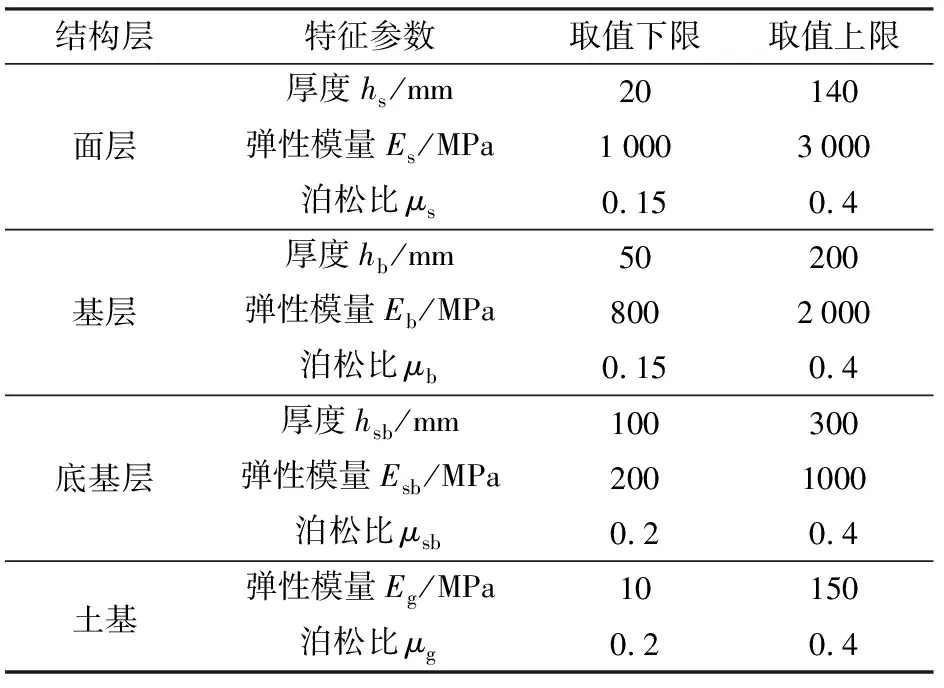
表1 特征參數及變量范圍Tab.1 Feature parameters and variable scope

2 預測算法有效性分析

在學習回歸模型前，需要對訓練集數據通過(8)式進行歸一化預處理。

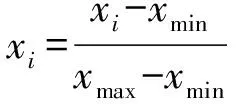
(8)

式中：和分別為訓練集中參數的最大值和最小值。

2.1 起豎載荷下預測算法的有效性

采用優化拉丁超立方試驗設計方法，在表2所示取值區間內隨機抽樣，構建起豎載荷下場坪承載能力近似模型的220個數據集，樣本空間如表2所示，其中包括訓練集和測試集，測試集隨機抽取17個樣本且不參與訓練過程。

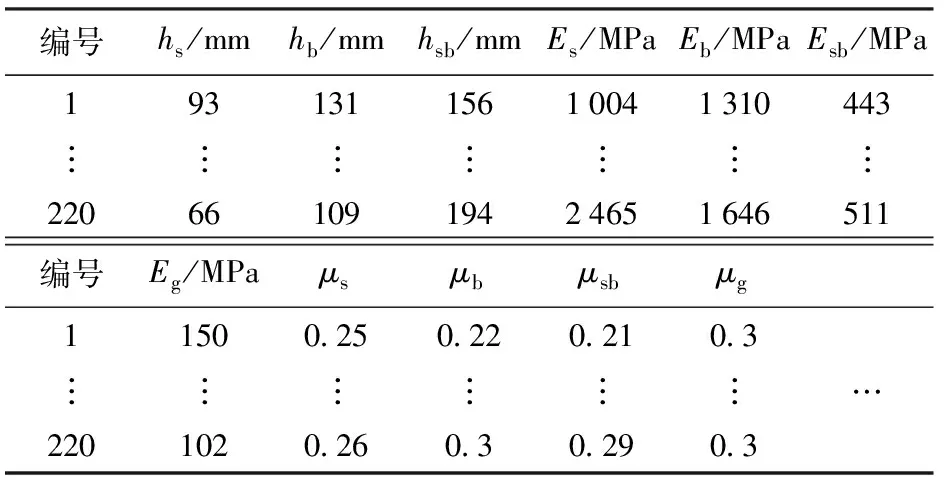
表2 起豎載荷下近似模型樣本空間Tab.2 Sample space table of approximate model undererection load

采用1.3節中的3種神經網絡模型分別得到測試集輸入條件下場坪彎沉量的預測值，與有限元仿真值進行對比分析。通過數據對比可以得到：線性多元回歸模型預測結果的誤差大部分集中在10%～20%之間，最大誤差36.85%，最小誤差0.63%；BP神經網絡模型預測結果的最大誤差為33.4%，最小誤差2.29%；RBF神經網絡模型預測結果的誤差大部分在10%以內，最大誤差28.8%，最小誤差0.16%。

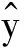
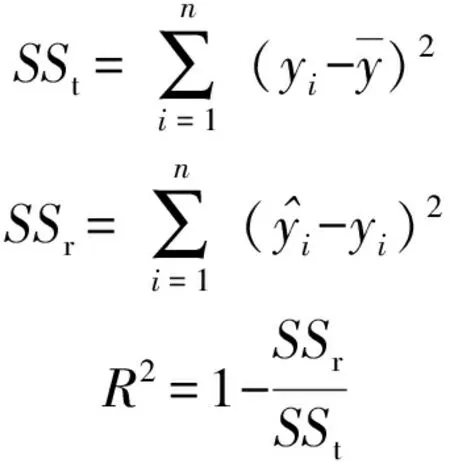
(9)

式中：為真實值離均差平方和；為預測值離均差平方和；表征近似模型的擬合精確度，取值范圍為(0,1)，其值越接近1，表明近似模型的預測值準確度越高。

圖10、圖11、圖12分別為起豎載荷下3種預測模型對測試集的預測結果與相應的有限元算法仿真值的方差分析對比圖。縱向對比發現，RBF神經網絡模型的值最大(0.941)，模型精度最高。線性多元回歸模型和BP神經網絡模型分別為0.748和0.762，模型精度不理想。BP神經網絡模型預測結果較差的原因可能是樣本數量不足，難以充分發揮多隱層神經網絡算法的潛力。

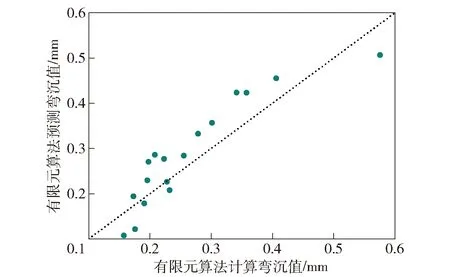
圖10 線性多元回歸模型方差分析(R2=0.748)Fig.10 Variance analysis of linear multiple regression model(R2=0.748)

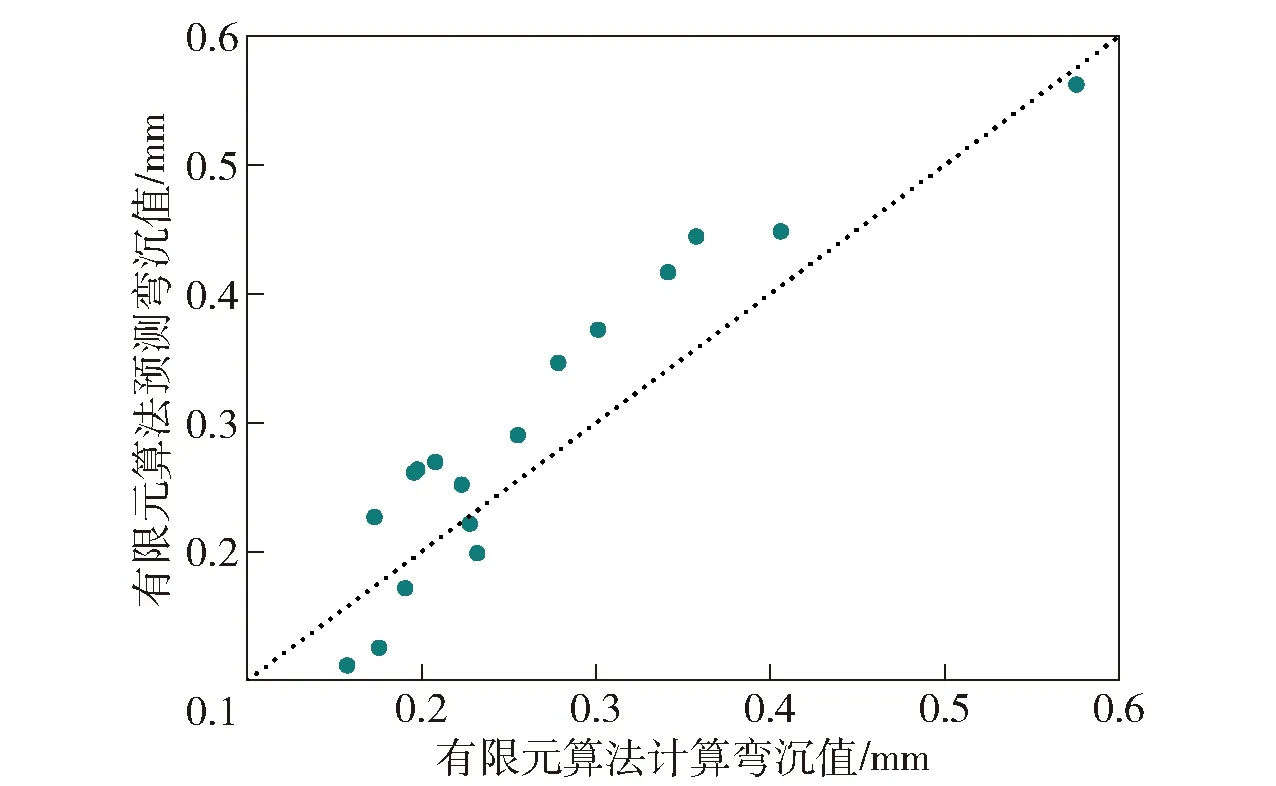
圖11 BP神經網絡模型方差分析(R2=0.762)Fig.11 Variance analysis of BP neural networks model (R2=0.762)

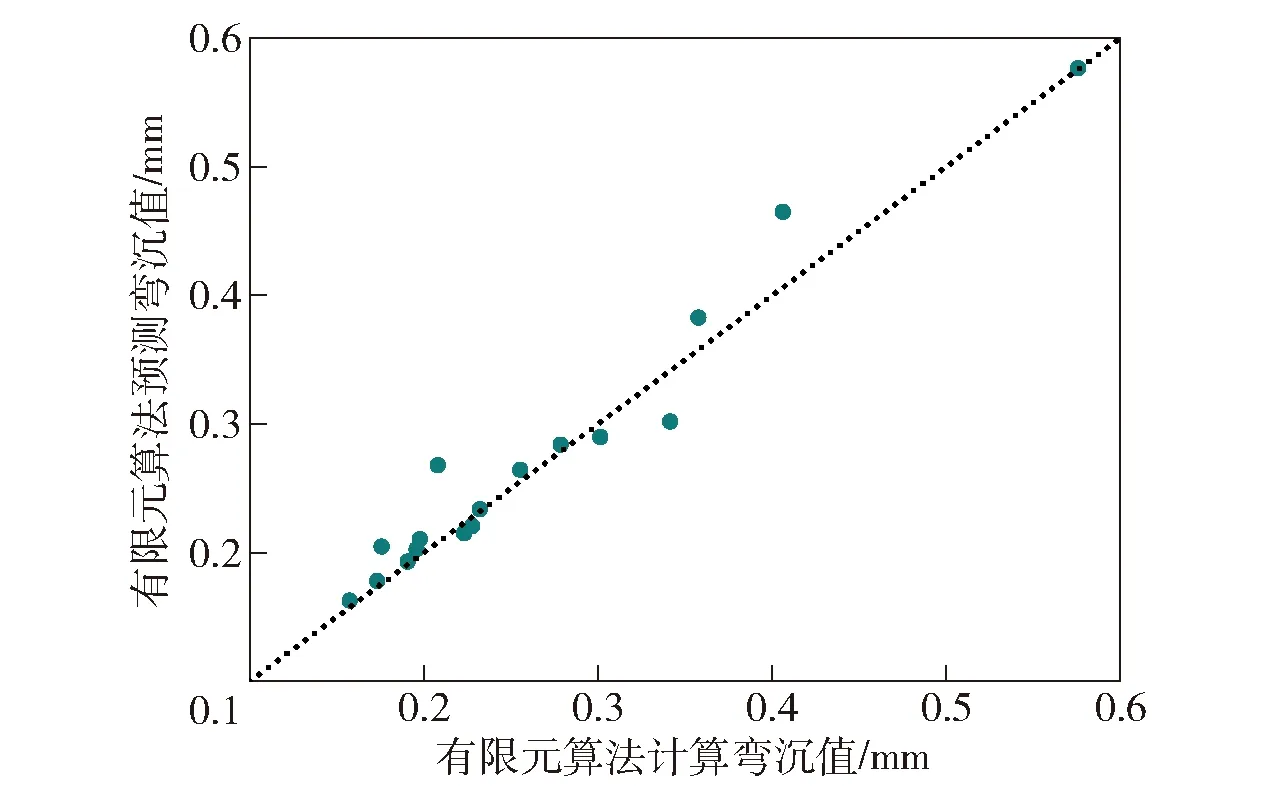
圖12 RBF神經網絡模型方差分析(R2=0.941)Fig.12 Variance analysis of RBF neural networks model (R2=0.941)

圖13、圖14、圖15分別為3種預測模型對測試集的預測結果與相應的有限元仿真值的殘差分析圖。對比發現3種模型預測結果的殘差都在0.1 mm范圍內。RBF神經網絡模型的殘差值普遍較另外兩種模型小，最大僅為0.059 9 mm。

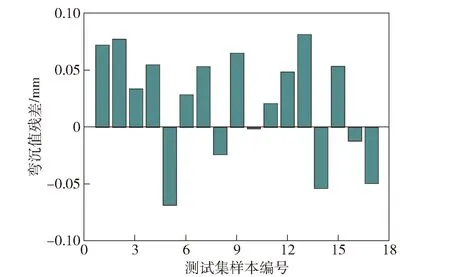
圖13 線性多元回歸模型殘差分析Fig.13 Residual analysis of linear multiple regression model

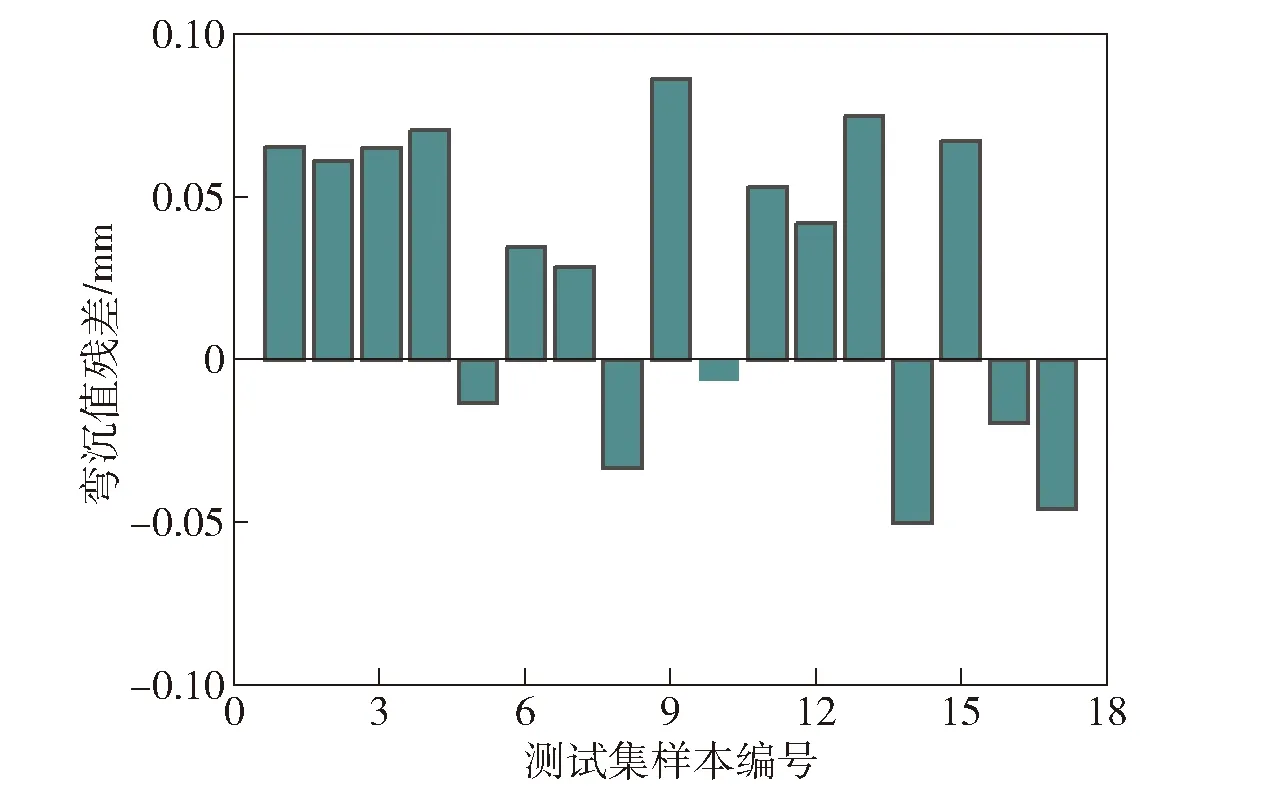
圖14 BP神經網絡模型殘差分析Fig.14 Residual analysis of BP neural networks model

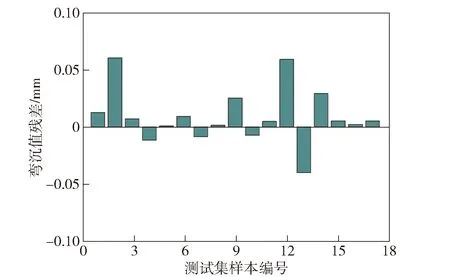
圖15 RBF神經網絡模型殘差分析Fig.15 Residual analysis of RBF neural networks model

上述3種預測模型的單個工況平均計算時間分別為3.1 s、2.0 s和40.6 s。RBF神經網絡結構較為復雜，因此計算時間相對于前二者更長。然而，起豎載荷下單次有限元仿真計算所需平均時長約為44.2 min。采用神經網絡預測模型耗費的計算時長和資源大大減少。

綜合上述分析結果可知，當樣本數有限時，RBF神經網絡模型對場坪在起豎載荷下的彎沉值預測具有最優能力，可以在一定程度上代替有限元仿真方法進行工程化應用。

2.2 發射載荷下預測算法的有效性

同樣采用優化拉丁超立方試驗設計方法，在取值區間內隨機抽樣構建發射載荷下場坪承載能力近似模型的樣本空間，如表3所示。

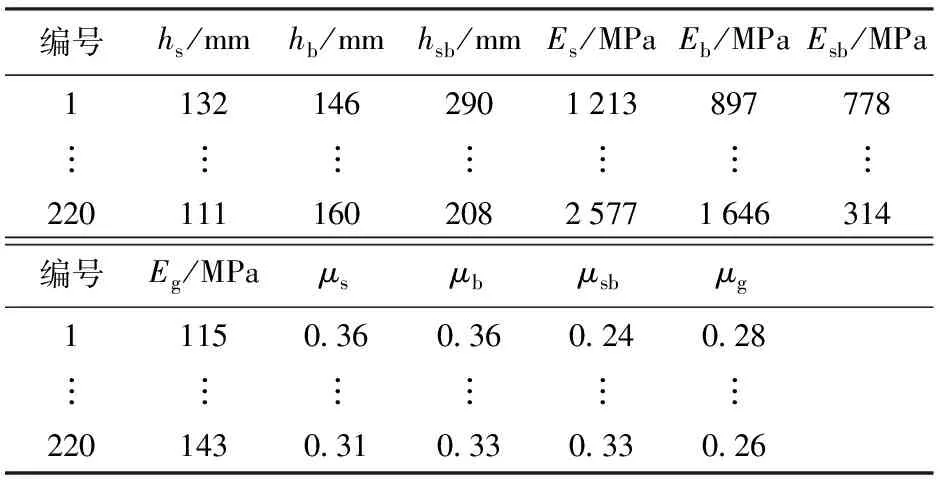
表3 發射載荷下近似模型樣本空間Tab.3 Sample space table of approximate modelunder launch load

將樣本空間數據集劃分為訓練集和測試集，測試集包含14個樣本。分別使用線性多元回歸模型、BP神經網絡模型和RBF神經網絡模型對訓練集進行機器學習后，得到測試集的預測結果。對預測結果和有限元仿真結果進行誤差分析，可以發現：線性多元回歸模型的預測值最大誤差38.76%，最小誤差1.75%；當場坪承載能力較強、彎沉幅度較小時，預測誤差在10%以內，近似模型表現良好；對于彎沉值大于25 mm的場坪結構，預測性能比較不理想；BP神經網絡模型預測結果最大誤差46.66%，最小誤差4.13%；對彎沉值超過25 mm的場坪結構同樣具有不可預測性，在低強度場坪的平均誤差較高，可能是由于BP神經網絡模型在迭代過程中參數較多，需要具有數量龐大的樣本集才能保證足夠的精確度，否則會造成欠擬合現象；RBF神經網絡模型最大誤差13.55，最小誤差0.37%，在全值域空間內誤差普遍偏小，具有良好的回歸預測性能。

圖16、圖17、圖18分別為發射載荷下3種模型對場坪彎沉的預測值與有限元仿真值的方差分析圖。縱向對比可以發現：RBF神經網絡模型的值最大(0.983)，表明線性回歸擬合度高，方差小，精度高，近似模型的可靠性強；相比之下，線性多元回歸模型和BP神經網絡模型值分別為0.633和0.775，結果擬合度不理想，分析其原因可能是對弱強度場坪的預測性能較差，導致誤差較大。

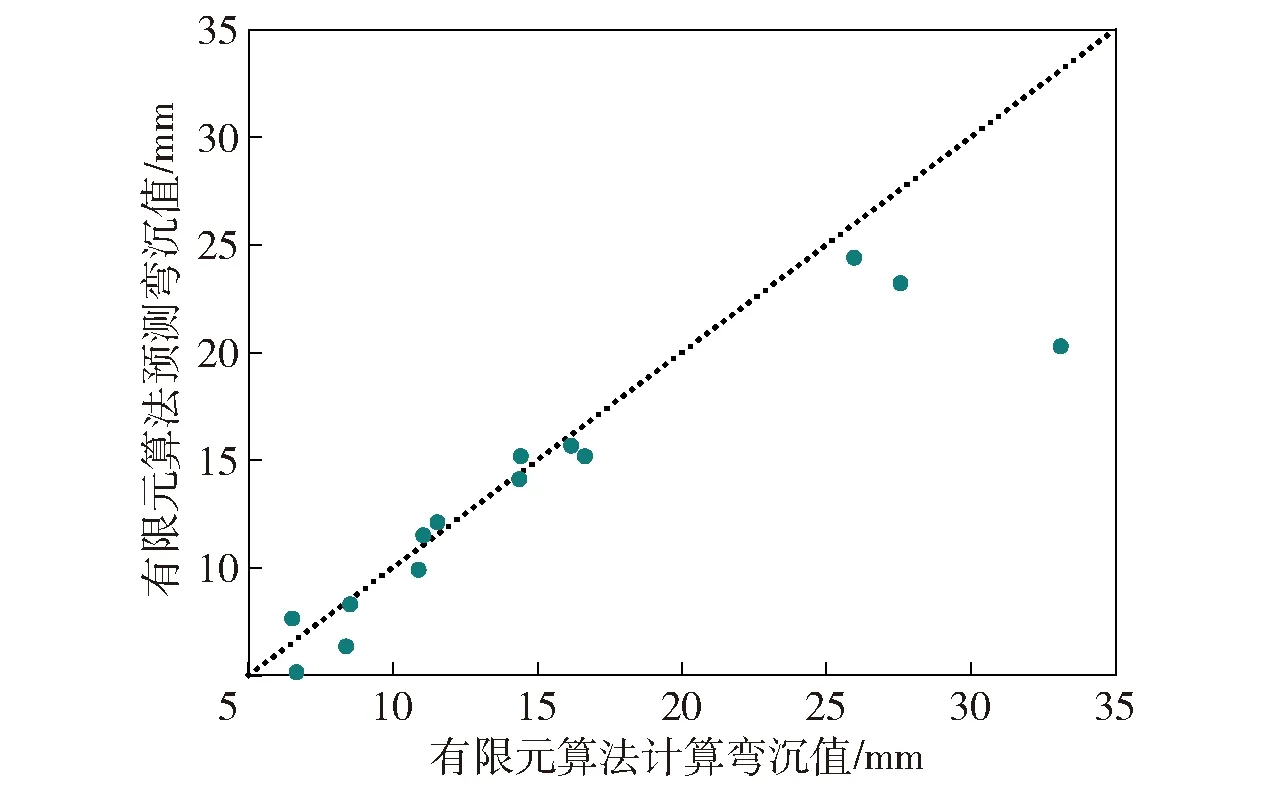
圖16 線性多元回歸模型方差分析(R2=0.633)Fig.16 Variance analysis of linear multiple regression model (R2=0.633)

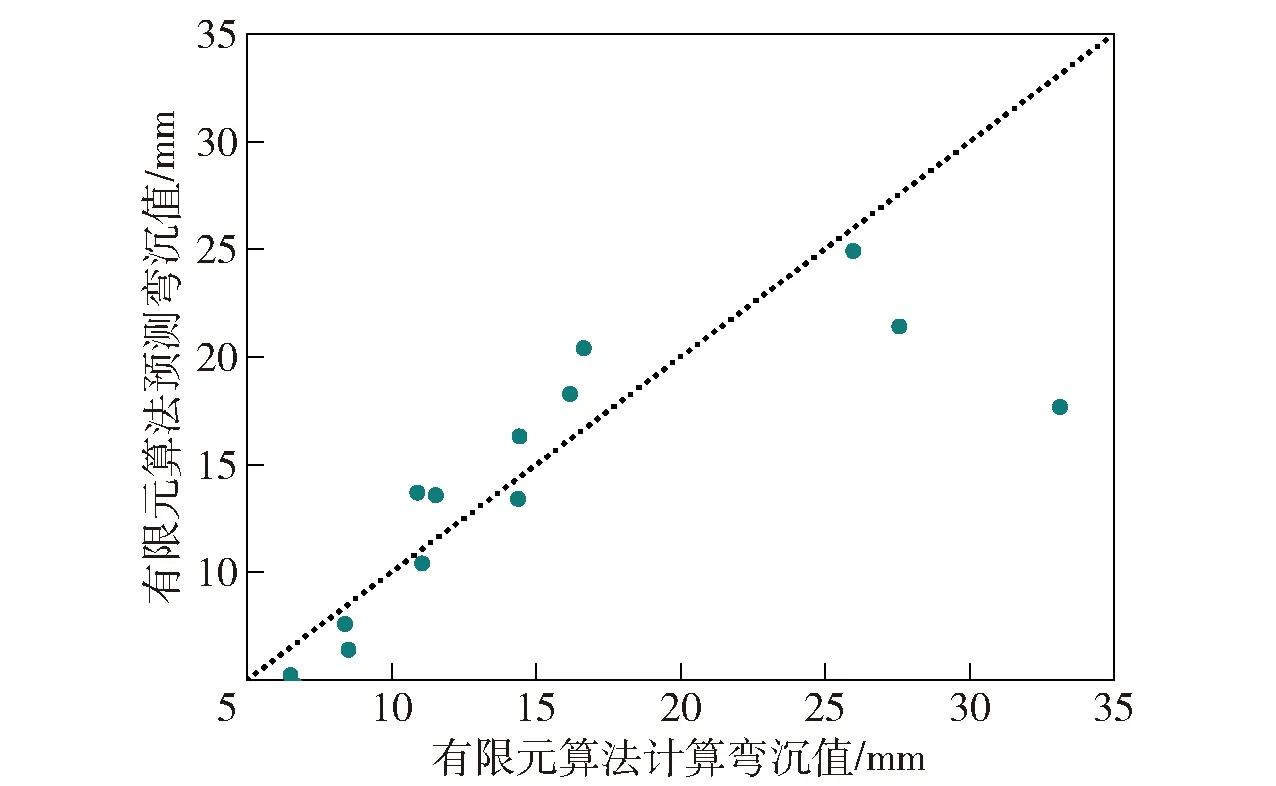
圖17 BP神經網絡模型方差分析(R2=0.775)Fig.17 Variance analysis of BP neural networks model(R2=0.775)

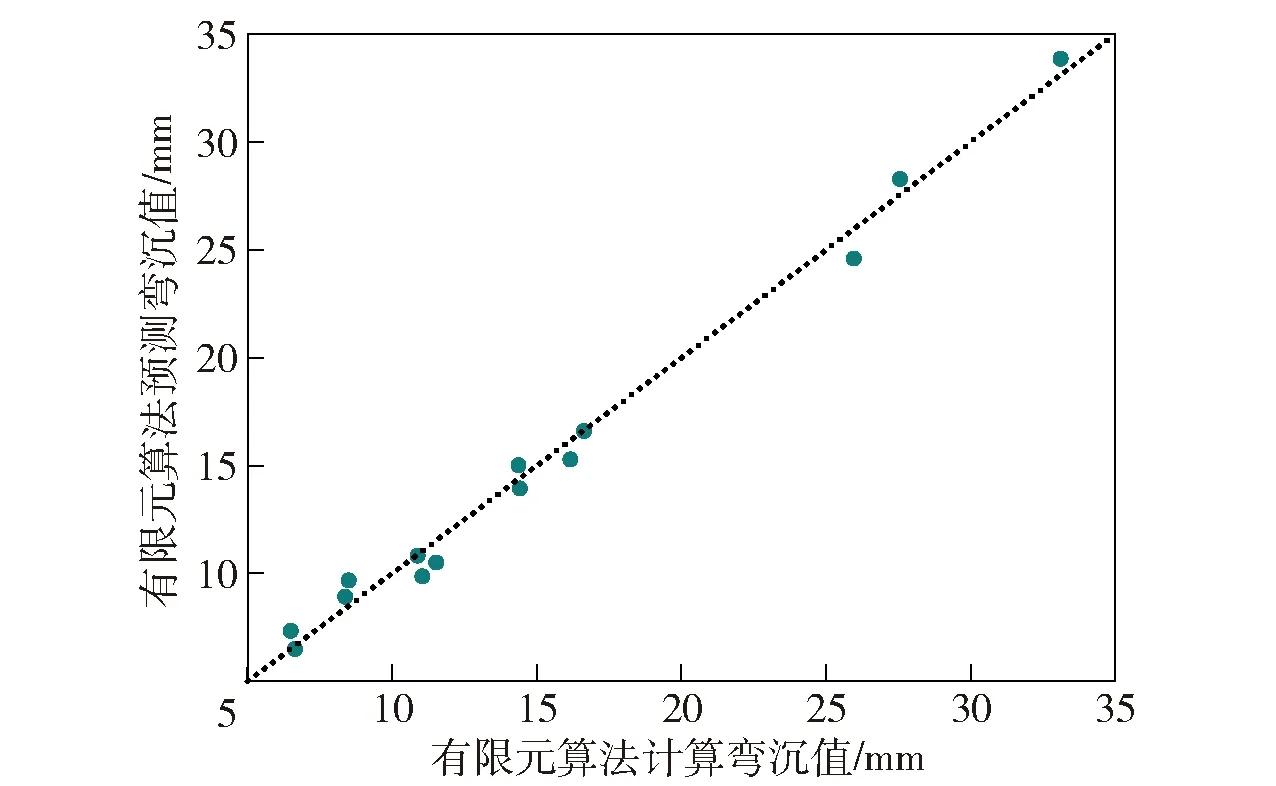
圖18 RBF神經網絡模型方差分析(R2=0.983)Fig.18 Variance analysis of RBF neural networks model (R2=0.983)

圖19、圖20、圖21分別為不同近似模型下場坪彎沉值的預測值與仿真值的殘差分析圖。縱向對比可以看出：線性多元回歸模型和BP神經網絡模型的殘差范圍大部分都在±4 mm以內，但有部分較大異常值，使得預測結果偶爾會出現較大誤差；RBF神經網絡模型的殘差均在±1.5 mm范圍內，預測性能明顯優于前二者。

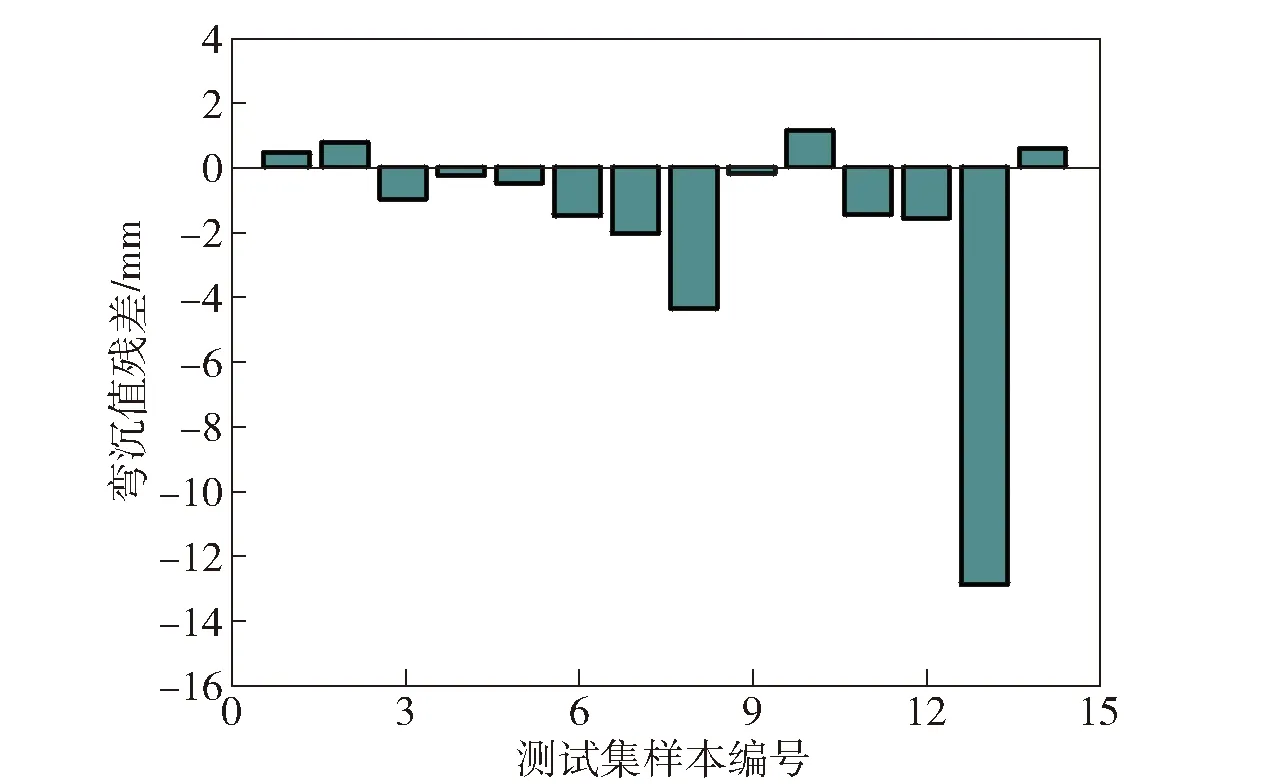
圖19 線性多元回歸模型殘差分析Fig.19 Residual analysis of linear multiple regression model

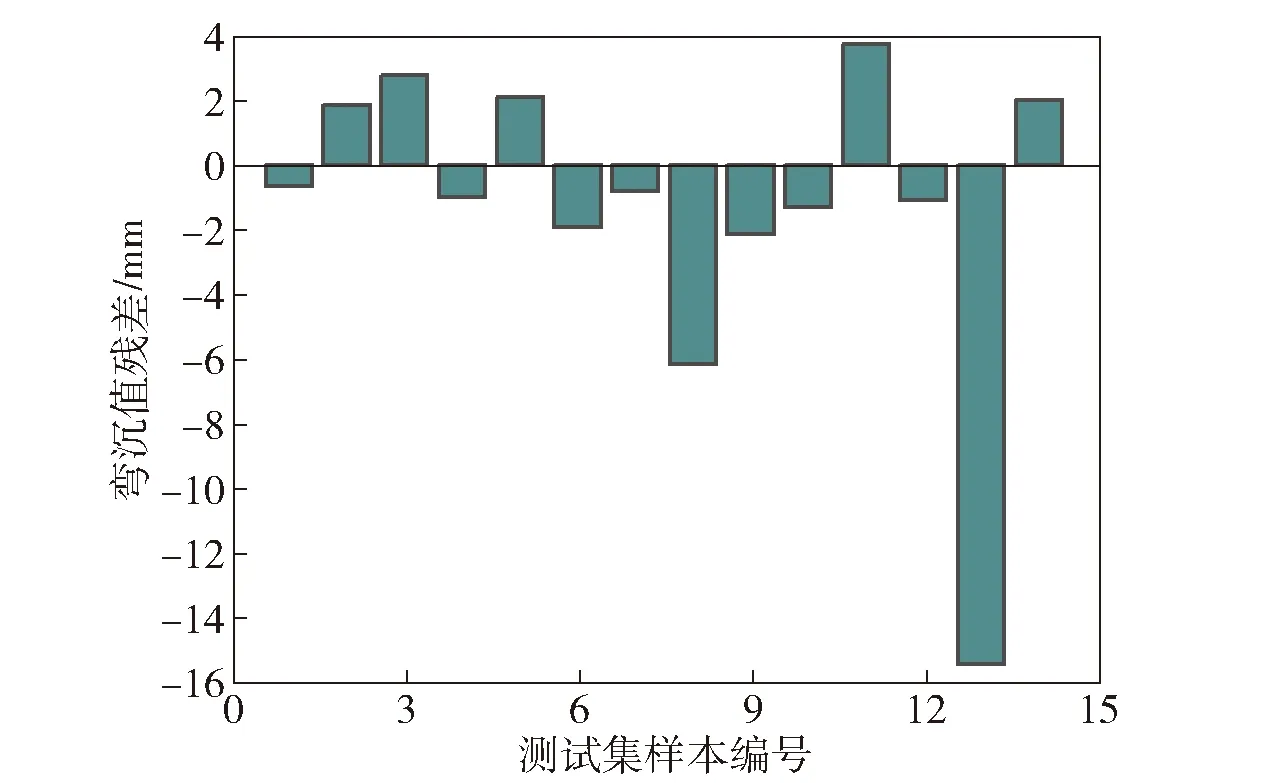
圖20 BP神經網絡模型殘差分析Fig.20 Residual analysis of BP neural networks model

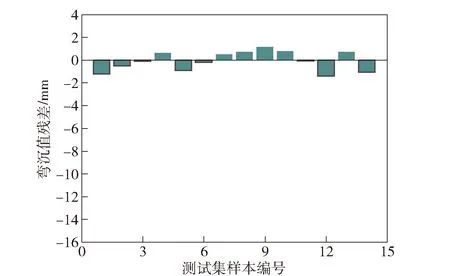
圖21 RBF神經網絡模型殘差分析Fig.21 Residual analysis of RBF neural networks model

在發射載荷下，3種預測模型的單個工況平均計算時間分別為2.8 s、2.1 s和39.8 s，單次有限元仿真所需時間為3.5 h。由此可見，預測模型計算時長遠小于有限元方法，RBF神經網絡算法預測模型既能滿足實時性要求，又滿足精確度要求。

綜合上述分析，在發射載荷下，RBF神經網絡算法模型對場坪可能的彎沉值同樣具有最優的預測能力。基于RBF神經網絡算法建立的近似模型可靠性強、可信度好，且可實現載荷已知情況下的實時預測，能夠極大地減少發射前選擇合適場坪的準備時間，具有重要的實用價值。

2.3 含未知結構參數的場坪承載能力預測算法

在對發射場坪進行選擇時，面層厚度、彈性模量和泊松比相對可控，通過查閱施工資料可以確定取值范圍。然而，對場坪承載能力影響較大的土基彈性模量受含水量等因素影響，變化幅度較大，難以測量。因此，基于本文前述計算結果，考慮圖22所示的層級網絡結構，以土基彈性模量未知、其他參數已知的發射場坪為研究對象，通過該場坪在起豎載荷下的動力學響應，反算該處場坪的土基彈性模量，并將計算結果與其他已知結構參數構成該處場坪的特征參數空間，從而對其在發射載荷下的可能彎沉值進行預測。

圖22 未知場坪承載能力快速預測的層級網絡結構Fig.22 Hierarchical network structure for rapid evaluation of bearing capacity of unknown launching site

對計算結果進行誤差分析，預測結果與仿真結果的平均誤差為10.46%。圖23為某未知發射場坪彎沉的預測值與有限元仿真值結果對比，結合圖24的殘差分析發現，對于土基彈性模量未知的發射場坪，此預測算法在一定誤差范圍內是有效的：對于承載強度較小的場坪，預測能力較弱，但預測值普遍大于有限元仿真值，仍具有一定的參考意義；對于承載能力較強的發射場坪，預測值與仿真值的殘差在±2 mm以內，預測能力表現較好，準確度較高。應用上述算法預測模型，能夠充分發揮發射快速性和隨機性的優勢，具有實際參考價值。

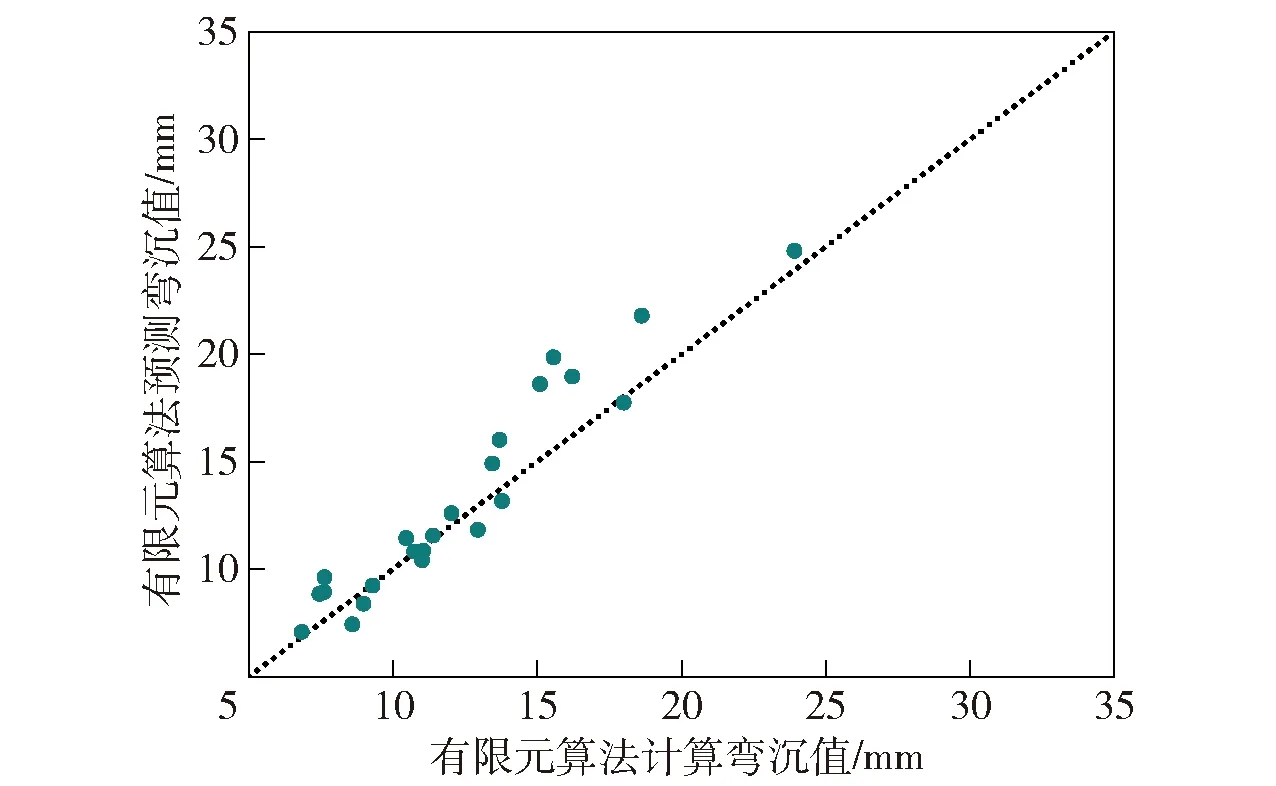
圖23 未知場坪承載能力預測算法方差分析Fig.23 Variance analysis of bearing capacity of unknown launching site by evaluation algorithm

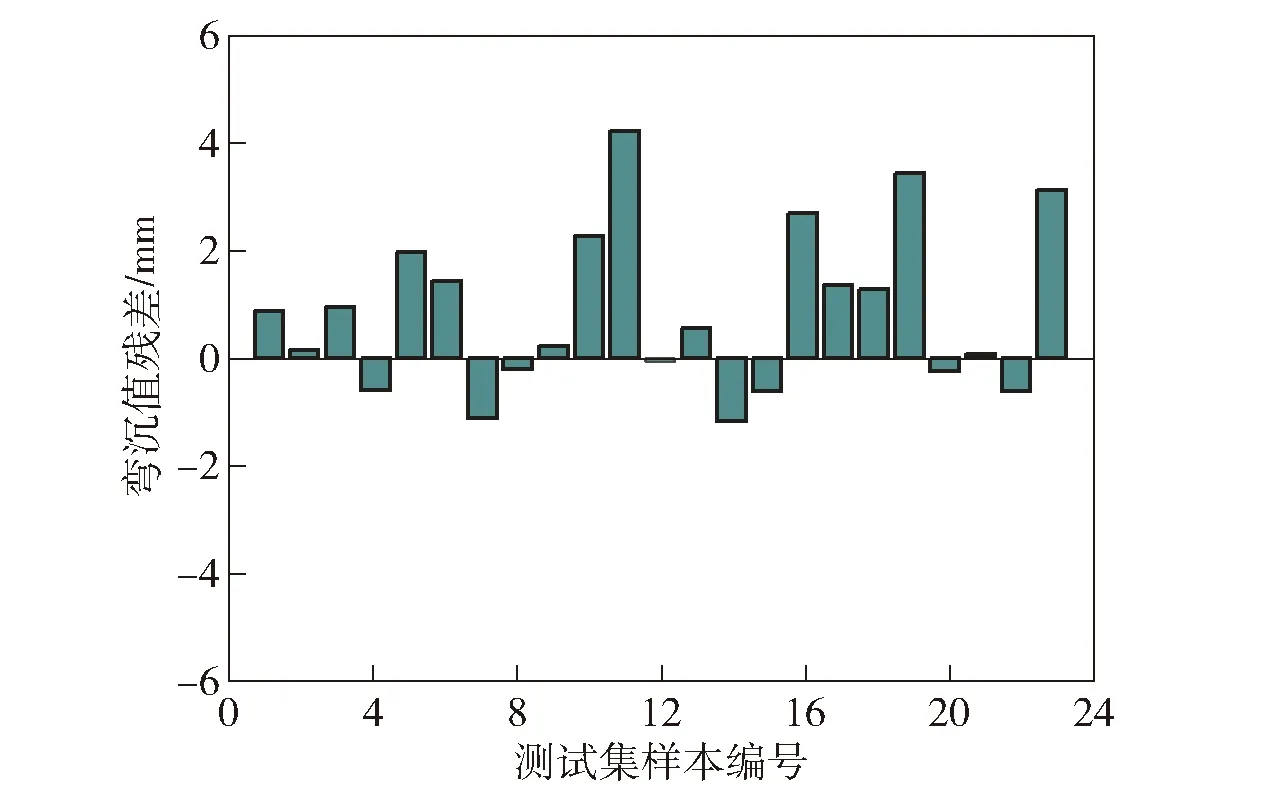
圖24 未知場坪承載能力預測算法殘差分析Fig.24 Residual analysis of bearing capacity of unknown launching site by evaluation algorithm

3 結論

針對無依托發射場坪承載能力的快速預測問題，本文基于線性多元回歸算法、BP神經網絡算法和RBF神經網絡算法建立了不同的近似模型。通過選取土基彈性模量和面層厚度兩個參數進行可視化校驗，證明優化拉丁超立方采樣方法是可行并有效的。通過對比分析研究，完成了對發射載荷下未知場坪承載能力的預測。得到以下主要結論：

1)在起豎載荷下，線性多元回歸模型和BP神經網絡模型預測結果的方差較大，尤其對于支撐強度較大的場坪樣本預測能力差距更為明顯。而基于RBF神經網絡建立的近似模型具有最優性能，平均誤差在10%以內，最大殘差0.059 9 mm，值為0.941，擬合度較高。

2)在發射載荷下，線性多元回歸模型、BP神經網絡模型和RBF神經網絡模型的殘差范圍分別在±4 mm、±4 mm和±1.5 mm。前二者在承載能力較強的場坪樣本中預測性能較好，但對承載能力較弱的場坪幾乎不可用。RBF神經網絡模型在全樣本集中表現優異，值為0.983，可以替代有限元仿真方法進行實戰化部署應用。

3)在實際發射過程中，無依托發射場坪的土基彈性模量受環境因素影響較難測得。本文創新點在于采用預測性能最優的RBF神經網絡算法，通過場坪在發射裝置起豎過程中的動力學響應，預測該場坪在發射載荷下的可能彎沉值。結果表明，該方法對承載力較強的場坪在發射載荷下彎沉值的預測結果殘差在±2 mm以內，具備充分的可信度，能夠用于導彈發射過程中場坪的快速選定決策。