基于激光自混合干涉調頻信號的位移測量實驗

韓玉祥,叢至誠,高丙坤,崔翔宇

(1.東北石油大學計算機與信息技術學院,黑龍江 大慶 163318；2.東北石油大學電氣信息工程學院,黑龍江 大慶 163318)

1 引 言

激光自混合干涉系統結構簡單、裝置緊湊、魯棒性好,能夠實現物體位移、距離、振動、速度、表面輪廓、透明物體厚度等高精度測量[1-12]。在干擾較小的環境中,大都采用激光器發射的調幅(AM)信號對目標進行測量,在滿足高精度測量要求的同時,結構更加輕量化,產品也更加實用化。但在大噪聲環境中,待測物體反射到激光自混合干涉系統中產生的相干調幅信號難以檢測,為此通過調頻(FM)信號測量目標物體狀態的方法陸續提出[13-16]。微位移測量已大量應用于大型土木結構、航空航天、健康監測等,故本文在激光自混合干涉平臺上,采用馬赫-曾德爾干涉儀,進行了調幅/調頻信號轉換與檢測；針對大噪聲干擾環境下的調頻信號,通過多次希爾伯特變換進行相位解卷,重構了待測信號,實現了微位移的高精度測量。

2 激光自混合干涉調頻測量原理

激光自混合干涉調幅/調頻轉換原理如圖1所示。其中,DFB為激光器,PD為光電探測器,PZT為微納米運動平臺,馬赫-曾德爾干涉儀用于實現AM/FM信號轉換[16]。

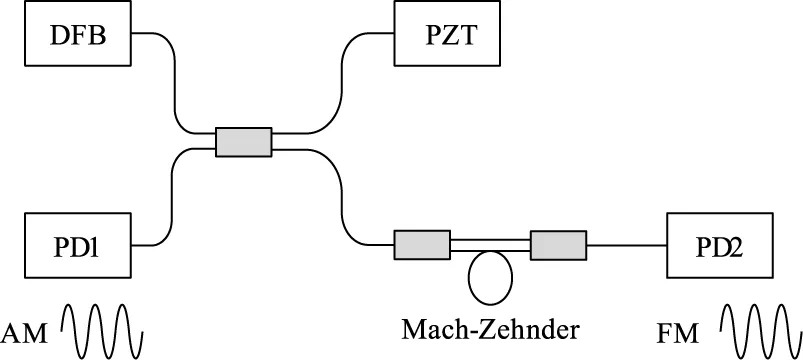
圖1 調頻信號產生原理圖Fig.1 Frequency modulation signal generation schematic diagram

激光自混合干涉系統調幅信號的功率方程為[10]:

P=P0[1+βcos(ωτ)]

(1)

式中,P是有光反饋時的光功率;P0是無光反饋時候的初始光功率;β表示激光自混合干涉中的條紋可見度;ω為角頻率;τ為光束在外腔往返一次所需要的時間。

自混合干涉系統的頻率方程為:

ωτ=ω0τ-Csin(ωτ+arctanα)

(2)

式中,ω0為無光反饋時候的初始角頻率；C為光反饋強度系數；α為線寬增強因子,系激光器的屬性參數。用光頻率表示的頻率方程為:

2π(f-f0)τ=-Csin(2πfτ+arctanα)

(3)

令Δf=f-f0,有:

(4)

當自混合干涉信號經過馬赫-曾德爾干涉儀后,通過線性擬合,干涉儀輸出功率PFM為:

PFM=P0SΔf=Asin(2πfτ+arctanα)

(5)

式中,A為光束電矢量的振幅；S為干涉儀的強度傳輸系數T對光頻率f的導數,即:

(6)

式中,n為光纖纖芯的折射率；c為光在真空中的速度；ΔL為振動位移。

由式(6)可知,調節馬赫-曾德爾干涉儀的S可對光束濾波,其強度傳輸系數T與光頻率f的對應變化曲線如圖2所示。

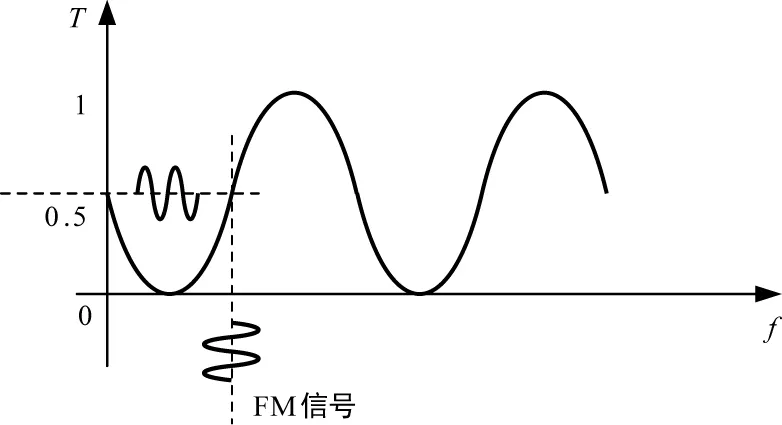
圖2 濾波器強度傳輸系數與光頻率的對應變化曲線以及FM信號轉換原理圖Fig.2 The corresponding change curve of filter intensity transmission coefficient and light frequency and the schematic diagram of FM signal conversion

由圖2可知,當T=0.5時,S取得最大值,即:

(7)

可見馬赫-曾德爾干涉儀濾波后得到的調頻信號為正弦信號,因為相位信息難以解調,故通過多重希爾伯特變換[17],得到與原信號PFM正交的信號PN:

PN=Acos(2πvτ+arctanα)

(8)

綜合式(5)和(8),可計算出在進行位移重構時所需要的相位:

(9)

根據自混合干涉調幅信號與經過干涉儀濾波后的調頻信號之間對應的相位關系,結合式(1)和(5),兩信號之間的相位關系可以表示為:

(10)

分別對調幅和調頻信號進行探測,然后對其進行相位提取,即可對線寬增強因子進行求解。

激光自混合干涉相干項的相位與外腔長度變化的關系為:

(11)

式(11)反映了相位與外腔長度變化的對應關系,實現了相位解卷。結合上面有關相位公式,即可進行位移重構,恢復出待測物體微位移軌跡。

3 微位移測量數值模擬

基于上述原理,首先通過數值模擬驗證方法的有效性,分析微位移測量精度。選擇外部物體運動頻率為100 Hz,振幅為3.1 μm,初始相位為0的簡諧運動。激光器模擬波長為1550 nm,線寬增強因子α為4.6,光反饋因子C取為0.1,采樣點數取為4000,可得到無噪聲時調頻信號仿真結果如圖3所示。圖3(a)中,“a”線為調頻信號,“b”線調頻信號經過希爾伯特變換后的信號。在圖3(b)中,“a”線為模擬外部物體的簡諧運動,“b”線為重構曲線,二者幾乎重疊。圖3(c)給出了重構位移與模擬位移的誤差,可見該方法能夠實現微位移的高精度測量。

圖3 無噪聲下調頻信號仿真Fig.3 Simulation of frequency modulation signal without noise

對前述系統加入10 dB的高斯白噪聲,數值仿真結果如圖4所示。圖4(a)中,“a”線為加噪調頻信號,“b”線為希爾伯特變換后的信號。在圖4(b)中,“a”線為模擬外部物體進行的簡諧運動,“b”線為去噪后位移重構曲線。圖4(c)給出了重構位移與模擬位移之間的誤差。可見,在大噪聲環境下,基于調頻信號的重構仍具有很高的精度。

圖4 加入10 dB噪聲的數值仿真Fig.4 Numerical simulation with 10 dB noise

4 微位移信號的測量與分析

數值模擬和分析證明了本文提出的高精度微位移測量方法的有效性,為此開展實驗測試,裝置如圖5所示。為模擬大噪聲干擾環境,該實驗選用的光源為無光隔離器無溫控的光纖耦合的DFB激光器(THORLABS,S1FC1550PM),波長為1550 nm,使用的三個耦合器均為3 dB標準耦合度(分光比為50∶50),耦合器的四個傳感臂的插入損耗分別為3.32 dB、3.37 dB、3.46 dB、3.60 dB。第一個耦合器一條輸出臂連接準直鏡頭(THORLABS、F220FC-1550)照射在振動物體表面,振動物體選用鏡面,放置在PZT(P753.1CD,PI)上,反射光再通過耦合器反射回激光腔形成自混合干涉現象,通過PD1(THORLABS,PDA20CS2)進行探測。耦合器另一條輸出臂連接馬赫-曾德爾干涉儀,干涉儀由兩個3 dB耦合器和一段1 m的光纖(THORLABS,P1-1550A-FC-1)組成,再連接到PD2(THORLABS,PDA20CS2)進行調頻信號的探測。PD1和PD2都通過數據采集模塊(USB-4431,NI)獲取電壓信號,并在PC機上進行處理。在本次實驗中,所有實驗器材均放置在光學隔振平臺(T1225QK,THORLABS)上,以避免外界振動的干擾。

圖5 振動物體調幅/調頻信號檢測實驗裝置圖Fig.5 An experimental device for detecting AM/FM signals of vibrating objects

設置目標物體振動頻率為5 Hz,振動峰峰值為3.1 μm,采樣頻率設為50 kHz,兩個光電探測器同一時刻探測到的調幅和調頻信號如圖6所示。可以看出,調頻信號的振幅遠大于調幅信號且比較光滑,有利于相位解卷。

圖6 同時采集的調幅和調頻信號Fig.6 Amplitude and frequency modulation signals are collected simultaneously

根據前述激光自混合干涉調頻測量原理,基于采集到的調頻信號進行微位移重構,結果如圖7所示。圖7(a)中,“a”線為采集到的調頻信號,“b”線為調頻信號經過希爾伯特變換后的信號。在圖7(b)中,“a”線為外部物體振動曲線,“b”線為重構曲線。圖7(c)給出了調頻重構信號與原信號之間的誤差,可見,基于調頻信號可直接實現位移重構,誤差在100 nm以內。

圖7 基于調頻信號的微位移測量實驗結果Fig.7 Experimental results of micro displacement measurement based on frequency modulation signal

因為使用調幅信號難以直接進行位移重構,故首先對調幅信號做低通濾波,再進行位移重構,結果如圖8所示。圖8(a)中,“a”線為濾波后的調幅信號,“b”線為希爾伯特變換變換后的信號。在圖8(b)中,“a”線為外部物體振動曲線,“b”線為重構曲線。圖8(c)給出了調幅重構信號與原信號之間的誤差,可見,濾波后的調幅信號進行位移重構的誤差達到了520 nm。

圖8 基于調幅信號的微位移測量實驗結果Fig.8 Experimental results of micro-displacement measurement based on amplitude modulated signal

調整物體的位移,同時獲取兩調頻和調幅信號,按照前述方法分析其信噪比,得到三組數據示于表1。可見,調頻信號的信噪比遠高于調幅信號的信噪比。

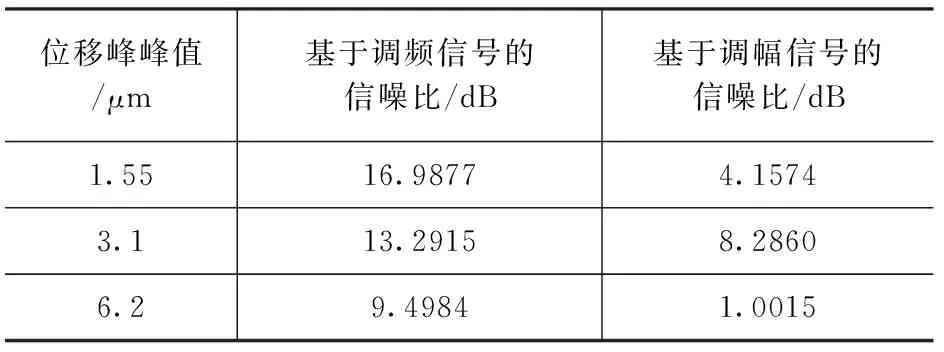
表1 調頻和調幅信號的信噪比Tab.1 The signal-to-noise ratio of FM and AM signals

5 結 論

(1)基于激光自混合干涉系統,利用調頻信號進行微位移測量,誤差在100 nm以內,明顯低于利用調幅信號測量的誤差,適用于超精密測量。

(2)基于激光自混合干涉系統測量微位移,調頻信號的信噪比遠高于調幅信號的信噪比,適用于大噪聲環境下高精度測量。