面向GPU計算平臺的神經網絡卷積性能優化

李茂文 曲國遠 魏大洲 賈海鵬

1(中國科學院計算技術研究所 北京 100190) 2(中國航空無線電電子研究所 上海 200241)

近年來，隨著卷積神經網絡技術的發展，越來越多的算法應用于機器視覺的各種任務中，如目標分割、檢測、跟蹤、識別等[1].基于深度學習的目標檢測算法相比于傳統方法通常能實現更高的精確度，因此在各種硬件平臺上都得到了廣泛的應用，但是卷積神經網絡通常伴隨著較高的計算復雜度，制約著算法在各個平臺上的使用，如何提升和最大化硬件的使用效率來進一步優化卷積神經網絡的性能就顯得至關重要.另一方面，運行卷積神經網絡的這些硬件平臺存在一定差異，一種通用、跨平臺的工作非常有意義.英偉達公司提供的統一計算設備架構(compute unified device architecture, CUDA)軟件支持只適用于英偉達GPU硬件平臺，對于其他GPU平臺如ARM GPU，AMD GPU等硬件平臺來說，開放運算語言(open computing language, OpenCL)[2]是第1個面向異構系統通用目的并行編程的開放式免費標準，也是一個統一的編程環境，便于軟件開發人員為高性能計算服務器、桌面計算系統、手持設備編寫高效輕便的代碼，而且廣泛適用于多核心處理器(CPU)、圖形處理器(GPU)以及數字信號處理器(DSP)等其他并行處理器.

卷積運算在整個神經網絡中占比時間經常在80%以上，在部分主要以卷積進行構建的網絡中占比時間能達到95%甚至更高.而卷積操作在訪存量和計算量都很大，并且相關工作的算子相對獨立難以合并，在深度學習的卷積規模上的優化加速效果有限.針對這些問題，本文實現了一種面向卷積神經網絡的卷積優化方法：通過配置相關參數生成各種不同訪存、計算規模的通用矩陣乘(general matrix multiplication, GEMM)或Winograd算子，以及算子合并方法對卷積進行優化；結合自調優選擇出不同算子中性能最優的算子實現方法，應用到卷積神經網絡中，并通過AMD V1605B平臺上的實驗證明了本文工作的效率.

本文的主要貢獻有3個方面：

1) 卷積優化的新方法.針對現有GEMM算法的不足以及深度學習網絡規模特點，提出了GEMM優化方法.

2) 在GEMM工作基礎上提出Winograd優化方法，并結合算子合并來對卷積進一步優化.

3) 通過自調優的辦法，尋找到卷積的最優實現.

1 相關工作和原理

1.1 相關工作

已經有很多文獻在軟硬件方面提出了針對不同硬件平臺、框架實現了對卷積神經網絡優化方法[3-4].其中大部分算法是針對卷積神經網絡中的卷積層進行優化，卷積有多種實現方式：直接實現、轉換成GEMM進行實現，或者通過變換轉換成傅里葉變換算法再進行實現.而越來越多的其他平臺，比如硬件加速器[5]從硬件角度上解決問題.

憑借著優秀的性能，通過將卷積轉換成矩陣乘法GEMM算法來加速卷積，并在此基礎上優化GEMM來實現進一步加速成為一種重要的方法.主要的GEMM算法實現有MIOpenGEMM[6]，CLBlas[7]，CLBlast[8]，cuDNN[9]，cuBLAS[10]，OpenBLAS[11]等.英偉達公司的cuDNN軟件庫與cuBLAS，使用CUDA軟件架構，專門應用于英偉達平臺的GPU設備，OpenBLAS主要圍繞CPU進行優化，兩者都不是圍繞著OpenCL開展的.基于OpenCL的GEMM優化工作中，深度學習卷積通過GEMM算法提升性能，并結合形如clCaffe[12]等框架執行.AMD公司開發了ROCm平臺[13]，其中的MIOpen深度學習軟件加速庫依靠MIOpenGEMM實現；CLBlas，CLBlast兩者針對科學計算應用有著較好的加速，并通過Caffe-OpenCL加速庫實現對深度學習的加速.

大部分使用GEMM算法針對神經網絡進行加速的性能優化中，都是將GEMM算法作為獨立的算子.這些將GEMM算子獨立使用的算法庫，將GEMM算子獨立于整個應用之外，沒辦法跟深度學習應用進行進一步算子融合，往往限制了整個深度學習應用的性能.

1.2 神經網絡與卷積變換原理

常見的基于深度學習的目標檢測算法主要分為2類:基于候選區域和基于回歸.基于候選區域的深度學習目標檢測方法以候選區域為前提，首先在圖像中搜索候選區域，再針對產生的大量候選區域進行分類.代表典型方法有R-CNN，Fast R-CNN，Faster R-CNN等算法[14].基于回歸的深度學習目標檢測方法主要采用回歸的方法，將整個目標檢測過程視為一個回歸問題，不需要花費時間提取多余的候選區域，屬于一種端到端的方法.典型代表有YOLO[15]，SSD等方法.

卷積神經網絡使用的卷積包含多種參數，使得卷積存在多種類型.對于YOLO網絡來說，最常見的是沒有特殊參數的普通卷積，計算過程如圖1所示.對于不同步長(stride)以及輸入的寬度W1和高度H1來說，會有不同的輸出W2和H2.

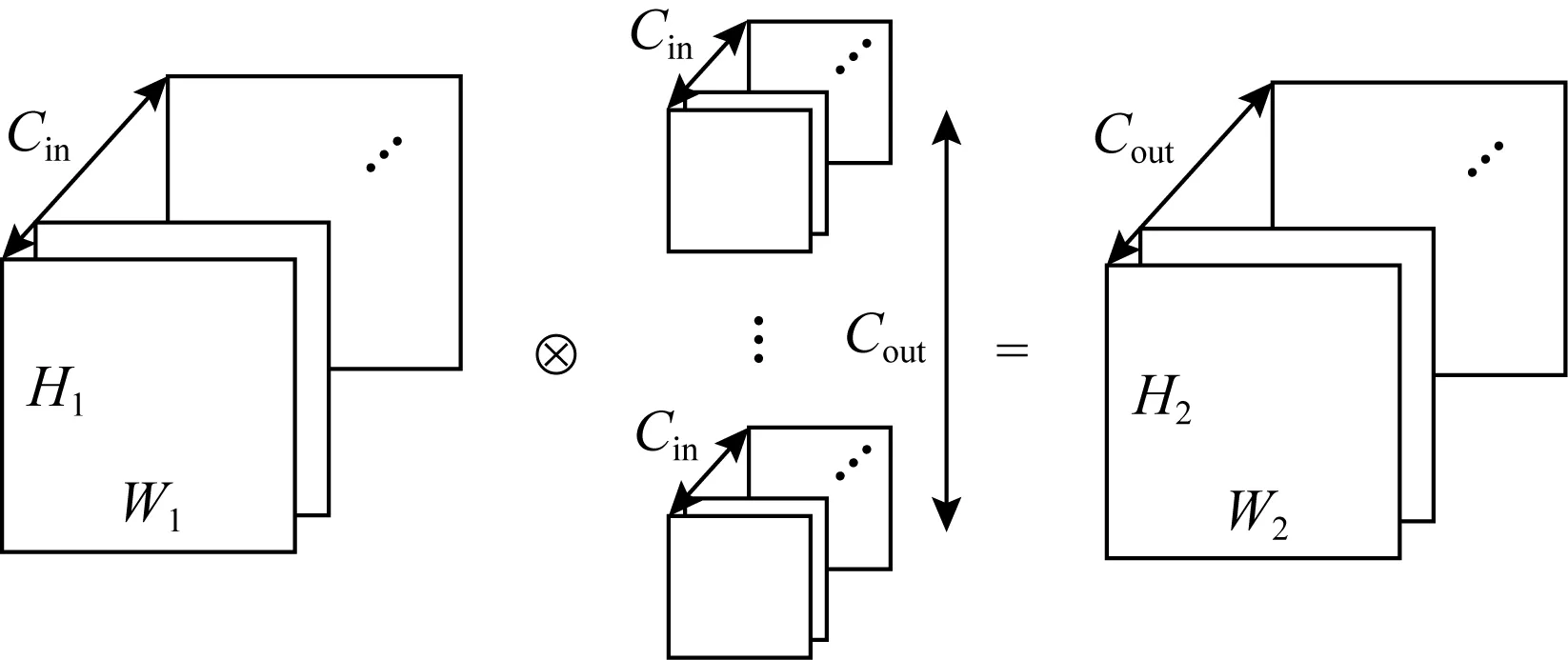
Fig. 1 General convolution圖1 普通卷積

普通卷積可以通過圖像變換矩陣方法Im2col，將卷積轉換成矩陣乘法[16].因為卷積的權重數據是連續存儲的，可以直接用于矩陣乘法，所以只需要將輸入數據進行變換，將輸入的多維數據轉換成2維矩陣，即可與權重參數矩陣做GEMM矩陣乘法來實現卷積.從實踐來看，GEMM算法可以有效提升方寸的效率和卷積的性能，優化卷積性能的問題也轉化成了GEMM算法優化的問題.Im2col中輸入數據的具體轉換方法如圖2所示.

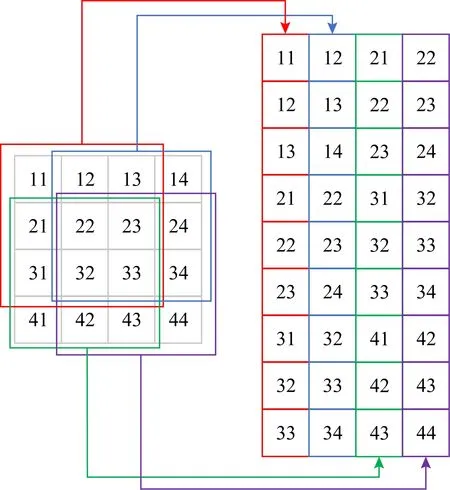
Fig. 2 Im2col transformation圖2 Im2col變換

GEMM的一般形式是C=α×A×B+β×C，其中矩陣A和B包含輸入數據轉換之后的情形.常見的情況是α=β=1，對于GEMM規模為M×N×K來說，矩陣A，B，C是輸入，矩陣A的規模為M×K，矩陣B的規模為K×N，矩陣C的規模為M×N.計算過程如圖3所示:

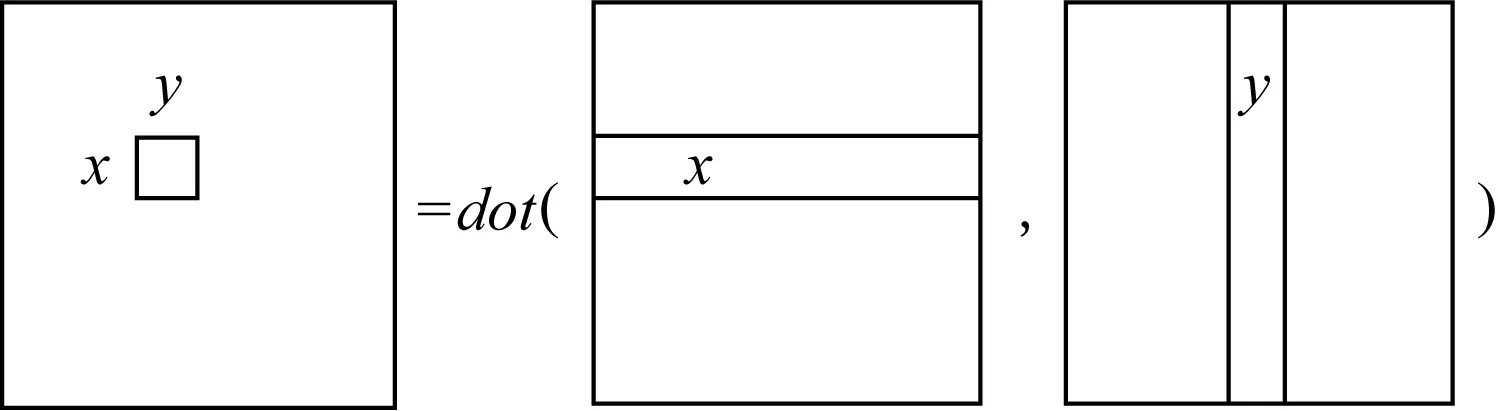
Fig. 3 Cx,y process圖3 Cx,y計算過程

當矩陣A,B比較小時，根據計算機體系結構可知，當從RAM中讀取矩陣A,B的內存，根據局部性原理可以將矩陣A,B放到緩存(cache)中，因為CPU訪問cache比訪問主存快.但卷積神經網絡中的卷積大部分規模比較大，通常大小會超過cache.當矩陣A,B較大時，即超過cache大小，根據矩陣乘的普通方法，由于訪問“行優先存儲的矩陣B”的內存不連續(讀取矩陣B的1列)，造成緩存cache頻繁地換入換出.

普通卷積的偽代碼如算法1所示.

算法1.普通GEMM算法.

① forxin [1,2,…,M]

② foryin [1,2,…,N]

③ forzin [1,2,…,K]

④Cx,y+=Ax,z×Bz,y;

⑤ end for

⑥ end for

⑦ end for

因此采用分塊的方法來對GEMM進行加速，可以有效地提升cache命中率、增加內存復用，從而提升效率.除了算法1中提到的部分，還需要額外增加分塊方法的大小，如圖4所示:

Fig. 4 Block computing method圖4 分塊計算方法

采用m,n,k這3個參數來指定分塊,分塊將原來的訪存空間分成若干個m×n×k的小塊，需要執行m0次的按塊索引和n0次的循環，在m×n×k的小塊內進行GEMM算法并將結果疊加k0次.最終將結果輸出到矩陣C.對于通常的卷積來說，M，N，K都是2的冪次，因此m,n,k都可以取8，16等值.具體算法如算法2所示:

算法2.分塊GEMM算法.

/*算法中的gemm表示普通GEMM算法*/

①m0=M/m;

②n0=N/n;

③k0=K/k;

④ forxin [1,2,…,m0]

⑤ foryin [1,2,…,n0]

⑥x0=x×m,y0=y×n;

⑦C[x][y]=0;

⑧ forzin [1,2,…,k0]

⑨z0=z×k;

⑩A[x][z]←A[x0,x0+1,…,x0+

m][z0,z0+1,…,z0+k];

k][y0,y0+1,…,y0+n];

B[z][y]);

y0+1,…,y0+n]←C;

最常見的是以景起句。如辛棄疾《卜算子·荷花》的起句，簡單的十個字便描摹出了荷花的形態，并運用“紅”“翠”兩個色彩詞，視覺效果即刻突出。再如李處全《卜算子·即席奉女兄壽》，起句中“斗”字的運用讓芍藥有了擬人化的動態效果，正似“對鏡貼花黃”的嬌娘子；而“飛”字又巧妙地借“飛雪”之輕盈飄渺的姿態給人以想象空間，頓感三月楊柳飄絮正如寒冬之雪花。再如范成大《卜算子·云壓小橋深》，開篇“云壓”二字就為全詩奠定感情基調，為下文梅花被雪壓不已，又再次布滿橫窗影的遭際張本，即被雪壓不已，又再次布滿橫窗影。

YOLO目標檢測方法中，使用的主要是普通卷積，因此將其轉變換成GEMM是一種主要的優化方法，但存在一些問題，以YOLOv2的網絡模型為例來說明.表1所示的是共30個網絡層的YOLOv2網絡模型中的卷積層及其變換成GEMM以后的參數，其中進行計算的矩陣A的規模為M×K，矩陣B的規模為K×N.

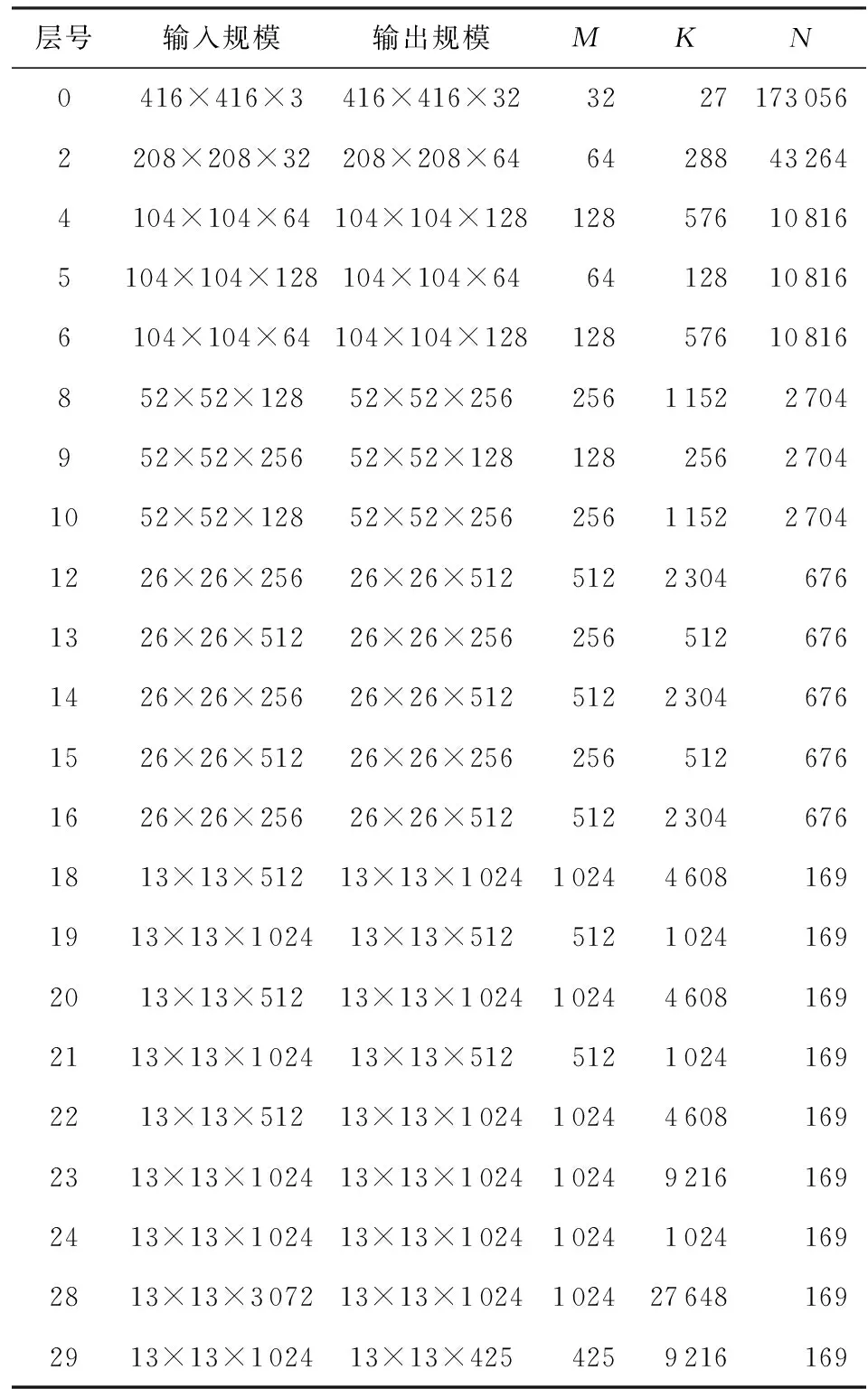
Table 1 Calculation Parameters After ConvolutionConversion GEMM Algorithm表1 卷積轉換GEMM算法后的計算參數

表1的數據能夠明顯看出4種情況：

1) 計算參數變化大，存在極小值、較小值情況.M,N存在較小值的情況，比如N=169和M=32.而現有的GEMM算法加速庫的訪存分塊規模更多考慮大規模矩陣計算，這使得對于M，N，K只有部分較小時，針對大規模矩陣乘法的分塊、訪存、計算的方法，會存在計算、訪存資源不能夠充分利用的問題.

2) 分塊參數不能被整除，存在計算分支.進行GEMM運算，在M,K,N不能被整除時，并行計算存在余數分支的問題.常用的GEMM算法加速庫生成算子時只生成M,K,N都存在余數分支或者都不存在余數分支這2種情況，不討論M,K,N其中僅有部分參數存在余數分支的問題.而深度學習卷積中，通常僅有N參數有較常見的分支，對所有參數都進行分支判斷會造成計算資源的浪費，影響并行效率.

3) 計算參數比例變化大.進行GEMM運算的2個矩陣的形狀和參數比例是不斷變化的，比如第0層網絡層的矩陣A的M,K很小，均不高于32，但N非常大；第28層網絡層中，M,K非常大，而N非常小.現有的GEMM算法加速庫的訪存分塊大小又通常為1∶1的正方形，如32×32,64×64等，這使得訪存計算低效.

4) 只優化卷積，無法進行多算子合并.常用的GEMM算法加速庫生成的時候只能使用卷積算子，無法進行多算子合并，影響網絡效率.

2 卷積優化加速方法

2.1 GEMM優化原理

算法3.本文面向GPU的GEMM算法.

/*算法中lut表示讀取配置信息，Synchronize(thread)表示對GPU線程進行同步*/

①m,n,k,gtx,gty←lut(M,N,K);

②m0=M/m,n0=N/n,k0=K/k;

③mthr=m/gtx,nthr=n/gty;

/*設置工作組(thread_group)規模為(m0,n0),每個工作組id為(gx，gy),在每個工作組內設置共享內存AS[m][k],BS[k][n]*/

④ forthread_group(gx，gy) inrange(m0,n0)

⑤ 共享內存AS[m][k],BS[k][n];

/*每個工作組內工作項(thread_item)規模為(gtx，gty)，每個工作項id為(tx，ty),每個工作項設置本地數組

CL[mthr][nthr]*/

⑥ forthread_item(tx，ty) inrange(gtx，gty)

⑦ localCL[mthr][nthr];

⑧x0=gx×m,y0=gy×n,CL[1,2,…,mthr][1,2,…,nthr]=0;

⑨ forzin [1,2,…,k0]

⑩z0=z×k;/*將數據塊從CPU傳

到GPU共享內存*/

xi×gtx][z0+zi]×

BS[z0+zi][ty+yi×gty];

其中thread_group表示在OpenCL實現中工作組的分組，thread_item表示每個工作組中的工作項，memory_barrier_among_thread()同步不同線程之間的操作.但是如表1所示，存在著較多的N不為16倍數的情況，因此對于GEMM算法來說就產生了很多的分支和判斷，降低了算法的并行度和效率.同時硬件的訪存效率對GEMM算法的影響也至關重要，對于M,N較小的情況來說，采用固定大小進行分塊來實現對不同尺度的、規模的矩陣進行支持，也顯得不夠.

為了解決表1中存在的問題，并進一步提升并行算法效率，我們在工作中采用代碼生成的策略.即增加對各種不同類型的算法參數進行配置，通過特異性的算法參數來解決不同規模下的GEMM算法性能問題，主要包括3種配置方式：

1)m，n，k分塊參數可變、可配置

對于算法2中進行分塊的參數m，n，k，不再采用固定值進行配置和計算，而是可變參數，使得分塊大小能夠提高訪存效率.

m，n，k參數跟gtx,gty有關，同時要考慮執行算法硬件的硬件參數.針對常用的GPU架構，m，n，k取值范圍通常為16的整數倍.而k的取值對分塊的影響有限，主要是對循環的影響較大，因此需要配置較多參數的主要是m，n，而且需要配置足夠多的m，n.

2)M,N,K余數計算分支可變、可配置

規模不為整數倍會導致存在分支，但卷積神經網絡的參數并不是M,N,K都會導致分支存在，因此根據參數情況去配置算法執行分支的部分變得尤為重要.

m，n，k取值為16的整數倍，當不為16的整數倍時，往往M,N,K存在著余數，因此需要執行分支語句來完成對邊界的正確運算以保證正確性.分支對于并行異構設備往往造成了運算資源的浪費，因此需要盡可能減少分支存在的情況，生成存在盡量少的分支代碼.

3)gtx,gty訪存計算比例

常用的訪存、計算比例通常為1∶1，即緩存AS,BS這2個矩陣的數據每次采用8×8，16×16，32×32，64×64這樣的分塊訪存、緩存、計算的規模，但對于可變參數來說，可能遇到比例不一致的情況，如分塊、計算的規模為32×64等，也產生了相應的分支和算法配置.

由于各種參數對代碼的影響因素較多，因此對于不同的M，N，K，正確選擇GEMM算法配置的參數，能夠使得GEMM運算效率最大化至關重要.

根據算法需要執行的數據規模，即M,N,K大小，生成所有可用的GEMM算法代碼以后，遍歷所有的GEMM算法代碼，尋找到最優性能的配置保存下來.在卷積神經網絡執行推理時，通過LUT函數讀取配置.

2.2 Winograd優化原理

基于2.1節中的GEMM優化原理，本文提出了通過一系列變換以及GEMM算子來實現Winograd算法并實現卷積優化加速的方法.

Winograd算法越來越多地被應用在了卷積加速上[17].Winograd算法在計算設備上進行加速的主要原理是使用了更多的加法來代替GEMM算法的乘法，從而提高在計算機設備上的性能.Winograd算法的原理與證明過程在此不再贅述，主要介紹適用于卷積的Winograd，以輸入數據d為4×4、卷積核心g為3×3的卷積為例，輸入d,g，輸出Y為

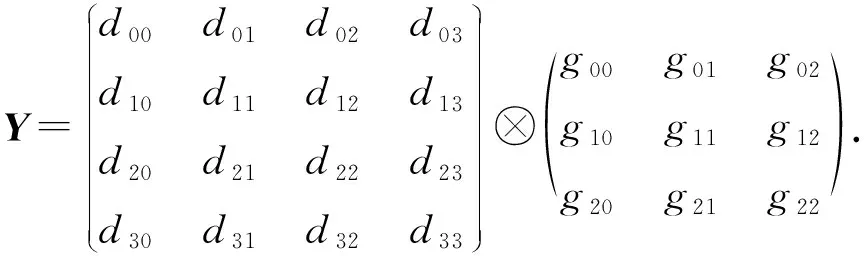
(1)

卷積的實際計算中，把卷積數據分為4×4的數據塊，針對每個塊應用F(2×2,3×3)的計算公式，從而可以降低運算強度，提高性能.其中，參數2×2意味著從輸入數據矩陣上面滑窗的步長為2×2，參數3×3意味著卷積核心為3×3的規模.使用Winograd的F(2×2,3×3)計算為

Y=AT((GgGT)⊙(BTdB))A.

(2)

其中，中間變量G，BT，AT分別為

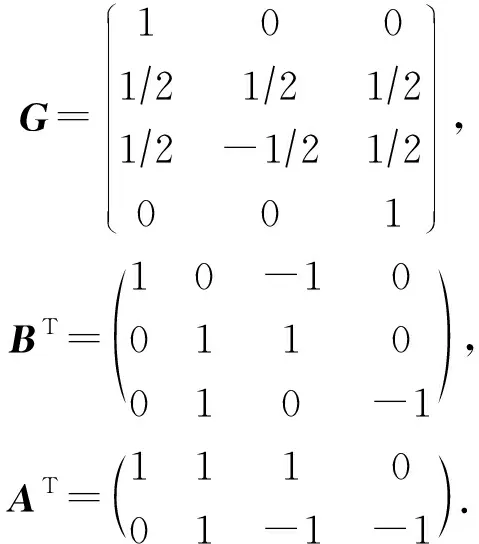
(3)

該算法進一步拆分成4個步驟：

1) 卷積核心GgGT變換

對卷積核心(kernel)g進行變換:

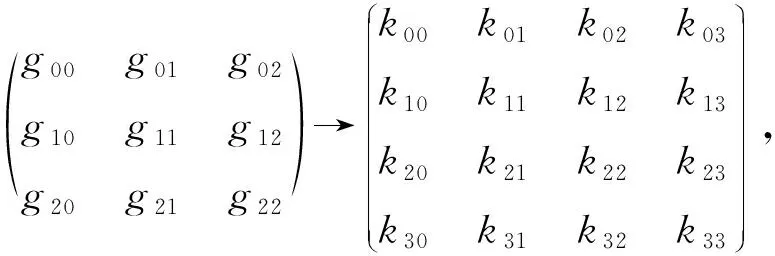
(4)

其中，列對應于輸入通道，行對應于輸出通道.表格中的每個元素包含了16個數值4×4,也就是按照公式GgGT從一個3×3的核心中計算出來的值.對于進行多次處理、視頻處理等情況，卷積核心變換后的數據可以復用，以提升速度.變換后的結果為

1 2 …cin

2) 輸入數據BTdB變換

對輸入數據進行變換時，先將輸入數據重組視為1個矩陣數組，行數為cin，將每一行連續拼接，共有len1列，其數據存儲為

1 2 …len1

對于第1行第1列的矩陣d進行變換后BTdB的輸出為

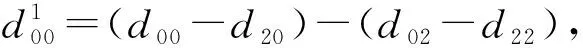
1 2 … (w2+1)(h2+1)/2

3) 4×4規模點積

無論是卷積核心還是輸入數據，變換后的結果都是4×4規模的數據.卷積的執行過程中，輸入數據為w1×h1×cin規模，輸出數據為w2×h2×cout，會產生cout×cin組4×4規模的卷積核心變換，以及cin×floor((w2+1)/2)×floor((h2+1)/2)組4×4規模的卷積輸入數據變換.因此產生cout×cin×floor((w2+1)/2)×floor((h2+1)/2)次4×4規模的點積，可以轉換成4×4次即16次的矩陣乘法，直接調用算法1.

4) 計算結果ATCA變換

通過對4×4規模點積的計算結果C進行ATCA變換，獲取最終的輸出Y.

2.3 算子合并

卷積在進行運算時，通常跟后續的算子操作有一定的關聯，因此可以進行算子合并.通過將算子合并，在OpenCL軟件中有諸多好處：

1) 可以節省存儲中間結果的空間；

2) 減少對內存的讀寫；

3) 減少函數的調用與內核啟動(kernel launch)時間.

卷積的數學表達式是yconv=w?x+b，可以與卷積進行合并的算子主要有3種方式：

1) 與batchnorm進行合并

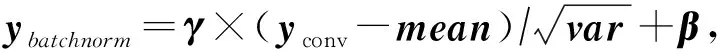
2) 與激活函數合并

激活函數activate是一類函數，常用的激活函數有sigmod，tanh，ReLU，LeakyReLU，ReLU6等.激活函數通常的算式是yactivate=activate(yconv)，融合以后新函數公式是yactivate=activate(w×x+b).

3) 與eltwise合并

eltwise算子的操作有3個：點乘(product)、相加(sum)、取最大值(max).由于卷積轉換成GEMM算法，GEMM計算的表達式為C=α×A×B+β×C，可以和eltwise算子進行合并，當進行eltwise算子的sum操作時，eltwise算子為yeltwise=yconv+x1，與GEMM公式合并以后的結果為C=A?B+C.

3 神經網絡與卷積自適應調優優化

第2節生成了各種規模的GEMM算子，還需要結合神經網絡參數進行自適應調優，選擇出性能最好的卷積算子，以便于完成卷積神經網絡的處理.

3.1 神經網絡配置

通過神經網絡的配置，獲取卷積與網絡的配置信息，分析、計算卷積對應的變換后的GEMM和Winograd參數信息，以及計算算子合并的信息.為后續算子合并、生成GEMM代碼提供足夠的配置信息和參數信息.整個網絡的處理流程如圖5所示：

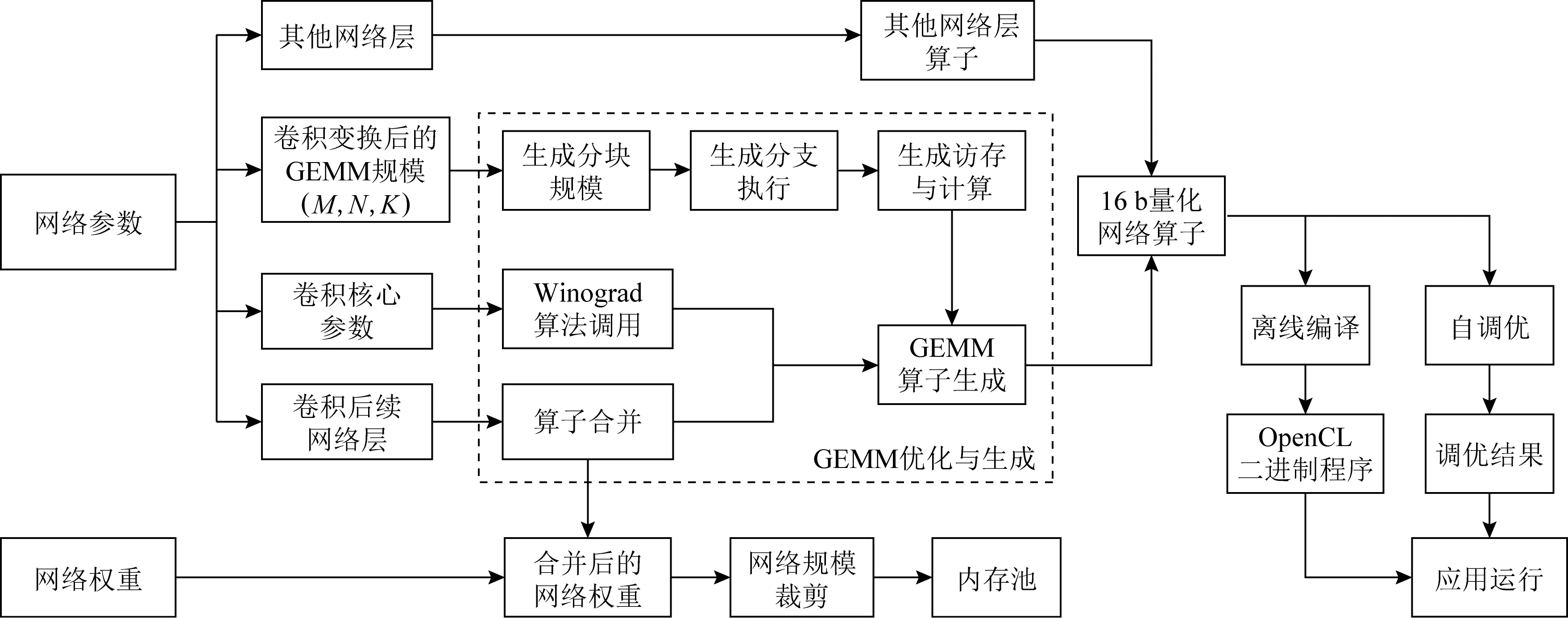
Fig. 5 Neural network convolution optimization process based on OpenCL圖5 基于OpenCL的神經網絡卷積調優過程

3.2 GEMM優化生成與卷積自調優

卷積神經網絡中的GEMM代碼配置因素較多，主要包括6個配置方面：

1)m,n,k分塊規模

根據GEMM規模(M,N,K)來進行配置.

2)M,N,K執行分支

根據GEMM規模(M,N,K)來進行配置.

3)gtx,gty訪存計算比例

根據GEMM規模(M,N,K)來進行配置.

4) 是否用于Winograd

根據卷積核心參數進行配置.

5) 算子合并

根據卷積后續網絡層情況進行配置.

6) 網絡16 b量化

根據需求是否適用16 b量化.

由于GEMM代碼配置因素多，因此生成的不同規模下、場景下的GEMM代碼非常多.為了實現GEMM算法的效率最大化，采用自調優的辦法.即在生成了網絡算子以后，還需要對網絡進行自調優，得到該網絡的GEMM效率最優的參數.網絡調優采用遍歷調優的方法，對所有可能的算子進行測試和運算，對于可能執行Winograd的卷積，將Winograd實現也一并進行對比，將對比得到的最優輸出結果的配置參數輸出為調優結果，便于運行時進行調用.

3.3 OpenCL離線編譯

在線編譯是指在宿主程序中引用內核的源代碼來構建OpenCL程序.進行在線編譯時，內核通過運行時環境中的OpenCL API庫編譯內核函數的源代碼.這種方法不適用于需要達到實時效果的嵌入式系統.同時，由于內核程序可以從主機程序中讀取，因此不適合商業應用.離線編譯是指OpenCL主機可以直接在目標設備上運行編譯好的二進制程序.離線編譯時，內核程序使用OpenCL編譯器預先編譯二進制文件，OpenCL API在宿主程序中調用編譯后的二進制文件.由于二進制執行文件是在主程序中直接調用的，所以從主程序啟動到內核運行之間的時間非常短,能夠有效提升框架的速度和性能.

3.4 內存池

在卷積神經網絡進行推理時，使用的數據量較大，占用較多的內存資源；同時對于臨時數據的變換也需要存儲空間，會造成頻繁的內存申請和釋放.

通過使用內存池的方法，可以有效提升內存空間的復用率，減少內存空間占用.同時避免了變換產生的臨時變量頻繁的申請和釋放,可以有效節省內存開銷，提升內存使用率，避免無用的時間浪費.

3.5 網絡規模裁剪

由于卷積神經網絡的計算復雜度和存儲空間與圖像的大小成正比，但是卷積神經網絡的輸入規模配置經常和圖像大小不一致，產生了一部分的計算冗余、資源浪費.在預處理時，很多圖像都有一定的比例，這與神經網絡的輸入不一致.特別是在處理攝像機或者視頻時，比例通常是16∶9，多余的部分必須填充到黑色區域，這樣會產生很多無用的計算，修改網絡的輸入大小，以適應16∶9的大小，可以有效地提高數據利用率和網絡速度.

3.6 16 b浮點量化

16 b浮點是指2 B大小的浮點類型.相對于32 b浮點，精度有效位數只有3或4位左右.對于卷積神經網絡，訓練使用16 b浮點會導致訓練效果下降，甚至得不到理想的模型.但對于經過32 b訓練出來的網絡模型，削減精度使用16 b的結果，與32 b的輸出效果相差不大，也避免了模型重新訓練、開發、轉換的問題.

隨著加速設備的發展和迭代，支持16 b浮點的硬件設備已經越來越多.使用16 b浮點來代替32 b單精度浮點進行計算，能有效保證浮點精度避免定點化帶來的精讀損失.同時對比32 b的單精度浮點，可以減少50%的內存空間并提升訪存效率.對于支持16 b浮點計算的硬件設備來說，可以提升計算效率.

4 實驗結果與分析

實驗測試的硬件平臺包括AMD V1605B APU與英偉達嵌入式GPU SOC TX2.AMD V1605B APU含有一塊Ryzen 嵌入式V1000系列CPU，主頻2.0 GHz，最大可達3.6 GHz主頻，以及1片Vega 8 GPU，有8個CU；TX2是一塊嵌入式SOC，包含雙核 Denver 2 64 位 CPU 和4核 ARM A57 Complex，以及1片NVIDIA PascalTM架構GPU，配有 256個NVIDIA CUDA核心.

實驗測試的對照軟件包括MIOpenGEMM，CLBlas，CLBlast，darknet采用的操作系統是Ubuntu 18.04.3，驅動為AMD官方Vega顯卡驅動.

4.1 GEMM算法對比

除了本文提出的GEMM算法，還對比測試了多種基于OpenCL的GEMM算法，包括MIOpen-GEMM，CLBlas，CLBlast.其中gemm0和xgemm都是來自MIOpenGEMM的GEMM實現.差別在于是否適用額外的矩陣變換.測試如圖6所示:

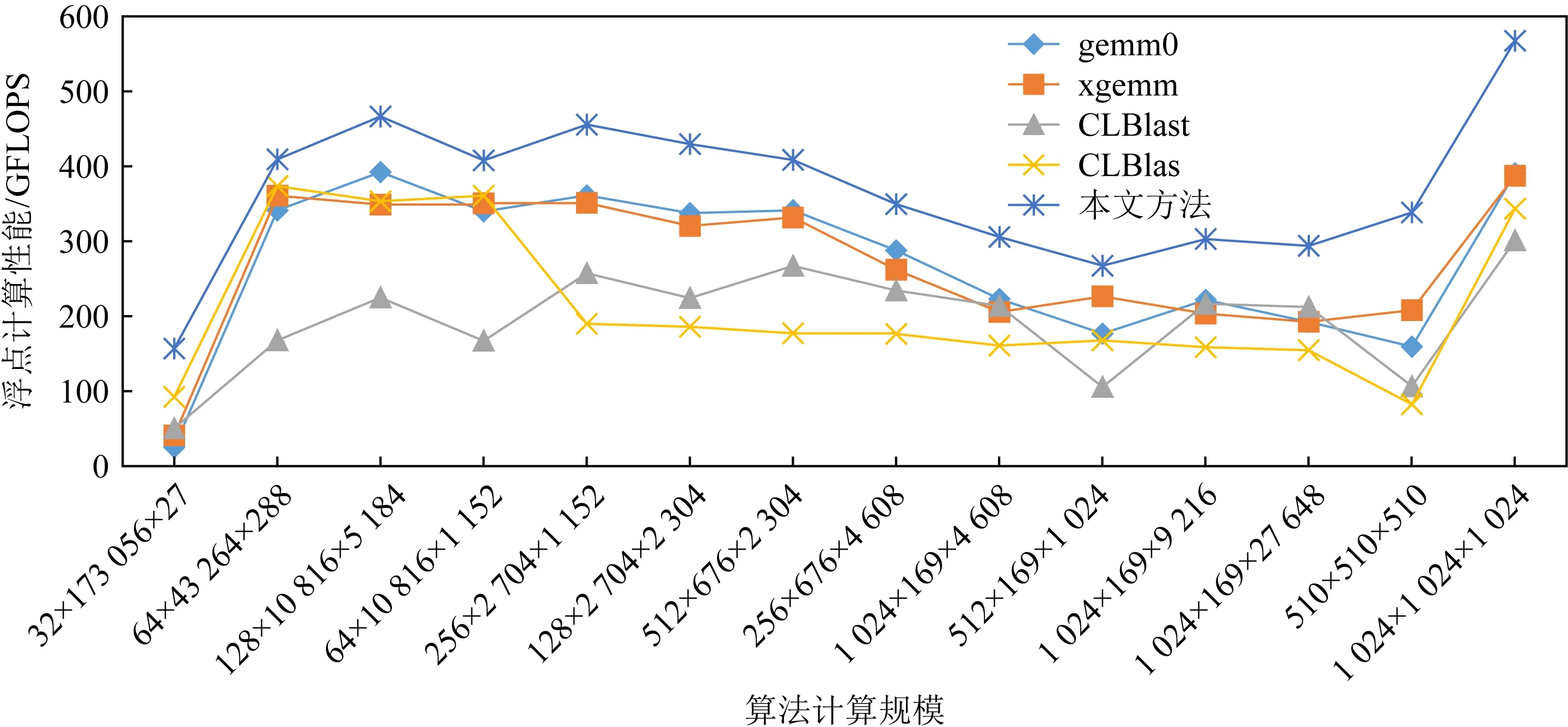
Fig. 6 GEMM algorithm performance test圖6 GEMM算法性能測試

從對GEMM算法的對比測試可以看出，深度卷積神經網絡中使用的卷積轉換成GEMM以后，這些規模的計算效率在當前的各個軟件算法庫中性能表現都遠低于1 024×1 024×1 024這種方形矩陣乘法的計算效率,而我們的方法針對于卷積神經網絡中的規模能夠有效地提升效率；同時對于1 024×1 024×1 024這種矩陣乘法，也有顯著的計算效率提升.

4.2 GEMM和Winograd實現卷積效率對比

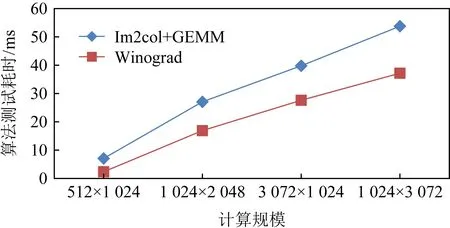
Fig. 7 Winograd algorithm performance test圖7 Winograd算法性能測試

對Winograd算法進行測試，結果如圖7所示.在進行GEMM和Winograd對比時，因為Winograd的變換包含了對卷積核心的變換，因此在測試GEMM和Winograd的性能時，采用卷積的規模進行測試和比較，計時標準為耗時.即在測試時，分別測試使用Im2col+GEMM的性能以及Winograd完成卷積的性能.

測試時使用的數據輸入輸出都為13×13規模，變化輸入和輸出通道數進行測試.可以看出：GEMM耗時較長，而Winograd算法耗時較少.

4.3 神經網絡推理性能對比

通過對比和測試TX2上運行YOLOv3等網絡的效率(使用darknet框架與cuDNN軟件)和AMD V1605B上運行YOLOv3等網絡的效率(使用本文方法)，來對比對卷積神經網絡推理性能的加速情況，以及對比使用CLBlas實現GEMM的效率，和本文實現的FP32和FP16(16 b量化)的效率.對于卷積神經網絡中滿足Winograd算法使用條件的，本文都采用了Winograd算法進行實現.測試結果如表2所示：

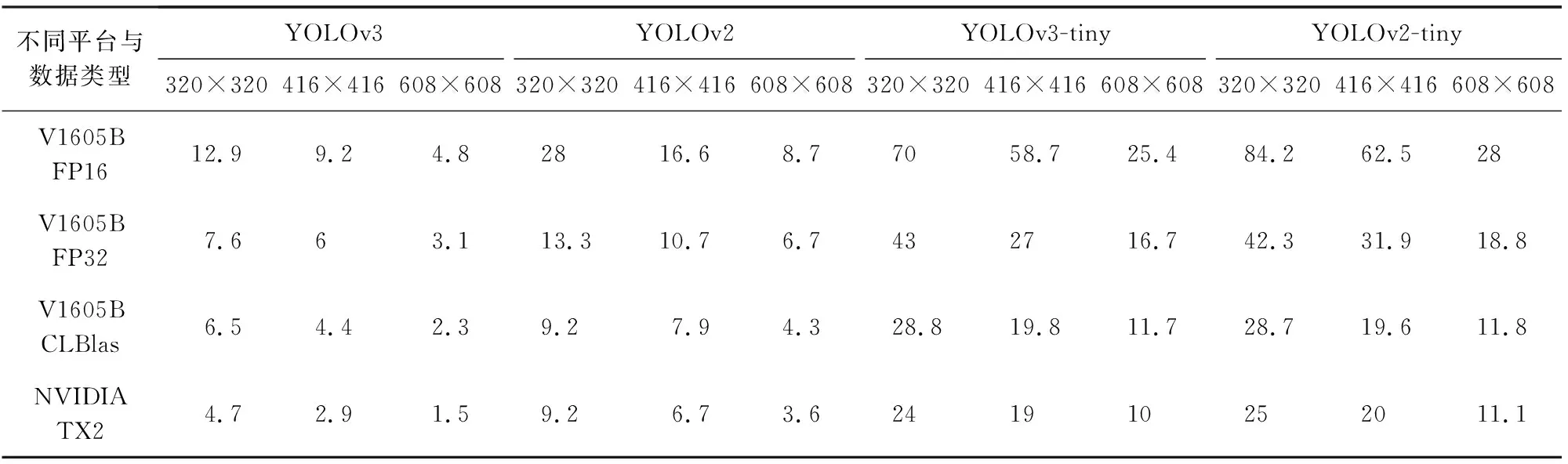
Table 2 Neural Network Inference Performance Test表2 神經網絡推理性能測試

5 結束語

本文以現有的GEMM算法在卷積神經網絡應用中的不足為出發點，有針對性地分析、加速GEMM算法.并以本文優化后的GEMM算法為基礎，實現了Winograd算法，并通過Winograd算法進一步對卷積進行加速.還提出了基于OpenCL的卷積神經網絡優化框架，借助優化后生成的GEMM算法自調優、16 b量化等，從框架上對卷積神經網絡進行了進一步的加速.最終通過實現和對比，測試了我們的加速方法是有效且高效的.

本文中對于GEMM算法生成了較多的實現，并結合遍歷的方法來進行自調優選擇了最優的實現方法.但是仍舊存在著一些不足，采用遍歷的方法相對較慢，沒辦法快速地找到效率最高的算法實現，有待進一步研究.

作者貢獻聲明：李茂文負責方法的設計與實驗實現，以及文章整體架構設計、撰寫和修改；曲國遠負責全文結構設計與指導，以及各章節內容撰寫；魏大洲負責數據的整理、校對和分析；賈海鵬負責部分設計的整理以及全文總結.