基于響應面的焊接件加肋板結構參數優化設計

周鑫

（中國直升機設計研究所，江西景德鎮 333001）

0.引言

焊接件加肋板結構在直升機強度試驗中是一種常見的結構形式，加肋板的焊接件在承載過程中能夠提高結構的承載能力以及結構的剛度，并且能夠提高結構的固有頻率，降低其振動響應等[1-2]。焊接件加肋板結構的承載能力很大程度上取決于肋板的結構參數以及布置位置，不合理的加肋板結構固然能保證結構的強度要求，但是也引起結構用鋼量較大，增加了制造成本，因此優化肋板的結構參數是有必要的[3]。

傳統的優化方法是根據經驗以及有限元分析對結構進行加強或者對材料冗余部位進行削減，傳統方法需要反復驗證從而造成效率較低并且改進的結構的最優性難以保證。隨著計算機的發展，多目標優化設計方法在機械設計領域中得到長足的發展，并且不斷發展出遺傳優化算法，神經網絡算法以及粒子群算法等用于求解復雜的、帶有約束的多目標優化問題。基于響應面法的多目標優化設計避免了試驗周期長，試驗結果對真實結果擬合誤差大的缺點[4]。

本文以焊接結構件為研究對象，在ANSYS中進行參數建模，然后進行靜力學分析，根據應力、變形及質量情況，采用Design Xplorer模塊對焊接件肋板的結構參數進行優化。

1.模型建立

本文利用ANSYS軟件Design Modeler模塊進行參數化建模，模型如圖1所示。肋板的結構參數表示如圖2所示。

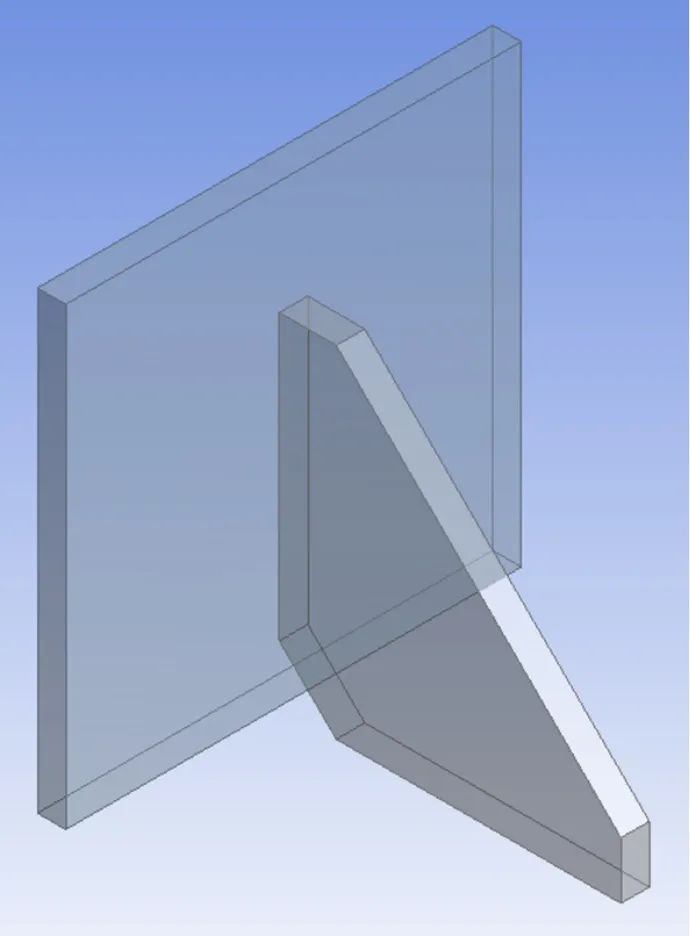
圖1 加肋板結構

圖2 肋板結構參數

將帶參數的肋板結構三維模型導入靜力學分析模塊，進行相關參數設置和靜力學分析。材料設置為結構鋼，密度為7850kg/m3，彈性模量為200Gpa，泊松比0.3。網格設置為六面體網格，網格單元尺寸為1mm，節點數73222，網格數量47728。實際狀態下肋板與立板的連接方式為焊接，為簡化模型設置兩接觸面之間用綁定接觸代替。立板背面施加在沿肋板長度的載荷，邊界條件為立板底面和肋板底面設置為固定約束。根據上述加載及邊界條件，求解得到等效應力和變形云圖，另外為避免應力奇異現象出現，在不影響肋板結構的情況下對存在的尖角進行圓角處理，求解結果如圖3和圖4所示。

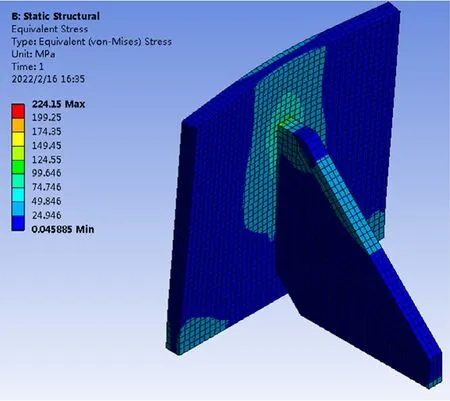
圖3 加肋板結構應力云圖

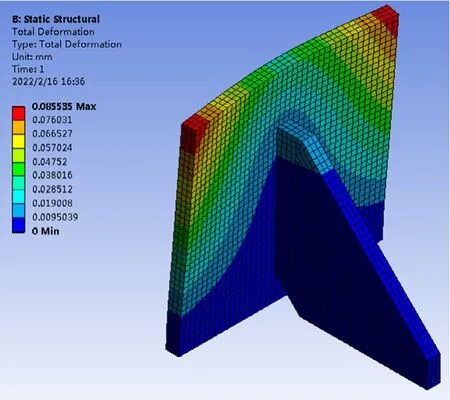
圖4 加肋板結構變形云圖

2.優化設計

優化設計的本質是將實際的工程問題轉化為數學問題，基于響應面的多目標優化設計是根據所設置的邊界條件及外部載荷建立數學模型，并在設計變量范圍內生成樣本點，通過樣本點計算響應面，對響應面上的設計點經過多次迭代，從而得到目標函數極值[5]。根據所求的極值，結合實際工程情況對比優化結果，從而產生符合要求的最優解。本文中優化設計的目的是在保證結構的強度和剛度情況下，實現結構的輕量化。設計變量為肋板長度L1，肋板高度H1，倒角長度L2，上緣長度L3，倒角高度H2，右緣高度H3，肋板厚度t，目標函數是使得該結構的強度和剛度最大并且材料最少，可等效為最大等效應力和最大變形最小，質量最小，對優化肋板結構的數學模型如下[6-7]：

其中 xi（i=1，2，3）是狀態變量，Hi、Li（i=1，2，3）和t是設計變量。

在進行優化設計前應進行相關參數的敏感性分析，敏感性分析的作用是確定輸入輸出參數對結構件尺寸的影響程度，得到輸入輸出參數的敏感性分析結果后，能夠直接找到對目標函數影響最為顯著的輸入參數，首先對影響顯著的參數作為優化對象，這可以使得優化過程中的優化參數數量的減少，降低了運算量和運算時間成本[8]。相關參數的敏感性分析結果如圖5所示，根據敏感性分析結果可知各個輸入參數對優化變量的影響程度不同，其中肋板高度H1對加肋板結構的質量、強度和剛度變量影響較為顯著分別達到了0.33、-0.89和-0.86；肋板厚度t對質量和應力影響較為顯著，其值分別達到了0.81、-0.30和-0.40；而肋板長度L1只對結構的質量和變形影響較大，對應力影響較小；上緣長度L3對質量和應力影響較大。另外，敏感性分析結果顯示的影響趨勢也是符合預期的。

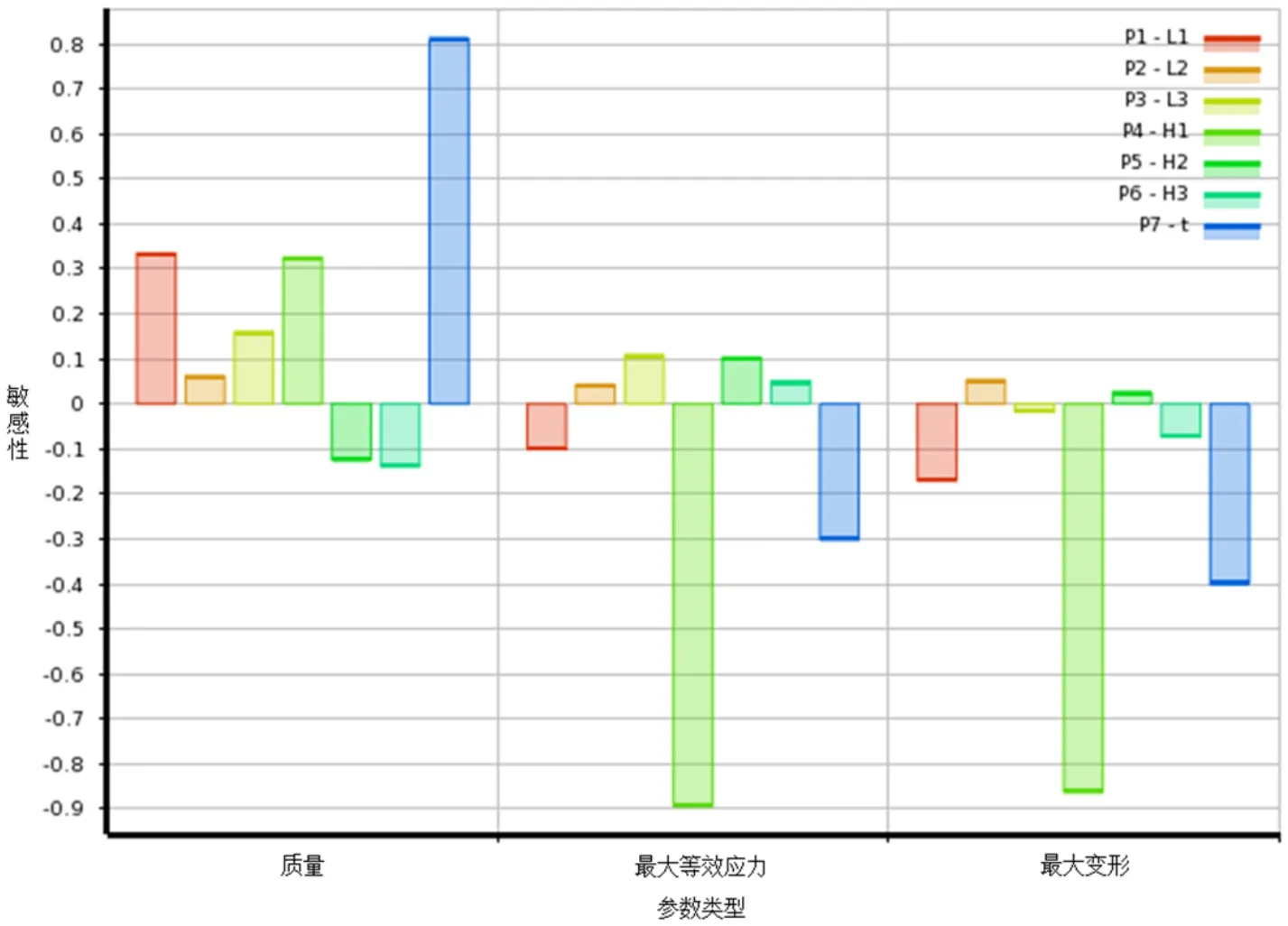
圖5 肋板結構參數敏感性分析

響應面的構造應該先生成試驗點，而試驗點的選取對響應面的精度有很大的影響，試驗點選擇不合理有可能造成響應面無法擬合。目前的試驗點的設計方法主要有Central Composite Design（CCD）、Optimal Space-Filling Design（OSF）、Box-Behnken Design（BBD）等，本文采用OSF方法生成試驗點。常見構造響應面的模型主要有Genetic Aggregation、標準響應面、Kriging、非參數回歸（Non-parametric Regression）和神經網絡模型[9]，本文選擇Kriging模型構造響應面，該類型的響應面模型適合非線性參數模型。響應面模型的擬合程度直接影響著后續優化結果的準確性，評估響應面準確性的參數指標主要是決定系數R2、均根方差RMSE，相對平均絕對誤差RAAE。依據圖6所示響應面的預測值與計算值之間的偏差，可以發現局部誤差較大區域并對該區域進行細化，經過兩次添加驗證點細化，Kriging模型建立的響應面具備相應的精度，其評估參數如表1所示。

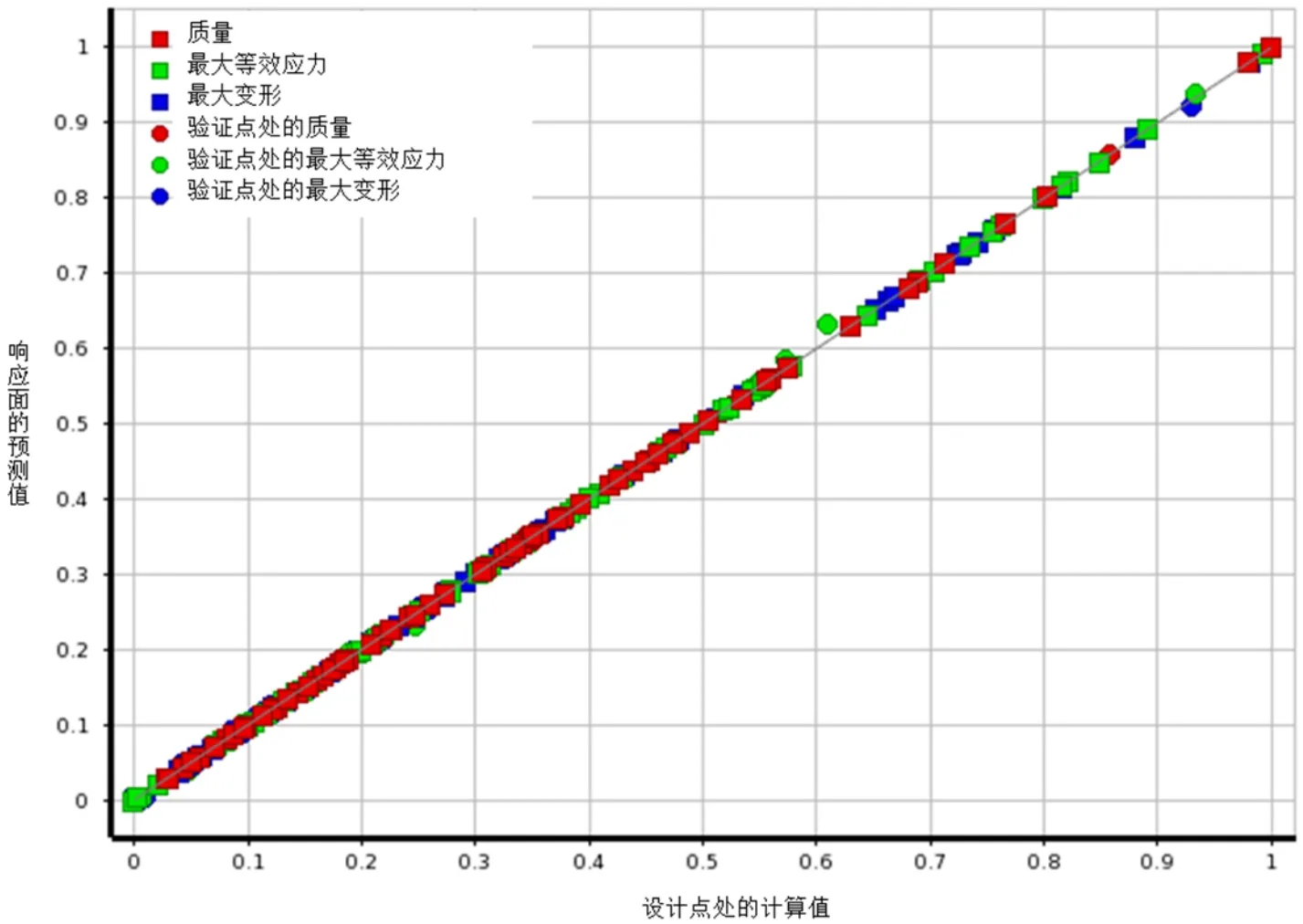
圖6 響應面設計點處計算值與響應面預測值的偏差

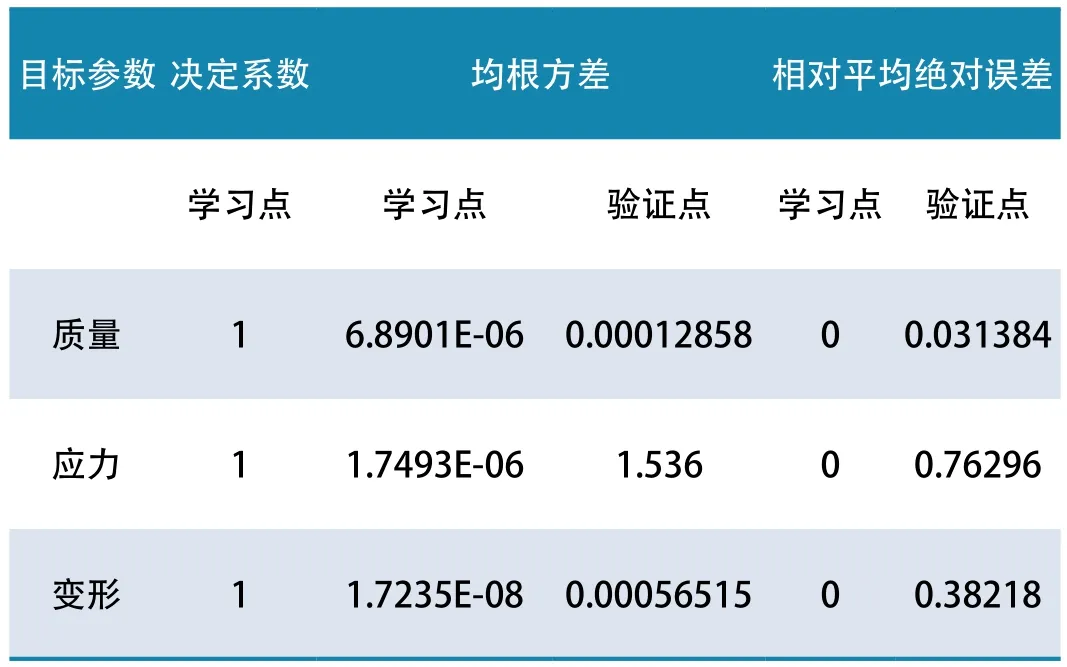
表1 Kriging模型評估

3.優化設計結果

根據對肋板結構參數敏感性的分析，肋板高度H1，肋板長度L1，上緣長度L3和肋板厚度t對狀態變量質量、強度和剛度影響較為顯著，故對該四類參數進行響應面分析，響應面分析結果如圖7～圖10所示。

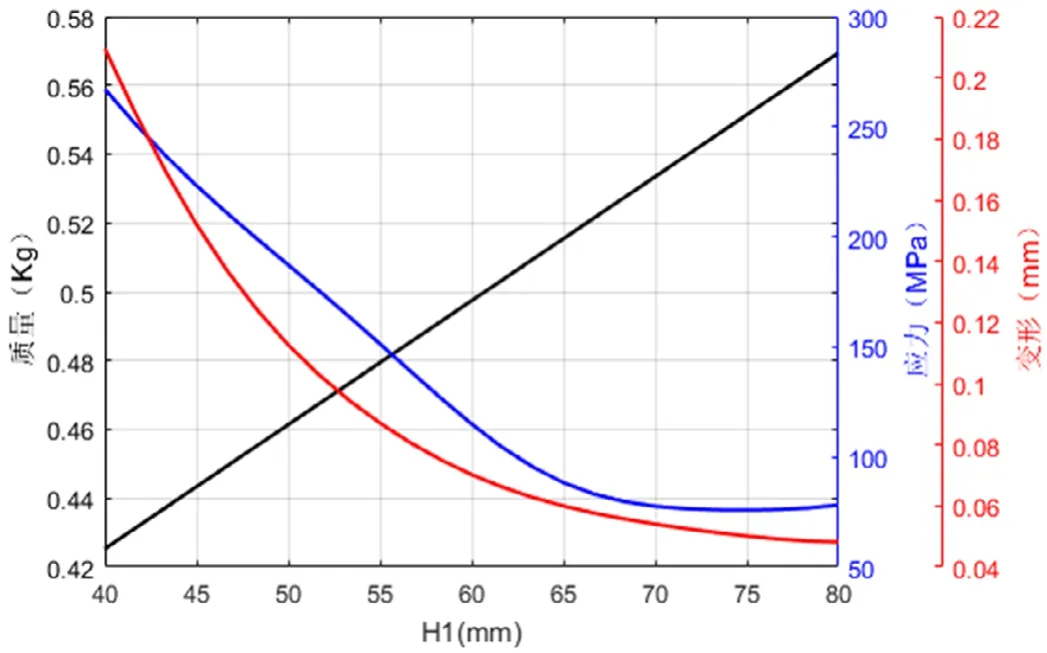
圖7 肋板高度H1對質量、應力和變形的影響

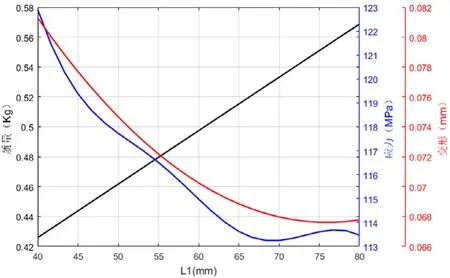
圖8 肋板長度L1對質量、應力和變形的影響

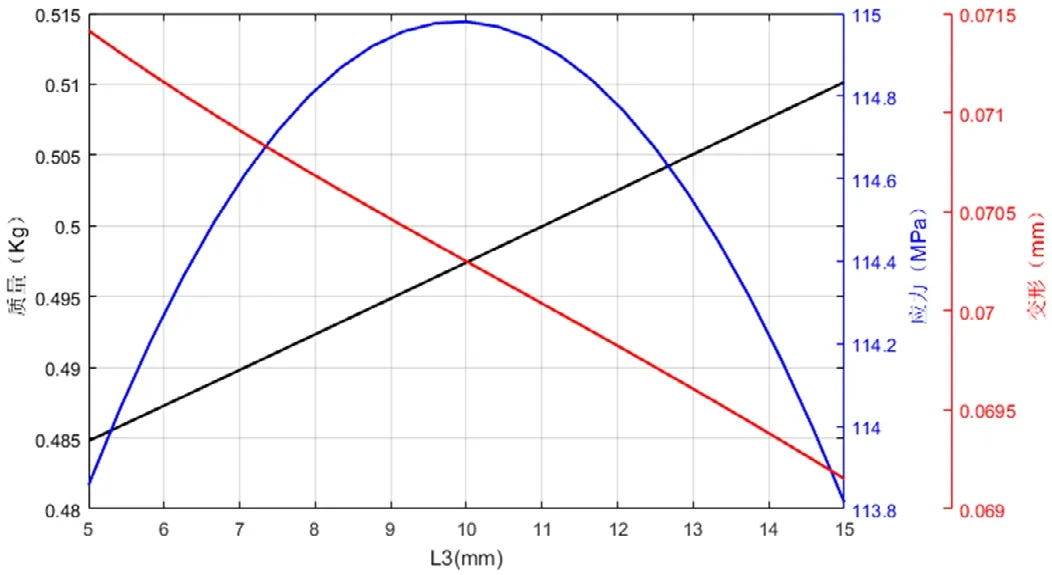
圖9 右緣高度L3對質量、應力和變形的影響

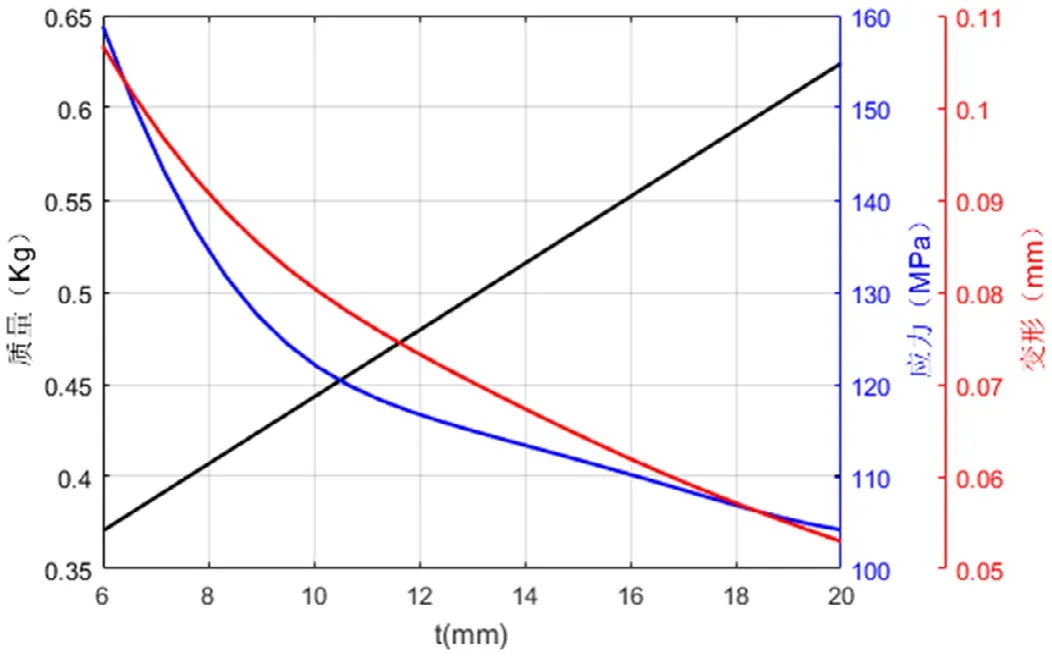
圖10 肋板厚度t對質量、應力和變形的影響

從圖上可以看出，該結構的質量參數與其尺寸參數成正比，這和預期的結果是一致的。最大變形量基本上是隨著結構尺寸參數的增大而減小，表明其剛度隨著尺寸增大而增加，但是各個結構尺寸參數對變形量的影響程度均不相同，H1、L1和t影響程度基本上呈現出逐漸減少的趨勢，值得注意的是L3和最大變形量之間存在極強的線性關系。最大等效應力隨著肋板長度、高度與厚度參數增加而較小，并且其對最大應力的影響程度隨著尺寸參數的增加而降低。另外值得注意的是隨著L3的增加最大等效應力呈現出先增大后減小的拋物線趨勢，并且在10mm附近出現極大值點。

基于Kriging建立的響應面模型，設定約束目標為質量最小，最大等效應力最小和最大變形最小。優化方法采用MOGA，初始迭代數目設定為4000，迭代20次，每次迭代數量為800。如圖11所示為經過20次迭代獲得的質量與最大等效應力的帕累托解，使用篩選算法可以生成3個備選設計點，如表2所示。3個備選設計點在質量，最大等效應力和最大變形方面相差不大，根據本文擬定的優化目標是材料用料最少，即結構尺寸最小，且承載能力最高、變形最小，故在滿足強度的情況下選擇質量最小的設計點即樣本點6。樣本點6結構尺寸在質量減少8.7%的情況下，強度提高了15.3%，剛度提高了8.8%。另外，發現肋板高長比在1.3～1.5，肋板上緣長度5mm～6mm，肋板厚度在7mm～8mm范圍內對減少材料用料提高結構強度方面較為合理。

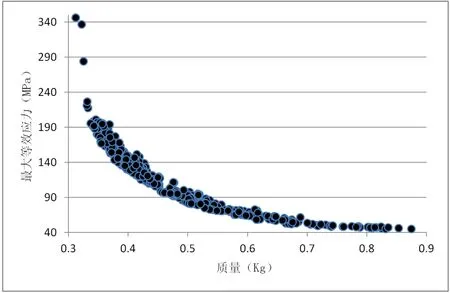
圖11 質量與最大等效應力的帕累托解

表2 備選設計點

4.結論

本文介紹了直升機強度試驗過程中焊接件加肋板結構參數優化方法，基于Kriging模型建立響應面，采用多目標遺傳算法MOGA對目標參數進行優化獲得優化后的結構參數。在敏感性分析過程中，對性能目標影響顯著的主要是肋板長度、高度、上緣長度和肋板厚度參數，對該四種參數進行優化分析過程中發現上緣長度與應力呈現拋物線形式，并且在L3=10mm附近存在極大值點。另外，各參數對強度影響顯著性隨著結構尺寸的增大而逐漸減少。最后，結構尺寸在質量減少8.2%的情況下，強度提高了16.3%，剛度提高了11.3%，對所生成的備選設計點分析，合理的肋板高長比在1.3～1.5，合理的肋板上緣長度≈5mm，而肋板厚度在7mm～8mm范圍內較為合理。