基于改進粒子群算法的并網逆變器分數階PIλDμ控制研究

謝玲玲，陸柳，劉斌

(廣西大學 電氣工程學院，南寧 530004)

0 引 言

絕大多數的可再生能源是以逆變器作為并網接口，并網逆變器是可再生能源發電單元、公共電網以及本地負載之間的能量轉換接口裝置，承擔著分布式發電(Distributed Generation，DG)系統能量的轉換與控制，其性能好壞直接決定著并網電流質量，對DG的安全、穩定和高質量運行十分重要[1]。LCL濾波器為三階系統，存在高頻諧振峰，將其應用于并網逆變器電流濾波時，該諧振峰容易導致逆變器系統失穩。當電網發生擾動時，采用整數階PID控制器的并網逆變器抑制電網諧波的能力不足，降低電能質量[2-3]。因此，為提高并網逆變器系統的諧波抑制能力，增強穩定性和快速動態調節能力，研究并網逆變器高效可靠的控制策略具有重要的理論和實際工程意義。

整數階PID控制器結構簡單，易于操作，在并網逆變器控制中得到了廣泛的應用。文獻[4]提出了一種電壓型逆變器自適應PID控制方法，通過在傳統PID控制基礎上，增加3個控制項來提高系統魯棒性，但該自適應控制方法對系統增益的調整有限，同時增加了系統設計的復雜性。文獻[5-6]在PID控制方法的基礎上提出自適應比例諧振微分(PRD)控制方法，實現了對參考信號的零穩態誤差跟蹤，提高了系統的動態響應性能，改善了并網電能質量，通過對傳統整數階PID控制方法進行改進，在一定程度上改善了系統性能，但因參數選擇的局限性，PID控制器的穩定范圍仍受限，致使控制系統性能欠佳。

隨著非線性控制理論的迅速發展，非線性控制方法在電力電子變換器中的應用愈加廣泛。Podlubny教授在1999年提出了分數階PIλDμ控制器，在傳統PID控制器的基礎上引入了兩個可調參數：積分階次λ、微分階次μ，與整數階PID控制器相比，分數階PIλDμ控制器的控制效果更具柔性，控制范圍也從點狀網格擴展到面狀[7-9]。目前分數階PIλDμ控制已在化工、電力、機械、自動化等領域中得到了應用。文獻[10-12]給出了分數階PIλDμ控制器的設計方法及其參數整定方法，將該控制器應用于簡單控制系統中，并與傳統整數階PID控制效果進行比較，結果表明分數階PIλDμ控制器能獲得比傳統PID控制器更快速的動態響應，其控制效果更顯著。文獻[13-14]針對光伏并網逆變器及其最大功率點追蹤，提出并設計一種基于能量整形的無源分數階PIλDμ控制器，算例仿真結果表明，該控制器在各種大氣條件下均能獲得最滿意的控制性能，且總體控制成本最低。

提出一種基于改進粒子群算法(Modified Particle Swarm Optimization Algorithm，MPSO)的并網逆變器分數階PIλDμ控制策略，相比于傳統PID控制器，PIλDμ控制器的可調參數變多，可更加靈活地控制被控對象。粒子群算法經改進后可進一步提高局部搜索收斂速度，使控制器參數尋優的效率與精度更高。文章首先分析分數階PIλDμ控制器參數λ、μ對被控系統穩定性的影響；其次建立并網逆變器數學模型，在此基礎上提出基于分數階PIλDμ控制器的并網逆變器控制策略，并與整數階PID控制進行比較；最后采用MPSO算法對分數階PIλDμ控制器進行參數尋優，使參數隨外界環境的變化而自動調整。仿真結果驗證了理論分析的正確性。

1 分數階PIλDμ控制器

分數階PIλDμ控制器結構框圖如圖1所示。其中，Kp為比例系數，Ki為積分系數，Kd為微分系數，λ為積分階次，μ為微分階次。

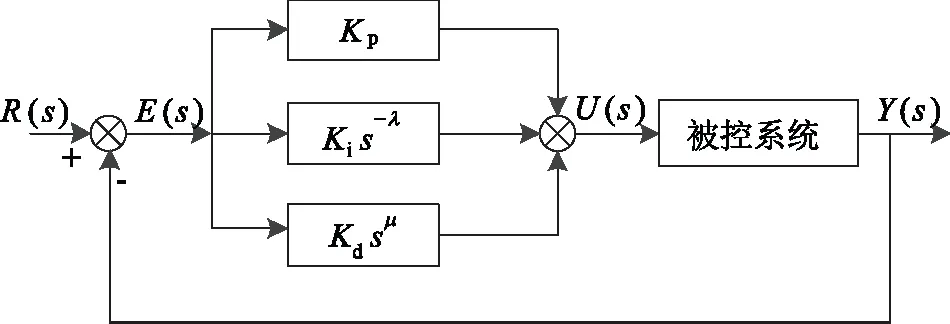
圖1 分數階PIλDμ控制系統結構框圖

由圖1可得，分數階PIλDμ控制器的傳遞函數為：

(1)

式中 積分階次λ與微分階次μ分別滿足0<λ<2、 0<μ<2。時域下，控制器輸出U(s)表達式為：

u(t)=Kpe(t)+KiD-λe(t)+KdD-μe(t)

(2)

由式(1)、式(2)可知，當λ=μ=0時，為P控制器；當λ=1,μ=0時，為PI控制器；當λ=0,μ=1時，為PD控制器；λ=μ=1時，為PID控制器。

引入積分階次λ和微分階次μ使得分數階PIλDμ控制器參數的取值更加靈活多變。圖2所為控制系統在不同積分、微分階次下的伯德圖。

由圖2可知通過改變分數階PIλDμ控制器中的積分階次λ和微分階次μ的值可改善系統的穩態誤差與動態特性。

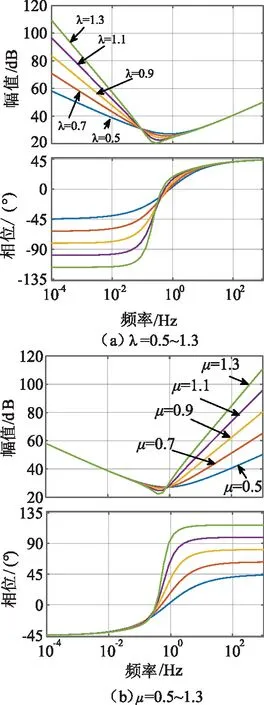
圖2 不同積分、微分階次下的伯德圖

2 基于分數階PIλDμ控制的單相LCL并網逆變器系統

2.1 并網逆變器系統數學模型

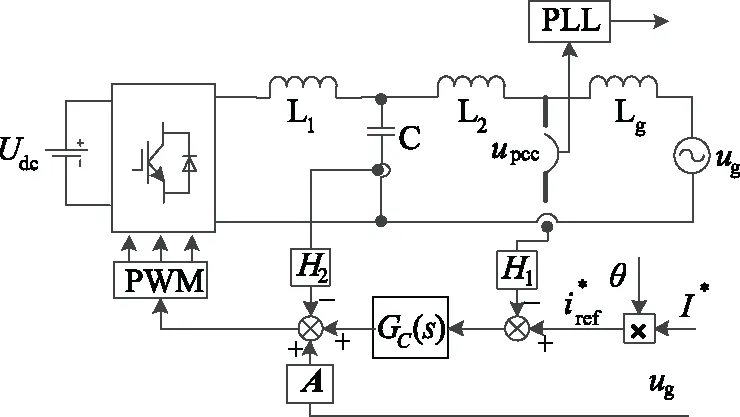
圖3 系統控制示意圖

并網逆變器系統控制框圖如圖4所示。當開關頻率足夠高時，逆變橋等效為比例環節，Kpwm=Udc/Uca，其中Uca為三角載波的幅值。

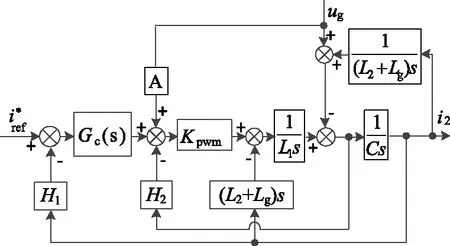
圖4 系統控制策略框圖

D1(s)=H1KpwmGC(s)+(L1+L2+Lg)s+

H2C(L2+Lg)Kpwns2+CL1(L2+Lg)s3

(3)

(4)

在只考慮ug輸入的情況下，系統的傳遞函數為：

(5)

則系統輸出并網電流i2的表達式為：

(6)

因此，要使并網電流不受電網電壓影響，應滿足：

G2(s)ug(s)=0

(7)

將式(5)代入式(7)得傳遞函數A的表達式為：

(8)

當A滿足式(7)時，系統可完全消除電網電壓對并網電流的影響。

2.2 并網逆變器系統穩定性分析

整數階PID控制的系統具有有限維的特點，而分數階系統可實現無限維控制，因此直接求解分數階微積分方程具有較大的困難[15]。采用改進型Oustaloup濾波算法對分數階微分算子進行擬合。改進的Oustaloup濾波器的數學模型為[16]：

(9)

式(9)中相關變量的說明如下：

(10)

式中ωh為劃定頻段上限；ωb為劃定頻段下限；b=10,d=9。

由圖4可得系統開環傳遞函數為：

(11)

當系統控制器為整數階PID時，Gc(s)為PID控制器傳遞函數；當系統控制器為分數階PIλDμ時，Gc(s)為PIλDμ控制器傳遞函數。由式(9)可得系統采用整數階PID與分數階PIλDμ控制器的伯德圖如圖5所示。

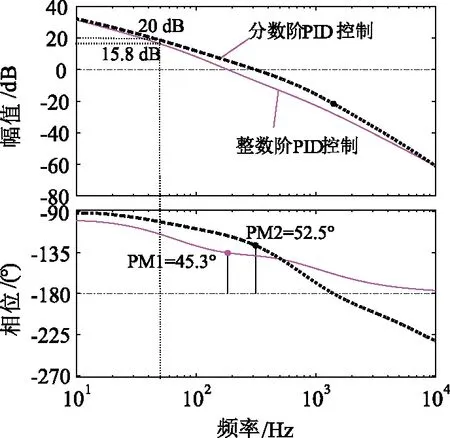
圖5 不同控制策略下的系統伯德圖

由圖5可知，采用整數階PID控制時系統在基頻處的增益為15.8 dB，系統相位裕度為45.3°；當采用分數階PIλDμ控制時，系統在基頻處的增益為20 dB，系統相位裕度提高到了52.5°，分數階PIλDμ控制時，系統基頻增益與相位裕度均有所提高，且系統在高頻段對諧波的衰減能力更強。顯然，系統在采用分數階PIλDμ控制時，其動態響應速度與諧波衰減能力均有所改善。

3 基于分數階PIλDμ控制器參數取值范圍與尋優

3.1 Ki與λ的取值范圍

當Kp=50、Kd=0.05、Ki=6 000、μ=0.9，λ從0.5變化到1.3時，開環系統奈氏圖如圖6所示。由圖6可以看出,當積分階次λ<1時，λ越大，系統相位裕度隨之增大；當λ>1時，λ的變化對系統穩定性幾乎無影響。

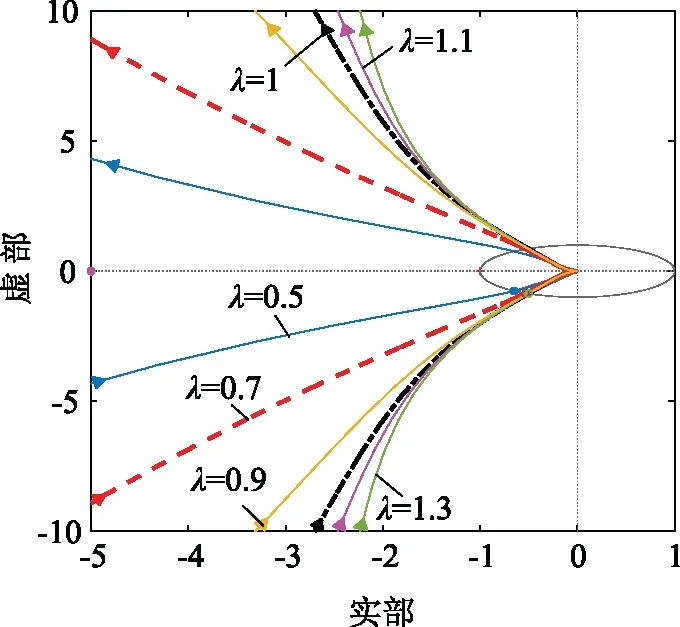
圖6 λ=0.5～1.3對應系統奈氏圖

當Kp=50、Kd=0.05、μ=0.9，λ從0.7變化到1.3，Ki從600變化到1 000時，開環系統的奈氏圖如圖7所示。

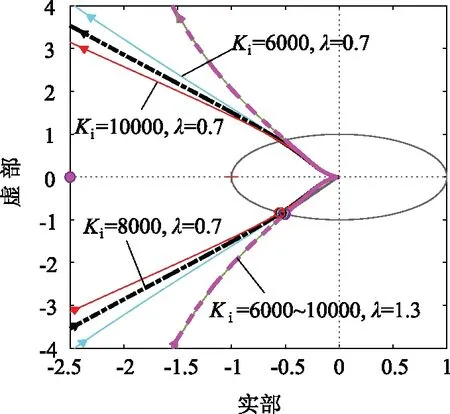
圖7 Ki=6000～10000, λ=0.7～1.3對應開環系統奈氏圖

由圖7可知，當λ<1時Ki越小，系統相位裕度隨之增大，但仍小于40°；當λ>1時，Ki的變化對系統穩定性幾乎無影響。為保證系統相位裕度γ>40°，應選取1<λ<2；Ki的值可根據實際情況選取。

3.2 Kp、Kd與μ的取值范圍

文中所研究的單相LCL并網逆變器系統為Ⅱ型系統，當μ>1時，開環系統在右半平面有一個極點，但開環系統奈氏曲線逆時針、順時針包圍(-1，j0)點各一圈，故閉環系統不穩定。當Kp=50、Kd=0.05，μ從0.5變化到1.3時開環系統奈氏圖如圖8所示。由圖8可知當μ<1時，隨著μ增大，系統相位裕度和增益裕度也會逐漸增大。

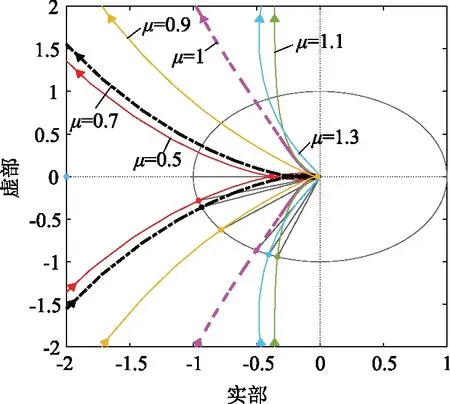
圖8 Kp= 50、Kd =0.05對應開環系統奈氏圖

當Ki=6 800、λ=1.3、μ=0.9，Kp從30變化到80，Kd從0.05變化到0.5時，開環系統奈氏圖如圖9所示。表1為μ=0.9時，Kp、Kd對應的系統相位裕度與增益裕度的值。

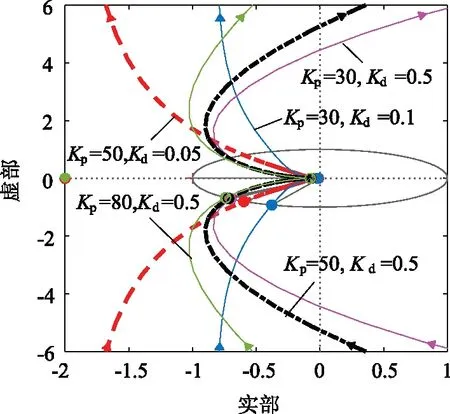
圖9 μ=0.9對應的開環系統奈氏圖

由圖9與表1數據可知，當Kp增大時，系統相位裕度與增益裕度均呈下降趨勢；當Kd從0.05增大到0.1時，相位裕度增加了14.5°，Kd繼續增大，相位裕度反而顯著下降，增益裕度則隨著Kd的增大持續下降。因此，為保證系統有足夠的穩定裕度，μ的取值應不大于1；Kp應不大于80，同時考慮到系統的魯棒性，Kd應不大于0.5。

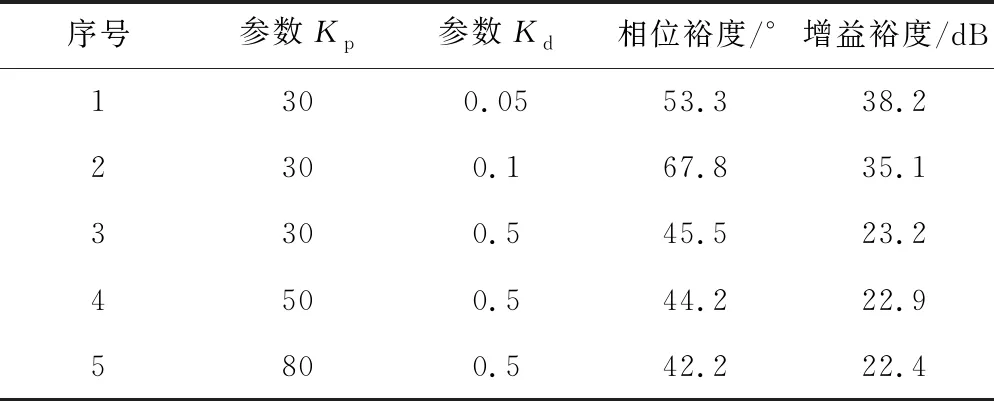
表1 μ=0.9時，Kp、Kd對應系統穩定裕度的值

3.3 基于改進粒子群算法的分數階PIλDμ控制器的參數尋優

為了克服手動調節參數的不確定性和繁瑣性，降低分數階控制器解析設計的復雜性，采用改進粒子群(Modified Particle Swarm Optimization, MPSO)算法對分數階PIλDμ控制器進行參數尋優，從而提高控制器參數的自適應性。

將分數階控制器PIλDμ的參數Kp、Ki、Kd、λ、μ作為1個粒子的5個維度，在五維空間中對參數進行尋優計算[17]。粒子i在第t+1次迭代計算時的速度和位置根據以下公式進行更新[18]：

Vin(t+1)=w(t+1)Vin(t)+c1r1(Pin(t)-Xin(t))+c2r2(Pgn(t)-Xin(t))

(12)

Xin(t+1)=Xin(t)+Vin(t+1)

(13)

式中Vin和Xin為第i個粒子的速度與位置。其中，1≤n≤N,N為搜索值域的維數，w為慣性權重，c1和c2為粒子加速系數，r1、r2是兩個獨立的隨機數，介于[0,1]之間，c1r1和c2r2控制整個粒子群的運動速度。Pi為第i個粒子當前的最佳位置，Pg為粒子群目前的最佳位置。Xin∈[Xmin，Xmax]，粒子的取值范圍由當前具體問題決定，Vin∈[Vmin，Vmax]，單步前進最大速度Vmax是根據粒子的取值范圍來確定的，可以用來限制粒子單步迭代的最大速度。

為保證粒子群不陷入局部最優解，在每一次的迭代過程當中，都更新粒子群的動態。因此在基本粒子群算法上對粒子群的慣性權值進行改進，使其隨迭代次數的增加而線性下降，以實現在算法搜索前期能加強全局搜索能力，擴大搜索空間，而當算法迭代次數增多后，則縮小搜索范圍，圍繞粒子當前位置進行局部搜索，增強算法收斂性，提高算法精度。改進的慣性權值的計算公式為[19]:

(14)

式中w(k)為粒子群在第k代時的慣性權值；wmax、wmin分別代表權重取值區間的上、下限；t為當前所處進化代數，Iter為算法設定進化代數的上限。

在參數尋優過程中，選擇ITAE指標作為適應度函數[20]，e(t)為系統誤差，J的值越小表示系統控制性能越好：

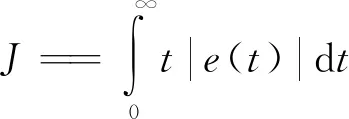
(15)

改進粒子群算法的流程如圖10、圖11所示。

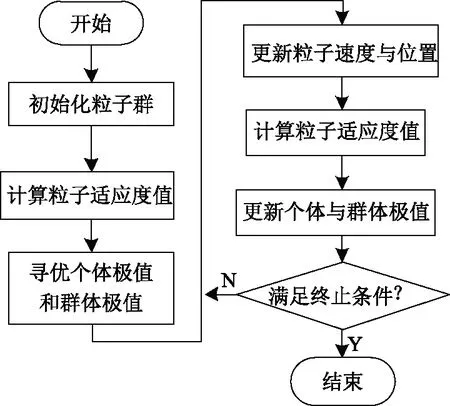
圖10 改進粒子群算法流程圖

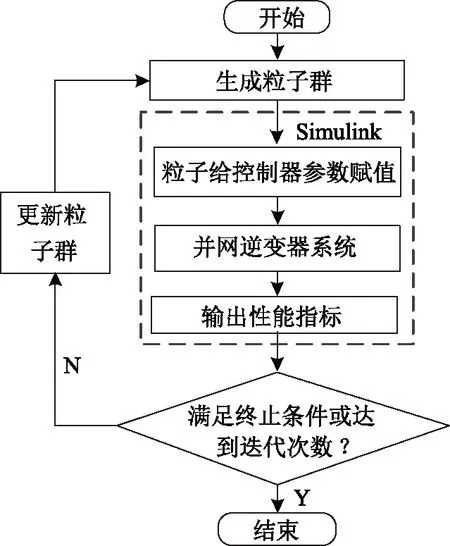
圖11 MPSO優化控制器流程圖

優化過程中，粒子和其所對應仿真模型的輸出值作為Simulink仿真模型與MPSO算法之間的橋梁。

使用MPSO算法優化分數階PIλDμ控制器的系統伯德圖如圖12所示，圖12中對應的系統各項指標如表2所示。

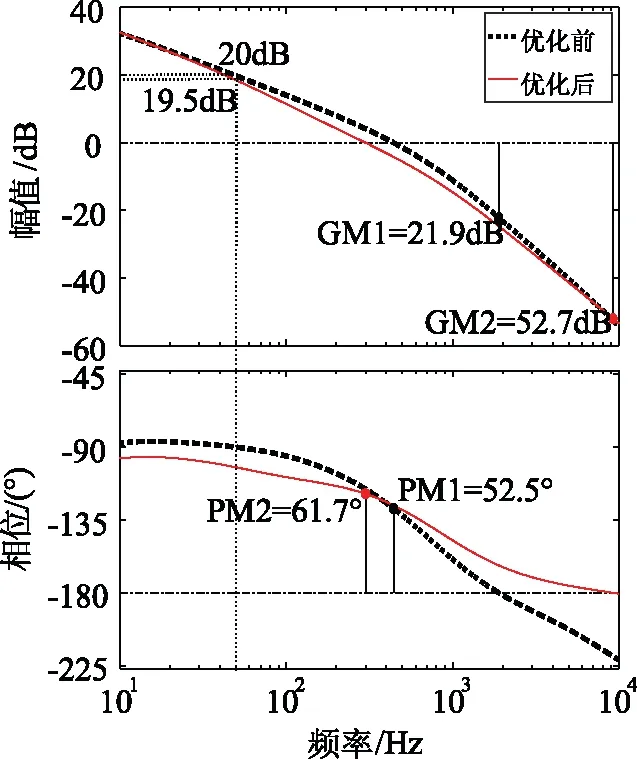
圖12 MPSO算法優化PIλDμ控制器的系統伯德圖

表2 MPSO算法優化分數階PIλDμ控制器前后系統各指標

由表2可知，使用MPSO算法優化分數階PIλDμ控制器，雖然系統的基頻增益下降了0.5 dB，但大大提高了系統增益裕度和相位裕度。因此，MPSO算法優化分數階PIλDμ控制器可改善系統動態與穩態性能。

4 仿真結果分析

為驗證上述控制方法的有效性，在Simulink平臺上搭建單相LCL并網逆變器系統模型。仿真參數如表3所示。

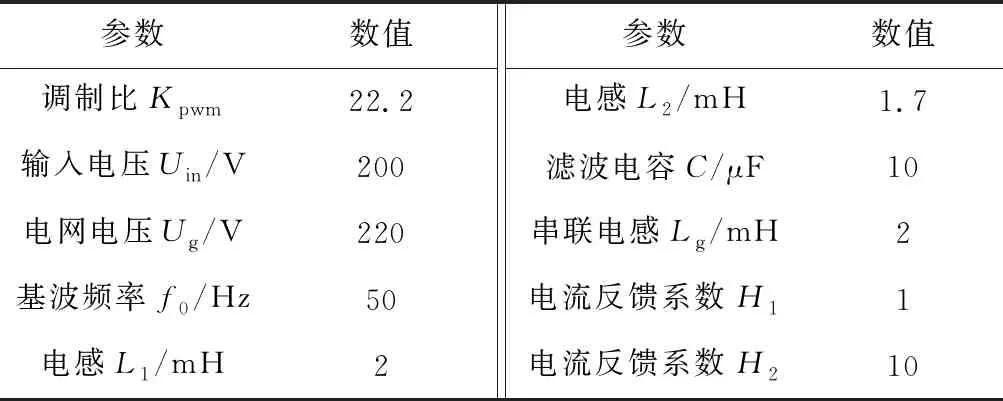
表3 仿真參數

在實際應用中，電網存在著一定量的高頻諧波，因此在仿真過程中向電網ug摻入11次、13次、15次諧波分量。

電網含11次、13次、15次諧波分量時仿真波形如圖13所示。可以看出，采用傳統整數階PID控制時，并網電流受電壓質量的影響較大，電流波形正弦性良好但卻不光滑，高次諧波含量較大；采用基于MPSO算法的分數階PIλDμ控制器時，并網電流波形正弦性好且光滑，更好地消除了電網中的諧波影響。

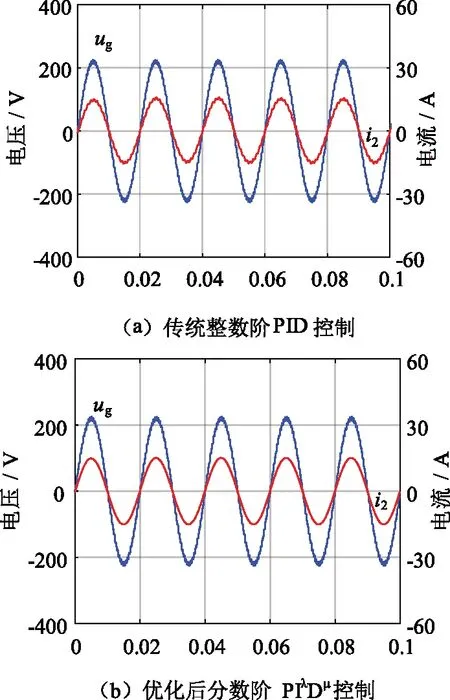
圖13 電網含11次、13次、15次諧波分量時仿真波形

不同控制下并網電流的諧波含量分析如圖14所示。

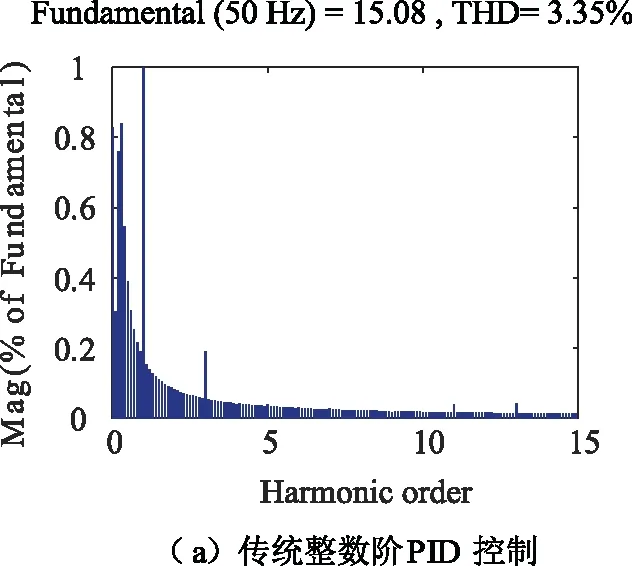
圖14 不同控制下并網電流的諧波含量分析

由圖14可知，傳統整數階PID控制下的并網電流諧波含量為3.35%，分數階PIλDμ控制下并網電流的諧波含量為0.49%，電流諧波含量明顯降低。

不同控制下電流突減仿真波形如圖15所示。從圖15(a)可知，傳統整數階PID控制下電流在0.04 s從15.08 A突減至7.08 A，經過0.002 1 s后電流恢復；從圖15(b)可知，分數階PIλDμ控制下電流在0.04 s從15.08 A突減至7.08 A，經過0.001 2 s后電流恢復穩定。

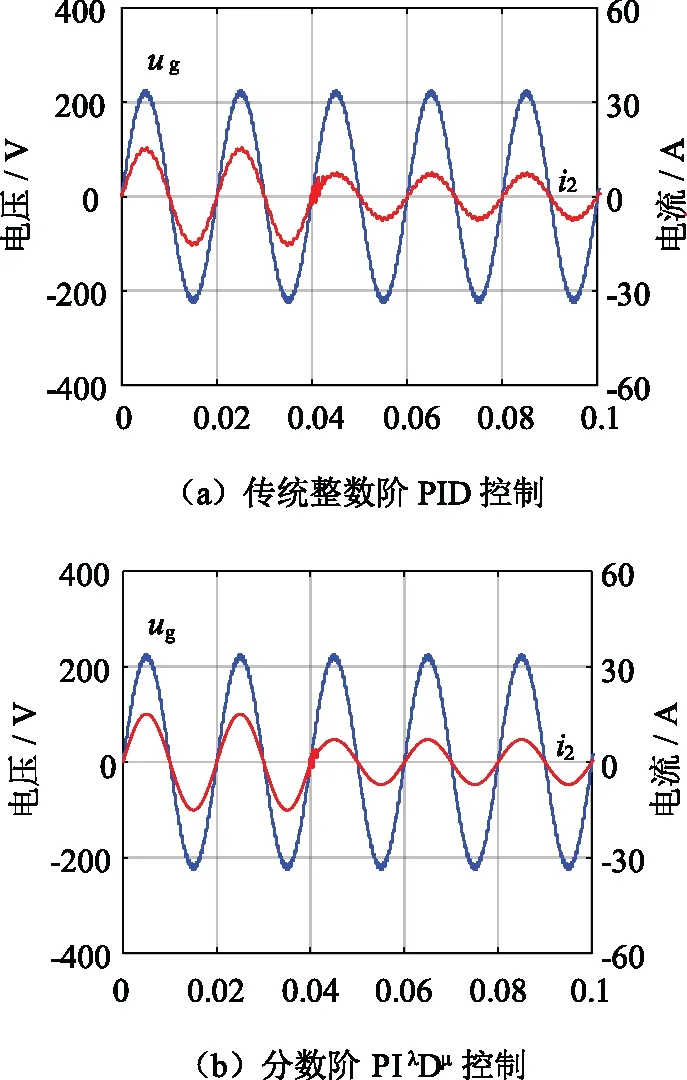
圖15 不同控制下電流突減仿真波形

不同控制下電流突增仿真波形如圖16所示。由圖16(a)可知，傳統整數階PID控制下電流在0.04 s從15.08 A突增至23.08 A，經過0.002 2 s后電流恢復；由圖16(b)可知，分數階PIλDμ控制下，電流在0.04 s從15.08 A突增至23.08 A，經過0.001 2 s后電流恢復穩定。分數階PIλDμ控制下電流突變時系統均能更快速的恢復穩定，因此采用分數階PIλDμ控制器，可大大提高并網逆變器動態響應。

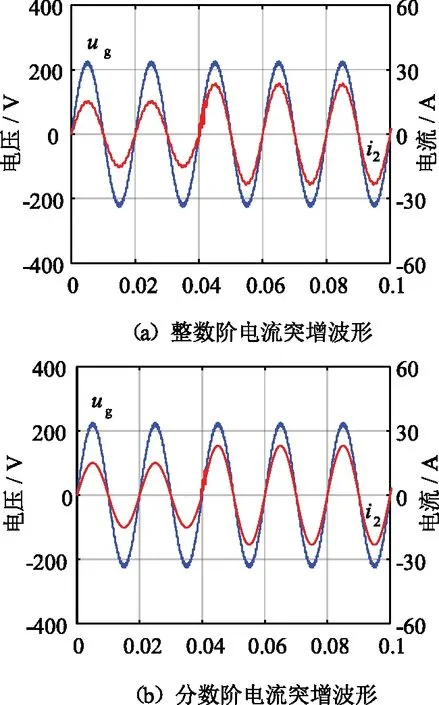
圖16 不同控制下電流突增仿真波形

以電網電壓突降作為外部擾動，分數階PIλDμ控制下，電網電壓在0.045 s時，電壓突降20%，從220 V跌落至176 V。外部擾動下入網電流的波形和諧波含量分析分別如圖17、圖18所示。

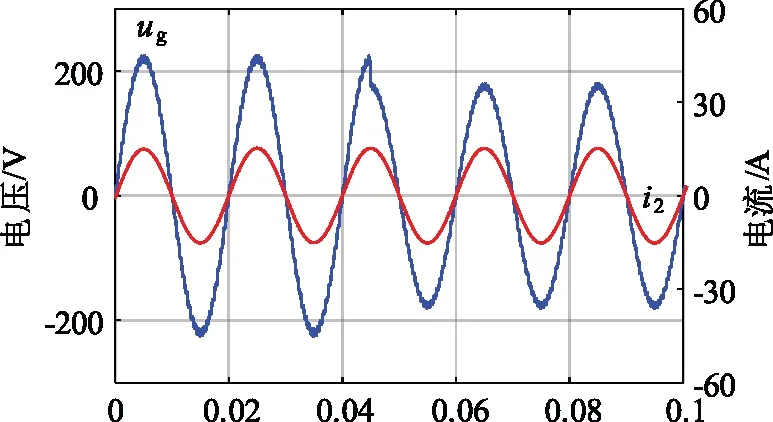
圖17 外部擾動下入網電流的波形

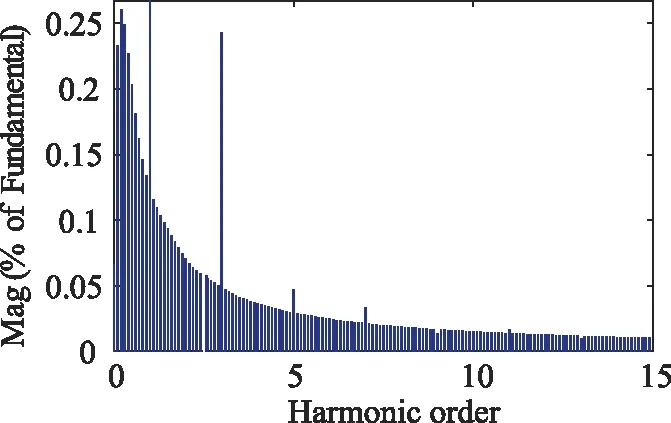
圖18 外部擾動下入網電流諧波含量分析

從圖17可知，入網電流波形良好，與圖12(b)對比無變化。

從圖18可知，在分數階PIλDμ控制下，入網電流THD值為0.67%，對比圖14(b)，THD值雖增加了0.18%，但仍在標準要求的范圍內，證明分數階PIλDμ控制能夠良好抑制電網電壓跌落、諧波等外部擾動。

5 結束語

文章對基于改進粒子群算法的單相LCL并網逆變器分數階PIλDμ控制系統進行了深入的研究，詳細分析了λ、μ對系統控制性能以及Kp、Ki、Kd穩定范圍的影響：當λ、μ≤1時，λ、μ增大時，Kd的穩定范圍與系統穩定裕度隨之增大，系統抗干擾性增強，但響應速度也隨之下降；相反，λ、μ減小時，系統相位裕度下降，若λ、μ的值過小，容易造成系統震蕩，甚至不穩定；當1<λ<2時，其值的變化對系統性能基本無影響，但當μ>1時，系統失穩。將分數階PIλDμ控制器與電流雙閉環、網壓前饋控制相結合，使得入網電流THD值下降到標準規定的0.5%以下，且系統受到外部擾動時，分數階PIλDμ控制能很好抑制干擾，仍可保證入網電流THD值低于1%，大大提高了電能質量。采用改進粒子群算法對分數階PIλDμ控制器進行參數整定，在控制過程中實現參數自動尋優，進一步提高系統的效率和控制性能。仿真驗證了所提控制策略的有效性。