例談挑戰性學習任務在小學數學教學中的運用

山東省威海市第二實驗小學 夏建華

《義務教育數學課程標準 (2011 年版)》中提出:學生的數學學習內容應當是現實的、有意義的、富有挑戰性的，這些內容要有利于學生主動地進行觀察、實驗、猜測、驗證、推理與交流等數學活動。因此，教師要努力去創設挑戰性學習任務，在把握好挑戰性任務難度的同時，讓挑戰性任務具有探究性、綜合性、開放性，讓學生在認知沖突、認知遇阻、認知失衡中體驗學習，提升學生的認知能力和學習能力。挑戰性學習任務，可以是一個（或幾個）具有較大思維空間的問題，也可以是一項（或幾項）具有挑戰性的活動，還可以是一道（或一組）綜合性的習題等。這些挑戰性學習任務，往往具有“非常規性、非即時性、非單一性、非安然性”等特點。那么，教師在教學中如何設計驅動性問題、運用挑戰性學習任務進行有效教學呢？筆者以單元整體教學理念引領下的四年級上冊第四單元《探秘多邊形》為例，談自身教學實踐的嘗試與思考。

一、創設探究性任務鏈，提升思維結構

任務鏈，是將一個大挑戰性任務分解成若干個小挑戰性任務，這些小挑戰性任務之間具有內在的邏輯關聯，像鏈條一樣彼此銜接、勾連。在這一探究過程中，學生的思維會不斷進階，結構逐步趨于完善。

四年級上冊第四單元《探秘多邊形》中關于“高”的教學，一直都是難點，教師教得辛苦，學生學得迷糊。教材原來的編排是分散在不同課時進行學習：信息窗1中先認識三角形的底和高；信息窗3 中再認識平行四邊形和梯形的底和高。我認為這樣的結構編排并不利于學生對高的本質把握，依據單元整體教學理念，我創造性地將這三種平面圖形的高融合在一課時進行探究，并設計如下遞進性問題學習任務鏈，引領學生在解決“問題串”的過程中，讓探究逐漸走向深入，接近數學的本質。

《認識底和高》任務鏈

第一鏈：由“樹高”引入到“三角形的高”

①這里有一棵小樹，你認為從哪里到哪里才算是樹的高？

②現在刮臺風樹歪了，跟原來相比，此時的樹變高了還是變矮了？這時的樹高，指的是從哪里到哪里的高度？

③小樹有高度，那三角形有高嗎？（出示三種三角形：銳角三角形、直角三角形、鈍角三角形）請你嘗試在圖中畫出來。

④你覺得給三角形畫高，你可以聯想到以前學過的什么類似的知識？

第二鏈：由“橋高”引入到“梯形、平行四邊形的高”

①一輛貨車正在公路上行駛，前面有一座橋，限高4.5 米。這里的高4.5 米，指的是從哪里到哪里的距離？只有這一條高嗎？你覺得會有多少條這樣的高？為什么？

②橋有高度，那梯形有高嗎？（出示梯形）請你嘗試在圖中畫出來。梯形的高，只有這一條嗎？你覺得會有多少條這樣的高？為什么？梯形的這兩條腰上也有高嗎？為什么？

③平行四邊形有高嗎？（出示平行四邊形）請你嘗試在圖中畫出來。平行四邊形的高，只有這一條嗎？你覺得會有多少條這樣的高？為什么？平行四邊形的這兩條對邊上也有高嗎？為什么？

④你覺得給梯形和平行四邊形畫高，這讓你聯想到以前學過的什么類似的知識？

第三鏈：整合關聯，凸現異同——尋找高的本質

①對比這3 種平面圖形的高，你有什么發現？它們的相同點是什么？不同點是什么？

②我們今天學習的底和高，對今后的學習有什么用呢？

生活經驗是學習的起點，由真實情境“樹高、橋高”引入三角形的高、梯形的高、平行四邊形的高，符合學生的認知規律。通過對比，學生會發現“高”的本質就是之前三年級學習的“點到直線之間的垂直線段”，此時只是把它放在了圖形中而已，這是這三種高的相同點；不同點是三角形的高是指點到直線的垂直線段，而梯形和平行四邊形的高則是指平行線之間的垂直線段。梯形與平行四邊形的高，共性中也有個性的體現：梯形因為只有一組對邊平行，所以只有一種長度的高，而平行四邊形因為有兩組對邊平行，所以可能會有兩種長度的高。這樣，一節課中同時呈現三種平面圖形的高，有利于學生經歷完整的問題探究過程，通過對比，發現異同，歸納本質，提升思維結構層級。

二、創設“三學”化任務單，優化學習結構

學習任務單，是學習支架的主要形態，是教師依據學情，為達成學習目標而設計的學習活動的載體。同一內容，在不同的時間段——學前、學中、學后，根據承載的側重點不同，可以設計一系列的學習任務單，以期優化學生的知識結構。

學前單，即在課堂學習前設計的學習任務單，重在讀懂學生，了解學生已有什么，還需什么，能學什么，明確學生認知起點在哪里，認知目標到哪里，認知路徑是什么，從而真正實現因材施教和學習結構重組。

第四單元《探秘多邊形》中關于《三角形的內角和》一課，教師設計了這樣一份學前任務單：

《三角形的內角和》學前單

同學們，我們已經知道三角形根據角來分，可以分為銳角三角形、直角三角形、鈍角三角形。

[提出猜想]三角形的內角和可能是______度？

[操作驗證]我們用不同類型的三角形來研究一下吧。

你想用什么方法來驗證你的猜想？將你的驗證過程用你喜歡的方式呈現出來。

[得出結論]__________________。

[反思評價]除了上述這種方法，你還想到了什么方法也可以驗證?

通過你的操作驗證，你還有什么發現？還有什么困惑？

學中單，即課堂學習中設計的學習任務單，重在學法指導，調控關聯活動，培養高階思維。通過設計挑戰性學習任務，以核心知識學習為原點，學生通過探究自主發現相關、相近的知識元素的關系，形成“連點成線、由線成面”整體融通的知識體系。

在《三角形的內角和》一課中，教師設計了這樣一份學中任務單：

《三角形的內角和》學中單

同學們，現在我們已經知道了三角形的內角和是180°。那么，四邊形的內角和是多少度？它與三角形的內角和有沒有關系？小組合作，共同探究。

[提出猜想]四邊形的內角和可能______度？

[操作驗證]我們用不同類型的四邊形來研究一下吧。

你們想用什么方法來驗證你們的猜想？將你們的驗證過程用喜歡的方式呈現出來。

[得出結論]___________________。

[反思評價]四邊形的內角和與三角形的內角和有什么關系？為什么會有這種關系？

（長方形、正方形、平行四邊形、梯形……）

學后單，即課堂學習后設計的學習任務單，重在遷移運用，一是體現內容遷移，學習的最終目的是運用，在運用中加深理解，促進思考，使思維向廣度與深度兩個方向發展；二是體現分層選擇，根據學生的個性差異，對課后學習任務進行分層設計，學生可以根據自己的興趣和能力選擇不同的挑戰性任務。

在《三角形的內角和》一課中，教師設計了這樣一份學后任務單：

《三角形的內角和》學后單

1.回顧：通過今天的學習，你都學會了用哪些方法來驗證“三角形的內角和是180°”？請你寫一寫或畫一畫。

2.練習：

①李明今天過生日，爸爸送給他一個等腰三角形的風箏，它的一個底角是70°，它的頂角是多少度？

②畫一畫，算一算，你發現了什么？

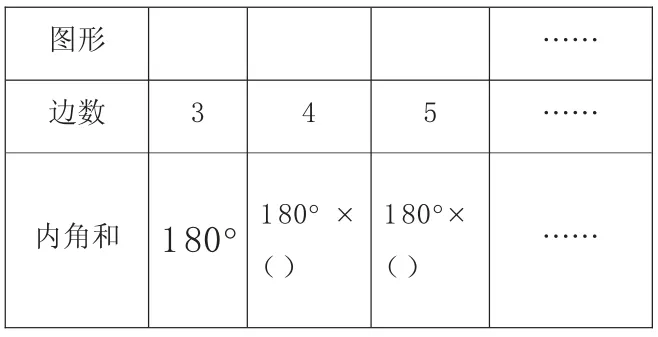
我的發現：___________________。

3.拓展：（二選一）

①課外閱讀《帕斯卡與“三角形內角和”的故事》。

你看明白了嗎? 怎么證明鈍角三角形的內角和也是180 呢?趕緊找個三角形試一試吧!

②繪本賞欣《失落的一角》。

通過賞析，你有什么感想？

“三學”任務單與學習活動的一體化應用，充分體現了“學為中心”的教育理念，不同的生活情境、數學情境的創設，促使了學生學習的高投入，高認知，促使“真學習”的發生。

三、創設開放性任務群，完善認知結構

學習任務群，指以任務為導向，以學習項目為載體，整合學習情境、學習內容、學習方法和學習資源，通過一定的實踐活動將這些因素建立起聯系，從而建構知識和學習體驗，完成相應的任務，提升素養。

第四單元《探秘多邊形》中，按教材的編排全部結束所有的內容之后，為了拓寬學生的視野，提升思維的靈動性，我增設了一節拓展課——《百變多邊形》。通過創設開放性任務群，讓學生在實踐活動中玩轉各種圖形，感受圖形的變幻，探尋圖形之間的關聯，進而完善認知結構。

活動一：巧板36 變

學具準備：每小組提供一套“七巧板”。

任務1：從七巧板中選取其中的三塊板拼成一個平行四邊形。

任務2：從七巧板中選取其中的三塊板拼成一個三角形。

任務3：從七巧板中選取其中的三塊板拼成一個梯形。

任務4：先利用七巧板的七塊板拼成一個大三角形（如上圖所示），再只能動一步，將這個大三角形變成平行四邊形。

活動二：圖形魔術

學具準備：每小組提供2 張相同的平行四邊形紙片、2 張相同的三角形紙片（銳角三角形、直角三角形、鈍角三角形中的一種）、2 張相同的梯形紙片。

任務1：將一張平行四邊形紙剪成兩部分，再拼成一個長方形。①說一說你是怎樣剪拼的？有幾種拼法？②拼成的長方形與原來的平行四邊形有什么關系？

任務2：選擇一個或兩個完全一樣的三角形，通過怎樣的操作可以將其轉化為我們學過的圖形？轉化后的圖形與原來的圖形相比，有什么關系？

任務3：選擇一個或兩個完全一樣的梯形，通過怎樣的操作可以將其轉化為我們學過的圖形？轉化后的圖形與原來的圖形相比，有什么關系？

開放性的學習任務群，通過知識的條件化、情境化、結構化，給學生的思維發展創設了更為寬廣的空間，讓不同思維水平的學生都能獲得探索的機會和成功的愉悅，既豐富了學生的學習活動經驗，又實現了學生對知識的深度理解，進一步完善了認知結構。

數學雖注重理性思維培養，但數學學習也是有溫度的。在任務驅動式小學數學教學中，教師應為學生搭建一個以知識結構為載體，情意結構為動力，思維結構為核心，認知結構為發展的立體式結構，設計帶有挑戰性的學習任務，激發學生主動探究的欲望，通過自助、互助，引發學生自身深度思考，使其知識結構合理轉化、情意結構逐步細化、思維結構持續深化、認知結構完善優化，驅動結構化思維，促使深度學習的發生。