基于改進鴿群算法的無線傳感器網絡定位方法*
崔煥慶,張 娜,羅漢江
(山東科技大學計算機科學與工程學院,山東 青島 266590)
無線傳感器網絡(Wireless Sensor Networks,WSNs)由大量傳感器節點組成,廣泛應用于環境監測、智慧城市、災害救援和目標追蹤等領域。 確定傳感器節點的位置信息為許多位置感知協議和應用程序提供了基礎支持,因此,節點定位是無線傳感器網絡的關鍵技術之一[1]。 由于成本因素,為每個節點配備全球導航衛星系統(Global Navigation Satellite System,GNSS)進行定位是不現實的。 目前常用的方法是先給部分節點配備GNSS 以獲取其自身位置并輔助其他節點進行定位,將已知自身位置的節點稱為錨節點,其他節點稱為未知節點[2]。
目前定位算法可分為無需測距和基于測距兩類[3]。 前者根據節點間的連通信息估計距離,后者需要測量節點之間的距離或角度。 相比于無需測距的定位算法,基于測距的定位算法精度更高[4]。 獲得距離后,使用三邊測量、極大似然估計(Maximum Likelihood Estimation,MLE)等估計節點位置[5]。 相比于傳統的定位算法,智能優化算法計算精確、計算復雜度低,被廣泛應用于節點定位中。 ISSADVHop[6]算法通過修正DV-Hop 的平均跳距,并使用佳點集和Levy 飛行策略對麻雀搜索算法進行改進,改善了定位精度。 AWL-MC[7]算法采用非線性映射曲線距離分析對未知節點進行粗略的相對坐標定位,再通過線性變換將相對坐標轉換成絕對坐標,最后采用自適應Levy 飛行優化鯨魚算法,以提高定位精度。 OLSSO[8]算法先通過Bounding-box 方法得到未知節點可能存在的區域以初始化個體,后將加權中心反向學習策略與群居蜘蛛群優化算法相結合,具有較高的定位精度和較快的收斂速度。
目前,鴿群算法(Pigeon Inspired Optimization,PIO)[9]已廣泛應用于各個領域,PIO 相比于粒子群優化(Particle Swarm Optimization,PSO)[10]、蝙蝠算法(Bat Algorithm,BA)[11]等,具有收斂速度快、參數較少和穩健性強等優點,但是容易陷入局部最優[12]。 為此,本文提出了一種基于改進鴿群優化(Modified Pigeon Inspired Optimization,MPIO)的定位算法。 本文的主要貢獻有:①為了解決PIO 容易陷入局部最優的問題,設計了一種改進鴿群算法即MPIO 算法,在保持快速收斂能力的同時,提高了PIO 的計算精度。 ②將MPIO 算法應用于無線傳感器網絡節點定位以提高性能。
本文組織如下。 第一部分介紹了網絡模型,第二部分介紹了標準鴿群算法,第三部分介紹了MPIO 算法及其在定位中的應用,第四部分給出了仿真實驗和結果分析,最后第五部分總結了全文。
1 網絡模型
假設WSN 由N個傳感器節點組成,節點在部署完后不再移動。 錨節點數為M,第i個錨節點的坐標記為Ai=(xai,yai)。 第j個未知節點的實際坐標記為Uj=(xuj,yuj),估計坐標記為^Uj=(^xuj,^yuj)。傳感器節點通信范圍是一個半徑為R的圓,錨節點向其通信范圍內的節點廣播信息,所廣播的用于輔助未知節點定位的信息稱為信標信息,包含錨節點坐標和發送信號強度兩個字段。 傳感器節點使用接收信號強度(Received Signal Strength,RSS)測距,RSS 采用對數-常態分布無線信號傳播模型[13],即:

式中:d0為參考距離,PL(d0)為傳播距離為d0時的接收信號功率。d為參考節點與未知節點間的距離,Prx為傳播距離為d時的信號接收功率。η為路徑損耗因子,Xσ為均值為0,標準差為σ的高斯變量。
在實際應用中,由于多徑衰弱、信號傳播不穩定和噪聲等因素,傳感器節點的通信范圍不是一個規則的圓,所以使用通信不規則度(Degree of Irregularity,DOI)進行建模[14]。 DOI 值越高,通信范圍受環境影響越嚴重。 DOI 定義如下:

式中:Kθ表示第θ個方向上的不規則度,滿足|K0-K359|≤DOI,r∈[0,1]是一個服從均勻分布的隨機數。 使用DOI 后的信號傳播模型定義為:

設錨節點Ai和未知節點Uj的實際距離為dij,使用RSS 測得的距離為^dij。 通過最小化dij與^dij之差來達到估計未知節點位置的目的,所以使用智能優化算法定位的適應度函數定義如下:

式中:n為Uj通信范圍內的錨節點數,X為智能優化算法中的個體位置。
平均定位誤差(Average Localization Error,ALE)定義為全部未知節點估計坐標與實際坐標之間歐氏距離的均值,即:

2 標準鴿群算法
PIO 是模仿鴿子歸巢行為的一種智能優化算法。 鴿子歸巢可分為兩個階段,在不同階段使用不同的導航工具。 在地圖和指南針算子階段,鴿子通過感知磁場生成地圖,把太陽作為指南針調整飛行方向。 在飛向目的地的過程中,其對磁場和太陽的依賴性減少。 在D維搜索空間中,第i只鴿子的位置Xi和速度Vi按照下式進行更新:
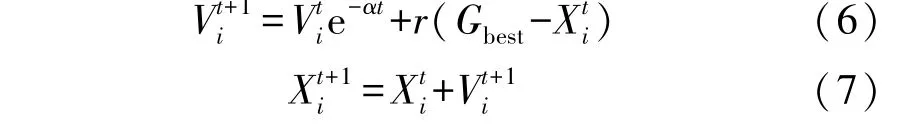
式中:t為當前迭代次數,α∈(0,1)為地圖和指南針因子,Gbest為全局最優位置。 記T1max為該階段最大迭代次數,當t>T1max時,進入下一階段。
在地標算子階段,每次迭代時先根據適應度值將鴿子排成非減序,保留前一半鴿子;然后在剩余鴿子中計算加權中心位置作為鴿子飛行的參考方向。鴿子位置更新如下:

式中:Np為鴿子總數,Xc為加權中心位置,f(·)為適應度函數。 記T2max為該階段最大迭代次數,當t>T2max時,地標算子停止工作。
3 改進鴿群算法
3.1 地圖和指南針算子階段
在該階段,PIO 算法的全局搜索能力主要由指數權值W=e-αt決定,使得鴿群在迭代過程中多樣性呈遞減趨勢并逐步向最優解收斂[15]。 這種更新方式使算法快速收斂,但是全局搜索能力較差。 地圖和指南針因子α在很大程度上決定了算法全局搜索能力的優劣。 圖1 展示了指數權值W在T1max=50 時的變化情況。α=0.3,t<15 時,W<0.75,種群多樣性快速減少;而t≥15 時,W≈0,種群多樣性喪失,算法主要在Gbest附近進行局部搜索,失去了全局搜索能力,導致過早收斂。α=0.02,t=50 時,W=0.38,算法不易收斂。 0.02<α<0.3 時,W呈指數遞減趨勢,種群多樣性快速減少,導致較差的全局搜索能力。

圖1 指數權值隨迭代次數變化圖
為平衡全局搜索與局部搜索,改進式(6)為:

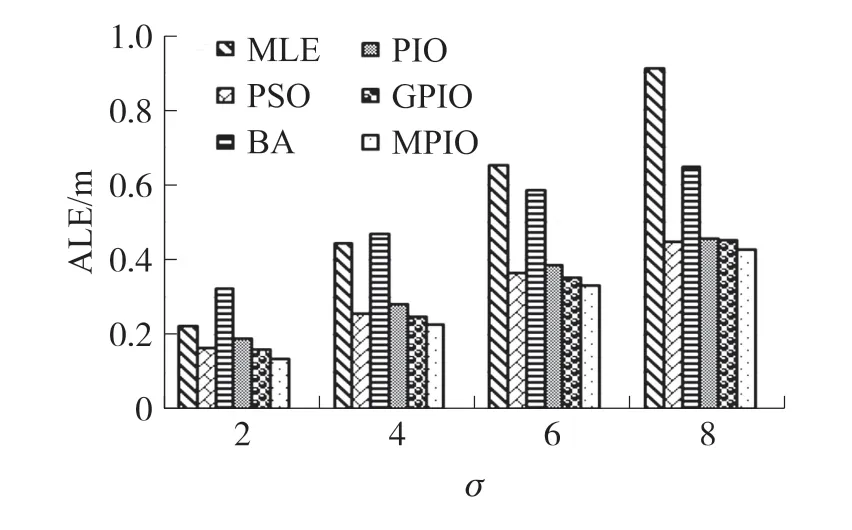
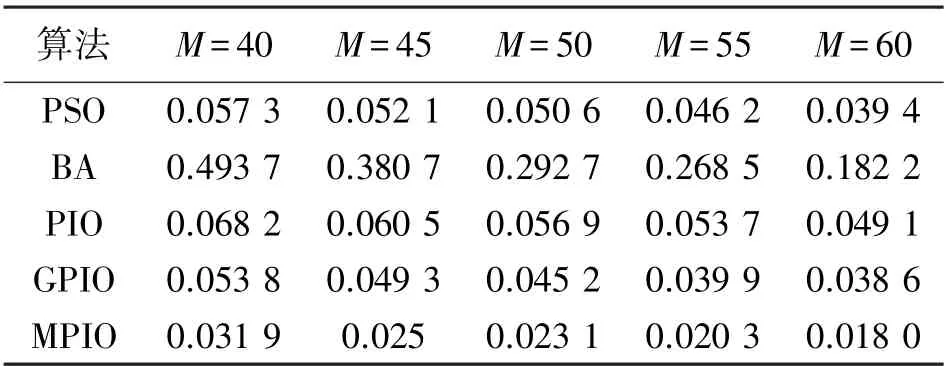
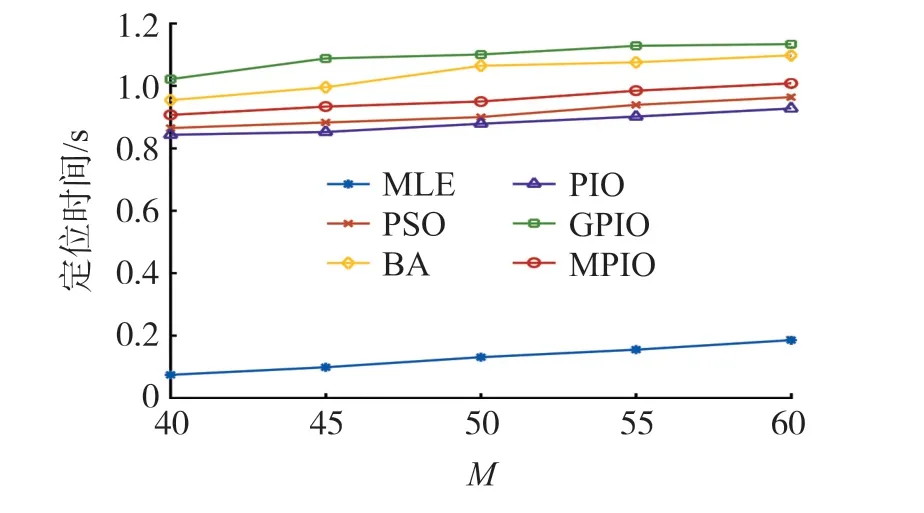
α=0.3 時,改進后的指數權值W′=1-e-αt的變化情況如圖1 所示。t≤4 時,W′<0.6,僅在Gbest附近搜索,能夠更快地在Gbest處收斂;4 在該階段,MPIO 不刪除鴿子,而是按照適應度值排序后將鴿子分為兩組種群,在不同種群中用不同方式進行迭代更新。 定義: 前N′p只鴿子為一組,鴿子位置更新公式為: 式中:Xpi為第i只鴿子的局部最優位置。 剩余Np-只鴿子分一組,使用隨機游走和捕食機制更新鴿子位置。 隨機游走是在最優解附近產生局部新解,在一定程度上能夠使算法跳出局部最優,即: 式中:β∈[-1,1]是一個隨機變量,E∈(0,1)為一個常數,為第i只鴿子在第t次迭代時的脈沖發射率。 捕食機制中,鴿子會減少響度Li,增大ri,擇優選擇鴿子位置并更新Li和ri,即: 式中:ε∈[0,1]為常數,表示響度衰減系數;μ>0 為常數,表示脈沖增強系數;=0.7 表示第i只鴿子的初始脈沖發射率,設置每只鴿子的響度Li初始值為0.1。 使用MPIO 進行定位的基本思路是:錨節點廣播信標信息后,未知節點使用RSS 測量與鄰居錨節點的距離。 在測得至少3 個相鄰錨節點的距離、位置后,便采用MPIO 算法進行位置計算。 具體流程如算法1 所示。 輸入:未知節點U 及其相鄰錨節點集合A輸出:^U=(^xu,^yu)1. 初始化D,Np,T1max,T2max,α,E,ε,μ 2. 使用RSS 估算U 到每個錨節點的距離3. 隨機生成Np 只鴿子,第i 只鴿子坐標為Xi(i =1,2,…,Np)4. 使用式(4)計算適應度函數值5. Gbest←最佳位置6. for t←1 to T1max do 7. 所有鴿子根據式(11)和(7)更新位置8. 使用式(4)計算適應度函數值9. 更新Xp 和Gbest 10. t←t+1 11. end for 12. for t←1 to T2max do 13. 根據適應度函數值對鴿子進行排序14. 根據式(12)和(13)更新N′p和Xc 15. 前N′p只鴿子根據式(14)更新位置16. 其余鴿子根據式(15)更新位置17. 使用式(4)計算適應度函數值18. 更新Xp 和Gbest 19. t←t+1 20. end for 21. return Gbest 算法1 第1 行初始化必要參數,第2 行使用RSS 測量未知節點與錨節點的距離,第3~5 行初始化鴿群,第6~11 行是地圖和指南針算子階段,第12~20 行是地標算子階段,每階段使用不同的公式更新鴿子位置。 第21 行返回Gbest作為未知節點U的估計位置。 該算法的主體是兩個for 循環,每個for 循環都是根據上述公式對鴿子位置進行更新,其中第2 個循環需要對鴿子進行排序,因此其時間復雜度為O(NpT1max+NpT2maxlogNp)。 本文使用MATLAB R2016b 進行仿真,所有算法運行50 次并取均值作為實驗結果。 在定位精度上將MPIO 與MLE、PSO、PIO、BA、GPIO[16]算法相比較。 各算法參數設置如表1 所示,其他實驗參數設置如表2 所示。 表1 優化算法的參數設置 表2 其他實驗參數設置 在錨節點數M=50,通信半徑R=20,25,30,35,40 時的結果如圖2 所示。 隨著R的增加,平均定位誤差ALE 隨之下降,原因在于R的增大使得孤立節點的數量大幅減少,距離測量更加準確。 BA 算法的ALE 最大,因為其在較大的部署區域內尋優能力較差;其次是MLE,它計算簡單,但是求解能力較差;其次是PIO 和PSO 算法,因為PSO 和PIO 都有容易陷入局部最優的局限性;GPIO 通過在距離較近的種群個體上添加高斯變異使種群個體隨機發散,并沒有有效解決算法陷入局部最優。 MPIO 算法的定位精度始終優于其他算法,GPIO、MPIO 相比于PIO 分別提高了30%、60%。 MPIO 算法具有更優的求解能力,一方面是因為添加了自適應調整機制,使種群個體快速尋找全局最優并提高了種群在最優解附近的局部搜索能力;另一方面是因為種群分組和隨機游走機制增加了種群多樣性,使算法能夠跳出局部最優。 圖2 通信半徑對定位誤差的影響 在通信半徑R=30,錨節點數M=40,45,50,55,60 時的結果如圖3 所示。 隨著錨節點數量的增加,未知節點接收到的信標信息更多,平均定位誤差ALE 會隨之下降。 BA 算法的ALE 最大,因為其在較大的部署區域內尋優能力較差;其次是MLE,它計算簡單但是求解能力較差;其次是PIO 和PSO,因為PSO 和PIO 都容易陷入局部最優;GPIO 沒有有效改進PIO 容易陷入局部最優的缺陷。 MPIO 算法的定位精度始終優于其他算法,GPIO、MPIO 相比于PIO 分別提高了33%、60%。 MPIO 算法的自適應調整機制和隨機游走機制增加了種群多樣性,有效提高了PIO 算法的求解精度。 在相同條件下,MPIO算法所需的錨節點數量最少,能有效減少網絡成本。 圖3 錨節點數量對定位誤差的影響 在錨節點數M=50,通信半徑R=30,測距誤差σ=2,4,6,8 時的結果如圖4 所示。 隨著σ的增加,平均定位誤差ALE 也隨之增大。 MLE 受測距誤差影響最大;其次是BA 算法,因為其在較大的部署區域內尋優能力較差;其次是PIO 和PSO,因為PSO和PIO 都容易陷入局部最優;GPIO 沒有有效改進PIO 容易陷入局部最優的缺陷。 MPIO 算法的定位精度始終優于其他算法,GPIO、MPIO 相比于PIO 分別提高了27%、49%。 MPIO 算法的自適應調整機制和隨機游走機制使算法跳出局部最優,有效提高了PIO 算法的求解精度。 相同條件下,MPIO 算法受測距誤差的影響最小。 圖4 測距誤差對定位誤差的影響 在錨節點數M=50,通信半徑R=30,通信不規則度DOI=0.05,0.1,0.15,0.2,0.25 時的結果如圖5所示。 DOI 越大,節點通信范圍越不規則,平均定位誤差ALE 也隨之增大。 BA 算法受DOI 影響使得ALE 最大,因為其在較大的部署區域內求解能力較差;其次是MLE,它計算簡單但是求解能力較差;其次是PIO 和PSO,因為PSO 和PIO 都容易陷入局部最優;GPIO 沒有有效改進PIO 容易陷入局部最優的缺陷。 MPIO 算法的定位精度始終優于其他算法,各算法受DOI 影響定位誤差的波動幅度分別為:MLE 0.79%、PSO 1.12%、BA 4.63%、PIO 1.32%、GPIO 1.34%、MPIO 0.91%。 MPIO 算法的自適應調整機制和隨機游走機制有效改進了PIO 算法容易陷入局部最優的缺陷。 相同條件下,MPIO 算法受DOI 的影響變化幅度較小。 圖5 DOI 對定位誤差的影響 在錨節點數M=50,通信半徑R=30 時的收斂曲線如圖6 所示。 在算法迭代前期MPIO 算法的收斂最快,其次是GPIO、PIO、PSO 和BA。 圖6 不同算法收斂曲線 圖7 和表3 分別顯示了在錨節點數M=40,45,50,55,60 時不同定位算法的定位時間和最優適應度值。 可以看出隨著錨節點數量的增加,定位時間也隨之增加,各定位算法平均定位時間依次為MLE 0.129 s、PIO 0.881 s、PSO 0.92 s、MPIO 0.95 s、BA 1.04 s、GPIO 1.09 s。 隨著錨節點數量的增加各優化算法的適應度值減小,各優化算法的平均適應度值依次為MPIO 0.023、GPIO 0.045、PSO 0.049、PIO 0.057、BA 0.323。 由于MLE 算法計算簡單所以定位時間最短,但是由4.1 節分析可知MLE 算法定位精度較低;BA 具有較長的定位時間和較高的最優適應度值;由于PIO 收斂速度較快所以定位時間較短,但是由于容易陷入局部最優導致PIO 的最優適應度值高于MPIO;由于GPIO 頻繁使用高斯變異增加種群多樣性提高算法求解精度,使最優適應度值較低,但是定位時間最長;由于MPIO 在PIO 的基礎上進行改進來使PIO 跳出局部最優,所以定位時間較PIO 長,但是具有最低的適應度值,算法求解精度最高。 表3 各優化算法的最優適應度值 圖7 錨節點數量對定位時間的影響 本文針對PIO 算法容易陷入局部最優的缺陷,提出了一種基于改進鴿群算法(MPIO)的無線傳感網絡定位算法。 MPIO 的第一階段通過自適應調整機制來平衡全局搜索與局部搜索能力,并同時保證較快收斂速度;第二階段保留全部鴿子并分組,使用隨機游走等機制增加種群多樣性,提高了算法的求解精度。 定位過程中首先使用RSS 進行測距,然后使用MPIO 進行定位。 仿真結果表明,MPIO 算法相比于傳統的定位算法和其他的優化算法,具有較高的定位精度和較快的收斂速度。3.2 地標算子階段
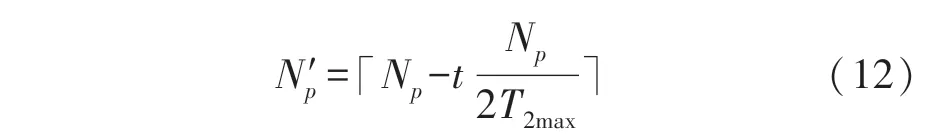



3.3 基于MPIO 的定位算法


4 仿真實驗


4.1 定位精度對比



4.2 收斂速度對比

5 總結

