一種基于輪廓邊緣的直線擬合算法*

譚仁虎，胡小平，彭向前*，陳立鋒，黃 泓

(1.湖南科技大學機電工程學院，湖南 湘潭 411100；2.湖南科技大學機械設備健康維護湖南省重點實驗室，湖南 湘潭 411100)

直線是日常生活中常見的一種幾何結構，通常會出現在物體的邊緣[1]，直線段包含了場景中最基本的幾何信息和拓撲信息，可以作為檢測圖像高層特征或分析圖像內容的基礎[2]。 直線特征作為一種規則離散點集，相對于點特征能夠提供更加明確、豐富的結構信息，直線特征提取是圖像分析領域的一個經典問題，被廣泛應用于自動駕駛、工業檢測[3]、圖像匹配和相機標定等諸多領域。 因此，研究出快速而準確的直線特征提取算法是非常有意義的。

在直線檢測方面的研究中，國內外學者已經取得了不少研究成果。 董晶等人[4]提出了一種結合主元方向和梯度方向的快速直線段檢測算法，根據主元一致性和直線誤差度篩選出有效檢測直線段，并利用最小二乘擬合得到正確的直線段。 但是該算法依賴于用canny 算子提取邊緣特征，算法的調整參數較多，自適應調整不佳。 亢潔[5]提出一種抗干擾性強的作物行檢測算法，通過輪廓查找，求取輪廓的外接矩形，然后在所求矩形內進行線掃描，記錄直線上的綠色像素數量最大時為最佳作物行直線，該算法的應用比較局限，對其他領域的適用性不足。

Grompone von Gioi 等人[6]提出了一種快速檢測直線段方法，稱為LSD 算法。 通過降采樣的方式提高圖像的質量，結合像素的梯度信息生成直線擬合區域，之后將區域看成矩形候選直線段，依據Helmholtz 原則[7]對直線段進行驗證。 該算法檢測的是圖像矩陣中所有的直線，但是在很多視覺任務中往往只需要最具代表性的直線特征，并且將截斷的線段重組起來，檢測出更接近人類感知的線段。

Naila Hamid[8]提出了一種算法合并破碎的線段，該算法根據線段的角度接近度和空間接近度進行分組，將每組內符合算法要求線段合并為單個線段，重復此步驟，直到沒有更多的線段可以合并。 該算法雖然能檢測出更接近人類感知的線段，但是它求得的是多條直線特征，并不能找出最具代表性的直線特征，而且實際檢測中的目標直線往往會受到種類各異和不定大小的噪聲干擾，該算法容易受到背景信息與噪聲的干擾，達不到高精度檢測任務的要求。

鑒于上述算法的不足，本文提出了一種基于輪廓邊緣的直線擬合算法，實驗證明該算法具有良好的抗干擾性和適用性。

1 邊緣檢測

本文研究的核心是基于圖像輪廓邊緣提取直線特征，于是準確獲取目標直線的輪廓邊緣尤為重要。以圖1(a)為例，用二值化邊界掃描、canny 算子邊緣檢測、Laplace 算子邊緣檢測、Sobel 斜向算子邊緣檢測四種邊緣提取算法和本文邊緣提取算法的效果作對比。

如圖1(b)所示，二值化掃描邊界的方法，抗干擾性極差，會導致目標像素的大量損失；如圖1(c)所示，Canny 算子是一種不錯的邊緣檢測方法，但是高、低閾值的設置，不能根據圖像自身的特點來確定，需要根據經驗，人為預先設定，而且容易使噪聲形成虛假的邊緣[9]，給算法的計算帶來難度。 如圖1(d)所示，Laplace[10]算子是一種各向同性的算子，對孤立像素的響應比對邊緣或線的響應更敏感，所以它只適用于無噪聲的圖像，會產生雙邊效果，不容易得到單像素的邊緣特征，也不能得到離散的輪廓線，無法準確的進行分類計算。 Sobel 算子具備一階算子算法簡單，處理速度快的優點，由于使用了加權平均算法，因此對圖像中的一些噪聲具有一定的抑制能力[11]。 如圖1(e)所示，Sobel 斜向算子可以快速而準確地獲得目標直線的單像素點集，還能初步篩選掉一些干擾噪聲[12]；但是檢測目標的位置會對檢測效果產生影響，而且對水平線段不敏感，提取的邊緣特征連續性不好。

綜合檢測有效像素點的個數和實際邊緣檢測的準確度，以及減少后續算法的難度，本文選用了改良的Sobel 斜向算子和Sobel 水平算子3×3 的掩膜矩陣結合篩選條件作為邊緣提取算法。 針對檢測目標的位置，選擇相應的方向梯度矩陣，梯度突變的地方就是輪廓邊緣的位置，將突變的連續像素點作為一個輪廓點集記錄下來，得到輪廓邊緣的集合。

圖2(a)為圖像任意一個3×3 子區域像素點的位置示意圖，P為對應像素點的灰度值。 式(1)為掩膜計算公式、通過式(2)計算得出Sobel 斜向算子和Sobel 水平算子3×3 掩膜矩陣卷積到的梯度值。本算法是在二值化的圖像中提取邊緣特征，通過歸一化把灰度值低于二值化閾值的置為0，高于二值化閾值的置為1；圖2(b)中的W為3×3 的Sobel 斜向算子卷積核權重的大小。

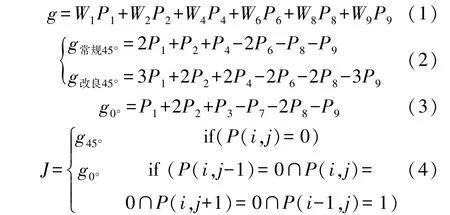
圖2 卷積核

本文提出的改良Sobel 斜向算子，降低了中心四鄰域像素權重(W2、W4、W6、W8)與對角鄰近像素權重[13](W1、W3、W7、W9)；以45 度梯度方向作為實例詳解，常規的斜向G常規45°與改良的斜向G改良45°(其余梯度方向對應適用)，圖3(a)示例1 表示一個孤立的像素點，圖3(b)示例2 表示連續的兩個像素點，用式(1)和常規的斜向g常規45°計算兩個示例的梯度值都為2，無法區分像素邊界情況，通過本文改良的斜向g改良45°能計算出圖3(a)梯度值為3，圖3(b)梯度值為4，據此可以設定梯度閾值為3 來排除圖3(a)的假邊界像素，檢測出更貼近真實邊緣的像素點集。 式(4)中的P(i，j)為像素點的位置，J為對應條件下求出的梯度值，當J大于3 時即可將像素點P(i，j)判斷為邊緣像素點，納入初步預測點集。

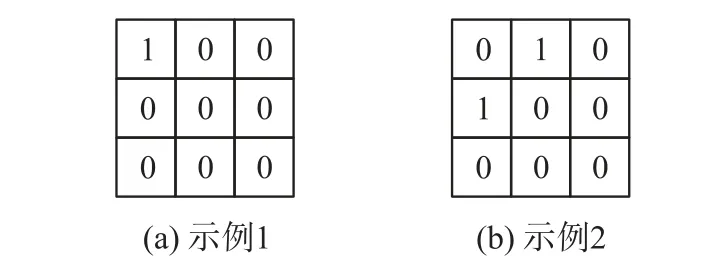
圖3 示例邊緣

本文邊緣提取算法是為了獲得最具代表性的直線特征，如圖4 所示，設置了①截斷線段、②粗線段、③分割線段、④曲線、⑤鋸齒線段五種情況來驗證本文改良的Sobel 邊緣檢測算法較常規Sobel 算法的優越性，圖5 為邊緣檢測算法效果圖，算法結果分析見表1。

雖然我國政府目前對林業的重視程度較高，但在投資上仍存在一些不足，基礎設施不完善，林業道路建設尚未實施，部分受損道路未能及時修復。此外，基層工作環境惡劣，人才外流，部分林業種植基地因投入資金不足而未能種植優質苗木。相關科研宣傳工作尚未落實。

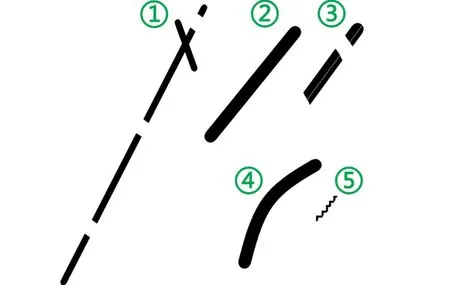
圖4 測試圖2

圖5 邊緣檢測算法效果圖

表1 算法結果分析

2 邊緣分類

2.1 優化的最小二乘法擬合直線

最小二乘法通過使誤差的平方和最小化，尋找數據的最佳函數匹配，利用最小二乘法，可以方便地求出未知的數據，并將所得數據與實際數據之差的平方累積和最小。 傳統的最小二乘法擬合直線的原理是用“殘差平方和最小”求出直線的函數模型，但是，很容易受到離散噪點的干擾。

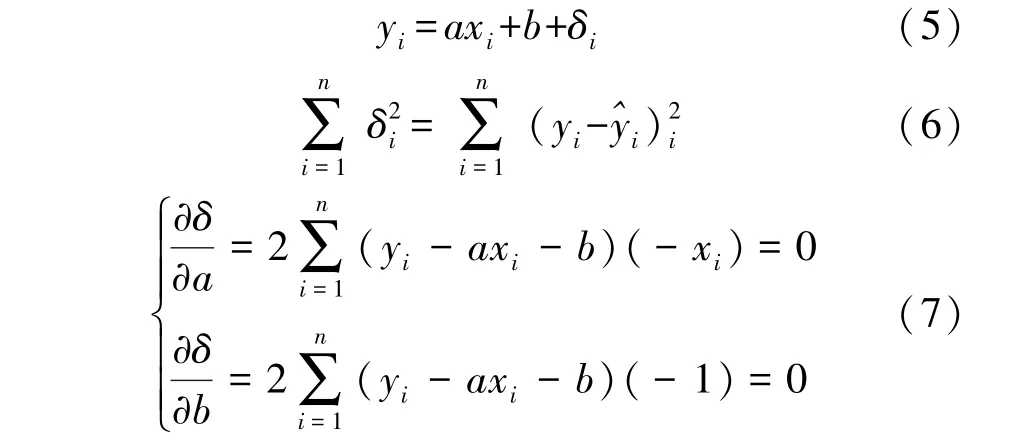
式中:縱坐標yi為對應橫坐標xi的實際值，a為斜率，b為截距，δi為殘差值。 如式(6)求殘差值的平方，殘差值等于實際的縱坐標值yi減去擬合得出的縱坐標。可以把殘差值平方看作以a、b為變量的函數求偏導，得到極值點時的a、b值即為所求，如式(7)。

用最小二乘法[14]除了計算比較方便外，此方法能給出在統計意義上最好的參數擬合結果，但是這種方法對噪聲非常敏感。 所以本文對最小二乘法進行了優化，首先把目標點集進行初步的最小二乘法擬合，通過式(8)計算出點集中每一個點到擬合直線的距離。

根據擬合精度的要求設置距離閾值(與精度成正相關)，判斷Dis 是否小于設定的距離閾值，將符合篩選條件的點放入到擬合點集中進行第二次直線擬合，然后將設定的閾值減1，繼續用目標點集里的點對新擬合出來的直線進行點到直線的距離篩選，如圖6 所示(方形為有效像素點，圓形為無效像素點)。 直到擬合點集中的點到擬合直線的距離都在一個像素點之內后輸出直線擬合結果，流程圖如圖7 所示。

圖6 優化最小二乘法算法示意圖

圖7 優化最小二乘法算法流程圖

2.2 角度空間分類

對每個輪廓用優化的最小二乘法擬合出相應的直線，用擬合優度R2來驗證直線擬合的準確性和可靠性。 擬合優度評價是用于檢驗總體中的一類數據的分布是否與某種理論分布相一致的統計方法。

用式(9)來計算擬合優度，R2最大值為1，如果R2的值越接近1，說明直線擬合算法的擬合程度越好；反之，R2的值越小，說明直線擬合算法的擬合程度越差。

求解出符合擬合優度大于0.9 的直線斜率，因為直線的斜率k的范圍為(-∞，+∞)，而且不是線性變化，無法將其分類，所以將斜率k轉換成角度，取值范圍為(-90，90)，為了便于計算與編程，讓轉換的角度都加上90°[15]，于是取值范圍就變成了(0，180)，繼而以每個區間的大小為1 度把其分成180 個區間，通過計算取模將各個輪廓擬合出來的角度大小進行分類，并把每個區間輪廓的長度累加，篩選長度最長的角度區間作為目標區間。

圖8 插值計算示意圖

然后通過相應的角度值找到對應的輪廓序號將所有求出的輪廓放到一個容器中并以黑底白線畫到另一張臨時圖像中，得到點集篩選后的效果圖，如圖9所示。

圖9 點集篩選效果圖

3 邊緣重組

確定一條直線需要知道斜率和截距，斜率的取值可以轉換為角度進行量化分類，但截距不好進行量化，在直角坐標系中截距受斜率的影響，它不是線性變化的，所以本文算法提出了一種旋轉掃描的辦法來獲取目標點集。

首先，計算出目標區間所有直線擬合的角度平均值；然后減去前面分區間時附加的90°作為圖像矩陣旋轉[16]的角度，讓目標區間里的輪廓線處于水平狀態，式(10)為旋轉矩陣，式(11)為逆旋轉矩陣[17]。 考慮到目標輪廓線如果是一條跨越整個目標圖像的對角線，進行旋轉后，輪廓線端部的像素點會超出圖像邊界造成像素點的損失，影響準確度，所以需要擴大目標圖像的邊界。 式(12)中的H和W分別為源圖像的高和寬，計算出對角線L的長度，然后用式(13)向上取整得到需要擴展后的圖像寬度＾W。 本算法的目的是把目標線段旋轉為水平狀態，為減少后續算法的計算量，只需擴展圖像的寬。如圖10，原圖大小為696×564 pixel，經過擴展的大小為896×564 pixel。

圖10 圖像旋轉效果圖

經過圖像旋轉后，目標線段會旋轉到與x軸角度很小的位置，在創建掃描矩陣時，為了防止目標像素的損失，將掃描矩陣的寬度與圖像的寬度設為一致，高度的設定按邊緣分類時的區間寬度根據式(14)算出，式中h為掃描區間高度大小。

如圖11 所示，像素原點為遍歷的起始位置，按箭頭遍歷全圖后，得到目標區間。

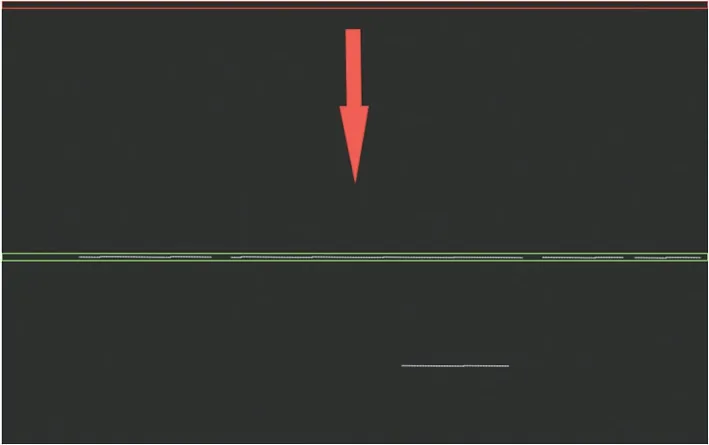
圖11 掃描矩陣示意圖

圖12 為測試圖的局部灰度分布圖，通過掃描矩陣以像素坐標y軸從小到大進行遍歷，統計出所有非0 的像素點，得到像素個數最多的掃描區間。 然后通過式(11)對圖像進行逆旋轉得到點集圖13，再用式(14)在圖14 上截取一個起始點為(X，Y)，高和寬與源圖像一致的矩形框，截取ROI得到圖15，最后，再遍歷復原圖像中的非0 像素得到最終的目標點集，進行優化的最小二乘法擬合。

圖12 局部灰度圖

圖13 篩選效果圖

圖14 逆旋轉處理圖

圖15 復原點集圖

4 驗結果及分析

本文算法在處理器Intel(R)Core(TM)i5-8300H CPU＠2.30GHz，內存8GB，操作系統為Windows 10 64 位的電腦上使用 C + + 在 Visual Studio2017 仿真實現。

為了驗證本文算法的有效性和優越性，對測試圖片分別使用了霍夫直線檢測和最小二乘法做比較，效果圖如圖16。

圖16 擬合效果對比圖

圖16(a)的霍夫直線檢測需要人為地根據圖像調整參數閾值，工程適用性極差，算法檢測出來的直線都是一些離散的線段，就算是在同一條線段上也會檢測出多條離散的線段，每一條線段都有它的直線特征，所以導致目標不明確；而且離散的線段沒有整合起來的線段的像素個數多，導致擬合的準確性較低。 圖16(b)是用最小二乘法擬合出來的效果圖，該算法極易受到噪聲的干擾，算法穩定性差，無法找到準確的直線特征。 圖16(c)是本文提出算法的效果圖，克服了上述兩種檢測算法的弊端，能夠準確地找出目標線段的直線特征。

本文算法在工程實踐中也得到了較好應用，如表2 展示了對某注塑件的幾種惡劣情況的圖像處理效果，通過對1 000 個產品進行測試，用霍夫直線檢測和最小二乘法檢測都無法得到正確的產品邊緣，而本文算法能精準地抓取目標邊緣，準確地提取直線特征，產品定位合格率達98.5%，實驗應用表明，采用該算法進行特征定位能滿足實際應用的要求。

表2 實驗結果對比

5 結束語

本文算法主要是通過改良的邊緣檢測算子得到單像素的輪廓邊緣，按設定的擬合優度閾值初步篩選出候選輪廓線，用初步擬合的直線角度進行分類，然后對分類后的直線集合重組，并用優化的最小二乘法對其進行擬合得出直線特征。

本文提出的直線檢測算法具有良好的抗干擾性和適用性，相對于傳統的直線擬合算法，在復雜的圖像背景下，擬合結果更貼近實際直線。 此算法適用于多種工業場景下產品的直線特征提取，以對產品進行準確的定位。