面向邊緣協作的動態服務配置與遷移機制研究

杜 楚 ，黃澤鋒，李小翠

(1.中國電子科技集團公司第五十四研究所，河北 石家莊 050081；2.河北省智能化信息感知與處理重點實驗室，河北 石家莊 050081；3.中國地質大學(北京)信息工程學院,北京 100083)

0 引言

近年來，物聯網設備的普及催生了許多新興物聯網應用，如智能家居、智慧城市、實時制造和患者監測等。這些物聯網應用通常表現出嚴格的服務質量(QoS)要求，如低延遲和低能耗等，對物聯網設備有限的資源與計算能力帶來了重大挑戰[1-3]。邊緣計算成為緩解新興物聯網應用低延遲要求和設備資源受限之間沖突的首選平臺[4-6]。邊緣計算支持在靠近終端用戶的邊緣服務器上配置服務，用戶可以將復雜的計算任務卸載到附近的邊緣服務器，實現快速響應和實時計算任務處理[1]。因此，在邊緣計算下，服務實時配置到距離終端用戶最近的邊緣服務器上的同時，滿足用戶請求約束的QoS是一個關鍵挑戰。此外，當終端用戶請求的服務未配置在請求的邊緣服務器上時，為保證QoS，考慮將用戶任務通過當前請求的邊緣服務器遷移到臨近的邊緣服務器運行，或將臨近邊緣服務器上配置的服務動態遷移到當前邊緣服務器。因此，利用邊緣服務器之間協作，動態服務配置與遷移機制研究對于邊緣計算下減少用戶請求服務訪問延遲和降低設備能耗開銷至關重要。

邊緣計算下的任務動態配置和遷移受到了廣泛關注。許多研究者致力于設計有效算法來提升QoS和降低成本。任務分配決策在服務配置中起著關鍵作用，Chen等[7]通過對各參數的聯合優化，設計了一種能量最優動態計算卸載方案。文獻[8]為了最小化任務的卸載時間，設計了一種基于延遲依賴的優先級感知任務卸載策略，根據任務的截止時間為每個任務分配優先級。文獻[9-12]集中于部分卸載策略或協同優化卸載決策和資源配置。大多數相關研究只關注任務卸載以解決延遲和能耗限制，而忽略了用戶的服務請求在實際情況下是高度動態的。邊緣節點可能沒有配置任務所需的服務，這會限制任務卸載策略。考慮服務請求的多樣性與邊緣節點有限的服務數量之間的沖突，文獻[13]提出將服務從云遷移到網絡邊緣。但是，云服務器和邊緣節點之間通信的時間和能源成本很高。因此，頻繁地從云到邊緣節點的服務遷移會導致延遲和能耗增加。文獻[14]提出在邊緣節點之間遷移服務，使可用服務更接近用戶設備，減少服務遷移的額外成本。文獻[15]解決了何時何地遷移服務以在QoS和遷移成本之間實現最佳權衡的挑戰。文獻[16-18]側重在動態網絡環境中實現低延遲服務遷移和無縫計算。任務卸載和服務遷移問題可以建模為馬爾可夫決策過程(MDP)，利用強化學習算法獲得MDP的最優策略。

邊緣節點之間的協作(例如任務卸載和遷移)降低了設備的能源消耗，提高了QoS約束。以上研究大多數分別考慮這2種協作策略，并沒有將服務配置和遷移有效地結合起來。因此，本文提出了一種高效的計算任務卸載策略，將任務卸載與服務遷移策略動態結合，以最小化任務處理成本。本文的主要貢獻包括以下3點：

① 基于現實的任務請求模式與任務協作處理方式，分析了若干種任務請求模式的特征，歸納出多種請求情況，并制定了相應的遷移和卸載策略。

② 提出一種新的邊緣協作策略，在考慮傳統的縱向遷移和橫向卸載協同方式的同時引入服務橫向遷移的方式，并行執行任務卸載和服務遷移過程，減小了數據傳輸延遲，達到網絡整體能量消耗及響應延遲的最小化。

③ 通過對多種請求場景的分析，將選擇任務執行地點問題建模成多維馬爾可夫決策過程，利用深度強化學習算法并合理設置該算法的狀態空間、動作空間和獎懲函數等屬性，實現該問題快速決策。

為了評估該策略的可行性及高效性，本文對所構建的邊緣計算網絡下的任務協同處理問題進行了模擬仿真實驗。實驗結果表明，本文提出的策略可以有效地降低網絡整體延遲以及能量損耗。

1 相關工作

1.1 邊緣計算下的任務卸載

任務服務配置決策在邊緣計算中起著關鍵作用。通過對各參數的聯合優化，文獻[7]提出了一種能量最優動態計算卸載方案。考慮各個邊緣節點的能量效率和優先級，提出了公平任務卸載方案[9]。文獻[10]引入了一種新的動態邊緣計算模型，并設計了一種在線原對偶算法來卸載到達的任務。為了提高卸載算法的泛化能力，文獻[11]提出了一種基于元強化學習的任務卸載方法。考慮邊緣節點資源受限，文獻[12]提出了一種資源感知自適應任務卸載框架，靈活選擇最優卸載策略。

但是，這些算法沒有考慮到用戶請求的服務可能沒有在執行節點上配置。這項工作引入了一種動態計算卸載策略，將具有豐富計算資源的中間節點作為任務的執行節點。如果執行節點沒有配置相應的服務，服務遷移過程并行進行。本文采用深度強化學習算法快速決策最優中間節點。

1.2 邊緣計算下服務遷移

邊緣節點有限的服務和用戶時延敏感約束給邊緣計算下開展服務配置與遷移帶來了更多的挑戰。為了實現低延遲和無縫計算，邊緣節點間的服務遷移備受關注。文獻[16]提出了一種基于用戶活動熱點的服務遷移策略，根據用戶活動熱點圖，提前在邊緣節點上部署服務。文獻[17]開發了一種基于松弛和舍入的最優迭代求解方法來最小化遷移成本。文獻[14]將服務遷移問題表述為非線性 0-1規劃問題，并設計了基于粒子群的服務遷移方案。然而，由于傳統啟發式算法時間復雜度高，難以實現算法的快速收斂。強化學習正在成為優化服務遷移策略的一種有前途的方法，文獻[18-20]提出了服務遷移的決策過程建模為一維馬爾可夫決策，以服務遷移延遲為目標函數，提出利用強化學習優化服務遷移決策，實現算法快速收斂，有效地減少遷移過程中的額外延遲和能量消耗。

綜上所述，這些方法在特定的場景下節能效果十分顯著，但是并不適用于本文的場景。因此，本文提出了一種高效的計算任務卸載策略，采用深度強化學習實現快速決策，并將服務遷移與任務動態卸載相結合。

2 網絡和性能模型

本節介紹了系統模型，包括網絡模型、能耗模型和時延模型3個部分。

2.1 網絡模型

網絡基本要素主要包括邊緣節點的描述、服務和任務描述以及時間片的劃分，具體的定義如下：

① 該研究場景中，網絡包括N個邊緣節點，將這些邊緣節點表示為集合F={F1，F2，…，Fi，…，FN}。對于這些邊緣節點，通過以下幾個屬性來描述：邊緣節點的唯一標識Fi.id、邊緣節點的地理位置Fi.Loc=(Lx,Ly)、邊緣節點當前托管的服務列表Fi.HostLst、邊緣節點當前正在處理的任務列表Fi.PT以及處理器頻率Fi.Fre。其中，i∈[1,N],Lx為邊緣節點地理位置的經度，Ly為邊緣節點地理位置的緯度。不失一般性的前提下，本文考慮所有邊緣節點的資源相同，資源包括CPU處理能力、帶寬、內存和存儲。

② 本文網絡中包括了M種類型的服務，將這些服務類型標記為集合S={S1，S2，…，Si，…，SM}，并通過以下幾個屬性來描述：服務的唯一標識Si.id，服務的大小Si.Bytes和服務重配置所需的時間Si.RCT，其中，i∈[1,N]。服務重配置所需的時間與服務本身所占用的大小無直接關系。

③ 將時間段T均勻地劃分為相等的時間片，將其標記為T={T1，T2，…，Ti，…，Tt}。

④ 每個時間片下，假定用戶會發出K個任務請求，將其標記為C={C1，C2，…，Ci，…，CK}。對于這些任務請求，通過以下幾個屬性來描述：任務請求的地理位置Ci.Loc=(Lx,Ly)，任務請求的類型Ci.Sj，任務請求的數據量大小Ci.Bytes以及任務處理所需的CPU時鐘周期Ci.Cir。其中，i∈[1,N]，j∈[1,M]，Lx為發出請求的用戶的經度，Ly為發出請求的用戶的緯度。

2.2 能量模型

對于每個任務請求，其所需的總能耗為：

Etotal=Ecomp+Etti+Eftji，

(1)

式中，Ecomp為該任務的計算處理能耗；Etti為任務卸載到邊緣節點Fi的能耗；Eftji為服務從邊緣節點Fj遷移到邊緣節點Fi的能耗,i∈[1,N]，j∈[1,M]。

通信能耗模型的參數及其相關參數如表1所示。Etti和Eftji都是通信時將數據包從i點發送到j點產生的能耗，根據FORM模型，對于kbyte從節點發送到距離為d的節點的過程,，可以表示為：

Ecmm,ij(k,d)=ETx(k,d)+ERx(k)，

(2)

ETx(k,d)=Eelec×k+εamp×k×dn，

(3)

ERx(k)=Eelec×k，

(4)

式中，ETx(k,d)為將數據大小為k的數據轉發到距離為d的節點所消耗的能量；ERx(k)為接收kbyte數據所消耗的能量。傳播衰減指數n的值受環境影響較大。若設備之間傳輸數據時沒有建筑物遮擋，可將n的值設置為2，否則根據具體的環境可設置為3，4或5。Eelec和εamp分別表示單位能耗常數和發射放大器單位能耗常數。

表1 一階無線電模型參數

2.3 時延模型

對于每個任務請求，其所需的總延遲為：

Dtotal=Dcomp+max(Dtti,ArgMin{Dfttji}+Dr)+Dw,

(5)

式中，Dcomp為該任務的計算處理時間；Dtti為任務轉發卸載到邊緣節點Fi的時間；Dftji為服務從邊緣結點Fj遷移到邊緣節點Fi的時間；Dr為服務的重配置時間；Dw為任務請求處理的等待時間，i∈[1,N]，j∈[1,M]。Dttti和Dfttji都是通信時將數據包從i點發送到j點產生的時延，本文將無線傳輸時的延遲定義為：

delay=knetlgdij+bnet,

(6)

式中，dij為i點與j點的距離；knet和bnet定義如下：

knet=44.9-6.55lg(hb)，

(7)

bnet=46.3+33.9lg(f)-13.82lg(hb)-ahm+cm，

(8)

式中，f為信號頻率，單位MHz；hb為節點的天線高度；cm在一般情況下設置為3 dB;ahm定義如下：

ahm=3.20(lg(11.75hr))2-4.97，

(9)

式中，hr為用戶設備的高度。單個任務的計算時延Dcomp定義如下：

(10)

式中，C.Cir為任務處理所需的CPU時鐘周期；F.Fre為邊緣節點的處理器頻率。

2.4 目標函數定義

整個網絡的能耗和延遲成本定義為所有任務的能量消耗之和以及所有任務的時延之和的加權和，目標函數定義如下：

(11)

式中，Ditotal為所有任務請求完成所需的時延總和；Eitotal為所有任務請求完成所需的能量總和；ω1和ω2分別是控制權重的參數。

3 基于DQN服務配置與遷移

在強化學習算法中，對于每個時間片Tτ，產生系統狀態Sτ，并計算上一時刻的獎勵Rτ-1。根據預先定義的策略選擇動作Aτ。執行該操作后，系統將在下一個時間片中轉換到新狀態Sτ+1。同樣，再次計算獎勵Rτ并根據狀態Sτ+1選擇新動作Aτ+1。

3.1 服務配置狀態空間

系統狀態基于延遲、能耗、邊緣節點托管的服務類型、邊緣節點的運行狀態以及當前時間片的所有請求信息。系統總延遲和總能耗如下：

(12)

即，Xi,j(t)為t時刻，請求i在邊緣節點Fj上執行的總延遲Dtotal。

(13)

即，Yi,j(t)為t時刻，請求i在邊緣節點Fj上執行的總能耗Etotal。

綜上所述，系統在t時刻的狀態可以表示為：

St={X(t),Y(t),F.HostLst,F.rt,C.Loc,Ci.S}∈S，

式中，S為系統的狀態空間。

3.2 服務遷移動作空間

動作空間被定義為等待處理的任務請求的候選執行地點集，即所有的邊緣節點集合以及云節點，系統Tτ時刻的動作可以表示為一維向量：

At= {aF1,aF2,…,aFN,ac}∈A，

式中，A為所有可執行的動作，每一個元素值代表了該請求是否在此處執行，其值為1時代表在此處執行，其值為0時代表不在此處執行；Fi為邊緣節點；c為云節點。

3.3 服務配置與遷移獎懲函數

本文的目標是最小化延遲和能耗，因此，系統Tτ時刻的獎勵定義為：

Rt=M1-(Dtotal(t)+Etotal(t))，

(14)

式中，M1為常數值；Dtotal(t)，Etotal(t)分別表示時刻t產生的任務請求的處理延遲以及能量損耗。

3.4 服務配置與遷移算法設計

本文采用了DNN和 Q-Learning相結合的深度Q-Learning算法。在深度Q-Learning算法中，使用Q-Network存儲Q矩陣，該網絡由權重為θ的DNN組成，可以有效存儲Q值信息。算法1描述了深度Q-Learning算法。對于每次迭代，首先獲取初始狀態S0，對每個時間片τ，根據預先定義的策略選擇動作Aτ，并獲取下一個狀態Sτ+1。通過式(14)計算獎勵，更新Q-Network并最終輸出動作Aτ。

算法 1:基于服務遷移和邊緣協作的DQN算法輸入:θ:Q-Network的權重D:經驗重放池輸出:Aτ:動作算法流程:1:for episode = 1,M do2: 獲取初始狀態S03: 初始化D3: for τ= 1,k do4: 調用算法2選擇動作Aτ 5: 獲取狀態Sτ+16: 通過式(14)計算Rτ7: 調用算法3,根據Sτ,Sτ+1,Aτ,Rτ,D更新Q-Network8: 輸出動作Aτ9: end for10:end for

3.4.1 動作選擇

動作選擇基于epsilon-greedy策略，該算法主要包括2個部分：探索者及開發者。預設一個ε閾值，每次選擇時產生一個隨機值Φ，當Φ大于ε，則由開發者進行動作選擇；否則通過探索者進行動作選擇。具體動作選擇過程如算法2所示。

算法 2:動作選擇輸入: Sτ:當前狀態 BD:最佳動作表輸出: Aτ:動作算法流程: 1:產生隨機值Φ 2:ifΦ>εthen 3: 通過開發查找最佳動作表BD,得到Aτ 4:else 5: 獲取可用計算資源列表L 6: 從資源列表中隨機選取邊緣節點Fi,得到對應的Aτ 7:end if

3.4.2 Q-Network更新

在Q-Learning算法中，每個Q(Sτ-1，Aτ-1)都可以用如下規則更新：

Q(Sτ-1,Aτ-1)←(1-α)Q(Sτ-1,Aτ-1)+

α[Rτ-1+γ×maxAτQ(Sτ,Aτ)，

(15)

式中，α為學習率；γ為折扣率。在深度Q-Learning算法中，Q值信息一般都被抽象存儲在DNN中，由于系統狀態會在每個時刻Tτ不斷變化，因此DNN需要自適應地進行更新。目標網絡提供穩定的Q(Sτ，Aτ;θ’)，其y(τ)定義如下：

yτ=E{(1-α)Q(Sτ-1,Aτ-1;θ′)+

α(Rτ-1+γmaxQ(Sτ,Aτ;θ′))}，

(16)

式中，θ′為目標網絡的權重，會間歇地重置回θ。

算法3描述了Q-Network更新過程。在該算法中，對于每個時刻，都將經驗四元組(Sτ，Aτ，Rτ，Sτ+1)存儲在經驗重放池D中，然后在D中抽取一組四元組用于更新網絡。對于每個四元組(Sτ-1(j)，Aτ-1(j)，Rτ-1(j)，Sτ(j))，計算Q(Sτ(j)，Aτ(j);θ’) 和y(τ)。

3.5 服務配置與遷移算法復雜度分析

在算法1中，算法時間復雜度主要包括動作選擇算法和Q-Network更新算法。其中，對于行2及行5的狀態觀察和收集，其時間復雜度與需要收集的狀態的個數有關，即邊緣節點的個數N，對于K個任務請求，需要預計每個任務請求在各個邊緣節點上運行的延遲和能耗，因此該步驟的時間復雜度為O(K×N)。對于行4，其時間復雜度取決于動作選擇算法，開發過程只需要查找最佳動作表，因此時間復雜度為O(1)，探索過程需要在可用資源列表中隨機選擇動作，在3.3節已經分析過該步驟的時間復雜度為O(N)。對于行6，其時間復雜度取決于獎勵函數的計算，具體為O(N+M+K)。對于行7，其時間復雜度取決于Q-Network的更新，其時間復雜度取決于經驗重放池D的大小，大小取決于狀態空間S的大小和動作空間的大小A，狀態空間大小為邊緣節點和云節點的個數之和N+1，動作空間大小一般情況下為邊緣節點的個數N，故可得該算法時間復雜度為O(N2)。

4 結果評估

實驗程序的運行環境為：64位Windows10操作系統、16 GB內存、處理器為Intel(R) Core(TM) i7-3770 CPU @ 3.40 GHz以及顯卡NVIDIA GeForce GTX 1070 Ti，通過Python程序實現。為保證實驗的科學性，所有實驗均在同一環境下進行。

4.1 實驗設置

本實驗中的參數設置如表2所示。

表2 實驗參數設置

網絡區域為500 m×500 m，該區域中均勻分布了50個邊緣節點。由于邊緣節點的資源限制，每個邊緣節點上最多可配置H=2種服務。通常一個物聯網部署之后，會根據節點的部署情況，選擇一個合適的通信范圍，為了保障該網絡的連通性，本文將邊緣節點的通信半徑設為150 m。邊緣節點的CPU頻率F.Fre=2 GHz。任務處理所需的CPU時鐘周期C.Cir∈[50,200]單位時間。信號頻率f=2.5 MHz，天線高度hb=35 m，用戶設備高度hr=1 m。無線信號傳輸的帶寬wi=500 MHz，無線傳輸的能量消耗常數Eelec=50 nJ/bit，傳輸放大器的能耗常數εamp=0.1 nJ/(bit·m2)。CPU單循環的計算能耗為6×10-9Wh。成本函數的時延權重ω1=0.8，能耗權重ω2=0.2。

對于DQN中的網絡參數設置，學習率α=0.1，折扣率γ=0.9。對于DNN的結構，本文使用4層全連接層的神經網絡，該網絡的設置基于實驗結果。本文對網絡的深度設置開展了大量實驗，結果表明，4層的網絡在本文的問題場景以及數據下有較好的表現。本文將狀態St和動作At對表示為元組，并轉換成12 127×1的向量，將其作為DNN的輸入。在DNN的第1層和第2層之間添加了線性整流激活函數。DNN的輸出則是St和At元組的Q值對。需要注意的是，在該網絡中，所有的邊緣節點有著相同的DNN結構和權重。

4.2 實驗結果

本實驗通過觀察系統長期的平均延遲以及能耗來探索不同的系統參數設置對該策略的影響，這些系統參數包括任務請求的稀疏度以及服務類型的個數。

4.2.1 任務請求稀疏度

當任務請求的稀疏度越高，平均每個時刻產生的任務請求會越多，則系統的平均響應延遲以及能耗會越高。為了研究任務請求的稀疏度對平均延遲和能耗的影響，本文實驗將任務請求的稀疏度prob設置為0.2，0.4,0.8。不同任務請求稀疏度設置下系統平均延遲如圖1所示。

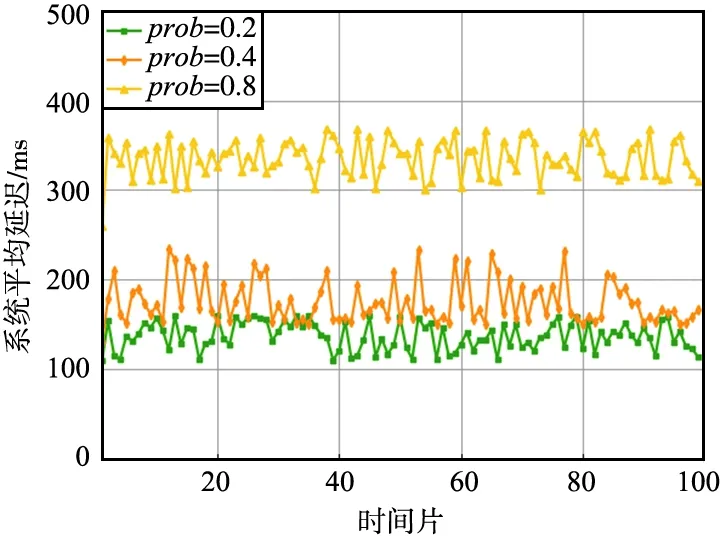
圖1 不同任務請求稀疏度設置下系統平均延遲Fig.1 Average system delay under different task request sparsity settings

系統的平均響應延遲與每個時刻的任務請求數量成正比，即與任務請求的稀疏度成正比，但從圖中可以觀察發現，稀疏度prob=0.4時，相比于稀疏度prob=0.2時的系統平均延遲沒有增加至一倍，其原因是prob=0.2時，在密集部署邊緣節點的網絡中，該網絡的計算負載是不飽和的，因此接收到任務請求時，邊緣節點往往可以立即處理該任務請求。而稀疏度prob=0.4時，該網絡的計算負載接近飽和，此時任務請求開始出現不能在最合適的邊緣節點上立即處理的情況，邊緣間協同處理情況開始變得頻繁。prob=0.8時，該網絡的計算負載過飽和，因此平均延遲相比于稀疏度prob=0.4時翻倍。

不同任務請求稀疏度設置下系統平均能耗如圖2所示。直覺上，系統的平均能耗與每個時刻的任務請求數量成正比，即與任務請求的稀疏度成正比，因為無論系統是否處于飽和的狀態，任務請求是否由于計算資源不足導致延遲增加都與能量損耗沒有直接關系。由圖2可以看出，當系統計算負載接近飽和時，開始出現較頻繁的服務遷移和任務卸載，這些任務協同處理方式必然會導致傳輸能耗增加，因此，系統的平均能耗與任務請求的稀疏度成線性增加的關系。

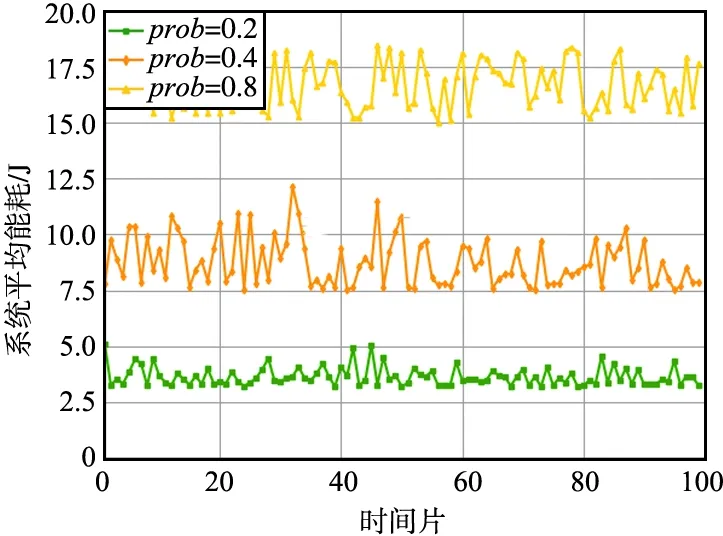
圖2 不同任務請求稀疏度設置下系統平均能耗Fig.2 Average system energy consumption under different task request sparsity settings

4.2.2 服務類型的個數

不同服務類型數量設置下系統平均延遲如圖3所示。

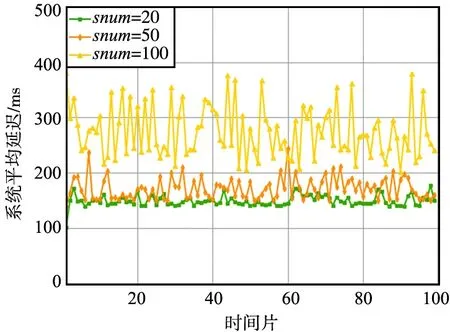
圖3 不同服務類型數量設置下系統平均延遲Fig.3 Average system delay under different service types and quantity settings

服務類型數量snum=50時，系統的平均延遲與圖3中prob=0.4的系統平均延遲基本一致。當snum=20時，所有服務類型都可以在邊緣網絡中找到多個配置了該服務類型的邊緣節點，因此服務遷移和任務卸載的地點有了更多候選，也更容易找到與數據產生地點鄰近的任務處理地點。因此，在邊緣網絡的計算負載還沒有完全飽和時，隨著服務類型snum值減小，系統的平均響應延遲也越小。值得一提的是，當snum=100時，系統平均延遲的波動率顯著增加，分析這一現象可能的原因是邊緣層配置的服務出現了“脫靶”的情況，即任務請求的類型可能在邊緣層級上沒有找到配置了相應服務的邊緣節點，配置了相應服務的邊緣節點計算資源不足或者其物理距離不夠鄰近也可能造成該問題。在這種情況下，邊緣節點為保障任務能有效處理，必須將任務卸載至云端或者將云端中的服務類型遷移至邊緣層，這種遠距離的遷移或者卸載都會導致任務的響應急劇增加，從而出現了圖中系統平均延遲波動率增加的情況。因此，當服務類型數量遠多于邊緣層所能配置的服務數量時，為盡量減少脫靶的情況，如何對邊緣層的服務進行合理的預配置，以及在遷移時如何保證邊緣層服務的豐富度是亟需研究的問題。

不同服務類型數量設置下系統平均能耗如圖4所示。

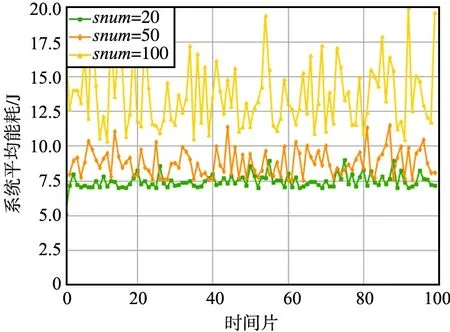
圖4 不同服務類型數量設置下系統平均能耗Fig.4 Average system energy consumption under different service types and quantity settings

由圖4可以看出，相比于系統平均延遲，服務類型數量snum=100時，邊緣網絡的系統平均能耗波動率更大。如圖4所示，波動率增大的原因是發生了脫靶情況，這種情況導致邊緣節點不得不進行遠距離的遷移和卸載，但受益于第3節提出的圍繞計算資源的策略，邊緣節點在任務處理時是將可用的計算資源作為遷移和卸載的中繼點，并通過服務遷移和任務卸載使其存在時間、空間上重疊，因此該策略在發生遠距離邊緣間協作時，可以有效降低任務處理的延遲，但是邊緣節點的數據量傳輸的距離沒有太多變化，因此相比于系統平均延遲，系統的平均能耗在脫靶時代價更大。

5 結束語

針對服務請求高度多樣且動態變化的情況，如何對計算、存儲和帶寬等資源限制的邊緣節點實時服務配置與遷移，使網絡的總體能耗以及請求延遲盡量最小化，本文提出了一種基于服務遷移和邊緣協作的服務動態重配置策略，降低任務請求處理過程中的時延以及能耗。根據所提策略設置深度強化學習算法的狀態空間、動作空間和獎勵函數，并利用深度強化學習進行任務處理地點的決策，解決傳統啟發式算法由于復雜度過高無法在時延敏感的場景中使用的問題。為了驗證本文提出策略的可行性和高效性，探索了2種不同的網絡參數因子對該策略的影響，并且對比了2種傳統的任務協作處理方式，實驗結果表明，本文所提策略可有效降低系統任務處理延遲，并且一定程度上可以減小系統能耗。