含恒功率負載的直流微網穩定性分析

劉海濤 ，熊 雄 ，徐旖旎 ，張 海 ，邵 瑤

（1.國網上海能源互聯網研究院有限公司，上海 201210；2.中國電力科學研究院有限公司，北京 100192）

隨著可再生能源和電力電子負載的發展，直流微網以其轉換次數少、控制結構簡單、不需要對電壓的相位和頻率進行跟蹤等優點，成為未來家庭、樓宇和社區的主要供電架構[1]。然而，直流微網中包含恒功率負荷CPL（constant power load），電壓變化時呈現負阻抗特性，極易引起母線電壓振蕩甚至崩潰，因此穩定性分析是直流微網研究中的核心問題之一[2]。

直流微網系統穩定性分析主要涉及靜態穩定分析、小擾動穩定分析和大擾動穩定分析3個方面。靜態穩定分析主要研究系統是否存在穩態工作點，是小擾動和大擾動穩定分析的基礎。小擾動穩定分析則通過建立直流微網系統的小信號模型，利用Middlebrook阻抗比判據或特征值分析法對直流微網系統的局部穩定性進行分析[3-6]。前者是通過設定不同的穩定裕度和禁止區，基于阻抗比對直流微網進行小擾動穩定性分析的，其缺點是它規定了功率流向，但實際直流微電網中，有些微源如并網變換器或儲能單元既可以作為電源運行也可以作為負載運行，無法明確區分電源輸出阻抗和負載輸入阻抗[5]。特征值分析法通過判斷系統雅克比矩陣的特征值來判斷系統的小擾動穩定性，其對于功率流向沒有限制。文獻[6]運用該方法對直流微網系統的小擾動穩定性進行了分析，得到了系統小擾動穩定的判據，并探究了系統參數對穩定性的影響，但得到的穩定判據不僅與系統參數有關，還與由系統參數決定的系統的工作點有關，因而該穩定判據不能很好的指導直流微網系統的設計。

小擾動穩定分析只能研究直流微網系統的局部穩定性，但實際直流微網中，負載突變或母線電壓跌落等大擾動不可避免，因而對直流微網進行大擾動穩定分析，從全局角度評估系統穩定性十分有必要[4]。目前，較為成熟的非線性系統穩定性分析方法是李雅普諾夫直接法[7-10]。應用該方法的難點在于建立李雅普諾夫函數LF（Lyapunov function），目前已取得一些研究成果。文獻[8]提出Takagi-Sugeno（TS）模糊模型的穩定性分析工具，但利用該方法需要求解線性矩陣不等式，且其個數與非線性的數目滿足指數關系，因而計算比較復雜；文獻[9]提出通過平方和SOS（sum-of-square）規劃法構造系統的李雅普諾夫函數，但該方法是數值方法，當利用該方法分析參數對系統估計吸引域EDA（estimated domain of attraction）的影響時，參數每改變一次，就需要重新進行數值計算構造系統的LF，因而較難分析參數對EDA的影響；文獻[10]提出二次對角化LF（BDQLF）法，該方法利用非線性系統的線性化矩陣構造LF，并運用遺傳算法確定系統的EDA，但是遺傳算法編程實現復雜，且搜索速度慢，另外遺傳算法容易收斂到局部最優解，因而該方法計算復雜，EDA的保守性較強。

針對上述問題，本文從靜態穩定、小擾動穩定及大擾動穩定3個方面對含CPL的直流微網系統的穩定性進行了系統性分析，主要工作包括4個方面：①建立了直流微網系統的等效降階數學模型，并通過仿真軟件Matlab/Simulink對該等效降階模型的有效性進行了驗證；②分析了直流微網系統存在靜態工作點的條件，得到系統靜態穩定的判據，并在此基礎上，利用李雅普諾夫穩定性第一定理，得到了直流微網系統的小擾動穩定判據，為直流微電網系統的設計提供參考依據；③利用混合勢函數理論并結合LaSalle不變集定理得到了系統小擾動穩定平衡點的EDA；④對所得穩定性判據和EDA進行仿真驗證，證明了其正確性。

1 直流微網結構與數學模型

1.1 直流微網結構

直流微網系統通常包含儲能單元ES（energy storage）、分布式發電單元DGs（distributed generations）、并網變換器單元和負載單元等[5]。其中：儲能單元具有平衡功率的作用，可作為恒功率單元或電源運行，作為電源運行時源變換器采用電壓-電流下垂控制方式平衡母線電壓；DGs通常由再生能源構成，為最大限度利用可再生能源并考慮其波動性和間歇性，DGs常采用最大功率跟蹤控制策略，可看作CPL；并網變換器單元作為直流微電網與電網的接口可作為CPL運行或電源運行；負載單元包括直接接入母線的負載和通過變換器接入母線的負載，后者可看作CPL。本文選擇儲能單元作為電源，通過源變換器接入母線；恒功率單元由荷變換器連接可變電阻來表示，系統的具體結構如圖1所示，詳細系統參數見表1。

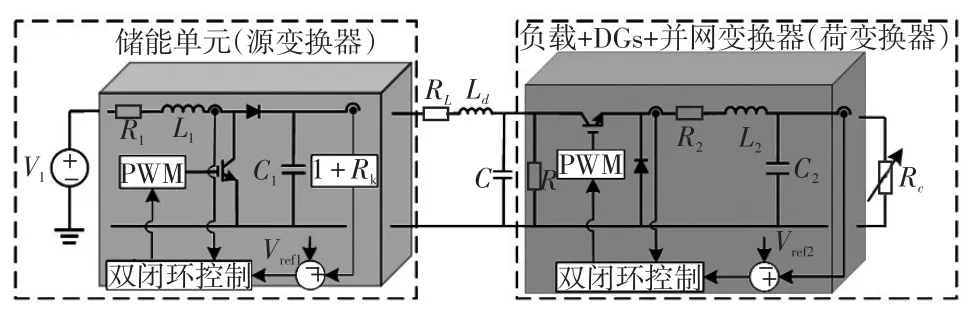
圖1 直流微網系統的拓撲結構Fig.1 Topological structure of DC microgrid system

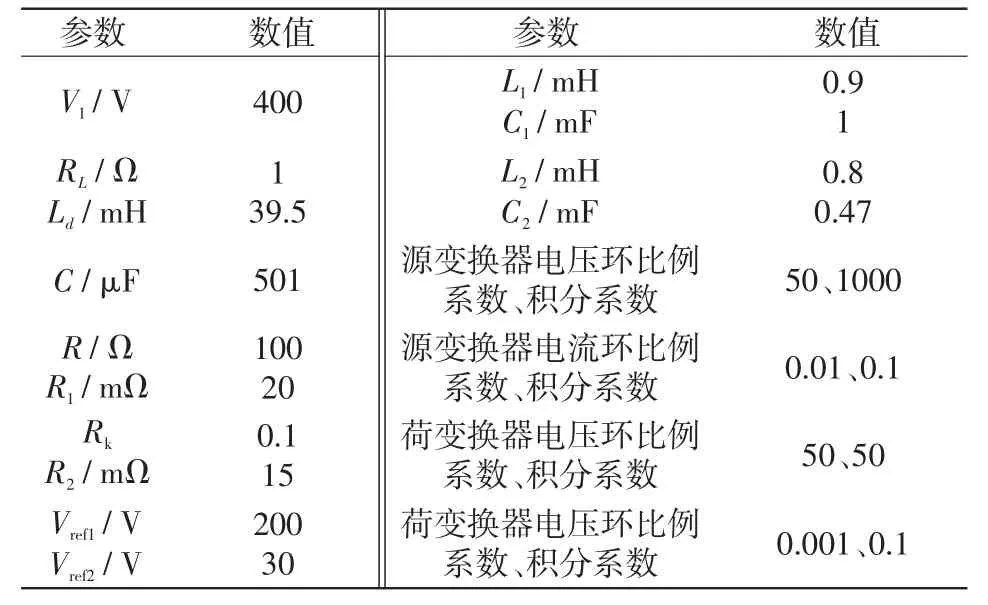
表1 直流微網系統的參數Tab.1 Parameters of DC microgrid system

1.2 直流微網的等效降階模型和模型驗證

忽略圖1中源、荷變換器的電壓電流控制動態，則圖1左側可等效為理想電壓源串電阻電路，右側可等效為CPL。因而圖1中的系統結構可以簡化為如圖2所示的等效電路模型，圖中：P為DGs、并網變換器單元和負載單元中CPL的功率之和；RL和Ld分別是線路電阻和電感，C是母線電容，R是負荷電阻，I是電感電流，V是電容電壓，Rk和Vref是源變換器電壓-電流下垂控制的下垂系數和參考電壓。

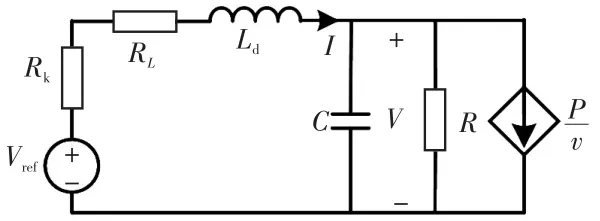
圖2 直流微網系統等效電路模型Fig.2 Equivalent circuit model of DC microgrid system

根據圖2所示，以I和V為狀態變量，系統的非線性降階數學模型可表示為

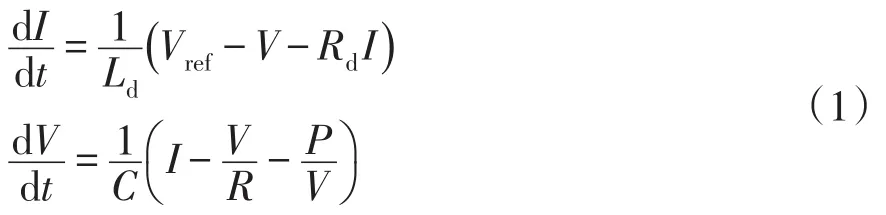
式中，Rd=Rk+RL。

式（1）即為本文分析的直流微網系統的等效降階數學模型。為驗證其正確性，在Matlab/Simulink中分別搭建如圖1所示的開關模型和等效降階數學模型，并做仿真驗證。

運行工況：t=3 s時功率P由300 W階躍到500 W，仿真結果如圖3所示。由圖3可見，暫態過程中，開關模型和本文所提的降階數學模型具有較好的擬合度，說明該降階數學模型可以較好地反映系統的暫態特性，驗證了降階數學模型的正確性。

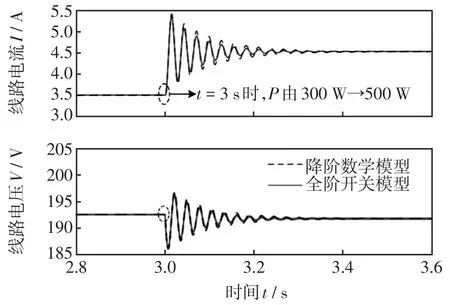
圖3 基于開關模型和數值模型的仿真結果對比Fig.3 Comparison of simulation result between switch model and numerical model

2 穩定性分析

直流微網系統的穩定性分析可分為3個步驟。

步驟1 靜態穩定分析。分析系統是否存在平衡點。

步驟2 小擾動穩定分析。分析系統的平衡點是否為小擾動穩定平衡點SEP（stable equilibrium point）。

步驟3 大擾動穩定分析。分析系統經受大擾動后的暫態過程的穩定性。

需要強調的是，上述步驟中，系統靜態穩定是進行步驟2的前提，系統小擾動穩定是進行步驟3的前提。

2.1 靜態穩定分析

系統的平衡點滿足系統狀態變量的導數等于0，故令式（1）左邊等于0，得系統的平衡點ei=[Ii,Vi]，其中Ii是系統第i個平衡點的電感電流分量，Vi是系統第i個平衡點的電容電壓分量。則有

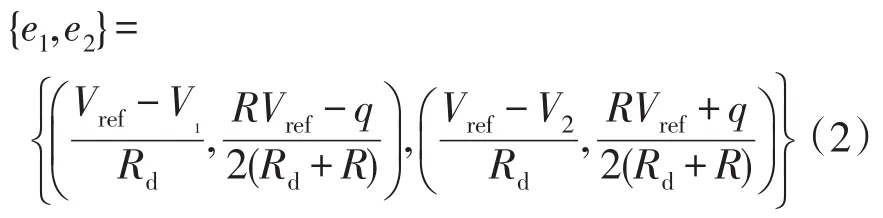
基于式（2）可知，系統靜態穩定的充要條件為

將式（3）中小于號右側式子記作P1。

由上述分析可知，功率P小于P1時系統存在2個平衡點，系統靜態穩定。

2.2 小擾動穩定分析

由李亞普諾夫穩定性第一法可知，如果系統平衡點的雅克比矩陣特征值的實部皆小于0，則該平衡點是小擾動穩定的[3]。本文利用該定理分析直流微網系統的平衡點e1和e1是否為SEP，或者在什么條件下是SEP，即系統小擾動穩定的判據。

對式（1）線性化，各平衡點的雅可比矩陣為

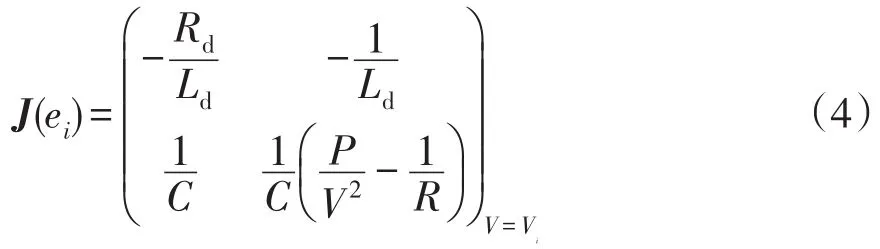
對于式（4），矩陣J(ei)的特征特征值λ1、λ2的實部小于0與λ1+λ2＜0且λ1λ2＞0等價。而λ1+λ2等于J(ei)的跡tr(J(ei))，λ1λ2等于J(ei)的行列式。因而可得

2.2.1 平衡點e1的小擾動穩定性

將式（2）的e1代入式（4）可得J(e1)，求其行列式得

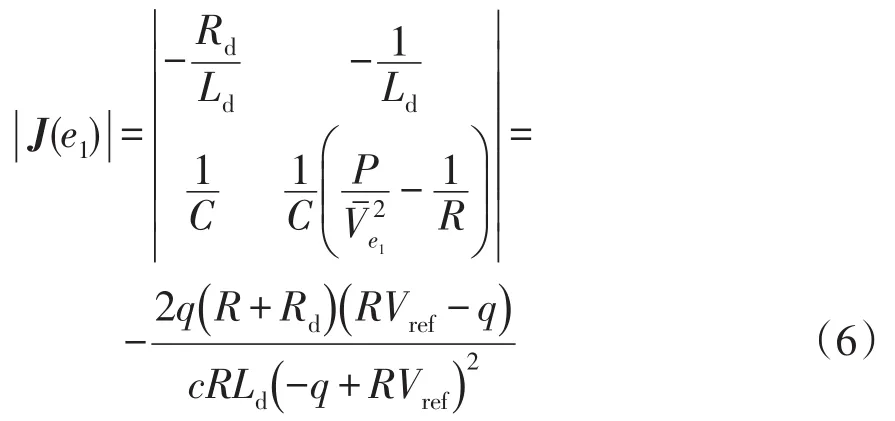
2.2.2 平衡點e2的小擾動穩定性

將式（2）的e2代入式（4）可得J(e2)，求其行列式得

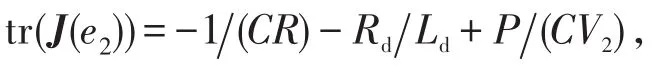
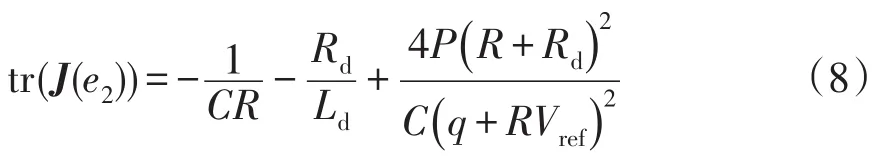
電容C取不同值所對應的2種情況討論tr(J(e2))與0的大小關系。

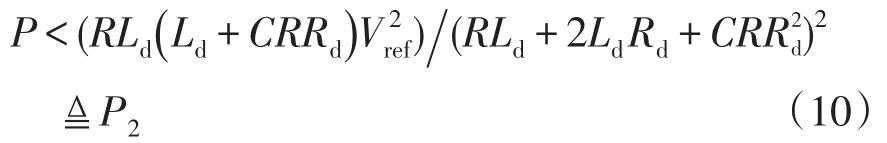
將式（10）小于號右側式子記作P2。

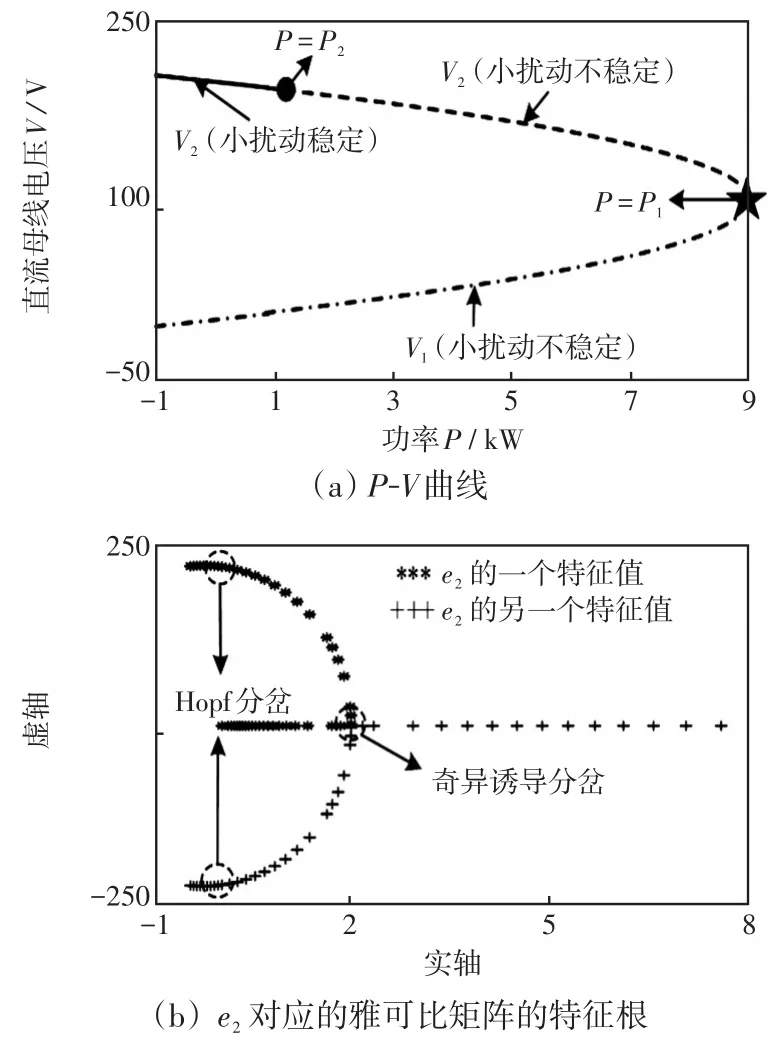
圖4 小擾動穩定分析示意Fig.4 Schematic of small disturbance stability analysis

2.3 基于混合勢函數法的大擾動穩定分析

本文將在系統小擾動穩定的基礎上，利用混合勢函數理論并結合LaSalle不變集定理給出直流微網系統小擾動穩定平衡點的估計EDA。

2.3.1 混合勢函數理論

Brayton和Moser基于基爾霍夫定律證明了對于非線性電路可以描述[11-12]為

式中：I為電感電流；V為電容電壓；L和C分別為電路中電感和電容組成的對角矩陣；P(x)為混合勢函數MPF（mixed potential function）的標量函數。文獻[11]給出MPF的一般形式為

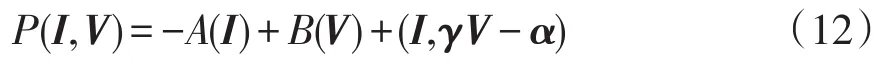
結合式（1）可得MPT對時間的導數為

由式（13）可知，如果電路中只有電感或電容，則-P（x）或P（x）對時間的導數小于0。這種情況可以運用李雅普諾夫穩定性定理判斷系統的穩定性。但通常情況下，電路中電感和電容是同時存在的，故P（x）對時間的導數不定[11]。為了解決這一問題，Brayton和Moser在R和LC中至少存在1類線性元件的假設下，給出了3種構造李雅普諾夫型能量函數LEF（Lyapunov-type energy function）的方法和3條相應的穩定性定理。其中第1、2條穩定性定理要求R線性，第3條穩定性定理則要求LC線性。本文分析系統的電感和電容是線性的，滿足第3條穩定性定理的假設條件，故本文運用該條定理分析直流微網系統的大擾動穩定性，為方便下文應用，現重述如下[11]。

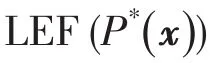
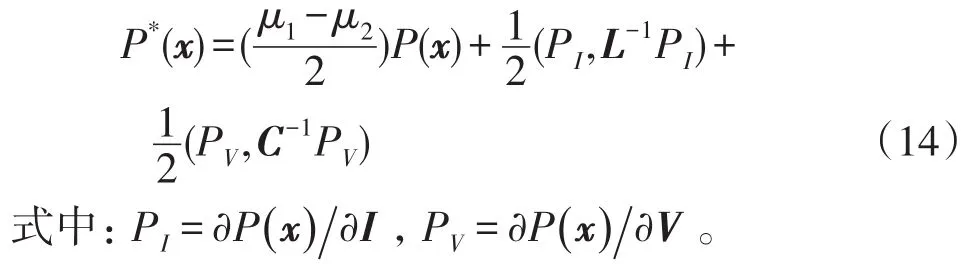
2.3.2 直流微網系統的MPF和LEF

選擇Γ的起始點和終點分別為圖2系統的穩態工作點(Ie,Ve)和任意點(I,V)。由于MPF與積分路徑無關，因而本文選取電流的方向作為積分路徑，因而直流微網系統的MPF為

式中：Ipe為CPL的穩態電流；等號右側各項依次為Rd、R、CPL和等效電壓源的電流勢函數以及電容支路的電壓和電流的乘積。化簡式（15）可得

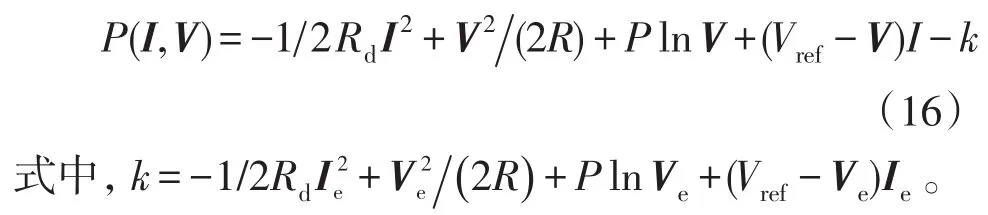
結合式（14）和式（16）可得直流微網系統的LEF為

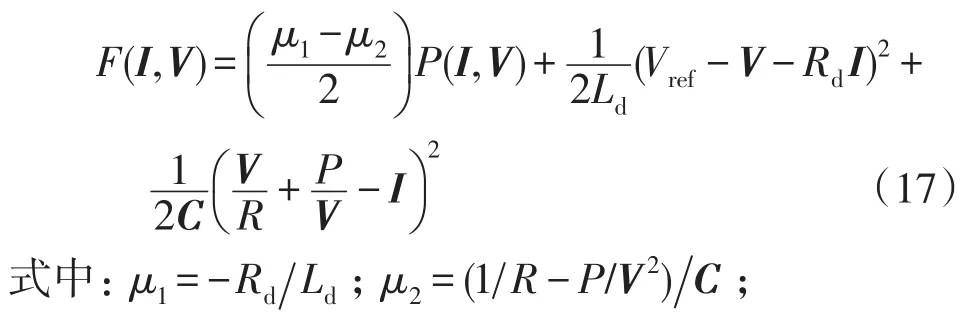
由μ1+μ2＞0可得到

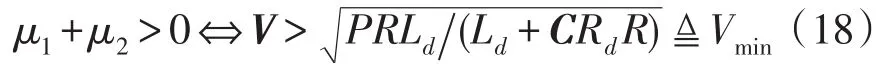
將式（18）大于號右邊的式子記作Vmin。

由MPT理論的第3條穩定性定理可知，當μ1+μ2＞0時，dF(I,V)/dt＜0成立。結合式（18）可知，當V＞Vmin時，dF(I,V)/dt＜0成立。

2.3.3 直流微網系統的估計吸引域

由上文分析可知，當V＞Vmin時，dF(I,V)/dt＜0成立，但F(I,V)的正定性仍不確定。不過LaSalle不變集定理并不要求F(I,V)正定，故本文運用該定理刻畫直流微網系統的EDA。LaSalle不變集定理介紹如下[13]。

（2）在Ωl內，所有x滿足dV(x)/dt＜0。則Ωl內所有使得dV(x)/dt=0的點的集合叫做K，M是K內的最大不變集。如果系統的初始點位于Ωl內，那么隨著t→∞，系統一定收斂于M中的點。

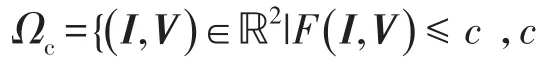
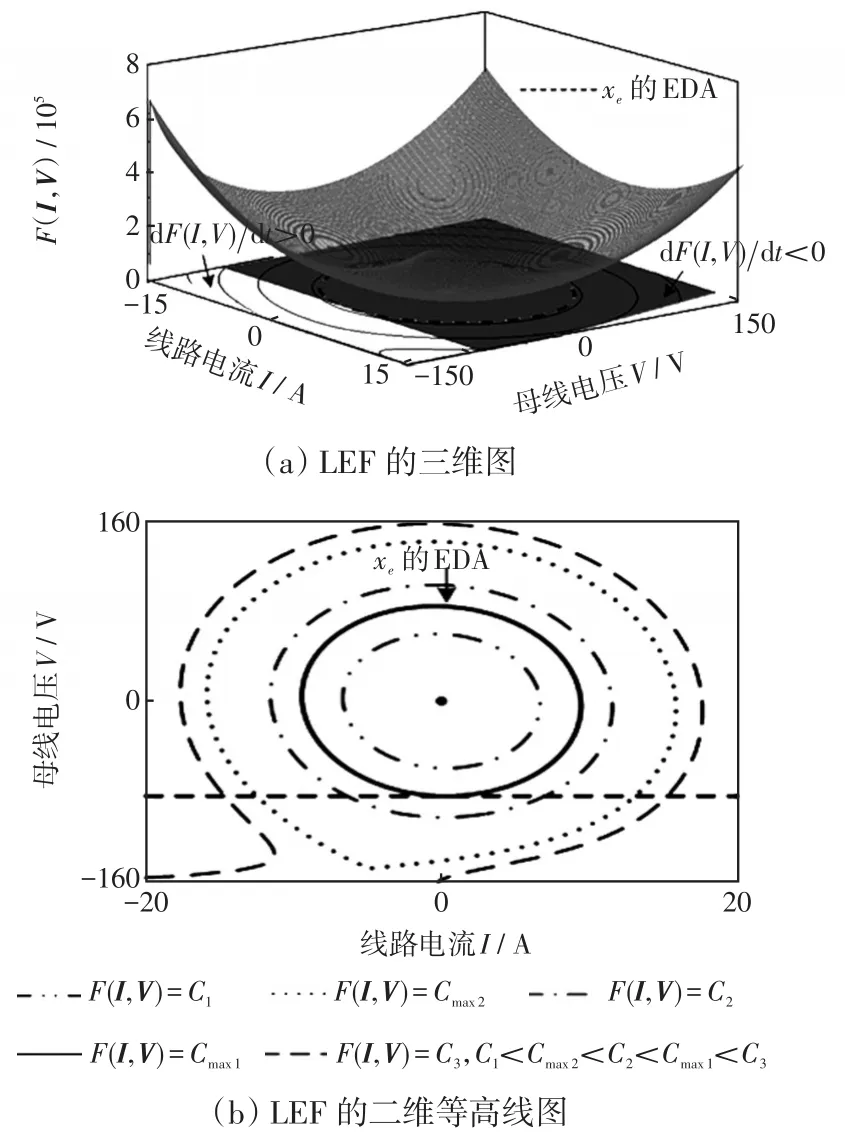
圖5 LEF的三維圖和二維等高線圖Fig.5 Three-dimensional plot and two-dimensional contour of LEF

根據圖5中LEF的等高線在狀態空間中圍成的區域隨LEF值的變化趨勢，結合LaSalle不變集定理可得直流微電網系統的EDA為

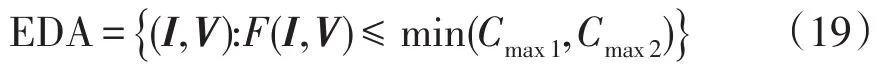
根據式（19），可得直流微網系統的EDA如圖6所示。EDA的含義是：如果系統的初始點在其內，則隨著t→∞系統一定收斂于xe。此外，為驗證該EDA的正確性，本文利用文獻[4]中的逆軌跡法，直流微網系統的真實吸引域邊界如圖6所示。由圖可見，該EDA在系統真實的吸引域邊界內，這說明本文所刻畫的EDA是正確的。此外圖6中灰色區域為利用MPT理論刻畫的EDA的保守性對應的區域。

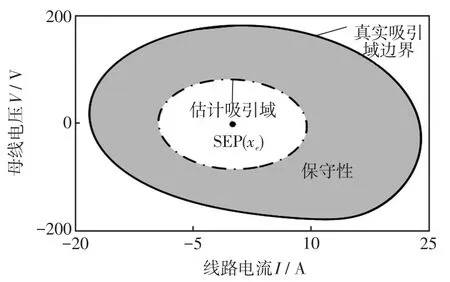
圖6 直流微網系統的吸引域和EDAFig.6 Domain of attraction and EDA of DC microgrid system

3 仿真分析

為驗證本文分析得到的靜態穩定判據（3），小擾動穩定判據式（9）和式（10）以及系統EDA式（18）的正確性，借助Matlab/Simulink對工況1～3進行仿真，如無特殊說明系統參數與表1保持一致。

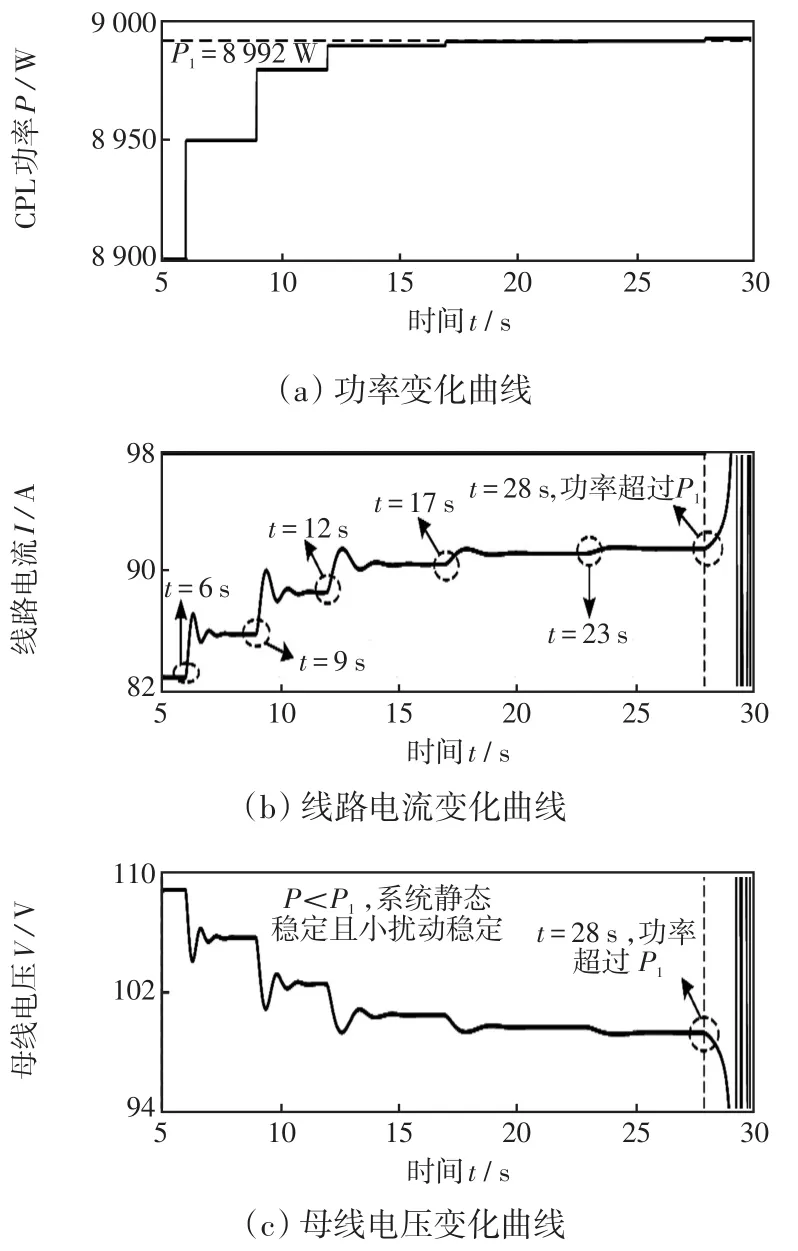
圖7 工況1的仿真結果Fig.7 Simulation results under working condition 1

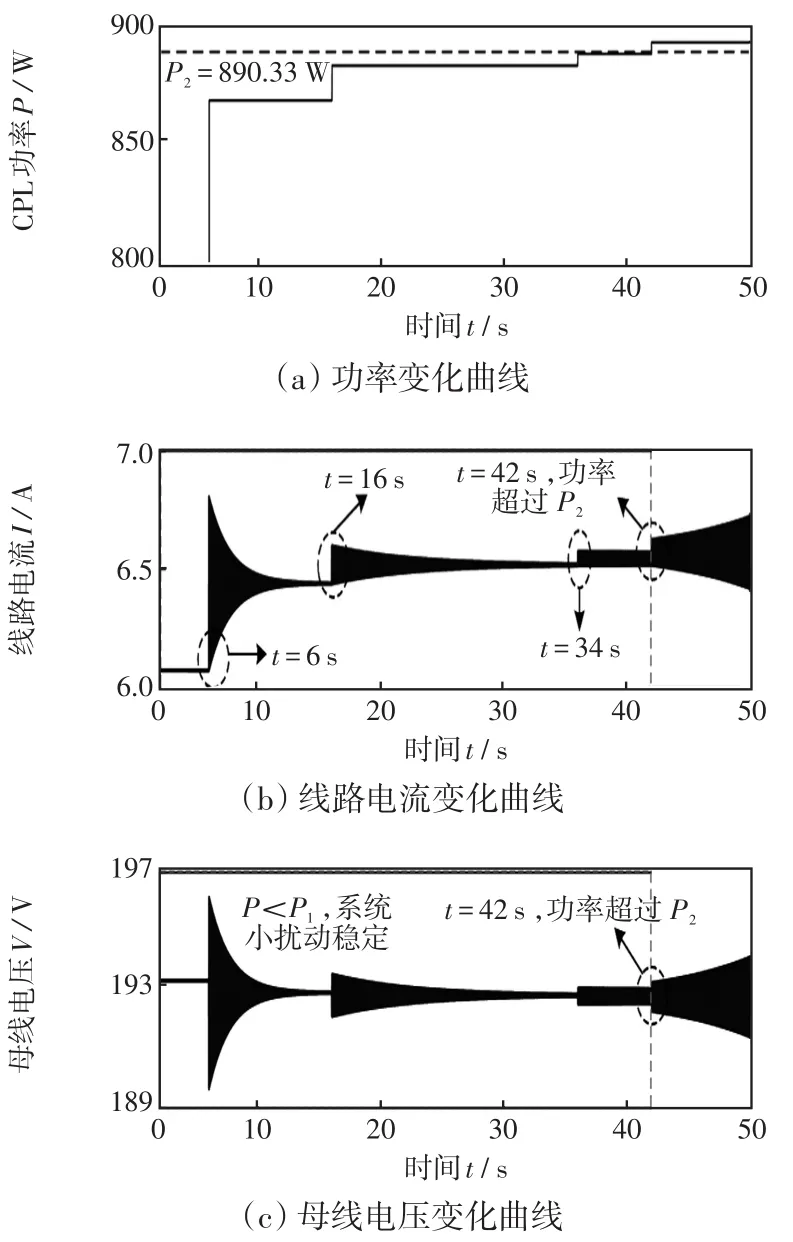
圖8 工況2的仿真結果Fig.8 Simulation results under working condition 2

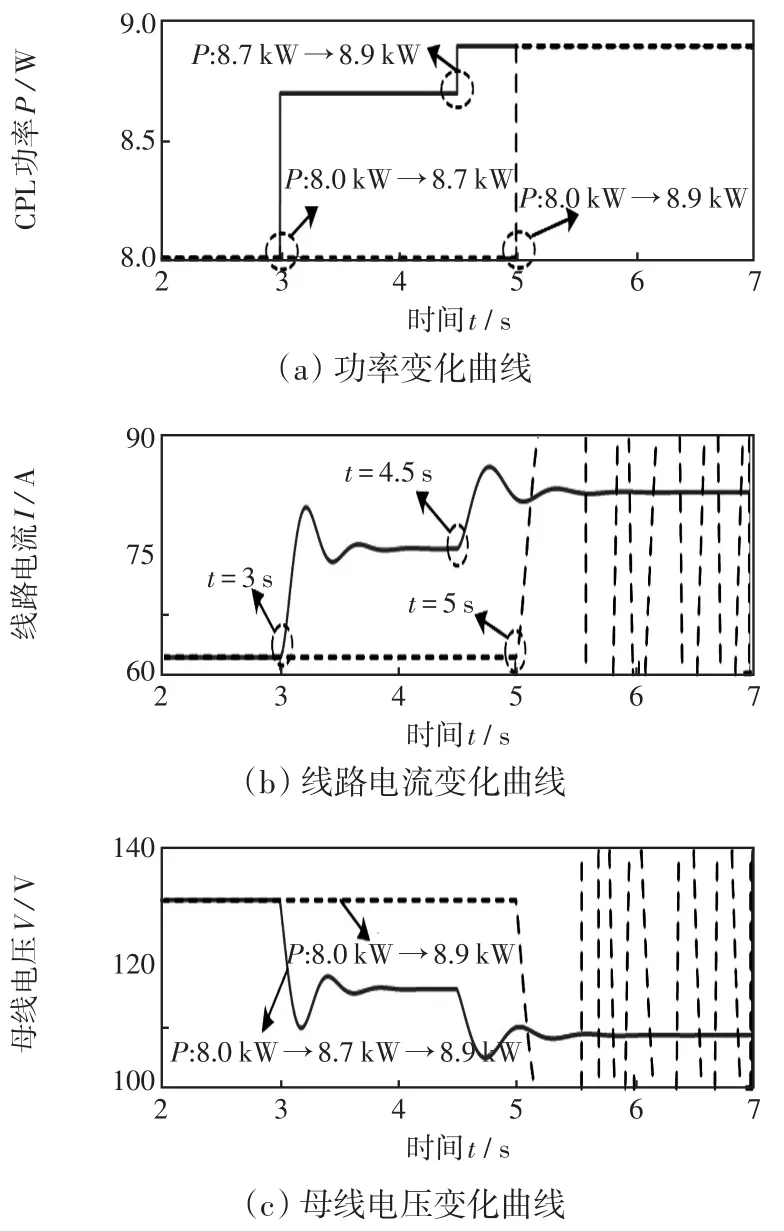
圖9 工況3的仿真結果Fig.9 Simulation results under working condition 3

對于工況1，從圖7（b）和7（c）所示的仿真結果中可以看出，當P小幅階躍但小于P1時，系統穩定。但是P小幅階躍超過P1時，系統失穩。該仿真結果驗證了判據（3）和判據（9）的正確性。

對于工況2，由圖8（b）和8（c）可以看出，當P小于P2時，功率小幅階躍，系統都是穩定的。此外，t=34 s時P階躍到890 W，此時P與P2非常接近，系統等幅振蕩。當t=42 s時，P小幅階躍超過P2，系統振蕩失穩。該仿真結果驗證了判據式（10）的正確性。

對于工況3，由圖9（b）和9（c）中的實線可知，P由8.0 kW階躍到8.7 kW然后再階躍到8.9 kW時，系統穩定。說明P為8.0、8.7和8.9 kW時，系統都是小擾動穩定的。但是，功率P直接由8.0 kW階躍到8.9 kW，如圖虛線所示，系統失穩，因此圖9（b）和9（c）呈現的失穩現象無法通過小擾動穩定分析解釋。然而，通過構建系統平衡點的EDA能夠很好地解釋該失穩現象，為便于下述分析，定義P=8.0、8.7和8.9 kW時，系統的SEP分別為xs1、xs2和xs3。

圖10展示了P=8.7 kW與P=8.9 kW對應的SEP的EDA（Ω2與Ω3）和工況3對應的系統相軌跡。由圖10可見，P=8.0 kW對應的SEP(xs1)在Ω2內、P=8.7 kW對應的SEP(xs2)在Ω3內，因而由李雅普諾夫穩定性定理可知，P由8.0 kW階躍到8.7 kW然后再階躍到8.9 kW對應的暫態過程必然暫態穩定，這與圖9（b）和9（c）的仿真結果一致。此外，由圖10可見，xs1在Ω3外，這說明P直接由8.0 kW階躍到8.9 kW時，系統有可能暫態失穩，這也解釋了圖9（b）和9（c）中P直接由 8.0 kW 階躍到8.9 kW時，系統失穩的原因。

圖10 工況3的機理解釋Fig.10 Mechanism interpretation under working condition 3

4 結 論

本文對含恒功率負載的直流微網系統的穩定性進行了系統性的分析，得到了系統靜態穩定、小擾動穩定的判據和系統SEP的EDA，并通過仿真對理論分析結果進行了驗證，得到以下結論。

（2）系統遭受大擾動時，即使擾動后系統是小擾動穩定的即存在SEP，該暫態過程仍有可能不穩定。只有系統的初始狀態在擾動后系統SEP的吸引域內時，該暫態過程才是穩定的。

綜上，本文得到的靜態穩定、小擾動穩定的判據和系統SEP的EDA對工程應用有一定的借鑒意義。