超高性能混凝土受拉性能試驗研究
方 志,周 騰,劉路明,胡 銳,黃政宇
(1.湖南大學 土木工程學院,湖南 長沙 410082;2.風工程與橋梁工程湖南省重點實驗室,湖南 長沙 410082)
超高性能混凝土(Ultra-high Performance Concrete,UHPC)是一種具有優良力學性能和耐久性的新型水泥基材料,一經出現便引起工程界的矚目[1-2]。UHPC中摻入適量的鋼纖維,可使材料由脆性破壞轉變成延性破壞[3]。因此,鋼纖維是影響UHPC抗拉性能的主要因素。
Hassan等[4]研究了不同齡期UHPC中鋼纖維對其拉伸性能的影響,結果顯示:UHPC中加入2%體積率的鋼纖維后,抗拉強度是基體抗拉強度的近2倍。Park等[5]的研究表明:UHPC中混合纖維體系中微纖維的加入對UHPC的應變硬化和多重開裂性有良好影響。Nguyen等[6]對UHPC軸拉性能的形狀和尺寸效應進行了研究,結果顯示:不同尺寸和幾何形狀UHPC試件的抗拉強度相近,但峰值應變、能量吸收能力和多重開裂現象差別較明顯。楊志慧[7]的研究認為:鋼纖維體積率小于2%的UHPC沒有出現應變硬化現象。杜任遠等[8]測試了UHPC的軸拉強度、抗折強度和劈裂抗拉強度,結果表明:UHPC的三種抗拉強度均隨著鋼纖維摻量的增加而提高。張哲等[9]研究了平直和端鉤混雜纖維對UHPC軸拉性能的影響,結果顯示:混合鋼纖維可提高UHPC材料的可視初裂應變。王俊顏等[10]對UHPC軸拉性能的研究表明:鋼纖維體積摻量為2.5%的UHPC可以達到較高程度的應變強化。
綜上,目前對UHPC軸拉性能方面的研究主要集中在材料的強度和變形方面,但應力-應變關系鮮見包含極限應力處的卸載曲線,導致材料塑性耗能和延性等方面的研究較為缺乏;此外,UHPC軸拉和彎拉、劈拉強度之間的關系需要基于更扎實的數據予以進一步明確。基于此,本文設計制作了15組50個UHPC試件,分別進行了軸拉、彎拉和劈拉測試,以期明確鋼纖維摻量和形狀對UHPC軸拉時耗能和延性的影響以及軸拉、彎拉和劈拉強度間的關系。
1 試驗概況
1.1 原材料及配合比
UHPC基體采用商品干粉料,通過不同鋼纖維的摻入得到所需的UHPC。UHPC的設計強度等級為150 MPa,其配合比見表1,其中硅灰的平均粒徑為89 nm,石英粉的平均粒徑為50.5 μm,石英砂的粒徑范圍為0.55~0.9 mm。鋼纖維分別采用圖1所示的鍍銅平直鋼纖維和端鉤鋼纖維,其基本特征參數見表2。

表1 UHPC基體配合比
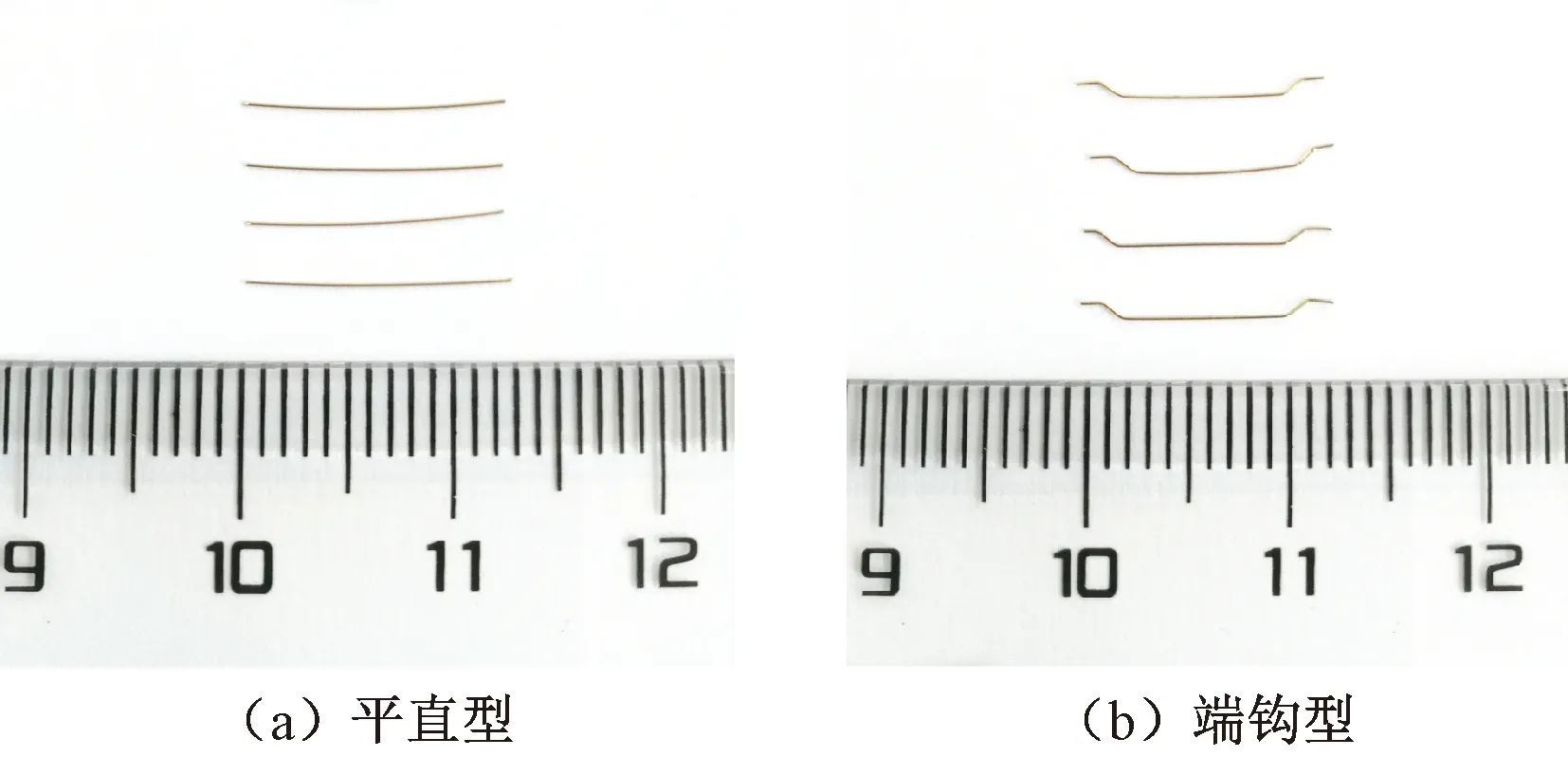
圖1 鋼纖維
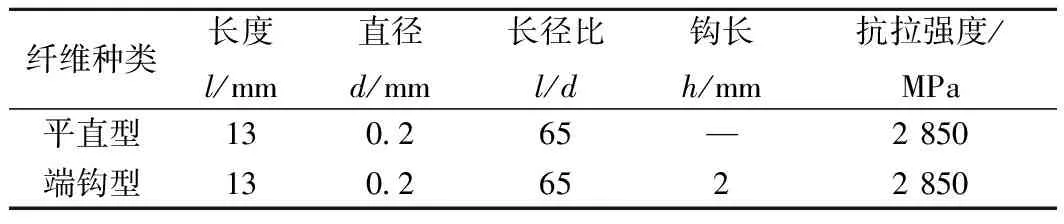
表2 鋼纖維特征參數
1.2 試件設計及制備
迄今為止國內外尚未形成UHPC材料軸拉試驗的統一標準,所用試件的形狀和尺寸不盡相同。試件形狀主要有不開口柱體[11]、開口柱體[12]和狗骨形狀[13]等三類。不開口柱體試件兩端夾持和對中不易且難以保證在標距內破斷;開口柱體試件的截面開口處存在應力集中,難以實現拉伸過程中的多縫開裂現象;狗骨形試件可克服柱體試件的不足[14]。因此,采用圖2所示的狗骨狀試件,測量標距位于中部均勻段,長度為200 mm,截面尺寸為50 mm×30 mm[15]。

圖2 試件形狀尺寸(單位:mm)
彎拉和劈拉強度測試按現行普通混凝土試驗標準進行[16-17],分別采用100 mm×100 mm×400 mm棱柱體和100 mm×100 mm×100 mm立方體試件進行測試。為保證材料性能的一致性,相同纖維摻量的軸拉、彎拉和劈拉試件采用同一盤UHPC澆筑,抗壓性能相同。
以鋼纖維類型(摻量、形狀)和受力特征(軸拉、彎拉和劈拉)為參數,設計制作了15組共50個試件,其中軸拉試件每組4個,彎拉和劈拉試件每組3個,試件參數見表3。
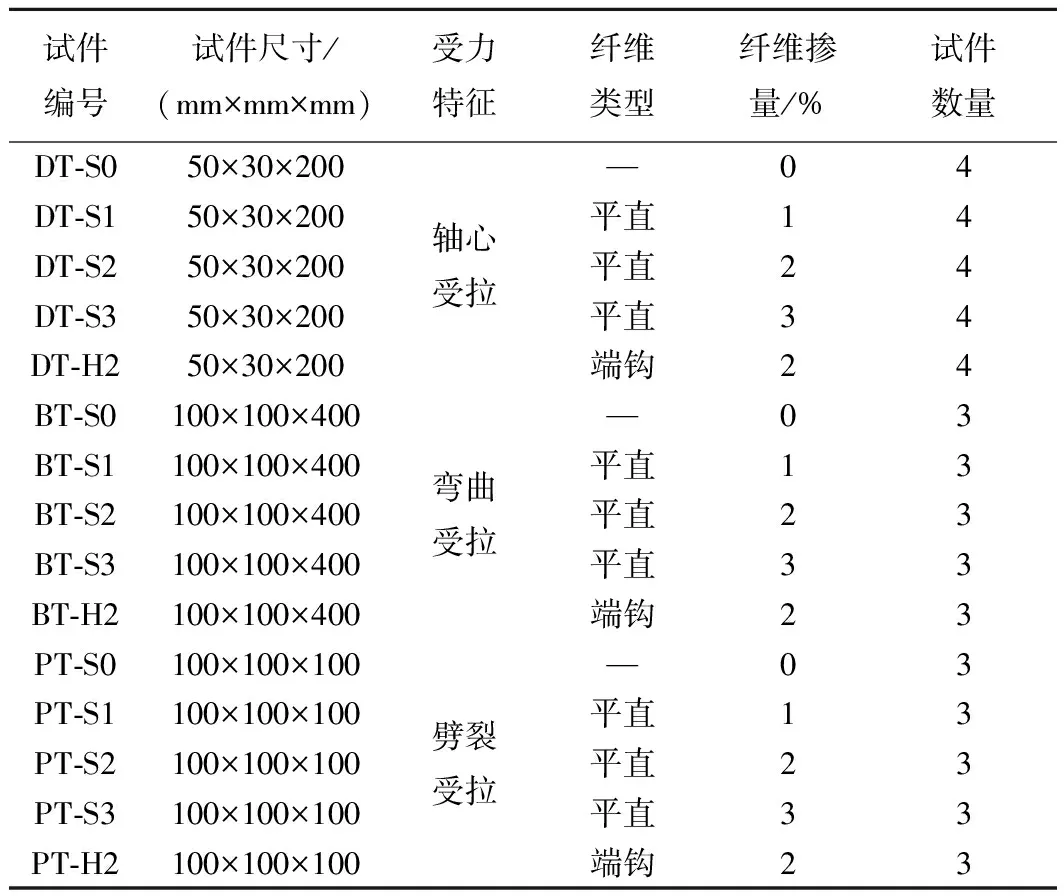
表3 試件參數
所有試件均采用鋼模成型且水平澆筑,為防止振搗對纖維分布的影響,采用自流密實免振搗成型。成型后用薄膜覆蓋表面,常溫下靜置48 h后脫模,然后放入蒸汽養護箱中緩慢升溫至90 ℃,養護72 h后緩慢降至室溫進行試驗[16]。立方體抗壓強度由邊長為100 mm的立方體測得,棱柱體抗壓強度以及受壓彈性模量由100 mm×100 mm×300 mm棱柱體獲得[17-18]。實測材料的基本力學性能見表4,由表4可見:隨鋼纖維摻量的增加,UHPC材料的抗壓強度有所提高,與不摻鋼纖維的基體強度相比,平直鋼纖維摻量為1%、2%和3%時,立方體強度分別增加了5.3%、14.8%和23%,棱柱體強度分別增加了20%、22%和37%;纖維體積摻量為2%時,端鉤纖維試件的立方體強度和棱柱體強度分別較平直纖維試件增加8.6%和1.7%。纖維摻量和形狀對開裂后強度的影響主要是由基體開裂后纖維的橋接和約束作用所致,但其對UHPC彈性模量的影響甚微,這主要是由于彈性模量測試時的上限應力小于基體開裂強度,此時纖維的作用基本尚未發揮。此外,纖維摻量和形狀對UHPC棱柱體與立方體強度比的影響未見明顯規律。
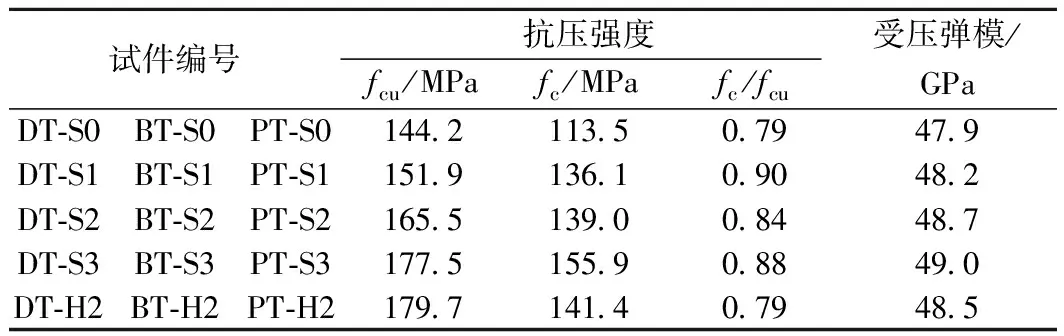
表4 實測UHPC力學性能
1.3 加載方式與測點布置
軸拉試驗在50 kN電子伺服萬能試驗機上進行。試件表面安裝2個高精度位移傳感器,測量200 mm標距內的伸長量,借此獲取測量標距內的平均應變。此外,在試件標距內的兩個表面貼有應變片,以便更準確測量應力-應變曲線的線彈性段和調整試件的對中情況。采用裂縫觀測儀測量試件的裂縫寬度。每組4個試件中,2個試件單調加載至破壞,另外2個試件在荷載降為峰值荷載的85%處進行一次卸載,以期獲得極限狀態時試件的殘余變形和耗能能力,再重復加載至試件斷裂。軸拉試驗的加載速率為0.05 mm/min,卸載速率為0.10 mm/min。
彎拉試驗和劈拉試驗采用普通混凝土的相應標準進行[16-17],加載速率分別取為0.09、0.10 MPa/s。
2 軸拉試驗結果及分析
2.1 破壞形態
軸拉試件出現了單縫脆性破壞和多縫延性破壞兩種模式。
DT-S0和DT-S1試件均發生單縫脆性破壞,且斷口較平直,見圖3(a)、圖3(b)。DT-S0試件開裂后即斷裂,荷載瞬間降為0;DT-S1試件基體開裂后快速發展成一條約0.5 mm的宏觀裂縫,之后荷載快速下降,應變迅速增大,表現出基體開裂后隨變形增加應力降低的應變軟化特征。
DT-S2、DT-S3和DT-H2試件均發生多縫延性破壞且臨界裂縫斷面出現傾斜,見圖3(c)~圖3(e)。基體開裂后受力變形曲線出現拐點,因開裂截面有足夠的鋼纖維予以橋接,使得開裂后變形增長的同時,荷載還有所增長,表現為基體開裂后隨變形增加應力相應增加的應變硬化特征;峰值荷載后,應變增長速度加快,宏觀裂縫穩步擴展,并伴隨鋼纖維被拔出的“滋滋”聲,最終形成一條主裂縫并在此處斷裂。與平直纖維試件DT-S2相比,端鉤纖維試件DT-H2由于端鉤纖維的抗拔能力增強、纖維的拔出速度減緩,使得初裂后的變形平臺加長。

圖3 軸拉試件破壞形態
UHPC是砂漿基體和纖維組成的一種復合材料,其內鋼纖維的摻量決定了基體開裂后材料的受力破壞特征。基體開裂后,由于其內鋼纖維分布的隨機性,使得截面的拉應力分布不再接近均勻,而裂縫總是沿抗拉能力最弱的方向發展,可能導致截面主要裂縫發展方向的變化。當纖維摻量較高時,開裂后鋼纖維的抗拉作用強于基體的抗拉作用,UHPC表現出開裂后的硬化特征,基體開裂后的主裂縫發展方向主要由隨機分布的纖維所決定,因此,主裂縫的發展形態會出現傾斜。當纖維摻量較低(≤1%)時,纖維的抗拉作用弱于基體,UHPC表現出開裂后的軟化特征,且纖維的分布不足以影響基體開裂后的裂縫走向,而UHPC的砂漿基體性能較為均勻,使得軸拉開裂時截面應力分布亦較均勻,因此裂縫開展較為平直。
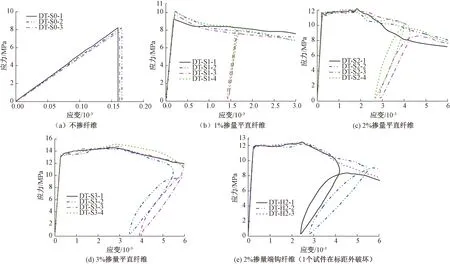
圖4 實測應力-應變關系曲線
2.2 應力-應變曲線特征
定義應力應變曲線初始線性上升段的偏離點為基體開裂點,對應的應力和應變分別為初裂應力(初裂強度)和初裂應變,斜率為抗拉彈性模量;受力變形過程中所經歷的最大應力點稱為峰值應力點(以下簡稱峰值點),對應的應力和應變分別為峰值應力(軸拉強度)和峰值應變。參照目前普通混凝土應力-應變曲線上極限應力點一般取為峰值應力點后應力下降至峰值應力85%處[18]。定義UHPC應力-應變曲線上峰值應力點后應力下降至峰值應力85%處的點作為極限應力點,相應的應力和應變稱為極限應力和極限應變。為明確不同纖維摻入時UHPC的延性和塑性耗能能力,試驗時在極限點處進行卸載,以確定材料卸載后的彈性恢復和殘余的塑性應變,且定義應力從極限點處卸載至0時的點為卸載點,對應的應變為殘余應變,卸載曲線的斜率為卸載模量。
圖4為實測應力-應變全曲線,圖中試件編號后的1~4表示同組試件的序號。由圖4可見:隨著鋼纖維體積摻量的增加,曲線的形狀愈加飽滿并由基體開裂后的軟化逐漸變為強化,且極限點處卸載時的可恢復變形加大、卸載模量降低、殘余變形減小;初始加載、基體開裂、峰值點、極限點和卸載點等特征點間的曲線近似呈線性變化,極限點處卸載后再重新加載時,仍基本能回到卸載前的單調加載曲線運行路徑上。
因此,本文采用圖5所示的多段折線來描述UHPC材料的軸拉應力-應變全曲線。圖5中,σe、εe分別為初裂應力和初裂應變;σp、εp分別為峰值應力和峰值應變;σu、εu分別為極限應力和極限應變;εr為殘余應變;Ec為抗拉彈性模量,Eu為卸載模量;極限點時摻鋼纖維試件吸收的總能量為G+g,其中g為彈性應變能,G為塑性應變能,其值可根據應力-應變曲線下相應部分包圍起來的面積確定。卸載至0后,彈性能完全釋放而塑性能被耗散,塑性能量G反映UHPC的耗能能力。應力均為根據試件初始截面確定的名義應力,應變為測量標距內的平均應變。
基于實測應力-應變曲線得到各試件曲線的特征值見表5。由表5可見:隨鋼纖維體積摻量的提高,UHPC材料的初裂應力和初裂應變稍有增加,峰值應力、峰值應變、極限應變和耗能能力顯著提高。相比于平直纖維,端鉤纖維對初裂強度、初裂應變和峰值應力影響較小,但明顯改善材料的裂后變形能力和耗能能力。這主要是由于纖維的橋接和約束效應僅在基體開裂后才能充分發揮且端鉤纖維的抗拔能力特別是開裂后期的抗拔能力較強。
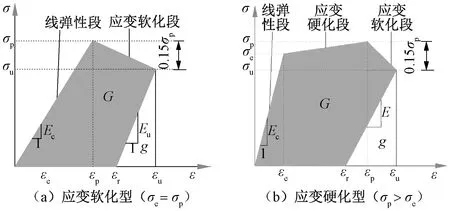
圖5 UHPC典型應力-應變曲線
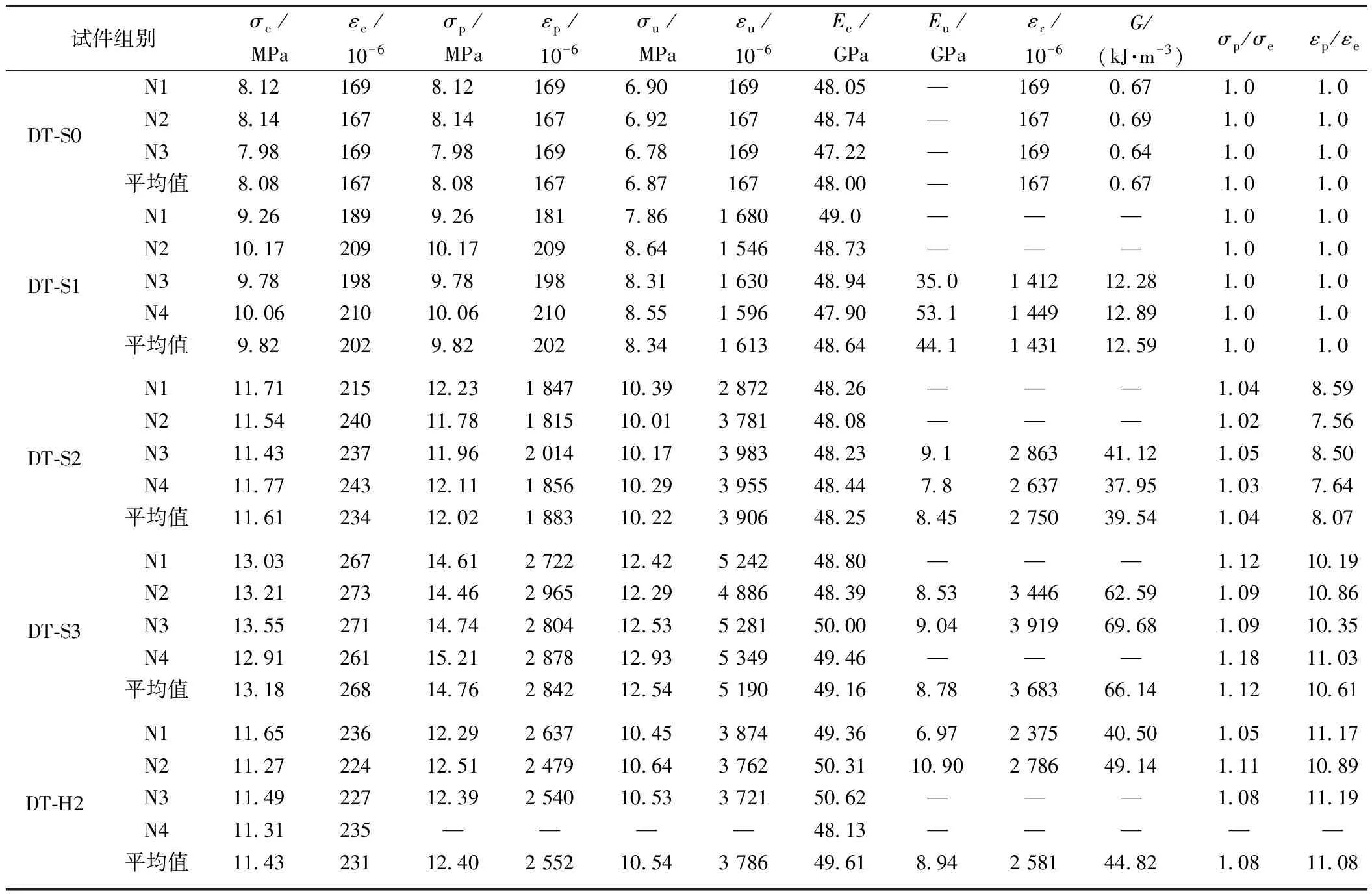
表5 各試件軸拉特征參數
2.3 應力-應變曲線特征參數的影響分析2.3.1 鋼纖維特征參數對曲線彈性階段的影響
試件的基體初裂應力或初裂強度隨鋼纖維特征參數的變化規律如圖6(a)所示。可見:隨鋼纖維摻量的增大,軸拉試件的初裂應力近似呈線性上升趨勢,鋼纖維體積摻量為1%、2%、3%試件的初裂應力分別比無纖維試件增加了21.5%、43.6%、63.1%;相同纖維摻量下,纖維形狀對初裂強度基本上沒有影響。參考文獻[3],確定UHPC的初裂強度σe為
σe=σem(1+ατλf)
(1)
λf=ρflf/df
(2)
式中:σem為基體的抗拉強度;ατ為鋼纖維影響系數;λf為鋼纖維特征參數;ρf、lf、df分別為鋼纖維的體積率、長度、直徑。
基于本文試驗結果,可確定式(1)的鋼纖維影響系數ατ=0.32。
初裂應變隨鋼纖維特征參數的變化規律見圖6(b)。由圖6(b)可見:鋼纖維摻量和形狀對初裂應變的影響規律與初裂應力類似,鋼纖維體積摻量為1%、2%、3%試件的初裂應變分別比無纖維試件提高20.9%、40.1%、60.5%,纖維形狀對初裂應變幾乎無影響。鋼纖維含量對初裂強度和初裂應變的影響是由鋼纖維對基體產生的約束效應所致。基于試驗結果,不同鋼纖維摻量時的開裂應變可計算為
εe=εem(1+0.29λf)
(3)
式中:εe、εem分別為試件初裂應變、基體開裂應變。
由表5可見:鋼纖維體積摻量對抗拉彈性模量影響甚微;相同體積摻量下,端鉤纖維試件的抗拉彈性模量僅比平直纖維試件大2.8%。此外,與表4所列UHPC軸壓彈性模量實測值相比,UHPC軸拉與軸壓彈性模量接近,表明開裂前的彈性受力階段,纖維對基體的加強作用極為有限。
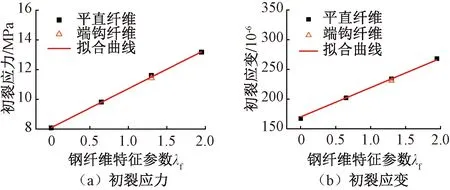
圖6 曲線初裂點參數隨鋼纖維特征參數λf的變化
2.3.2 鋼纖維特征參數對曲線峰值應力點的影響
峰值應力或軸拉強度隨鋼纖維特征參數的變化規律如圖7(a)所示。由圖7(a)可見:鋼纖維體積摻量為1%、2%、3%的試件,其峰值應力分別比無纖維試件提高21.5%、48.7%、82.7%。纖維摻量相同時,端鉤纖維試件DT-H2的峰值應力僅較平直纖維試件DT-S2增大3.2%,影響較小。基體開裂后只有橋接的鋼纖維承受拉應力,纖維摻量相同時,開裂截面上的鋼纖維數量差異不大,故纖維類型對UHPC峰值應力的影響較小。
基于試驗結果,得到峰值應力或軸拉強度的預測式為
σp=σem(1+0.41λf)
(4)
式中σp、σem和λf分別為UHPC的峰值應力、基體抗拉強度和鋼纖維特征參數。
峰值應變隨鋼纖維特征參數的變化規律如圖7(b)所示。由圖7(b)可見:纖維摻量和形狀對峰值應變的影響均較顯著。對于平直纖維,纖維摻量為1%、2%、3%的試件,其峰值應變分別比無纖維試件提高1.21、10.28、16.02倍;同為2%體積摻量下,端鉤纖維試件的峰值應變比平直纖維試件增加了35.5%,這主要是由于端鉤纖維的抗拔能力增強,纖維的拔出速度減緩,拔出前能耐受更大的變形。纖維含量小于1%時,不存在應變硬化特性,初裂點即為峰值點,其峰值應變可按式(3)計算確定;含量不小于1%時,平直鋼纖維UHPC的峰值應變計算式為
εp=αpεem1(-4.2λf2+21λf-10.9)
(5)
式中:εp、αp、εem1分別為試件峰值應變、端鉤纖維增大系數(αp=1.35)、含量1%平直鋼纖維UHPC的峰值應變。
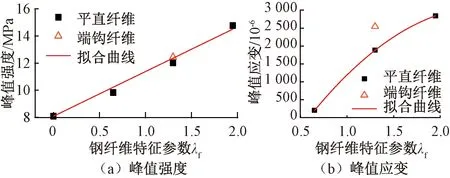
圖7 峰值點參數隨鋼纖維特征參數λf的變化
2.3.3 鋼纖維特征參數對峰值點后曲線的影響
極限應變隨鋼纖維特征參數的變化規律如圖8(a)所示。平直纖維試件的極限應變隨著鋼纖維特征參數變化的規律與峰值應變類似。鋼纖維體積摻量為2%和3%的試件,其極限應變分別比含量為1%的試件增加了142.2%和221.8%。相同體積摻量下,端鉤纖維試件的極限應變略低于平直纖維試件,峰值點后曲線的下降速率稍快于平直纖維試件,這主要是由于端鉤纖維雖然拔出過程較長、峰值點應變增大,但拔出過程中對基體有所損傷、拔出時黏結力消失更快[5]。根據試驗數據擬合得到的極限應變預測公式為
εu=εem1(-5.9λf2+29λf-8.4)
(6)
極限點處的卸載模量隨著鋼纖維特征參數的變化規律如圖8(b)所示。鋼纖維體積摻量為1%、2%、3%試件的卸載模量分別為其初始加載彈性模量的90.7%、17.5%、17.8%,表明當含量不大于2%時,鋼纖維摻量的增加可顯著提升材料的可恢復性能,但當含量大于2%時,鋼纖維摻量對可恢復性能的影響減弱;端鉤纖維試件DT-H2的卸載模量是抗拉彈性模量的18%,與平直纖維試件DT-S2相近,表明纖維形狀對可恢復性能的影響較小。
殘余變形隨著鋼纖維特征參數的變化規律如圖8(c)所示。鋼纖維體積摻量為2%和3%的試件,其殘余變形分別比含量為1%的試件增加了92.2%和157.4%。相同體積摻量下,端鉤纖維試件的殘余應變略低于平直纖維試件。基于試驗結果,不同鋼纖維摻量時的殘余變形的計算式為
εr=εr1(-0.32λf2+2.04λf-0.19)
(7)
式中:εr、εr1分別為試件殘余變形、含量1%平直鋼纖維UHPC的殘余變形。
極限點處的耗能能力隨鋼纖維特征參數的變化規律如圖8(d)所示。鋼纖維體積摻量為2%和3%的試件,其耗能能力分別比含量為1%的試件增加了214%和425%;相同體積摻量下,端鉤纖維試件的耗能能力比平直纖維試件增大13%。由表5的結果可以看到,無纖維試件的耗能能力僅為鋼纖維體積摻量1%~3%試件的1%~5%,可見UHPC軸拉時的耗能能力幾乎全部由鋼纖維的變形且基本上是由鋼纖維不可恢復的黏結滑移提供。
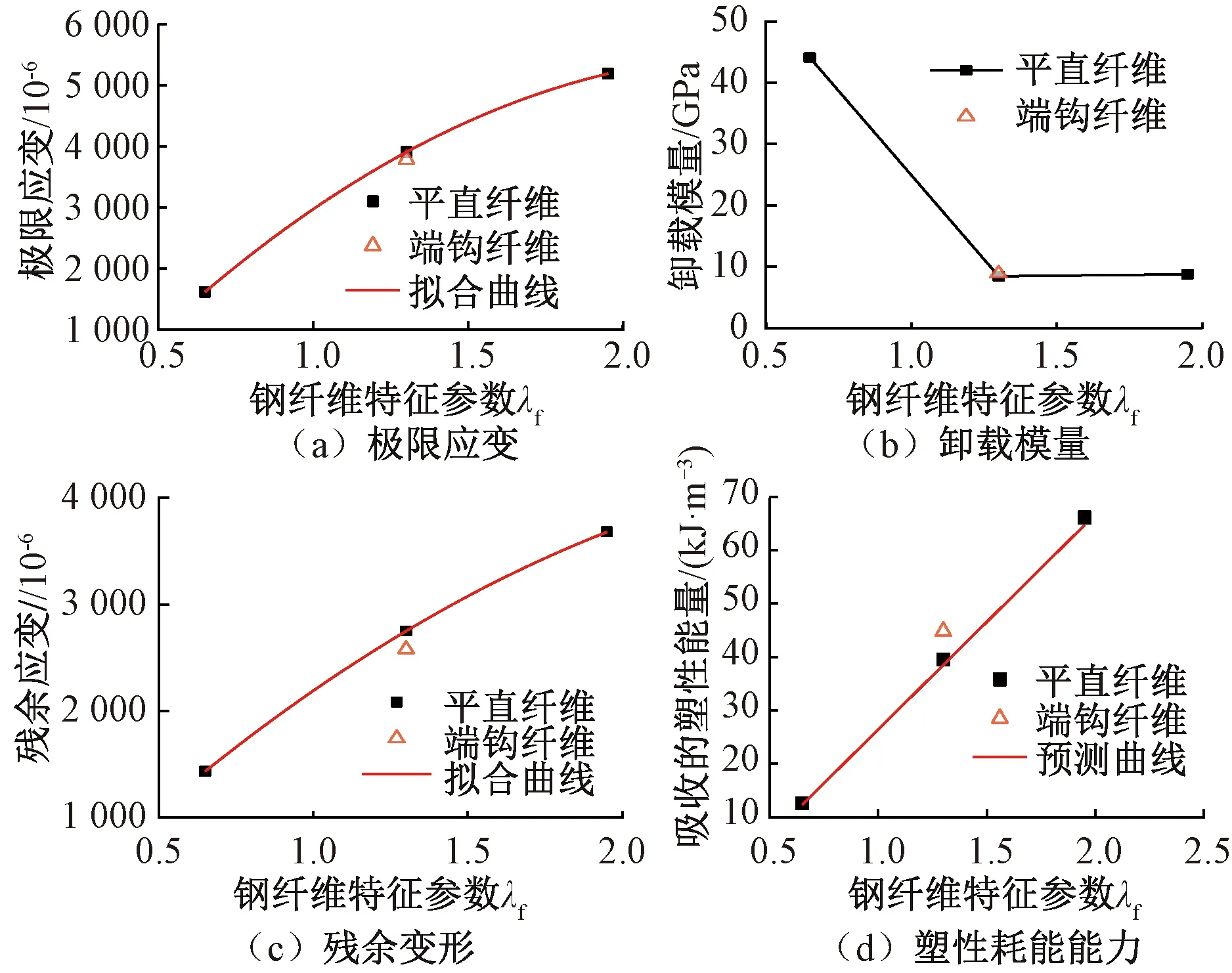
圖8 峰值點后曲線特征隨鋼纖維特征參數λf的變化規律
不同鋼纖維摻量時的耗能能力計算式為
G=αGG1(3.2λf-1.1)
(8)
式中:G、αG、G1分別為耗能能力、端鉤纖維增大系數(αG=1.13)、含量1%平直鋼纖維UHPC的耗能能力。
2.3.4 鋼纖維特征參數對受拉延性的影響
UHPC材料的受拉延性是指其承受的拉應力基本保持不變(最多下降15%)時所具有的塑性變形能力。定義UHPC試件的受拉延性系數[19]為
(9)
式中:μ為延性系數;εe和εu分別為初裂應變和極限應變,可分別按式(3)和式(6)確定。
受拉延性系數隨鋼纖維特征參數的變化規律如圖9所示。鋼纖維體積摻量為2%和3%的試件,其延性系數分別比含量為1%的試件增加了109%和142.5%;相同體積摻量下,端鉤纖維試件的延性系數略低于平直纖維,主要是由于端鉤纖維試件的極限應變略低于平直纖維試件。

圖9 延性系數隨鋼纖維特征參數λf的變化
2.4 鋼纖維特征參數對軸拉裂縫的影響
各纖維加強試件基體開裂后的應力與測量標距內實測最大裂縫寬度的發展曲線如圖10所示。圖10中,各曲線測點為平均值。用測量標距除以標距范圍內的裂縫數量即得到標距范圍內的平均裂縫間距,并與峰值點和極限點處的裂縫寬度一同列于表6。由表6可見:裂縫寬度主要在峰值點后的下降段發展較快;隨著鋼纖維摻量的增加,裂縫數量增多,平均間距降低,但因峰值點和極限點處的應變加大,導致相應的裂縫寬度也更寬。相同體積摻量下,端鉤纖維試件的裂縫間距比平直纖維小27.6%,峰值點和極限點處的裂縫寬度約降低10%,反映了其黏結作用增強導致的裂縫形態變化。

圖10 應力與測量標距內實測最大裂縫寬度的發展曲線

表6 試件裂縫參數
3 軸拉、彎拉和劈拉強度之間的關系
各試件軸拉、彎拉和劈拉強度試驗結果的對比如圖11和表7所示。可見:隨著鋼纖維特征參數的增大,三種抗拉強度均近似線性增加,但彎拉強度fbt增長最快,軸拉強度fdt增長最慢,劈拉強度fpt介于其間,鋼纖維體積摻量為3%時,軸拉、彎拉、劈拉強度分別為相應無纖維試件的1.63、3.06、2.39倍。纖維形狀對三種強度的影響均較小,纖維摻量均為2%時,端鉤纖維試件的軸拉、彎拉和劈拉強度分別為平直纖維試件的0.98、1.09、1.02倍。此外,軸拉強度與彎拉和劈拉強度比均隨鋼纖維特征參數的增大而降低。
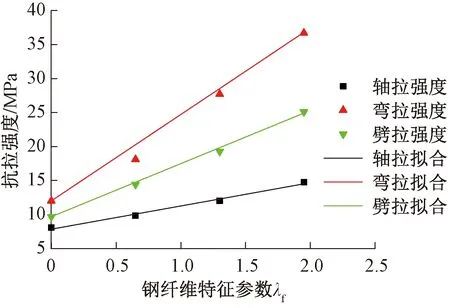
圖11 抗拉強度隨鋼纖維特征參數λf的變化
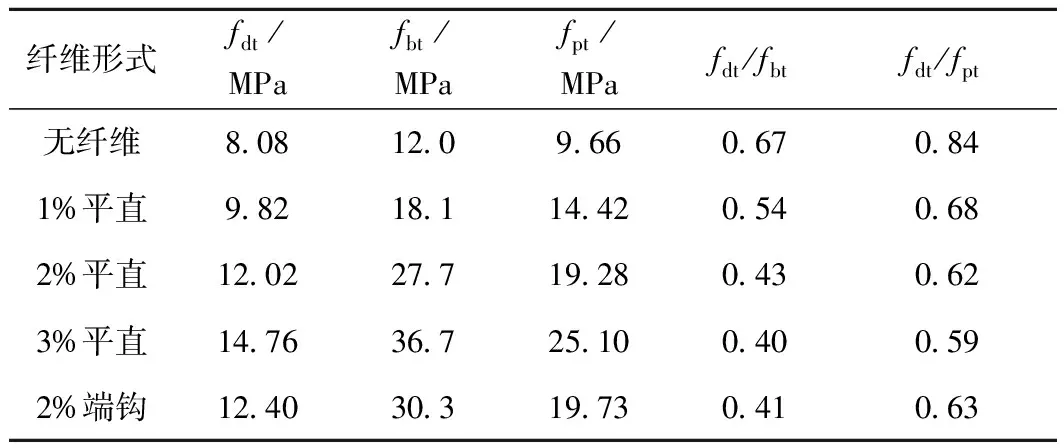
表7 三種不同的抗拉強度對比
UHPC的軸拉強度由式(4)確定,其彎拉和劈拉強度可分別確定為
fbt=fbt0(1+1.06λf)
(10)
fpt=fpt0(1+0.81λf)
(11)
式中:fbt0和fpt0分別為UHPC基體的彎拉和劈拉強度。
基于試驗結果,得到彎拉強度和劈拉強度與軸拉強度之間的統計關系分別為
fdt=(0.06λf2-0.26λf+0.67)fbt
(12)
fdt=(0.08λf2-0.28λf+0.84)fpt
(13)
彎拉強度、劈拉強度與軸拉強度的關系曲線見圖12。需要說明的是,UHPC的強度會存在較明顯的尺寸效應,而本文軸拉與彎拉和劈拉試件的截面尺寸相差較大,這里給出的三種強度間的關系僅依據本文試驗結果總結得出,試件尺寸的影響有待進一步研究。
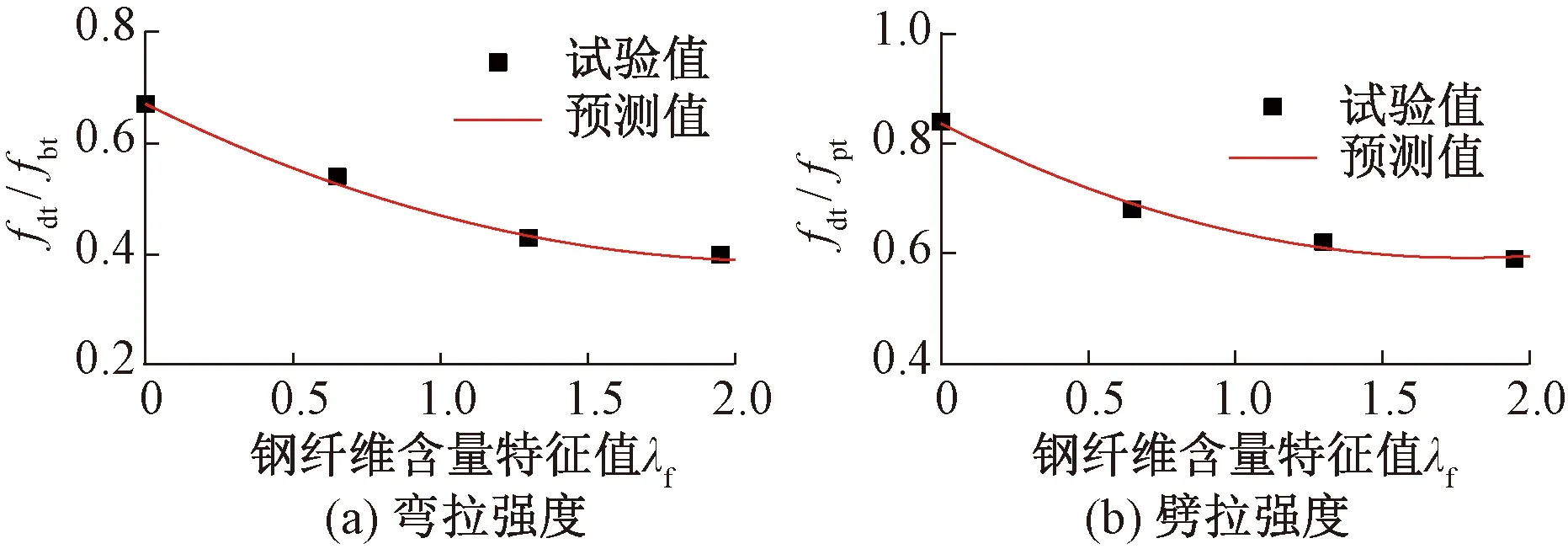
圖12 彎拉強度、劈拉強度與軸拉強度的關系曲線
4 結論
(1)鋼纖維體積摻量為1%時,UHPC軸拉表現出單縫開裂的應變軟化特征,鋼纖維摻量不小于2%時,則表現出多縫開裂的應變硬化特征。
(2)包括卸載曲線在內的UHPC軸拉應力-應變全曲線在初裂點、峰值點、極限點和卸載點等相鄰特征點間基本呈線性變化,基于試驗結果確定了曲線各特征點的取值。受拉與受壓彈性模量相近,材料的塑性耗能能力基本上是由基體內纖維的塑性變形提供。
(3)端鉤纖維僅對UHPC軸拉時的峰值點應變、塑性耗能能力及多縫開裂時的裂縫間距影響較為顯著,對其它性能的影響較小。
(4)隨鋼纖維摻量的增加,UHPC軸拉、彎拉和劈拉強度均近似線性增大且彎拉強度對其最為敏感,軸拉強度與彎拉和劈拉強度比逐漸降低。

