小學數學結構化教學探析

郭葛晨晨

[摘? 要] 小學數學結構化教學中，教師應重視結構關聯，要求學生不僅要關注數學知識點的結構關聯，更要從數學思維和認知層面深入結構關聯，從而促進學生深度學習，實現學生核心素養的關聯生長。

[關鍵詞] 小學數學;結構化教學;運算定律

隨著現代教學實踐中工具的使用越來越頻繁，學生在學習過程中的信息獲取也越來越碎片化。隨之影響的是學生的思維習慣和認知深度，學生的思維和認知缺乏整體性和關聯性，難以搭建起統一的結構主體。小學數學結構化學習是指基于數學知識，將數學知識結構化，形成知識體系，幫助學生深刻理解數學知識和發展數學思維。基于此，開展小學數學結構化教學，不僅要求教師關注數學知識的結構關聯，還要從學生認知和思維層面深入探究實踐思路。通過不斷探索、有效整合、及時反思，幫助學生經歷認知形成和思維重塑的過程，從而建構起學習數學知識的基本思路，為后續的數學深度學習打下堅實基礎。

一、探析數學知識點的結構關聯

要如何理解“幫助學生搭建知識點的結構關聯，有助于學生深刻理解知識，并靈活運用知識”這一結論呢？我們可以從美國著名認知心理學家布魯納說過的一句話中找到答案，即“掌握事物的結構，就是以使許多別的東西與它有意義地聯系起來的方式去理解它”。具體來說，要想完成小學數學的結構化教學，我們必須從數學知識點出發，通過探究數學知識的結構關聯，幫助學生搭建數學知識的完整框架。要想抓住數學知識的本質，我們可以依據教材，從課時內容的各個關鍵環節出發，探究它們之間的關聯性，再分析課時內容與同單元其他章節內容、同板塊其他單元內容、同學科其他板塊內容之間的關聯性，幫助學生從內到外深度理解知識，從外到內循環高效發展思維。

1. 關聯分析課時內容的關鍵部分

從數學知識的本質出發，通過分析課時內容的關鍵部分完成對知識的分析和建構，從而不斷優化教學內容和呈現思路，豐富教學品質，提升教學質量。

【案例】 以“運算定律”這一章節的教學為例，我們可以將這部分內容，拆解成加法定律和乘法定律這兩個大的課時，進而分解為加法交換律、加法結合律、加法運算定律的應用、簡便運算，乘法交換律、乘法結合律、乘法分配律，復雜問題的多樣運算。通過對這些關鍵知識再排列和再認知，實現數學學習的再創造，從而不斷提升學習效果和教學品質。

2. 關聯分析課時內容與同單元其他章節內容

課時內容并不是單一孤立存在的，它們是有聯系的，相互的聯系構成了一個有機整體。因此，教師在完成對課時內容的講授后，要關注同單元其他章節內容與本課時內容的聯系，幫助學生認識課時內容與其他章節內容之間的結構關聯，發現它們之間的內在聯系，做好互相滲透、銜接、過渡，從而完善學生的認知結構。

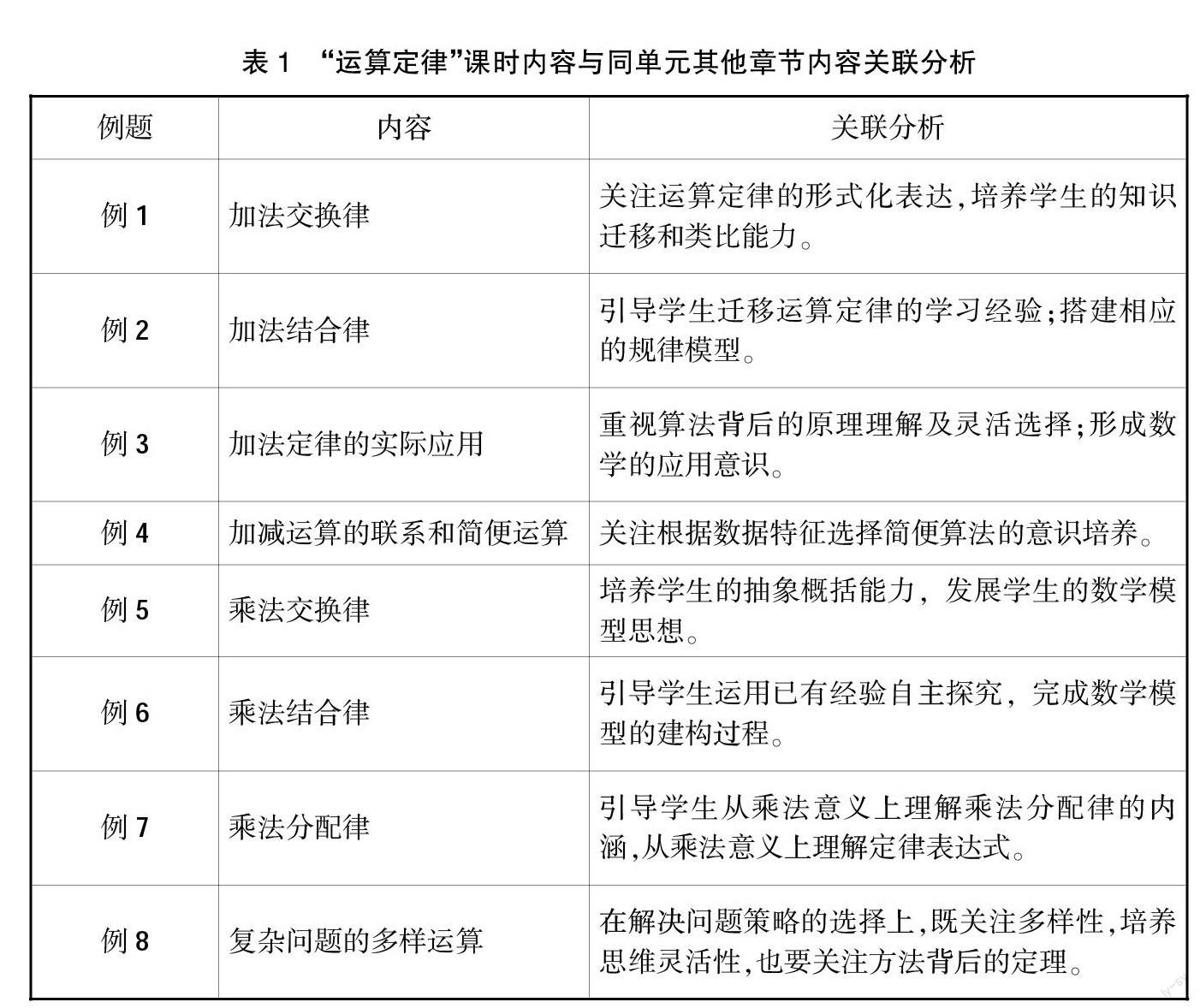
【案例】 以“運算定律”這一章節的教學為例，我們基于教材例題對本章節課時內容與同單元其他章節內容進行對比分析，如表1所示。

從表1中我們可以看出，本課時內容“運算定律”是整個單元的重點，在章節學習中起著重要作用。在這一課時中，學生必須直觀并且深刻地了解和認識加法與乘法的運算定律，并將它們延伸至減法和除法，學生需要學會計算復雜問題，并能應用定律解決實際問題。

3. 關聯分析課時內容與相關單元內容

如果將課時內容比作一個點，那么單元內容是一條線，相關單元內容即是一個面，由點及線，由線到面，形成知識體系。因此，教師在實際教學活動中，要充分認識課時內容在相關單元內容中的重要性，明確板塊教學的要求，努力構建點線面全面覆蓋的整體認知結構。

【案例】以“運算定律”這一內容為例，這一課時內容是四則運算的重點，教師除了要聯系之前教學實踐中總結的經驗和規律，幫助學生理解加法或乘法交換律（交換兩個加數或因數的位置，不改變計算結果），還要聯系后續的小數加減法和乘除法混合運算，幫助學生搭建起有關實數的四則運算的整體知識框架。

二、探析數學認知的結構關聯

數學知識是學生在解決數學問題的過程中獲得并內化的。在這個過程中，學生依序建構活動程序和對象，最終組織概括成可以理解問題、解決問題的整體架構。學生的數學學習一般要經歷以下四個認知階段：

1. 活動階段

活動包括具體的外在的動作，例如實驗、操作、游戲等，還包括內在的思維活動，如回憶、對比、猜想等。它是幫助學生一步步加深對數學對象的認識印象的有效途徑。在實際的教學實踐中，教師應當給予符合學生思維的問題情境，引導學生通過相應的活動初步感知數學對象。

2. 程序階段

當活動經過多次重復而被學生熟悉和認識后，就可以內化為一種被稱為程序的心理反應。學生具備這種程序后，就能在頭腦中自動化運行而不需要具體操作。經過多次重復的反思后，學生可以逐步剔除數學對象的非本質屬性，從而認識數學對象的本質屬性。

3. 對象階段

當學生能將程序作為一個整體進行獨立操作和概括總結時，這個程序就變成了一種心理對象，可以幫助學生實現從感性認識到理性認識的飛躍，從而發生質變。通過活動和程序認識，學生可以抽象概括出數學對象的本質屬性，從而將其變得形式化或符號化，成為一個可以參與到結構關聯中的獨立個體。這樣學生就可以將其作為一個數學認知帶入新的數學活動中，提升數學活動的思維層次，如此往復，學生的數學認知水平將會不斷提高。

4. 圖式階段

當學生對活動程序和對象進行有機整合并形成初步的認知結構時，圖示應運而生。這個階段是學生認知的結構化階段，通過圖示可實現數學學習關聯結構化。當然，學生的初步圖示不可能盡善盡美，還需要在后續的學習和解題實踐中不斷修正與完善，因此教師在后續的數學教學過程中，要引導學生不斷更新和反思認知結構，幫助學生豐富圖示的內涵和本質。在具體教學實踐中，教師可以通過思維導圖、韋恩圖、知識結構框架圖等讓學生學會梳理數學知識，幫助學生總結歸納數學知識，提升學生的建構能力和認知水平。

三、探析數學思維的結構關聯

數學思維是數學認知的核心，構建認知結構的目的就是幫助學生發展數學思維，提高解題的靈活性。在小學數學結構化學習過程中，學生的思維發展主要有直觀思維、程序思維、抽象思維和形式思維等階段。教師在實際教學活動中要把握住學生思維發展和認知發展是一一對應的。也就是說，隨著學生知識結構的逐步完善，數學認知水平的不斷深入，其數學思維也會不斷成長，因此，只要做好學生知識點的結構關聯和認知水平的基礎搭建，學生的數學思維能力就一定會有較大提升。

當然，小學數學的結構化教學，并不僅僅局限于數學知識點的結構關聯、數學認知的結構關聯和數學思維的結構關聯，還包括數學情感和價值觀的建立、數學方法的學習。鑒于文章篇幅有限，這里就不一一詳述，大家可以根據實際教學經驗自行探究分析。