透視“最短路徑”，探索思路突破

王律奇

[摘? 要] “螞蟻爬行最短路徑”是中考的常考題型，問題將三視圖與空間幾何相結(jié)合，考查空間轉(zhuǎn)化和實(shí)際應(yīng)用. “兩點(diǎn)之間，線段最短”是破題的核心定理，解題時(shí)需要在展開圖形中構(gòu)建直角三角形，利用勾股定理來求線段長(zhǎng). 文章結(jié)合2021年南京市的中考?jí)狠S題，開展解題探究，并進(jìn)一步總結(jié)拓展.

[關(guān)鍵詞] 幾何;最短路徑;展開;旋轉(zhuǎn)體

“螞蟻爬行最短路徑”在中考中時(shí)有出現(xiàn)，該類問題將幾何體與平面圖形有機(jī)結(jié)合，實(shí)現(xiàn)了簡(jiǎn)單的空間轉(zhuǎn)化，可考查三視圖、平面幾何相關(guān)知識(shí)以及思維轉(zhuǎn)化能力，下面進(jìn)行具體探究.

考題呈現(xiàn)，背景揭示

1. 考題呈現(xiàn)

考題? （2021年江蘇省南京市中考數(shù)學(xué)卷第27題）在幾何體表面上，螞蟻怎樣爬行路徑最短？

（1）如圖1所示，圓錐的母線長(zhǎng)為12 cm，B為母線OC的中點(diǎn)，點(diǎn)A在底面圓周上，的長(zhǎng)為4π cm. 在圖2所示的圓錐的側(cè)面展開圖中畫出螞蟻從點(diǎn)A爬行到點(diǎn)B的最短路徑，并標(biāo)出它的長(zhǎng)（結(jié)果保留根號(hào)）.

（2）如圖3所示，該幾何體由底面半徑相同的圓錐和圓柱組成. O是圓錐的頂點(diǎn)，點(diǎn)A在圓柱的底面圓周上. 設(shè)圓錐的母線長(zhǎng)為l，圓柱的高為h.

①螞蟻從點(diǎn)A爬行到點(diǎn)O的最短路徑的長(zhǎng)為________（用含l，h的代數(shù)式表示）.

②設(shè)的長(zhǎng)為a，點(diǎn)B在母線OC上，OB=b. 圓柱的側(cè)面展開圖如圖4所示，在圖中畫出螞蟻從點(diǎn)A爬行到點(diǎn)B的最短路徑的示意圖，并寫出求最短路徑的長(zhǎng)的思路.

2. 背景揭示

本題目中螞蟻從幾何體的某一點(diǎn)出發(fā)，沿著表面爬行到另一點(diǎn)，求最短路徑，屬于典型的“幾何體表面線段最值”問題. 問題突破需要學(xué)生具備較強(qiáng)的空間想象能力，以及良好的學(xué)科素養(yǎng). 對(duì)于螞蟻在幾何體表面爬行問題，學(xué)生解析時(shí)通常需將幾何體展開成平面，然后運(yùn)用勾股定理來計(jì)算最短路程，即利用“化曲為平”“化折為直”的思想來解決.

需要注意的是，幾何平面展開的方式有多種，不同方式可形成不同的爬行路徑，故需要理性思考、操作實(shí)踐、分類總結(jié)，才可以確定方案，形成策略. 同時(shí)要注重?cái)?shù)形結(jié)合的解題思想，深刻理解“兩點(diǎn)之間，線段最短”原理的內(nèi)涵.

考題分析，思路突破

上述探究幾何體表面螞蟻爬行中的最短路徑，最顯著的特點(diǎn)是涉及了圓錐體，其表面展開為扇形，必然含有圓弧，問題解析需要學(xué)生掌握?qǐng)A弧的相關(guān)知識(shí)，下面進(jìn)行具體探究.

1. 初探第（1）問

該問中的幾何體為單圓錐，題干中直接呈現(xiàn)了圓錐展開的平面圖——扇形，需要構(gòu)建幾何體與平面之間的關(guān)聯(lián).

求由點(diǎn)A爬行到點(diǎn)B的距離，根據(jù)“兩點(diǎn)之間，線段最短”可知在平面圖中就為線段AB的長(zhǎng).

連接OA，AC，如圖5所示. 設(shè)∠AOC=n°，由于圓錐的母線長(zhǎng)為12 cm，的長(zhǎng)為4π cm，由弧長(zhǎng)公式可得=4π，解得n=60. 因?yàn)镺A=OC=12，所以△OAC為等邊三角形. B是母線OC上的中點(diǎn)，由“三線合一”可知AB⊥OC. 在Rt△ABO中，AB=OA·sin60°=6.

評(píng)析? 上述題設(shè)較為簡(jiǎn)單，只需建立幾何體表面與平面圖形之間的關(guān)聯(lián)，利用對(duì)應(yīng)定理即可確定最短距離. 本質(zhì)上為簡(jiǎn)單的平面幾何問題，突破的關(guān)鍵是分析△ACO的特性.

2. 深探第（2）問

該問設(shè)定幾何體為圓錐和圓柱的組合，需要注意兩點(diǎn)：一是兩幾何體展開后的平面圖形，即圓錐展開為扇形，而圓柱展開為長(zhǎng)方形;二是平面圖形之間的關(guān)聯(lián)，扇形的圓弧長(zhǎng)=長(zhǎng)方形的一邊長(zhǎng). 探究幾何體表面兩點(diǎn)之間的距離，體現(xiàn)在平面中即為兩點(diǎn)之間的距離.

①該問求點(diǎn)A到點(diǎn)O的最短距離，其中A為圓柱體底面圓周上一點(diǎn)，O為圓錐的頂點(diǎn)，觀察可知最短路徑為：先沿著過點(diǎn)A且垂足于底面的直線爬行到圓柱上底面圓周上，再沿著圓錐母線爬行到頂點(diǎn)O上，顯然最短路徑長(zhǎng)就為母線長(zhǎng)l加上圓柱的高h(yuǎn)，即l+h.

②該問求點(diǎn)A到點(diǎn)B的最短距離，其中點(diǎn)B在母線OC上，需要畫出點(diǎn)A到點(diǎn)B的最短路徑，體現(xiàn)在平面中只需連接AB即可. 該問的特點(diǎn)是不需要求AB長(zhǎng)，但需寫出相應(yīng)的解題思路，思路需要體現(xiàn)兩點(diǎn)：一是求解點(diǎn)、線的順序;二是呈現(xiàn)求點(diǎn)、線的具體模型、定理、公式.

求最短路徑長(zhǎng)的思路如下：如圖6所示，連接OG，過點(diǎn)G作AD的垂線OF，垂足為F，由題意可知OG=OC=l，GF=C′D=h，OB=b. 求解順序如下：

①由于的長(zhǎng)為a，則展開后線段AD=a，可設(shè)線段C′G=x，則弧長(zhǎng)=x，結(jié)合母線長(zhǎng)l可求出∠COG.

②再過點(diǎn)B作OG的垂線BE，垂足為E. 因?yàn)镺B=b，在Rt△OEB中使用三角函數(shù)，可求出OE和BE的長(zhǎng)，從而可得到GE的長(zhǎng)，利用勾股定理即可表示出BG的長(zhǎng).

③由于FD=C′G=x，則可得AF=a-x，在Rt△AGF中，用勾股定理可表示AG. 由AF+FH可得AH，由EG+GF可得HB.

④由于“兩點(diǎn)之間，線段最短”，故需要求A，G，B三點(diǎn)共線，在Rt△ABH中，由勾股定理可得AB2=AH2+BH2，代入線段長(zhǎng)可構(gòu)建關(guān)于x的方程，即可求得x的值.

⑤再將x的值回代到BG和AG中，求其和即可得到最短路徑長(zhǎng).

評(píng)析? 上述第（2）問同樣是求幾何體表面兩點(diǎn)之間的距離，其特殊之處在于兩點(diǎn)位置一般，需要學(xué)生在展開的平面中構(gòu)建模型. 其中第（2）問更為新穎，利用圓柱和圓錐構(gòu)建了組合體，側(cè)面展開圖則為扇形和長(zhǎng)方形的組合. 問題解析全方位呈現(xiàn)了思路構(gòu)建的過程，對(duì)學(xué)生的思維有著較高的要求，雖簡(jiǎn)略了解題過程，但考查思路更具挑戰(zhàn)性.

解后總結(jié)，拓展關(guān)聯(lián)

1. 解后總結(jié)

“螞蟻爬行問題”屬于幾何情景問題，將立體幾何與平面幾何充分結(jié)合起來，問題考查三大方面：一是立體幾何與三視圖;二是幾何的知識(shí)定理;三是數(shù)學(xué)幾何在實(shí)際中的應(yīng)用. “兩點(diǎn)之間，線段最短”是破解“最短路徑”問題的核心定理. 基于幾何體，可將問題分為兩大類型：一是旋轉(zhuǎn)體，如上述所涉及的圓錐、圓柱，此外還有球體等;二是非旋轉(zhuǎn)體，如常見的棱柱、棱錐. 問題解析需要學(xué)生關(guān)注不同類型幾何體的展開圖，掌握對(duì)應(yīng)的三視圖.

類型一：旋轉(zhuǎn)體，需要重點(diǎn)掌握?qǐng)A錐和圓柱的展開圖，圓錐的側(cè)面展開圖為扇形，幾何體與展開圖的關(guān)聯(lián)如下：①圓錐體的母線→扇形的半徑;②圓錐體底面周長(zhǎng)→扇形圓弧長(zhǎng). 而圓柱的展開圖為長(zhǎng)方形，幾何體與展開圖的關(guān)聯(lián)如下：①圓柱的高→長(zhǎng)方形的寬;②圓柱的底面周長(zhǎng)→長(zhǎng)方形的長(zhǎng).

類型二：非旋轉(zhuǎn)體，需要重點(diǎn)掌握棱柱和棱錐，兩者展開均為幾何常見的圖形，對(duì)于規(guī)則的棱柱則為長(zhǎng)方形，可直接利用平面幾何知識(shí)分析;對(duì)于一般的棱錐，則可以考慮直接沿著一條側(cè)棱展開，則展開圖為三角形的串聯(lián)組合，連接相關(guān)點(diǎn)，構(gòu)建三角形即可求解最短線段.

2. 拓展關(guān)聯(lián)

考題屬于“螞蟻爬行問題”中的類型一——旋轉(zhuǎn)體，下面結(jié)合一道例題進(jìn)一步探究類型二——非旋轉(zhuǎn)體的突破過程.

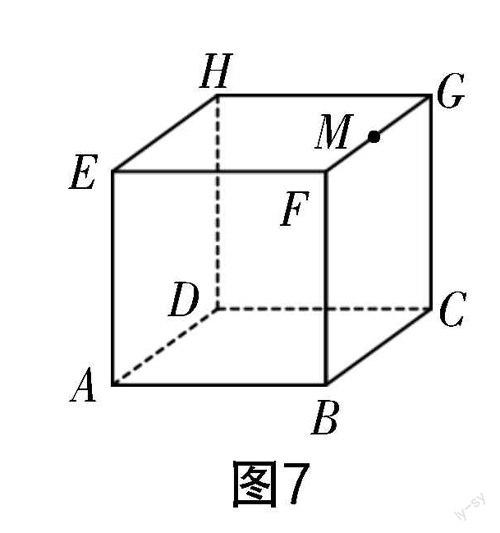
例如圖7所示，正方體的棱長(zhǎng)為2，一只螞蟻在頂點(diǎn)A處，在頂點(diǎn)G處有一粒米.

（1）若螞蟻要吃到這粒米，需要爬行的最短距離為多少？

（2）若螞蟻剛準(zhǔn)備出發(fā)時(shí)，突然一陣風(fēng)將米粒吹到了GF的中點(diǎn)M處，螞蟻要想吃到該粒米需要爬行的最短距離為多少？

分析：正方體的側(cè)面展開圖為長(zhǎng)方形，在長(zhǎng)方形中連接相關(guān)點(diǎn)，構(gòu)建直角三角形，利用勾股定理求解即可.

（1）該情形長(zhǎng)方體的側(cè)面展開圖如圖8所示，連接AG，則AG的長(zhǎng)就為最短路徑. 因?yàn)檎襟w的棱長(zhǎng)為2，所以AC=4，CG=2，在Rt△ACG中，由勾股定理可得AG==2，即螞蟻要吃到這粒米，需要爬行的最短距離為2.

（2）米粒位于點(diǎn)M處，而M為FG的中點(diǎn)，則側(cè)面展開圖如圖9所示.

由題意可知AN=AB+BN=3，MN=2，在Rt△AMN中，由勾股定理可得AM==，即螞蟻要吃到這粒米，需要爬行的最短距離為.

評(píng)析? 上述考題以正方體為背景，“線段最短”與“勾股定理”組合是問題的根本所在，掌握其側(cè)面展開圖是解題的關(guān)鍵. 對(duì)于幾何體中的點(diǎn)，學(xué)生解題時(shí)需要將其定位到展開圖中，依托幾何圖形的性質(zhì)來研究線段長(zhǎng).

寫在最后

“螞蟻爬行最短路徑”問題在中考中十分常見，可全面考查學(xué)生的空間幾何觀以及幾何分析轉(zhuǎn)化能力. 將幾何體展開是解題的首選方法，可實(shí)現(xiàn)問題的平面化，問題解析要關(guān)注其中的特殊位置，以其為紐帶構(gòu)建模型.

該類問題較為新穎，源于教材，又高于教材，問題中蘊(yùn)含了豐富的幾何知識(shí)和數(shù)學(xué)思想. 教學(xué)中教師要指導(dǎo)學(xué)生掌握解題的核心定理，合理滲透數(shù)學(xué)的化歸轉(zhuǎn)化、模型思想等，引導(dǎo)學(xué)生體驗(yàn)解題過程，體會(huì)思路構(gòu)建，提升學(xué)生的解題思維，培養(yǎng)學(xué)生的空間幾何觀.