對一道解三角形題的解法探究

1 試題再現

如 圖 1，在 △ABC中，AB⊥BC，AD=DE，∠DAE=∠ACB，BD=1.（Ⅰ）求CE的長；（Ⅱ）若E為CD的中點，求cos ∠EAC.

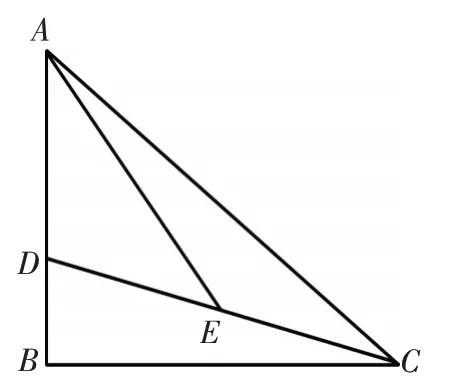
圖1

分析:（Ⅰ）設∠ACB=α(0 ＜α＜),依據題意得到BC=tan 2α，CD=，進一步得到AB,AD，然 后 得 到CE=-tanαtan 2α+1，進行化簡即可.

（Ⅱ）根據（Ⅰ）可得DE，cosα=，進一步得到AE,AC，然后使用余弦定理計算即可.

2 試題解析

（Ⅰ）解法1：設∠ACB=α，則∠DEA=∠DAE=α，∠CDB=2α，又AB⊥BC，BD=1 ，故BC=tan 2α，CD=，AB=BCtanα=tanαtan 2α，AD=AB-1=tanαtan 2α-1，所以CE=CD-DE=CD-AD

評析：本題第一問充分利用了直角三角形中三角函數的定義，利用角表示了三角形中的各條邊，從而將求線段長度的問題轉化為三角函數式的化簡問題，解法獨特，下面針對第一問再給出不同的兩種求解方法.

解法3：（三角形的外接圓）如圖2，以AC為直徑作Rt△ABC的外接圓O，延長AE交圓O于點F，連接FB、FC，過F作FG//AB交DC于G，則∠AFB=∠ACB.因為AD=DE，所 以∠DAE=∠DEA，又因為∠DAE=∠ACB，所以∠AED=∠AFB，所以DG//BF，四邊形BDGF是平行四邊形，所以FG=BD=1，∠DAE=∠GFE，又∠AED= ∠FEG，所以∠GEF=∠GFE，所以GE=GF=1，又EC是Rt△EFC的斜邊，所以G為EC的中點，EC=2GF=2.

圖2