依托旋轉求變式 強化理解提素養

甘肅隴南市禮縣馬河鄉吳宋學校 翟耀輝 742224

旋轉作為圖形的變化方式之一，在初中數學中有重要的應用.它讓原本靜態的數學圖形有了動態感，讓學生從運動的角度來認識圖形的性質與規律，從而讓初中平面幾何的學習更具有內涵與魅力.

1 認識旋轉，強化概念

1.1 旋轉的概念

旋轉就是將一個幾何圖形圍繞著某一個點轉動一定的角度，稱為圖形的旋轉，這個點稱為旋轉中心.在旋轉的過程中轉過的角度稱為旋轉角，圖形上的點在旋轉轉動下到達另一個點，則稱此兩點為對應點.

從旋轉的概念我們不難體會到，把握好旋轉過程的對應點，認準旋轉產生的角，是認識旋轉圖形，理解旋轉概念的的關鍵.

1.2 旋轉的性質

從旋轉的概念我們發現，圖形中的對應點與旋轉中心的距離是等量的，旋轉后形成的圖形與旋轉前的圖形能夠完全重合，因而它們全等.從旋轉來理解圖形的性質，避免了單調而生硬的證明，讓學生的學習更加輕松易懂.

2 運用旋轉，尋求變式

例1 如圖1，正方形ABCD，點E在邊CD上，繞點A把△ADE順時針旋轉90°，得到△ABF，將EF連接，EF垂直AG，如 果BG=3 ，CG=2 ，求CE的長為多少？

圖1

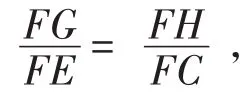
本題以正方形為背景，通過旋轉設置問題情境，考查學生對數學知識的掌握與運用.正方形是初中平面幾何中最為重要的圖形之一，它融矩形與菱形為一體，內涵豐富，性質多樣，同時又可以看作是兩個全等的直角三角形拼接而成，因而在以正方形為背景的問題解決中，其運算就可以借助勾股定理而成為解題的突破口.

例2 如圖2,正方形ABCD，AB=6,∠EAF=45°，AE與BC相交于E點，AF與CD相交于F點，連接EF，把△ADF順時針繞點A旋轉90°到△ABG的位置.如果DF=3，求BE的長是多少？

圖2

本題可以看作是例1 的變式，其基本圖形與例1 相似，但是“萬變不離其宗”，勾股定理的運用完成了本題的求解.

例3 如圖3，正方形ABCD的邊上兩點M，N，當∠MAN=45°時.將△ADN順時針繞點A旋轉90°后，到達△ABE的位置.（1）求證：△AEM≌△ANM.（2）如果BM= 3 ，DN=2 ，那 么 正 方 形ABCD的邊長為多少？

圖3

分析與解答（1）證明：因為△ADN≌△ADE，所以∠DAN=∠BAE，DN=BE，又因 為∠DAB=90°，∠MAN= 45°，所 以∠MAE=∠BAE+∠BAM=∠DAN+∠BAM=45°，于是∠MAN=∠MAE，得到△AEM≌△ANM.

（2）解：令CD=BC=x，則CM=x-3 ，CN=x-2，因為△AEM≌△ANM，所以EM=MN，又因為BE=DN，所以MN=BM+DN=5，同時∠C=90°，故MN2=CM2+CN2，所以(x-2)2+(x-3)2=25 ，解得x=6 或x=-1（舍棄），即正方形ABCD的邊長為6.

本題利用了例1及其變式例2的基本圖形，通過增加設問的方式，滲透了學生對正方形與旋轉性質的運用，較之前兩道題目，難度稍大，運算量稍多，體現了對學生數學核心素養之運算能力的考查.

例4 如圖4，點E在正方形ABCD的內部，當∠AEB=90°時，把直角△ABE沿著順時針方向繞點B 旋轉90°，到達△CBE′的位置.延長線段AE與線段CE′交于F點并連接線段DE.（1）請判斷四邊形BE′FE的形 狀，并 說 明 理 由；（2）在 圖5 中，如 果DA=DE，試猜想CF與FE′有何關系，并進行 證 明；（3）在 圖4 中，如 果AB=15 ，CF=3，請直接寫出線段DE的長.

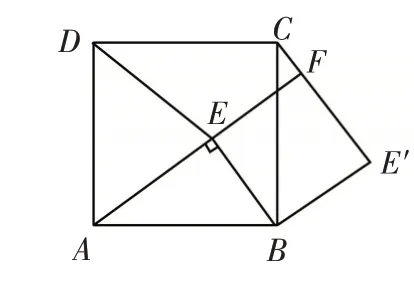
圖4

圖5

作為前三道例題的變式，本題在設問方式上較為新穎，第（1）問以判斷并說明理由的方式呈現，突出了學生在解答上要體現出數學問題的邏輯層次感，先判斷后說明，說明也即是通過說理來證實之前對問題的判斷，考查了學生的數感與邏輯思維.第（2）問如法炮制，讓學生先猜想后證明，猜想與判斷相似，證明則有說理的味道，但是兩者不能等同，證明就是通過數學推理來說明對線段關系的猜想結論的正確性，對學生數學語言的表達要求更為嚴謹，尤其體現了對學生數學核心素養之邏輯推理能力的考查.第（3）問則直接寫出線段的長度，無需證明與推理，解答難度比第（1）（2）問較低，體現了在變式問題的設置上的，讓不同水平的學生都能夠進行作答，讓不同層次的學生都能夠有所收獲的命題理念.

分析與解答：（1）通過判斷知，四邊形BE′FE是正方形，理由如下：由于把直角△ABE沿順時針方向繞點B旋轉90°后到達△CBE′的位置，所以∠AEB=∠CE′B=90°，BE=BE′，∠EBE′=90°，又因為∠BEF=90°，所以四邊形BE′FE是矩形，同時又因為BE=BE′，故四邊形BE′FE是正方形.

（2）通過猜想知CF=E′F；如圖6，作DH⊥AE并 交 于 于 點H，因 為DA=DE，DH⊥AE,所以AH=AE，DH⊥AE, 所以∠ADH+∠DAH=90°，又因為四邊形ABCD是正方形，得到AD=AB,∠DAB=90° ，于 是∠ADH+∠EAB= 90° ，所 以∠ADH=∠EAB∠EAB，又因為AD=AB，∠AHD=∠AEB=90°，于是△ADH≌△BAE，所以AH=BE=AE，由于把直角△ABE沿順時針方向繞點B旋轉90°后到達△CBE′的位置，所以AE=CE′，同時由于四邊形BE′FE是 正 方 形，所 以BE=E′F，故E′F=CE′，即CF=E′F.

圖6

（3）如圖7，作DH⊥AE并 交 于點H，由于四邊形BE′FE是正方形，所以BE′=E′F=BE，又AB=BC=15 ，CF=3，BC2=E′B2+E′C2，于是225=E′B2+(E′B+3)2，所 以E′B=9=BE，即CE′=CF+E′F=12 . 通 過（2）的 求 解 可得：BE=AH=9 ，DH=AE=CE′=12 ，所以HE=3，故DE===3.

圖7

3 理解旋轉，提升素養

旋轉讓靜態的圖形有了動態感，更能夠考查學生對圖形在運動狀態下的變化規律的理解與把握.在本文中，四道例題的解決都是以正方形為基本圖形，借助旋轉的圖形的性質來完成，在設問方式上，四道例題從求邊、角到三角形的全等，難度層層遞進，拾級而上，體現了通過變式教學來完成對基礎知識、基本概念的考查特點；在問題的解決中，突出了對學生運算能力與邏輯推理能力的滲透，以期達到提升學生數學素養的目的.